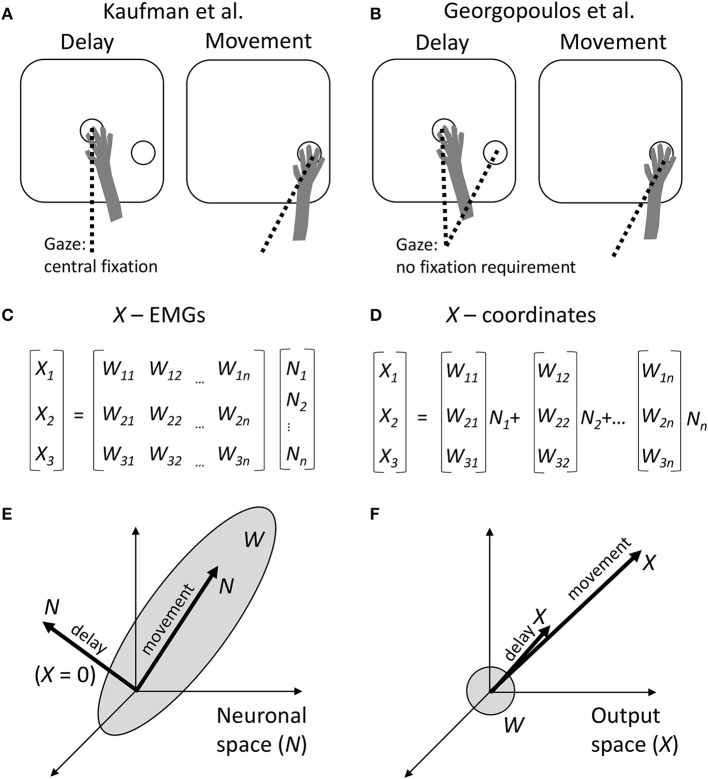
Figure 1.

Comparison between the approaches of Kaufman et al. and Georgopoulos et al. (A) Schematics of the experimental task of Kaufman et al. During the delay period, a monkey held the arm at the central position and was required to fixate that position with the eyes. The target of movement was visible, but the monkey had to withhold arm and eye movements. After the central fixation point disappeared, the monkey reached toward the target and was allowed to break eye fixation. (B) Experimental task of Georgopoulos et al. The task did not constrain eye movements. Possibly, during the delay the monkeys fixated either the central location or the target, and during the movement they fixated the target. (C) Conversion of neuronal activity into the outputs by Kaufman et al. A linear transformation W is applied to neuronal rates N to produce the outputs X. (D) Georgopoulos' population-vector approach. Although the same type of linear transformation is used, it is expressed somewhat differently as a sum of neuronal vectors [W_1i W_2i W_3i] weighted by neuronal rates N_i. (E) The result of Kaufman et al. The transformation W defines a subspace in the neuronal space, called output-potent space. During the movement period, neuronal population activity N resides in this subspace. However, during the delay, N resides in the null space, so X is close to zero. (F) Georgopoulos' result. The neuronal vectors point in various directions in the output space, defining roughly a sphere. The population vector points in the direction of movement during both the movement period and delay period of the task. This disagrees with Kaufman's zero output during the delay.