Combining large number of weak biomarkers based on AUC

Abstract

Combining multiple biomarkers to improve diagnosis and/or prognosis accuracy is a common practice in clinical medicine. Both parametric and non-parametric methods have been developed for finding the optimal linear combination of biomarkers to maximize the area under the receiver operating characteristic curve (AUC), primarily focusing on the setting with a small number of well-defined biomarkers. This problem becomes more challenging when the number of observations is not order of magnitude greater than the number of variables, especially when the involved biomarkers are relatively weak. Such settings are not uncommon in certain applied fields. The first aim of this paper is to empirically evaluate the performance of existing linear combination methods under such settings. The second aim is to propose a new combination method, namely, the pairwise approach, to maximize AUC. Our simulation studies demonstrated that the performance of several existing methods can become unsatisfactory as the number of markers becomes large, while the newly proposed pairwise method performs reasonably well. Furthermore, we apply all the combination methods to real datasets used for the development and validation of MammaPrint. The implication of our study for the design of optimal linear combination methods is discussed.

1. Introduction

The receiver operating characteristic (ROC) curve is a very useful tool in diagnostics/prognostics for the purpose of evaluating the discriminatory ability of biomarkers or diagnostic/prognostic tests. For a continuous-scaled marker, the ROC curve graphically depicts the marker’s diagnostic/prognostic ability for all threshold values in a unit square by plotting proportion of true positives (sensitivity) versus proportion of false positives (1− specificity). Extensive statistical research has been carried out in this field [1–5]. For excellent reviews of statistical methods involving ROC curves, see [6,7] and [8]. The area under the ROC curve (AUC) is the most popular overall discrimination accuracy index, and it has been extensively used by many researchers for biomarker evaluation and selection. Greater AUC value indicates greater discriminatory ability of a diagnostic/prognostic test or biomarker over all threshold values.

In clinical medical practices, single biomarker may not possess desired sensitivity and/or specificity for disease classification and outcome prediction. Multiple biomarkers are often combined in a linear fashion to form a single more powerful composite score that achieves better diagnostic/prognostic accuracy. An optimal linear combination of biomarkers is defined as the one for which the composite score would achieve the maximum AUC over all possible linear combinations. A number of parametric or nonparametric methods had been described in literature to find the optimal linear combination to maximize the AUC [9–12]. These methods generally only target the settings with a small number (up to five) of well-defined clinical biomarkers (AUC > 0.7). The performance of these methods for large number of biomarkers has not been explored.

For diagnostic/prognostic assay developed from the new generation of biotechniques, we often encounter the scenarios with large number of relatively weak biomarkers (0.5 < AUC < 0.7). More details can be found in Section 2, which presents some details of MammaPrint^®, an Food and Drug Administration-approved breast cancer prognostic test. Given the rapid development of personalized medicine where new diagnostic/prognostic tests developed under such setting are becoming increasingly common, combining large number of weak biomarkers to achieve the best possible diagnostic accuracy is of paramount importance in practice. Therefore, in this article, we not only empirically evaluated and investigated the performance of the existing linear combination methods but also presented a new method, namely, the pairwise approach, specifically targeting the setting described earlier.

The rest of the paper is organized as follows. In Section 2, MammaPrint^® is illustrated. In Sections 3.1 and 3.2, notations and brief review of existing methods are presented. Section 3.3 presents the newly proposed pairwise combination method. In Section 3.4, the approach of independent validation is discussed. Simulation studies to comprehensively evaluate and investigate the performance of the methods discussed are given in Section 4. In Section 5, application of the illustrative example is presented. Section 6 contains a summary and discussion.

2. A motivating example

Breast cancer is the second leading cause of cancer deaths in women in the USA, with approximately 39,620 US women expected to die from breast cancer in 2013. MammaPrint^® is the first Food and Drug Administration-cleared prognostic test for breast cancer. It combines the expression levels of 70 genes to provide patient binary prediction of likelihood of distant recurrence in the first 5 years following diagnosis [13,14]. A recent report from the Institute of Medicine showed that MammaPrint^® test has been used in 14,000 patients as of mid-2011 [15].

MammaPrint^® represents an illustrative example of the setting for which we will focus in this study. First, unlike the conventional setting where only a few (usually 2–4) markers are combined, it consists of 70 markers. Second, the number of samples used to establish MammaPrint^® is 78, and the number of samples for independent validation of MammaPrint^® ranges from 84 to 307 [16–19]. Third, most of the 70 markers involved have relatively weak discriminatory ability. As shown in Figure 1a, the AUCs of the 70 markers havev the maximum value of 0.694 (95% CI: 0.634–0.753 estimated by bootstrapping), and the median of 0.581 (mean 0.583), with most of them in the range of 0.50–0.65, based on the 463 samples pooled from different studies [16–19]. A closer look reveals that for 29 of the 70 biomarkers (41%), the AUCs are not significantly larger than 0.5 based on the 95% CI calculated by bootstrapping. In addition, the overall correlation among the markers involved are relatively weak. As shown in Figure 1b, the estimated size (absolute value) of correlation coefficient among the 70 markers ranges from 0 to 0.768, with a median of 0.128 (mean 0.161).

Figure 1.

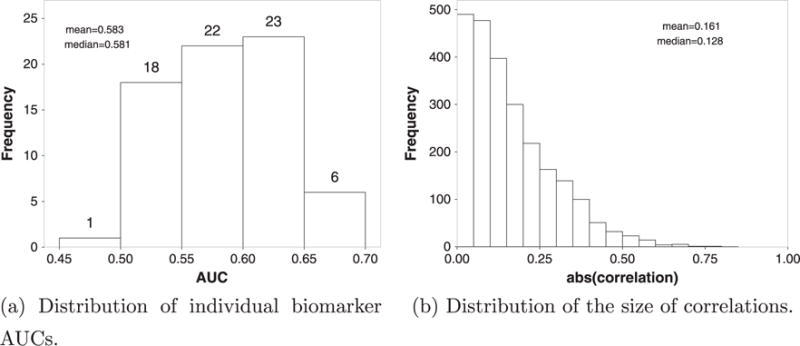
Characteristics of MammaPrint^® test dataset. AUC, area under the receiver operating characteristic curve.

While a number of methods had been described in literature [9–12] to find the optimal linear combination of markers in order to maximize the AUC, generally they are not developed and evaluated for the setting illustrated by MammaPrint^®. Therefore, the goal of this work is to investigate the performance of existing linear combination methods as well as a newly proposed one, namely, the pairwise approach, for yielding the maximum AUC under such setting.

3. Preliminaries

3.1. Notations

Consider the scenario where n patient was classified to two groups (g = 0, 1) of healthy (y_0i = 0; i = 1, …, n₀) and diseased (y_1j = 1; j = 1, …, n₁). With p continuous biomarkers x, let x_0i = (x_0i1, …, x_0ip)^T and x_1j = (x_1j1, …, x_1jp)^T represent the measurements of the different groups, where x_0ik and x_1jk are the k^th (k = 1, …, p) biomarker’s value for the i^th (i = 1, …, n₀) healthy and j^th (j = 1, …, n₁) diseased subject, respectively. Note that the biomarkers may have different distributions in the healthy and diseased groups. The n₀ × p matrix ${\mathit{X}}_0={({\mathit{x}}_{01},{\mathit{x}}_{02},\dots ,{\mathit{x}}_{0n_1})}^T$ and the n₁ × p matrix ${\mathit{X}}_1={({\mathit{x}}_{11},{\mathit{x}}_{12},\dots ,{\mathit{x}}_{1n_1})}^T$ represent the observed measurements for the healthy and diseased group, respectively.

A linearly combined biomarker could be created in the form of z = λx, where λ = (λ₁, λ₂, …, λ_p) is the combination coefficients, that is, risk coefficients. We denote z₀ and z₁ as the calculated vectors of the combined marker for the healthy and diseased groups, respectively:

$${\mathit{z}}_g=\mathit{\lambda }{\mathit{X}}_g^T\text{for}g=0,1.$$ (1)

It is worth pointing out that the optimal combinations are not unique, as applying scalar multiplier could produce equivalence results.

3.2. The existing methods

3.2.1. Parametric methods

Su and Liu’s method based on multinormality assumption

Assume biomarkers in both healthy and diseased population follow multivariate normal distributions, that is, x₀ ∼ N_p(μ₀, Σ₀) and x₁ ∼ N_p(μ₁, Σ₁), respectively. The classification problems under such assumption had been studied early on [20], and the result was extended by Su and Liu [9], who showed that the risk coefficients of the optimal linear combinations that yield largest AUC to be the Fisher’s discriminant coefficients:

$${\mathit{\lambda }}^T={({\sum }_1+{\sum }_0)}^{-1}\mu ,$$ (2)

where μ = μ₁ − μ₀. Subsequently the optimal combined AUC is

$$\mathit{AUC}=\mathrm{\Phi }\left(\sqrt{{\mu }^T{({\sum }_1+{\sum }_0)}^{-1}\mu }\right).$$ (3)

Su and Liu [9] had shown that the AUC is maximized among all possible linear combinations under the multinormality assumption, and the sample means and sample covariance matrices can be used to consistently estimate the aforementioned parameters.

The applicability of Su and Liu’s method is restricted by the normality assumption. Furthermore, the estimation of population parameters become unstable when the number of biomarkers becomes close to sample size [21–23]. It is also worth to point out that as the number of markers increases, the estimated sample covariance matrices may be less than full rank. The Moore–Penrose generalized inverse of the matrices was then used.

Logistic regression method

The logistic regression yields a linear combination of markers that intuitively discriminates non-diseased subjects from the diseased. To be specific,

$$\mathit{logit}(P[Y_i=1|x_i])=\mathit{\beta }{\mathit{x}}_{\mathit{i}}={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip};i=1,\dots n,$$ (4)

where x_i is the p-dim vector of biomarker measurements for the i-th patient, and Y_i being the disease status, 1 for diseased and 0 for healthy. The logistic regression coefficients $\widehat{\mathit{\beta }}$ can be used as the maximum likelihood estimation of the model, which yields an intuitively appealing quantity for discriminating the two groups [24–26]. The risk coefficients can be calculated based on $\widehat{\mathit{\beta }}$:

$$\mathit{\lambda }=(1,{\beta }_2/{\beta }_1,\cdots {\beta }_p/{\beta }_1).$$ (5)

Of course, the vector coefficient $\widehat{\mathit{\beta }}$ is chosen to maximize the logistic likelihood function rather than to maximize the AUC.

Regularized logistic regression: ridge and LASSO

Regularization methods have been used to prevent overfitting when large number of covariates are presented in the model. By imposing a penalty on the size of regression parameters, smaller prediction errors for new data might be achieved by reducing the overfitting through the bias–variance tradeoff [27]. The most common variants in regression are L₁ and L₂ regularization, usually refer to as LASSO (Least Absolute Shrinkage and Selection Operator) [28] and ridge regression [29], respectively. They are very similar to least squares regression except that the addition of predictors were penalized with L₁ or L₂ norm of the parameter vector. For example, in the linear model, the ridge regression coefficient estimates are

$${\widehat{\mathit{\beta }}}^{\mathit{R}}=\underset{\mathit{\beta }}{\arg min}{(\mathit{y}-\mathit{X}\mathit{\beta })}^T(\mathit{y}-\mathit{X}\mathit{\beta })+\mathit{\beta }{\mathit{\beta }}^T\mathit{\beta },$$ (6)

and the LASSO coefficient estimates are

$${\widehat{\mathit{\beta }}}^{\mathit{L}}=\underset{\mathit{\beta }}{\arg min}{(\mathit{y}-\mathit{X}\mathit{\beta })}^T(\mathit{y}-\mathit{X}\mathit{\beta })+\mathit{\beta }{\displaystyle \sum _j|{\mathit{\beta }}_j|},$$ (7)

where α ⩾ 0 is a tuning parameter that controls the amount of regularization and the size of the coefficients. The increase of α will shrink the coefficients closer to each other and to zero. In practice, it is usually determined by cross-validation. Of these two methods, ridge regression shrinks coefficients more smoothly, while LASSO may reduce some of them to exact zero and result in variable selection. The linear models can be extended to binary-dependent variables through logistic transformation as logistic ridge regression [30] and logistic LASSO regression [31], which will be used in this study. The risk coefficients will be calculated in the same way as described in the previous section of logistic regression method.

3.2.2. Non-parametric methods

Without normality assumptions, empirical AUC has been proposed as an alternative non-parametric objective function by Pepe and Thompson [10]. It is equivalent to obtain risk coefficients by maximizing Mann–Whitney statistics:

$$\underset{\mathit{\lambda }}{\arg max}W(\mathit{\lambda })=\frac{1}{n_0{n}_1}{\displaystyle \sum _{i=1}^{n_0}{\displaystyle \sum _{j=1}^{n_1}I({\lambda }_1{x}_{1j1}+\cdots +{\lambda }_p{x}_{1jp}>{\lambda }_1{x}_{0i1}+\cdots +{\lambda }_p{x}_{0ip})}},$$ (8)

where I is the indicator function. Without any assumptions about the distributions of x₀ and x₁, this non-parametric method is robust against distribution assumptions and had been shown to be superior than parametric approaches in some settings. Closely related to rank statistics, it had been recognized as a special case of the maximum rank correlation estimator [32] and had been shown to be consistent and asymptotically normal if at least one component of x is continuous and logit(P[y = 1|x]) follows a generalized linear model [33].

One limitation embedded in this method is related to its computational complexity as usually a search algorithm must be used [10]. With larger number of biomarkers involved, this empirical optimization process becomes computationally formidable, which calls for the development of methods with efficient search reduction strategies to make the search computationally tractable [24,34].

Min–max method

Liu et al. [11] proposed a non-parametric approach that linearly combines the minimum and maximum values of the observed biomarkers of each subjects. That is, they optimized the Mann–Whitney statistics:

$$\underset{\mathit{\lambda }}{\arg max}W(\mathit{\lambda })=\frac{1}{n_0{n}_1}{\displaystyle \sum _{i=1}^{n_0}{\displaystyle \sum _{j=1}^{n_1}I(x_{1j,\mathit{max}}+\lambda x_{1j,\mathit{min}}>x_{0i,\mathit{max}}+\lambda x_{0i,\mathit{min}})}},$$ (9)

where for the ith healthy subject

$$x_{0i,\mathit{max}}=\underset{1\le l\le p}{max}{x}_{0il},x_{0i,\mathit{min}}=\underset{1\le l\le p}{min}{x}_{0il},$$ (10)

and for the jth diseased subject

$$x_{1j,\mathit{max}}=\underset{1\le l\le p}{max}{x}_{1jl},x_{1j,\mathit{min}}=\underset{1\le l\le p}{min}{x}_{1jl}.$$ (11)

Only one risk coefficient is needed in this method, so the computational complexity is only related to the sample size, regardless of the number of biomarkers involved. They had shown that the maximum (minimum) levels yield larger sensitivity (specificity) than any individual biomarker, may yield larger partial or full AUC in certain scenarios, and is more robust against distributional assumptions.

However, as pointed out by the author, the feasibility might be an issue when not all biomarkers are measured on the same scale and are comparable.

Stepwise method

To side-step some of the drawbacks observed in min–max method, a different nonparametric algorithm to lower the computational complexity was implemented by Kang et al. [12], combining biomarkers using a stepwise fashion. The algorithm can be summarized as follows:

1. Calculate empirical AUC (or the Mann–Whitney statistics) of each biomarker.

2. Order the empirical AUC, from largest to smallest.

3. Combine the first two biomarkers using the method suggested by Pepe and Thompson [10].

4. Create a combined marker based on risk coefficients in the aforementioned step, combine it with the next biomarker.

5. Follow the aforementioned two steps until all biomarkers were included.

The procedure was referred to as ‘step-down’ combination method as it combines biomarkers ‘downward’ in the aforementioned step 2. It may also be desirable to combine the biomarkers ‘upward’ by sorting them from smallest to largest in step 2, for a ‘step-up’ combination method. It had been argued that any other stepwise approach selecting different preceding order would perform somewhere in between [35]. It had been demonstrated that this non-parametric method may outperform other methods under some scenarios and can be extended to three ordinal categories [12,34].

These existing methods generally focus on the combination of a few well-defined clinical markers. The applicability of the these methods has not been investigated systematically for the scenarios with large number of weak markers.

3.3. The proposed method

Targeting the settings with large number of weak markers, we propose a new non-parametric method to estimate the combination coefficients by pairing one marker with the rest separately, hereafter referred to as ‘pairwise’ methods. Given the fact that majority of involved markers are weak in our setting, it is important to focus on one marker that contributes the most information to classification. Preferably, this marker is chosen based on clinical verification. We refer this marker as ‘anchor marker’ hereafter. When clinical justification is not available, the one with the largest AUC can be used as the anchor marker. Most likely, given the anchor marker, any additional contribution from other markers highly depends on their correlation with the anchor markers, while the relationships among them play a secondary role. For demonstration purposes, we use the marker with the largest AUC as anchor marker in this paper.

We use empirical AUC as objective function and the grid search [10] as optimization method. The implementation of the algorithm can be summarized as follows:

1. Calculate empirical AUC of each marker.

2. Choose the one with largest empirical AUC as the anchor marker M₍₁₎.

3. Combine the kth biomarkers M_k with the anchor biomarker M₍₁₎, and estimate the combination coefficients with grid search method using empirical AUC as objective function. That is, to find the maximum in:

   $$W\left({\lambda }_k^{(1)},{\lambda }_k\right)=\frac{1}{n_0{n}_1}{\displaystyle \sum _{i=1}^{n_0}{\displaystyle \sum _{j=1}^{n_1}I\left({\lambda }_k^{(1)}{x}_{1j(1)}+{\lambda }_k{x}_{1jk}>{\lambda }_k^{(1)}{x}_{0i(1)}+{\lambda }_k{x}_{0ik}\right),}}$$

   where combination coefficients ${\lambda }_k^{(1)}$, λ_k will take equally spaced values (201 steps each by default) in two-dimensional grid space bounded by [−1, 1], similar to that used in [10] and [12]. This will produce a wide range of standardized combination coefficients for the next step.
4. Standardize the combination coefficients against the anchor marker:

   $${\lambda }_k^{\ast }={\lambda }_k/{\lambda }_k^{(1)}.$$
5. The overall linear combination coefficients are obtained by combining the linear combination coefficients obtained in the previous step:

   $$\mathit{\lambda }=\pm 1\ast \left({\lambda }_1^{\ast },\dots ,{\lambda }_{(1)}=1,\dots ,{\lambda }_k^{\ast },\dots ,{\lambda }_p^{\ast }\right),$$ (12)

   where we choose λ₍₁₎ = 1 if the median of the combined marker in the diseased population is larger than that of the healthy one, otherwise, −1 for identifiability.

This new pairwise approach has several advantages. First, it is distribution-free and therefore more robust than parametric methods. Second, it tries to utilize all available markers regardless of marginal marker performance. As pointed out by some researchers [36], even extremely weak markers may enhance the performance of combination in certain circumstances. Third, when the number of observations is not order of magnitude greater than the number of variables, as illustrated in our motivating example, over-fitting and multicollinearity can severely impact the consistency and stability of combination coefficient estimation [21,22]. Unlike the stepwise method that employs iterative fitting of combination coefficients in the training dataset, the pairwise method estimates each coefficients in a single optimization step, and thus it offers a relief from the potential overfitting risk in the empirical search of combination coefficients. Fourth, it greatly reduces computational complexity, making the non-parametric grid search method feasible for cases with more than a handful markers. In addition, the framework of the proposed approach is flexible and expandable. For example, the objective function in step 3 is not limited to the empirical AUC. Other quantities, such as accuracy or Youden index, can be used depending on the need. The maximizing procedure can be also adapted to other parametric or non-parametric methods, such as logistic regression, depending on the nature of the markers.

3.4. Independent validation

Accurate estimation of the performances is essential for comparing the aforementioned methods. Usually, re-substitution method was used as presented in some of the existing methods [9–11,24]. In such process, the linear combination coefficients were first estimated, and the composite scores for each sample were calculated using the estimated coefficients on the same dataset. The AUCs were then estimated based on the combined scores, and superiority of a certain method was concluded if the associated AUC is the largest. However, the estimated AUC by re-substitution method was usually over optimistic for future observations, as pointed out by many researchers [12, 37–39]. This is the well-known effect of ‘testing hypotheses suggested by the data’ [40].

Cross-validation is a widely used method to adjust such upward bias from the estimation by re-substitution. By partitioning a given dataset into ‘training’ and ‘testing’ datasets for separate estimation and validation, the upward bias might be statistically controlled. Commonly used methods include K-fold cross-validation, leave-one-out cross-validation (Jack-knife), repeated random sub-sampling validation, and others [39,41–43].

In clinical practice, independent validation is the key and most stringent standard for marker performance evaluation, where the ‘training’ and ‘testing’ datasets are obtained independently. The aforementioned cross-validation is only necessary when the validation dataset is not available, and thus one dataset must be used in both estimation and evaluation by re-sampling techniques [44]. To achieve the same stringency standard in our simulation, a dataset was first generated (‘training’ dataset) and based on which the linear combination coefficients were derived for each methods. The coefficients were then applied to a dataset independently generated with the same parameters (‘testing’ dataset) to create composite scores by different methods. The performances of the different combination methods were then compared based on the empirical AUCs calculated from the composite scores in this independently generated test set.

4. Simulation study

This section contains two parts: (1) comparing the performances of the aforementioned combination methods under different marginal distribution and covariance structure, presented in Section 4.1; and (2) investigating the bias in estimating AUC and overfitting issues in the combination methods, presented in Section 4.2.

4.1. Comparison of the performance of different combination methods

We performed simulation studies to assess the performance of the aforementioned combination methods, that is, Su and Liu’s multivariate normal based on Fisher’s linear discriminant (MVN) [9], logistic regression (LR) [10], non-parametric min–max (MM) [11], non-parametric stepwise with downward direction (SW) [34], two regularized regression methods (logistic ridge [30] and LASSO [28, 31]), and the newly proposed non-parametric pairwise using grid search method (PW).

Extensive simulations were carried out, with a wide range of joint distributions and effect sizes of markers: (1) multivariate normal distributions with equal and unequal covariance, where one marker possesses moderate discriminatory ability (marginal AUC = 0.738), and the others are weaker (marginal AUC = 0.611); (2) multivariate normal distributions with equal and unequal covariance, where the markers are characterized by weak discriminatory ability (marginal AUCs range evenly from 0.528 to 0.664); (3) multivariate gamma distributions with equal and unequal covariance, and the effect sizes of markers are the same as scenario 2; and (4) multivariate beta distributions with equal and unequal covariance, and the effect sizes of markers are the same as scenario 2. We choose markers with moderate-to-weak discriminatory ability in order to simulate the targeted settings as illustrated by MammaPrint (Section 2). In all settings, we considered sample sizes of (n₀, n₁) = (25, 25), (100, 100) for healthy and diseased groups. For each setting, two independent sets, that is, one as ‘training set’ and another the ‘testing set’, of observations were generated from the same underlying distribution with given parameter set and sample size. Each combination method was applied to the training set, and the estimated combination coefficients (λ) were obtained. The combination coefficients λ are then applied to the independently simulated testing set from the same underlying joint distribution to obtain the combined markers, of which the ROCs and AUCs will be calculated. The AUC for each combination method is estimated by the mean of AUC over the 1000 simulations, and its 95% CIs by the 2.5 and 97.5 quantiles. The results were summarized in Tables I–IV.

Table I.

Estimated AUC and its 95% confidence intervals. Multivariate normal distributions: μ₀ = 0, μ₁ = (0.4, ⋯, 0.9)^T.

		Mean AUC							Confidence interval
(n0, n1)	p	PW	SW	MM	MVN	LR	Ridge	LASSO	PW	SW	MM	MVN	LR	Ridge	LASSO
Σ0 = Σ1 = 0.85Ip×p + 0.15Jp×p (equal covariance in diseased and healthy groups)
(25,25)	2	0.7303	0.7303	0.7102	0.7356	0.7355	0.7371	0.7286	(0.584, 0.864)	(0.584, 0.864)	(0.525, 0.859)	(0.592, 0.866)	(0.595, 0.864)	(0.597, 0.867)	(0.500, 0.864)
	4	0.7253	0.7216	0.7040	0.7278	0.7277	0.7357	0.7219	(0.555, 0.874)	(0.546, 0.866)	(0.534, 0.842)	(0.568, 0.874)	(0.570, 0.872)	(0.587, 0.874)	(0.500, 0.866)
	6	0.7208	0.7124	0.7018	0.7167	0.7157	0.7337	0.7167	(0.531, 0.864)	(0.534, 0.864)	(0.521, 0.845)	(0.549, 0.859)	(0.549, 0.858)	(0.586, 0.866)	(0.500, 0.862)
	10	0.7172	0.6921	0.6941	0.6897	0.6876	0.7262	0.7034	(0.541, 0.858)	(0.515, 0.845)	(0.520, 0.837)	(0.485, 0.840)	(0.506, 0.840)	(0.574, 0.866)	(0.500, 0.854)
	20	0.7279	0.6777	0.6998	0.6590	0.6394	0.7352	0.7043	(0.552, 0.862)	(0.496, 0.834)	(0.522, 0.842)	(0.486, 0.822)	(0.454, 0.810)	(0.568, 0.866)	(0.500, 0.856)
	50	0.7353	0.6440	0.7045	0.5720	0.5676	0.7418	0.6917	(0.550, 0.870)	(0.475, 0.805)	(0.541, 0.837)	(0.446, 0.725)	(0.458, 0.702)	(0.587, 0.866)	(0.500, 0.854)
(100,100)	2	0.7449	0.7449	0.7263	0.7454	0.7455	0.7456	0.7451	(0.675, 0.810)	(0.675, 0.810)	(0.651, 0.795)	(0.676, 0.810)	(0.676, 0.810)	(0.677, 0.810)
											(0.677, 0.810)
	4	0.7502	0.7481	0.7178	0.7502	0.7501	0.7509	0.7498	(0.677, 0.813)	(0.671, 0.812)	(0.640, 0.786)	(0.678, 0.814)	(0.678, 0.815)	(0.678, 0.815)	(0.678, 0.812)
	6	0.7536	0.7485	0.7148	0.7517	0.7517	0.7536	0.7530	(0.680, 0.822)	(0.669, 0.821)	(0.643, 0.785)	(0.677, 0.821)	(0.677, 0.820)	(0.677, 0.822)	(0.679, 0.821)
	10	0.7572	0.7460	0.7138	0.7498	0.7496	0.7553	0.7546	(0.684, 0.824)	(0.673, 0.811)	(0.640, 0.782)	(0.678, 0.816)	(0.678, 0.815)	(0.685, 0.821)	(0.686, 0.820)
	20	0.7660	0.7400	0.7169	0.7431	0.7424	0.7616	0.7617	(0.695, 0.830)	(0.659, 0.813)	(0.641, 0.783)	(0.664, 0.814)	(0.662, 0.814)	(0.687, 0.827)	(0.685, 0.824)
	50	0.7658	0.7085	0.7174	0.7003	0.6961	0.7600	0.7605	(0.702, 0.826)	(0.621, 0.783)	(0.645, 0.783)	(0.614, 0.774)	(0.612, 0.772)	(0.695, 0.822)	(0.691, 0.824)
	100	0.7656	0.6880	0.7205	0.6415	0.6155	0.7603	0.7603	(0.696, 0.825)	(0.606, 0.761)	(0.646, 0.785)	(0.548, 0.723)	(0.525, 0.703)	(0.692, 0.822)	(0.690, 0.824)
	150	0.7677	0.6831	0.7244	0.5881	0.5749	0.7622	0.7613	(0.706, 0.831)	(0.600, 0.764)	(0.651, 0.790)	(0.489, 0.682)	(0.481, 0.665)	(0.694, 0.823)	(0.690, 0.830)
	200	0.7684	0.6818	0.7264	0.5370	0.5327	0.7630	0.7615	(0.700, 0.830)	(0.593, 0.766)	(0.654, 0.791)	(0.473, 0.619)	(0.477, 0.599)	(0.687, 0.825)	(0.691, 0.829)
Σ0 = 0.9Ip×p + 0.1Jp×p and Σ1 = 0.85Ip×p + 0.15Jp×p (Unequal covariance)
(25,25)	2	0.7321	0.7321	0.7123	0.7371	0.7370	0.7385	0.7308	(0.587, 0.864)	(0.587, 0.864)	(0.536, 0.854)	(0.597, 0.867)	(0.595, 0.866)	(0.597, 0.867)	(0.500, 0.866)
	4	0.7239	0.7194	0.7048	0.7262	0.7260	0.7339	0.7209	(0.541, 0.861)	(0.536, 0.858)	(0.523, 0.850)	(0.554, 0.864)	(0.557, 0.866)	(0.579, 0.866)	(0.500, 0.867)
	6	0.7295	0.7204	0.7088	0.7248	0.7234	0.7397	0.7211	(0.566, 0.871)	(0.544, 0.867)	(0.536, 0.851)	(0.546, 0.870)	(0.533, 0.869)	(0.570, 0.877)	(0.500, 0.872)
	10	0.7248	0.7013	0.7020	0.7022	0.7003	0.7368	0.7082	(0.550, 0.867)	(0.518, 0.850)	(0.525, 0.842)	(0.518, 0.858)	(0.517, 0.856)	(0.592, 0.872)	(0.500, 0.861)
	20	0.7432	0.6858	0.7106	0.6706	0.6535	0.7470	0.7137	(0.587, 0.874)	(0.475, 0.846)	(0.552, 0.846)	(0.494, 0.823)	(0.478, 0.806)	(0.594, 0.870)	(0.500, 0.861)
	50	0.7516	0.6519	0.7228	0.5725	0.5666	0.7564	0.7063	(0.586, 0.883)	(0.477, 0.810)	(0.565, 0.854)	(0.448, 0.712)	(0.458, 0.693)	(0.619, 0.878)	(0.500, 0.859)
(100,100)	2	0.7464	0.7464	0.7279	0.7470	0.7470	0.7471	0.7466	(0.676, 0.812)	(0.676, 0.812)	(0.653, 0.796)	(0.678, 0.811)	(0.678, 0.811)	(0.678, 0.811)	(0.678, 0.812)
	4	0.7533	0.7514	0.7209	0.7534	0.7534	0.7541	0.7528	(0.681, 0.819)	(0.679, 0.818)	(0.639, 0.787)	(0.681, 0.819)	(0.681, 0.819)	(0.680, 0.819)	(0.681, 0.818)
	6	0.7591	0.7542	0.7206	0.7570	0.7568	0.7587	0.7570	(0.682, 0.827)	(0.678, 0.826)	(0.642, 0.787)	(0.681, 0.827)	(0.681, 0.826)	(0.684, 0.828)	(0.685, 0.825)
	10	0.7664	0.7552	0.7204	0.7589	0.7587	0.7643	0.7615	(0.698, 0.829)	(0.683, 0.819)	(0.646, 0.783)	(0.687, 0.821)	(0.684, 0.822)	(0.696, 0.827)	(0.689, 0.825)
	20	0.7780	0.7521	0.7276	0.7549	0.7544	0.7733	0.7699	(0.709, 0.841)	(0.675, 0.822)	(0.654, 0.798)	(0.680, 0.829)	(0.678, 0.828)	(0.701, 0.842)	(0.702, 0.842)
	50	0.7824	0.7254	0.7329	0.7176	0.7127	0.7763	0.7721	(0.722, 0.839)	(0.642, 0.798)	(0.665, 0.799)	(0.636, 0.794)	(0.632, 0.785)	(0.710, 0.834)	(0.701, 0.834)
	100	0.7842	0.7015	0.7379	0.6550	0.6285	0.7775	0.7726	(0.714, 0.844)	(0.615, 0.781)	(0.668, 0.802)	(0.562, 0.734)	(0.536, 0.717)	(0.708, 0.836)	(0.702, 0.836)
	150	0.7868	0.6959	0.7440	0.5991	0.5857	0.7808	0.7737	(0.724, 0.847)	(0.603, 0.778)	(0.674, 0.809)	(0.502, 0.693)	(0.488, 0.673)	(0.714, 0.842)	(0.702, 0.837)
	200	0.7878	0.6942	0.7472	0.5388	0.5336	0.7818	0.7748	(0.722, 0.847)	(0.602, 0.779)	(0.677, 0.812)	(0.471, 0.618)	(0.473, 0.602)	(0.714, 0.841)	(0.699, 0.839)

AUC, area under the receiver operating characteristic curve; PW, pairwise; SW, stepwise; MM, min–max; MVN, multivariate normal; LR, logistic regression; LASSO, Least Absolute Shrinkage and Selection Operator.

(n₀, n₁), sample sizes in healthy/diseased groups.

p, the number of markers.

Table IV.

Estimated AUC and its 95% confidence intervals. Beta distribution α₀ = 0.4, β₀ = 0.6 for healthy population, and α₁ = (0.45, …, 0.6), β₁ = 1 − α₁ for diseased population.

		Mean AUC							Confidence interval
(n0, n1)	p	PW	SW	MM	MVN	LR	Ridge	LASSO	PW	SW	MM	MVN	LR	Ridge	LASSO
Copula Σ0 = Σ1 = 0.85Ip×p + 0.15Jp×p (equal covariance in diseased and healthy groups)
(25,25)	10	0.6761	0.6554	0.6760	0.6571	0.6548	0.6896	0.6482	(0.512, 0.826)	(0.477, 0.805)	(0.512, 0.818)	(0.478, 0.821)	(0.486, 0.819)	(0.502, 0.835)	(0.500, 0.808)
	20	0.7003	0.6561	0.6907	0.6506	0.6334	0.7161	0.6624	(0.499, 0.850)	(0.485, 0.827)	(0.523, 0.834)	(0.483, 0.808)	(0.467, 0.797)	(0.534, 0.854)	(0.488, 0.835)
	50	0.7329	0.6524	0.7233	0.5868	0.5730	0.7483	0.6864	(0.546, 0.874)	(0.485, 0.819)	(0.558, 0.853)	(0.458, 0.734)	(0.454, 0.726)	(0.594, 0.883)	(0.500, 0.850)
	100	0.7510	0.6413	0.7373	0.6800	0.5603	0.7735	0.6975	(0.571, 0.888)	(0.469, 0.806)	(0.581, 0.882)	(0.494, 0.827)	(0.453, 0.693)	(0.638, 0.886)	(0.500, 0.837)
	200	0.7747	0.6201	0.7561	0.7445	0.5586	0.7961	0.7105	(0.587, 0.892)	(0.466, 0.805)	(0.610, 0.893)	(0.587, 0.872)	(0.451, 0.684)	(0.667, 0.908)	(0.500, 0.854)
(100,100)	10	0.7173	0.7063	0.6864	0.7105	0.7103	0.7180	0.7117	(0.642, 0.788)	(0.626, 0.785)	(0.610, 0.762)	(0.632, 0.784)	(0.632, 0.785)	(0.644, 0.787)	(0.630, 0.784)
	20	0.7442	0.7204	0.7020	0.7289	0.7274	0.7450	0.7350	(0.674, 0.814)	(0.637, 0.798)	(0.624, 0.775)	(0.645, 0.800)	(0.643, 0.798)	(0.671, 0.811)	(0.656, 0.804)
	50	0.7728	0.7249	0.7285	0.7446	0.7332	0.7821	0.7616	(0.706, 0.832)	(0.638, 0.803)	(0.659, 0.791)	(0.662, 0.815)	(0.650, 0.809)	(0.710, 0.843)	(0.686, 0.828)
	100	0.7834	0.7202	0.7449	0.7348	0.6924	0.8116	0.7797	(0.718, 0.847)	(0.634, 0.806)	(0.672, 0.812)	(0.647, 0.808)	(0.600, 0.778)	(0.753, 0.869)	(0.707, 0.846)
	200	0.7916	0.7164	0.7606	0.5643	0.5431	0.8520	0.7978	(0.724, 0.851)	(0.629, 0.797)	(0.689, 0.823)	(0.480, 0.667)	(0.479, 0.632)	(0.796, 0.903)	(0.727, 0.859)
Copula Σ0 = 0.9Ip×p + 0.1Jp×p and Σ1 = 0.85Ip×p + 0.15Jp×p (unequal covariance)
(25,25)	10	0.6797	0.6594	0.6826	0.6629	0.6612	0.6959	0.6524	(0.499, 0.834)	(0.491, 0.816)	(0.515, 0.826)	(0.470, 0.826)	(0.483, 0.822)	(0.526, 0.842)	(0.500, 0.816)
	20	0.7096	0.6632	0.7030	0.6571	0.6382	0.7250	0.6704	(0.525, 0.858)	(0.483, 0.826)	(0.544, 0.845)	(0.480, 0.813)	(0.469, 0.798)	(0.561, 0.864)	(0.499, 0.837)
	50	0.7462	0.6617	0.7379	0.5889	0.5722	0.7597	0.6963	(0.573, 0.882)	(0.486, 0.824)	(0.586, 0.866)	(0.459, 0.744)	(0.453, 0.731)	(0.606, 0.890)	(0.500, 0.856)
	100	0.7678	0.6410	0.7519	0.6918	0.5638	0.7878	0.7081	(0.600, 0.894)	(0.472, 0.813)	(0.603, 0.882)	(0.502, 0.834)	(0.459, 0.699)	(0.656, 0.898)	(0.500, 0.850)
	200	0.7937	0.6183	0.7732	0.7607	0.5599	0.8104	0.7204	(0.643, 0.906)	(0.461, 0.795)	(0.622, 0.901)	(0.611, 0.885)	(0.459, 0.685)	(0.678, 0.917)	(0.500, 0.864)
(100,100)	10	0.7231	0.7133	0.6925	0.7171	0.7170	0.7242	0.7177	(0.649, 0.794)	(0.633, 0.787)	(0.614, 0.767)	(0.641, 0.790)	(0.640, 0.790)	(0.648, 0.793)	(0.638, 0.791)
	20	0.7542	0.7318	0.7136	0.7383	0.7368	0.7542	0.7441	(0.684, 0.820)	(0.650, 0.803)	(0.635, 0.789)	(0.658, 0.809)	(0.655, 0.807)	(0.684, 0.820)	(0.670, 0.814)
	50	0.7868	0.7408	0.7437	0.7535	0.7417	0.7928	0.7734	(0.719, 0.842)	(0.657, 0.817)	(0.673, 0.812)	(0.672, 0.823)	(0.658, 0.816)	(0.722, 0.852)	(0.701, 0.838)
	100	0.7988	0.7367	0.7623	0.7408	0.6980	0.8209	0.7912	(0.735, 0.860)	(0.648, 0.821)	(0.691, 0.826)	(0.650, 0.815)	(0.600, 0.780)	(0.763, 0.876)	(0.721, 0.857)
	200	0.8085	0.7337	0.7797	0.5663	0.5424	0.8580	0.8083	(0.744, 0.865)	(0.650, 0.813)	(0.717, 0.840)	(0.488, 0.657)	(0.475, 0.632)	(0.800, 0.907)	(0.739, 0.867)

AUC, area under the receiver operating characteristic curve; PW, pairwise; SW, stepwise; MM, min–max; MVN, multivariate normal; LR, logistic regression; LASSO, Least Absolute Shrinkage and Selection Operator.

(n₀, n₁), sample sizes in healthy/diseased groups.

p, the number of markers.

4.1.1. Multivariate normal distributions with one moderate and multiple weak markers

Without loss of generality, we assume diseased and healthy samples are from multivariate normal distributions with marginal mean vector μ₀ = (0, …, 0)^T for healthy group. We set the marginal mean vector of the markers for diseased group as μ₁ = (0.4, …, 0.9)^T with marginal variances of all markers as 1. Consequently, it represents multiple weak markers (marginal AUCs equal to 0.611) combining with a moderate one (marginal AUC equals to 0.738). The covariance in diseased and healthy populations were assumed to be with exchangeable correlation. In the cases of equal covariances, we assume: Σ₁ = Σ₀ = (1 − γ)I_p×p + γJ_p×p where I is the identity matrix and J is a matrix of all 1s. Correlation parameter γ is set to be 0.15, similar to the median value of the correlation size observed in Section 2. In the cases of unequal covariances, we assume the covariance in diseased population unchanged, with a different covariance Σ₀ = 0.9I_p×p + 0.1J_p×p in healthy population. The simulation results were listed in Table I.

In both equal and unequal covariance scenarios, we observe the following: first, when the number of markers are relatively small (p ∼ 2 − 6), the mean of estimated AUC and its CI are generally comparable for all combination methods; second, when the number of markers increases to the level that the sample size is no longer order of magnitude greater than the number of markers, the PW and Ridge methods perform comparably, where PW method produces slightly greater AUC means with larger sample size n₀ = n₁ = 100, and Ridge method is slightly better at smaller sample size n₀ = n₁ = 25. Although the estimated AUC means are similar to that from PW and Ridge methods, LASSO produces noticeably larger CIs at smaller sample size. MM and SW methods produce only slightly smaller AUC mean; third, when the number of markers continues to grow, there is noticeable decrease in the AUC means for MVN and LR methods. This observation of decreased performance will be further investigated in Section 4.2. There is also a drop of performance for SW method, although it is less obvious than that of MVN and LR methods. On the other hand, we do not observe such performance drop for PW, ridge, LASSO, and MM methods, with PW/ridge/LASSO performing consistently better than MM method.

4.1.2. Multivariate normal distributions with multiple weak markers

The simulation is similar to that in the previous section, except that we set the marginal mean vector of the markers for diseased group as μ₁ = (0.1, …, 0.6)^T with even spacing based on the number of such markers. Consequently, the marginal AUCs are all different and range from 0.528 to 0.664. The simulation results were listed in Table II. Overall, similar performances are observed as in the previous simulation, that is, PW, ridge, and LASSO produce larger AUCs than the rest when the number of markers increases. However, in this case, the ridge method tend to be universally better than PW and LASSO.

Table II.

Estimated AUC and its 95% confidence intervals. Multivariate normal distributions: μ₀ = 0, μ₁ = (0.1, ⋯, 0.6)^T evenly spaced.

		Mean AUC							Confidence interval
(n0, n1)	p	PW	SW	MM	MVN	LR	Ridge	LASSO	PW	SW	MM	MVN	LR	Ridge	LASSO
Σ0 = Σ1 = 0.85Ip×p + 0.15Jp×p (equal covariance in diseased and healthy groups)
(25,25)	2	0.6409	0.6409	0.6114	0.6453	0.6457	0.6458	0.6224	(0.470, 0.784)	(0.470, 0.784)	(0.469, 0.771)	(0.461, 0.795)	(0.470, 0.794)	(0.469, 0.794)	(0.490, 0.794)
	4	0.6504	0.6476	0.6329	0.6536	0.6533	0.6616	0.6290	(0.483, 0.810)	(0.470, 0.813)	(0.474, 0.782)	(0.482, 0.818)	(0.482, 0.818)	(0.478, 0.814)	(0.475, 0.811)
	6	0.6607	0.6506	0.6420	0.6558	0.6550	0.6739	0.6357	(0.481, 0.816)	(0.477, 0.808)	(0.472, 0.794)	(0.466, 0.818)	(0.466, 0.816)	(0.477, 0.827)	(0.488, 0.810)
	10	0.6686	0.6489	0.6440	0.6513	0.6494	0.6830	0.6387	(0.490, 0.827)	(0.470, 0.813)	(0.467, 0.798)	(0.469, 0.808)	(0.472, 0.808)	(0.499, 0.834)	(0.490, 0.808)
	20	0.7041	0.6605	0.6610	0.6549	0.6398	0.7160	0.6672	(0.533, 0.848)	(0.490, 0.824)	(0.478, 0.807)	(0.474, 0.822)	(0.467, 0.811)	(0.549, 0.859)	(0.488, 0.830)
	50	0.7339	0.6529	0.6698	0.5850	0.5740	0.7499	0.6829	(0.558, 0.870)	(0.469, 0.816)	(0.482, 0.814)	(0.454, 0.734)	(0.464, 0.715)	(0.608, 0.886)	(0.500, 0.851)
(100,100)	2	0.6605	0.6605	0.6236	0.6612	0.6612	0.6612	0.6624	(0.584, 0.733)	(0.584, 0.733)	(0.537, 0.704)	(0.585, 0.735)	(0.584, 0.735)	(0.584, 0.734)	(0.585, 0.734)
	4	0.6802	0.6790	0.6458	0.6814	0.6814	0.6826	0.6808	(0.601, 0.756)	(0.602, 0.760)	(0.558, 0.719)	(0.604, 0.755)	(0.604, 0.755)	(0.604, 0.758)	(0.600, 0.755)
	6	0.6954	0.6918	0.6550	0.6952	0.6952	0.6979	0.6952	(0.612, 0.767)	(0.606, 0.768)	(0.575, 0.736)	(0.615, 0.771)	(0.615, 0.771)	(0.618, 0.775)	(0.611, 0.770)
	10	0.7161	0.7064	0.6662	0.7112	0.7112	0.7176	0.7118	(0.642, 0.788)	(0.623, 0.782)	(0.588, 0.739)	(0.633, 0.784)	(0.634, 0.782)	(0.644, 0.788)	(0.633, 0.785)
	20	0.7477	0.7270	0.6797	0.7377	0.7367	0.7515	0.7422	(0.676, 0.812)	(0.641, 0.803)	(0.601, 0.747)	(0.658, 0.811)	(0.657, 0.810)	(0.673, 0.817)	(0.662, 0.810)
	50	0.7696	0.7310	0.6870	0.7617	0.7537	0.7930	0.7697	(0.706, 0.828)	(0.644, 0.806)	(0.615, 0.756)	(0.683, 0.830)	(0.674, 0.824)	(0.729, 0.851)	(0.698, 0.834)
	100	0.7799	0.7308	0.6933	0.7630	0.7232	0.8350	0.7963	(0.710, 0.847)	(0.637, 0.812)	(0.615, 0.765)	(0.681, 0.836)	(0.636, 0.800)	(0.771, 0.890)	(0.723, 0.858)
	150	0.7865	0.7293	0.6976	0.7168	0.6872	0.8627	0.8141	(0.718, 0.848)	(0.637, 0.810)	(0.622, 0.768)	(0.618, 0.809)	(0.585, 0.780)	(0.805, 0.914)	(0.740, 0.875)
	200	0.7893	0.7301	0.7004	0.5739	0.5466	0.8865	0.8263	(0.723, 0.854)	(0.636, 0.810)	(0.626, 0.765)	(0.478, 0.676)	(0.476, 0.637)	(0.831, 0.932)	(0.752, 0.887)
Σ0 = 0.9Ip×p + 0.1Jp×p and Σ1 = 0.85Ip×p + 0.15Jp×p (unequal covariance)
(25,25)	2	0.6421	0.6421	0.6119	0.6458	0.6460	0.6458	0.6231	(0.472, 0.790)	(0.472, 0.790)	(0.470, 0.776)	(0.470, 0.794)	(0.475, 0.794)	(0.464, 0.795)	(0.490, 0.792)
	4	0.6489	0.6476	0.6296	0.6500	0.6498	0.6586	0.6281	(0.466, 0.811)	(0.474, 0.806)	(0.474, 0.786)	(0.466, 0.806)	(0.467, 0.805)	(0.480, 0.811)	(0.461, 0.802)
	6	0.6668	0.6576	0.6443	0.6635	0.6632	0.6792	0.6410	(0.470, 0.827)	(0.483, 0.822)	(0.467, 0.794)	(0.486, 0.829)	(0.472, 0.829)	(0.504, 0.834)	(0.488, 0.827)
	10	0.6784	0.6587	0.6487	0.6620	0.6607	0.6913	0.6455	(0.488, 0.830)	(0.474, 0.818)	(0.470, 0.810)	(0.483, 0.827)	(0.501, 0.826)	(0.512, 0.838)	(0.490, 0.819)
	20	0.7127	0.6683	0.6677	0.6576	0.6413	0.7265	0.6752	(0.531, 0.853)	(0.481, 0.819)	(0.485, 0.811)	(0.467, 0.810)	(0.472, 0.803)	(0.571, 0.854)	(0.494, 0.834)
	50	0.7486	0.6602	0.6839	0.5865	0.5740	0.7606	0.6947	(0.581, 0.885)	(0.474, 0.829)	(0.504, 0.827)	(0.458, 0.746)	(0.461, 0.715)	(0.624, 0.882)	(0.500, 0.845)
(100,100)	2	0.6607	0.6607	0.6234	0.6614	0.6614	0.6614	0.6625	(0.583, 0.735)	(0.583, 0.735)	(0.535, 0.703)	(0.585, 0.735)	(0.585, 0.735)	(0.584, 0.735)	(0.585, 0.735)
	4	0.6828	0.6816	0.6474	0.6838	0.6838	0.6849	0.6826	(0.602, 0.756)	(0.600, 0.757)	(0.559, 0.723)	(0.601, 0.756)	(0.603, 0.755)	(0.605, 0.757)	(0.598, 0.756)
	6	0.7003	0.6967	0.6597	0.6993	0.6992	0.7017	0.6987	(0.621, 0.775)	(0.614, 0.772)	(0.578, 0.735)	(0.622, 0.775)	(0.622, 0.776)	(0.625, 0.778)	(0.621, 0.774)
	10	0.7228	0.7121	0.6713	0.7165	0.7164	0.7230	0.7174	(0.647, 0.793)	(0.631, 0.786)	(0.593, 0.743)	(0.636, 0.788)	(0.638, 0.788)	(0.645, 0.792)	(0.638, 0.787)
	20	0.7586	0.7399	0.6876	0.7470	0.7464	0.7606	0.7513	(0.686, 0.825)	(0.660, 0.813)	(0.608, 0.766)	(0.672, 0.820)	(0.670, 0.820)	(0.686, 0.828)	(0.677, 0.822)
	50	0.7830	0.7466	0.6976	0.7676	0.7587	0.8011	0.7809	(0.719, 0.842)	(0.663, 0.819)	(0.627, 0.769)	(0.692, 0.837)	(0.681, 0.831)	(0.735, 0.858)	(0.713, 0.843)
	100	0.7951	0.7464	0.7042	0.7641	0.7244	0.8397	0.8037	(0.726, 0.858)	(0.665, 0.827)	(0.630, 0.770)	(0.685, 0.834)	(0.635, 0.806)	(0.778, 0.892)	(0.731, 0.866)
	150	0.8019	0.7482	0.7099	0.7171	0.6889	0.8677	0.8206	(0.739, 0.860)	(0.656, 0.832)	(0.636, 0.775)	(0.627, 0.802)	(0.591, 0.778)	(0.811, 0.917)	(0.755, 0.883)
	200	0.8044	0.7488	0.7122	0.5718	0.5466	0.8877	0.8312	(0.739, 0.863)	(0.663, 0.823)	(0.642, 0.780)	(0.485, 0.680)	(0.476, 0.634)	(0.838, 0.933)	(0.763, 0.890)

AUC, area under the receiver operating characteristic curve; PW, pairwise; SW, stepwise; MM, min–max; MVN, multivariate normal; LR, logistic regression; LASSO, Least Absolute Shrinkage and Selection Operator.

(n₀, n₁), sample sizes in healthy/diseased groups.

p, the number of markers.

The settings of these two simulations only differ in the markers’ mean vectors. However, this small difference has led to noticeable changes in performance among PW, ridge, and LASSO methods. This observation demonstrated that the comparison among these three methods is complicated and depend intrinsically on the effect sizes and covariance structures of the markers.

4.1.3. Multivariate gamma distributions with multiple weak markers

To investigate the performance of the combination methods under skewed distributions, we simulated data from gamma distribution. The density function of gamma distribution can be parametrized by shape parameter α and rate parameter β:

$$f_{\mathit{Gamma}}(x;\alpha ,\beta )=\frac{{\beta }^{\alpha }{x}^{\alpha -1}{e}^{-\beta x}}{\mathrm{\Gamma }(\alpha )},$$

where Γ is the gamma function.

In this simulation study, we assume the shape parameter α₀ = α₁ = 10 for both populations. For the healthy group, the rate parameter is set to be β₀ = 5 for all markers and for the diseased group, distributed evenly within β₁ ∈ (4.8, …, 4.2), corresponding to marginal AUC ∼ (0.536, …, 0.648). For another setting, shape parameters are set as α₀ = 10 and α₁ ∈ (10.2, …, 11.8) and rate parameter β₀ = β₁ = 4 for both populations, corresponding to marginal AUC ∼ (0.523, …, 0.651) (results not shown). The covariate matrices were generated using normal copula with exchangeable correlation as Σ₀ = Σ₁ = 0.85I_p×p+0.15J_p×p for both populations in scenarios with equal covariances and Σ₁ = 0.85I_p×p+0.15J_p×p for the diseased population in scenarios with unequal covariances. The simulation results were presented in Table III.

Table III.

Estimated AUC and its 95% confidence intervals. Gamma distribution α₀ = 10, β₀ = 5 for healthy and α₁ = 10, β₁ = (4.8, …, 4.2) for diseased population.

		Mean AUC							Confidence interval
(n0, n1)	p	PW	SW	MM	MVN	LR	Ridge	LASSO	PW	SW	MM	MVN	LR	Ridge	LASSO
Σ0 = Σ1 = 0.85Ip×p + 0.15Jp×p (equal covariance in diseased and healthy groups)
(25,25)	10	0.6594	0.6363	0.6529	0.6404	0.6404	0.6731	0.6294	(0.477, 0.813)	(0.467, 0.795)	(0.469, 0.803)	(0.469, 0.798)	(0.475, 0.798)	(0.493, 0.821)	(0.488, 0.797)
	20	0.6822	0.6398	0.6602	0.6332	0.6216	0.6962	0.6428	(0.494, 0.838)	(0.469, 0.795)	(0.477, 0.810)	(0.466, 0.786)	(0.464, 0.773)	(0.520, 0.851)	(0.470, 0.816)
	50	0.7111	0.6356	0.6864	0.5811	0.5686	0.7270	0.6635	(0.523, 0.853)	(0.462, 0.798)	(0.498, 0.838)	(0.458, 0.739)	(0.458, 0.715)	(0.558, 0.861)	(0.491, 0.829)
	100	0.7330	0.6306	0.6956	0.6614	0.5682	0.7560	0.6756	(0.555, 0.870)	(0.459, 0.808)	(0.515, 0.835)	(0.482, 0.818)	(0.453, 0.704)	(0.622, 0.885)	(0.500, 0.835)
	200	0.7542	0.6201	0.7161	0.7259	0.5704	0.7788	0.6914	(0.582, 0.879)	(0.462, 0.794)	(0.548, 0.856)	(0.552, 0.858)	(0.456, 0.723)	(0.648, 0.893)	(0.500, 0.844)
(100,100)	10	0.7038	0.6915	0.6701	0.6960	0.6960	0.7043	0.6979	(0.624, 0.773)	(0.612, 0.764)	(0.591, 0.742)	(0.620, 0.767)	(0.619, 0.769)	(0.631, 0.772)	(0.618, 0.768)
	20	0.7272	0.7025	0.6815	0.7112	0.7111	0.7285	0.7177	(0.654, 0.799)	(0.613, 0.782)	(0.600, 0.752)	(0.627, 0.786)	(0.628, 0.787)	(0.652, 0.801)	(0.638, 0.790)
	50	0.7516	0.7063	0.7007	0.7269	0.7211	0.7652	0.7452	(0.684, 0.818)	(0.618, 0.787)	(0.624, 0.770)	(0.648, 0.798)	(0.639, 0.794)	(0.694, 0.829)	(0.669, 0.812)
	100	0.7618	0.7074	0.7136	0.7219	0.6860	0.7997	0.7637	(0.693, 0.829)	(0.622, 0.794)	(0.636, 0.783)	(0.629, 0.796)	(0.593, 0.773)	(0.736, 0.860)	(0.694, 0.829)
	200	0.7692	0.7089	0.7273	0.5588	0.5418	0.8437	0.7858	(0.701, 0.837)	(0.615, 0.791)	(0.660, 0.790)	(0.476, 0.650)	(0.479, 0.629)	(0.788, 0.895)	(0.714, 0.853)
Σ0 = 0.9Ip×p + 0.1Jp×p and Σ1 = 0.85Ip×p + 0.15Jp×p (unequal covariance)
(25,25)	10	0.6637	0.6414	0.6541	0.6451	0.6450	0.6772	0.6327	(0.485, 0.818)	(0.472, 0.802)	(0.482, 0.797)	(0.470, 0.800)	(0.472, 0.805)	(0.504, 0.827)	(0.490, 0.802)
	20	0.6892	0.6485	0.6600	0.6376	0.6260	0.7025	0.6465	(0.510, 0.840)	(0.475, 0.810)	(0.472, 0.808)	(0.470, 0.789)	(0.461, 0.784)	(0.534, 0.851)	(0.467, 0.821)
	50	0.7218	0.6397	0.6795	0.5806	0.5697	0.7357	0.6732	(0.536, 0.866)	(0.474, 0.808)	(0.493, 0.829)	(0.453, 0.741)	(0.454, 0.715)	(0.574, 0.869)	(0.500, 0.835)
	100	0.7462	0.6377	0.6845	0.6689	0.5692	0.7673	0.6836	(0.578, 0.882)	(0.464, 0.797)	(0.499, 0.822)	(0.491, 0.826)	(0.446, 0.706)	(0.634, 0.893)	(0.500, 0.842)
	200	0.7698	0.6229	0.6966	0.7379	0.5723	0.7889	0.6993	(0.610, 0.896)	(0.474, 0.808)	(0.519, 0.847)	(0.568, 0.867)	(0.453, 0.725)	(0.656, 0.896)	(0.500, 0.856)
(100,100)	10	0.7080	0.6969	0.6689	0.7009	0.7010	0.7086	0.7024	(0.629, 0.775)	(0.616, 0.768)	(0.586, 0.744)	(0.625, 0.773)	(0.625, 0.774)	(0.635, 0.777)	(0.623, 0.771)
	20	0.7351	0.7114	0.6788	0.7177	0.7180	0.7349	0.7243	(0.664, 0.806)	(0.624, 0.786)	(0.597, 0.754)	(0.634, 0.791)	(0.633, 0.792)	(0.658, 0.807)	(0.646, 0.797)
	50	0.7628	0.7192	0.6949	0.7321	0.7266	0.7724	0.7535	(0.695, 0.826)	(0.635, 0.798)	(0.620, 0.763)	(0.652, 0.804)	(0.646, 0.798)	(0.702, 0.835)	(0.680, 0.819)
	100	0.7742	0.7186	0.7037	0.7239	0.6875	0.8051	0.7718	(0.709, 0.841)	(0.638, 0.800)	(0.630, 0.773)	(0.632, 0.797)	(0.593, 0.773)	(0.743, 0.865)	(0.704, 0.836)
	200	0.7825	0.7210	0.7119	0.5594	0.5421	0.8462	0.7924	(0.715, 0.845)	(0.625, 0.802)	(0.640, 0.780)	(0.482, 0.654)	(0.478, 0.629)	(0.789, 0.899)	(0.721, 0.858)

AUC, area under the receiver operating characteristic curve; PW, pairwise; SW, stepwise; MM, min–max; MVN, multivariate normal; LR, logistic regression; LASSO, Least Absolute Shrinkage and Selection Operator.

(n₀, n₁), sample sizes in healthy/diseased groups.

p, the number of markers.

In both equal and unequal covariance scenarios, the simulation results showed similar trend as that observed for normal distribution in the previous section. This suggests that for skewed distributions such as the multivariate gamma distribution, PW, ridge, and LASSO perform generally better than other combination methods when the sample size is not order of magnitude greater than the number of markers and generally yields the larger mean of AUCs.

4.1.4. Multivariate beta distribution with multiple weak markers

Beta distribution is another widely used distribution for modeling random variables with limiting interval including percentages and proportions. In this simulation, our goal is to investigate the performance of the methods when markers are not unimodal. This can be achieved by choosing the marginal distributions parameters such that the distributions are bimodal. The density function of beta distribution can be parametrized by shape parameters α and β:

$$f_{\mathit{Beta}}(x;\alpha ,\beta )=\frac{x^{\alpha -1}{(1-x)}^{\beta -1}}{B(\alpha ,\beta )},$$

where B is the beta function.

Assume the healthy sample is from multivariate beta distribution with parameters α₀ = 0.4, β₀ = 0.6, and the diseased sample from multivariate beta distribution with parameters α₁ = (0.45, …, 0.6), β₁ = 1−α₁, corresponding to marginal AUC ∼ (0.543, …, 0.668). Both equal and unequal covariance matrices were generated using normal copula with exchangeable correlation, with Σ₀ = Σ₁ = 0.85I_p×p + 0.15J_p×p for both healthy and diseased populations in scenarios with equal covariance, and Σ₁ = 0.85I_p×p + 0.15J_p×p for the diseased population in scenarios with unequal covariance. The simulation results were listed in Table IV. For multivariate beta distribution, we observed a similar trend as that in multivariate gamma distributions for both equal and unequal covariances.

In summary, the performance of all the methods are generally comparable when only a few markers are combined. When the number of markers increases, the PW, ridge, and LASSO methods start to dominate over other combination methods. When the number of markers involved continues to grow, there are different levels of performance drop for MVN, LR, and SW methods; on the other hand, such performance drop is not observed for PW, ridge, LASSO, and MM methods, with MM method producing smaller AUCs. The performance differences among PW, ridge, and LASSO methods seem to be intrinsically depending on the effect sizes and covariance structures of the markers.

4.2. Investigation of the overfitting and estimation of bias

The remarkably different performances of these combination methods warrant further investigation. For this purpose, it is of interest to compare the performances of these combination methods with respect to the theoretical values. As described in Section 3.4, we evaluate the methods using independent validation scheme, that is, training set and testing set were independently generated from the same underlying distribution with a given parameter set and sample size. Here, we focused on scenarios of multivariate normal with common covariance as presented in the first simulation. Under such scenarios, the theoretical likelihood ratio is the universally optimal combination that has the highest sensitivity for any given specificity among all possible combinations [9]. In addition, the likelihood ratio, the Fisher’s linear discrimination, and the logistic regression are theoretically equivalent, guaranteed by the Neyman–Pearson Lemma as pointed out in [11]. The theoretical AUC of the optimal linear marker combination can be calculated based on the covariance matrices as in Equation (3). The details for computing the inverse of matrix under exchangeable correlation structure are presented in the Appendix.

Figure 2a presents the estimated AUC of the optimally combined markers by different combination methods in comparison with the theoretic values (presented as black dots) for the training set. The AUCs by each combination method was calculated by applying the combination coefficients estimated from training set to the same dataset. From the plot, we can see that when the number of markers involved are relatively small (< 10), all methods produce AUCs close to, but slightly larger than, theoretical values, except those by MM method. When the number of markers increases, all methods have different levels of increases in AUCs. Among them, MVN and LR methods generate much larger AUC than theoretical values, which are clearly over-optimistic (e.g., AUC = 1). The AUCs generated by SW method are smaller than those by MVN and LR. Ridge and LASSO are closer, but the AUCs are still larger than the theoretical values. PM method gives smaller AUCs that are closest to (albeit still above) the theoretical values. Among them, the MM method produces the smallest AUCs, which are below the theoretical ones.

Figure 2.

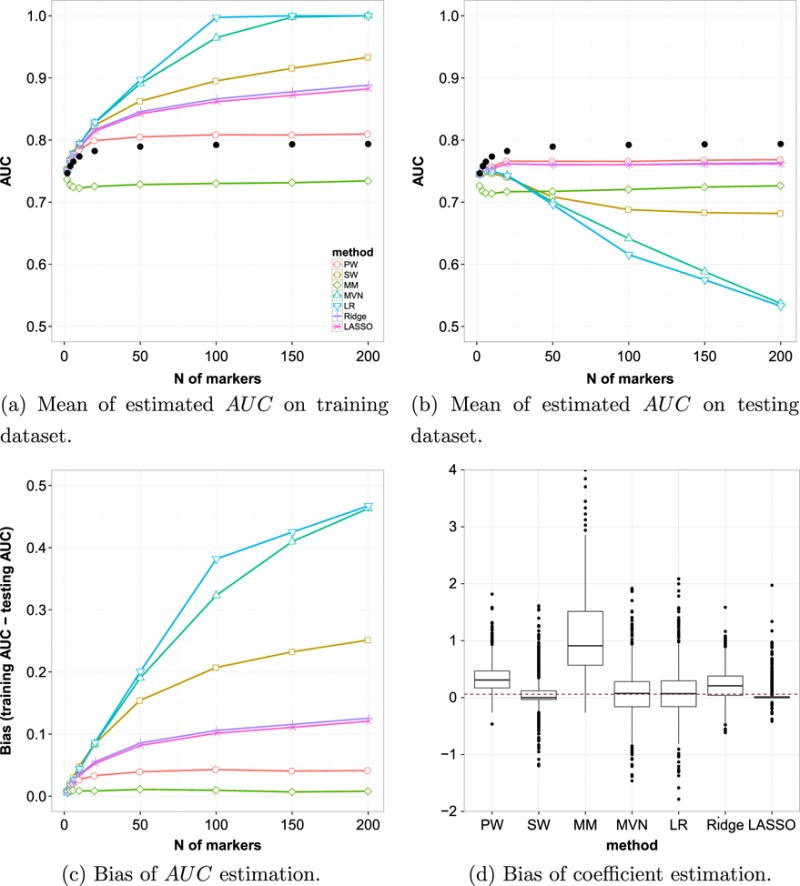
Overfitting and estimation bias. Simulated data with multivariate normal distribution with μ₁ = (0.4, …, 0.9)^T and equal covariance of Σ₁ = Σ₀ = 0.85I_p×p + 0.15J_p×p. Samples size is 100 in each group, and the number of markers p ranges from 2 to 200. Black dots in (a) and (b) indicate the theoretical optimal AUC value based on Su and Liu’s theorem (Appendix). The boxplot in (d) shows the estimated coefficients when the number of markers = 50 and the number of samples = 100 in each group.

This apparent superiority of estimated value over the theoretical optimal value is the result of estimation bias because of the fact that we estimated the performance of the classifier (the AUC of the combined marker) using the same data that created the classification rule (the combination coefficients). Such bias is not significant with large sample size when only a small number of markers were involved. However, it becomes significant when the number of markers grow. It is well-known that using re-substitution methods to estimate AUC for the purpose of comparing between combination methods might be misleading [12]. The independent validation approach in our simulation study makes it possible to assess this effect.

Figure 2b compares the estimated optimal AUCs obtained using independent validation approach with respect to the theoretic values. To be specific, the AUC of each combination method is calculated by applying the combination coefficients estimated from training set to the independently generated testing set. We can see all estimated AUCs are smaller than the theoretical value. When only a few markers are involved, the combination methods generally produce AUCs close to the theoretical values, consistent with previous observations [11, 12, 34]. When the number of markers increases, the difference becomes larger, but the level of deviation differs. Among them, severe decline in the AUCs are observed for MVN and LR methods, indicating their combination coefficients estimated from the training set are likely overfitted. The AUCs generated by PW, ridge, and LASSO methods were closest to (albeit still smaller than) the theoretical values. The MM method produces the smallest AUCs and the SW method is in the middle.

In theory, the AUCs from LR and MVN should be identical to the true value (black dots) under the scenarios presented here (multivariate normal with common covariance). Although asymptotically true, any natural fluctuations in finite sample might produce bias to the real value in the coefficient estimation. As observed in Figure 2b, any such bias could result in loss of efficiency in reaching the optimal AUC by the combined marker. Overfitting could significantly aggregate this effect, which is in line with the previous observations [11, 12, 34]. As a side note, the observed differences between LR and MVN methods are direct results of the different procedures used in estimation. In MVN method, the sample variance–covariance matrices were calculated separately for the two groups. The Moore–Penrose generalized inverse of their sum, together with the difference of the sample means, are used to produce estimated coefficients. This will produce coefficients different from those through logistic regression, which estimates the coefficients based on generalized least square regression. While the difference is subtle with few markers and larger sample sizes, it will become more noticeable when the number of markers increases.

The size of bias in estimated AUC between training set and future observation can be seen more clearly in Figure 2c. From the plot, we can see that when the number of markers involved are relatively small, all methods are capable to produce relatively small estimation difference. When the sample size is not magnitude greater than the number of markers, the estimation difference increased drastically for MVN, LR, and SW methods, up to ∼ 0.4 in LR and MVN methods and ∼ 0.2 in SW method. On the other hand, much less increases of estimation difference were observed in PW, ridge, LASSO, and MM methods (∼ 0.1). While the MM method has the least estimation difference in all scenarios, its performance is generally less favorable. Such a consistent underestimation of AUC might be due to the fact that MM method exploited less marker information than the other methods. Similar trend of estimation difference between training and testing for each method was also observed under other joint distributions of markers (data not shown).

Finally, it is important to evaluate the bias of estimated coefficients to its theoretical value. Generally, this is difficult as different theoretical values may exist for markers with different marginal AUCs. However, under the scenarios presented here (one moderate marker and multiple weak markers with equal marginal AUCs and equal covariance matrices), the theoretical value of the risk coefficients are the same for all markers except the moderate one (which has a theoretical value of 1). Another difficulty lies in the fact that the optimal coefficients are not unique, in the sense that any sets differing by a scalar multiplier would be equivalent in creating a combined marker that produce the same AUC. To overcome this complexity, we scaled the estimated coefficient vector by the top marker to make the estimated and theoretical values comparable for the other selected marker. A scenario with number of markers p = 50 and sample size N = 100 in each group is shown in Figure 2d. The dashed line indicates the theoretical value (0.06). It is worth to point out that in MM method the coefficients do not belong to fixed markers. Instead, they belong to the minimum and maximum observed values of each subject. Therefore, it cannot be compared with the rest directly. Nevertheless, we include it here for completeness. From the figure, we can see that SW and LASSO methods have smaller ranges between the first and third quartiles, with medians smaller than the theoretical value and a large number of outliers. While MVN and LR methods have their medians very close to the expected value, their ranges are notably larger. The PW and ridge methods lay somewhat in the middle, with smaller variation but larger bias. This is consistent with the bias–variance tradeoff observed in statistical method comparisons.

In summary, at the settings with small number of markers, the estimation of AUC by the combination methods are generally comparable between training set and testing set, and close to the theoretic values. When the number of markers increases, the PW, ridge, and LASSO methods provide estimation closest to the theoretical optimal value in the testing dataset. Compared with MVN, LR, and SW methods, these three methods have much smaller estimation difference between training set and testing set. While the estimation difference by MM method is smallest, its performance is less favorable. Therefore, compared with other methods, the PW, ridge, and LASSO methods have a better balance in yielding a combined marker with better AUC while maintaining a smaller estimation difference. Among them, PW method is a non-parametric one and does not rely on regression, which may become favorable under certain circumstances.

5. The example: revisited

In this section, we applied the existing and newly proposed parametric and non-parametric methods to the datasets used to develop and validate MammaPrint^® custom assay. These include the data from 78 patients used to establish the 70-gene signature [16], 84 samples used in the clinical validation by Glas et al. [18], and 307 patients used for independent validation by Buyse et al. [19]. We present the details of these datasets in Table V. For each of the three datasets, we applied each combination method and obtained the estimated combination coefficients (λ). The combination coefficients λ are then applied to the other independent datasets to obtain the ROCs and calculate the AUCs of the combined markers. In order to investigate the estimation difference, we also apply the combination coefficients estimated from training set to the same dataset. The 95% CIs of AUC were estimated based on 2000 bootstrapping sampling methods.

Table V.

Sample sizes of the MammaPrint^® datasets.

Source	Dataset	Metastatic event
		False	True	All
Glas	Glas78	44	34	78
	Glas84	72	12	84
Buyse	Buyse307	260	47	307
All		376	93	469

The results were summarized in Table VI. It can be seen that, for the independent testing datasets, PW, ridge, and LASSO methods produce the highest AUC among the methods. The combined AUCs based on PW method are comparable or better than ridge and LASSO in most cases. It is also the only one with AUC consistently higher than 0.55 at 95% significant level. Furthermore, compared with SW, MVN, and LR methods, we can see that PW, ridge, and LASSO generally has smaller estimation difference between testing set and training set. Over-optimistic estimation (AUC = 1) were observed for MVN and LR methods in some training sets. While MM method is relatively stable between testing set and training set, it yields a smaller AUC than PW, ridge, and LASSO in all cases. These observations are largely consistent with the results we have obtained in the simulation studies.

Table VI.

The estimated AUC and its 95% CIs on MammaPrint datasets by different methods.

Train set	Test set	PW	SW	MM	MVN	LR	Ridge	LASSO
Glas78	Buyse307	0.72 (0.65, 0.78)	0.65 (0.57, 0.73)	0.48 (0.39, 0.57)	0.56(0.47, 0.65)	0.55 (0.45, 0.64)	0.70 (0.62, 0.77)	0.69 (0.61, 0.76)
	Glas84	0.70 (0.55, 0.83)	0.62 (0.43, 0.78)	0.65 (0.48, 0.81)	0.61(0.45, 0.75)	0.59 (0.42, 0.75)	0.65 (0.46, 0.83)	0.62 (0.44, 0.80)
	Glas78	0.91 (0.84, 0.97)	0.99 (0.98, 1.00)	0.51 (0.39, 0.64)	1.00 (1.00, 1.00)	1.00 (1.00, 1.00)	1.00 (1.00, 1.00)	0.98 (0.95, 1.00)
Glas84	Buyes307	0.69 (0.61, 0.76)	0.64 (0.56, 0.72)	0.55 (0.46, 0.64)	0.57 (0.48, 0.65)	0.57 (0.49, 0.66)	0.69 (0.62, 0.76)	0.64 (0.56, 0.73)
	Glas78	0.77 (0.66, 0.86)	0.67 (0.55, 0.79)	0.50 (0.37, 0.63)	0.60 (0.48, 0.73)	0.56 (0.43, 0.70)	0.81 (0.71, 0.90)	0.79 (0.68, 0.89)
	Glas84	0.94 (0.87, 0.98)	0.99 (0.96, 1.00)	0.65 (0.51, 0.78)	1.00 (1.00, 1.00)	1.00 (1.00, 1.00)	0.95 (0.89, 0.99)	0.86 (0.71, 0.96)
Buyse307	Glas78	0.80 (0.69, 0.89)	0.74 (0.62, 0.85)	0.49 (0.36, 0.63)	0.71 (0.59, 0.82)	0.76 (0.64, 0.87)	0.82 (0.72, 0.91)	0.82 (0.72, 0.90)
	Glas84	0.71 (0.56, 0.83)	0.57 (0.38, 0.75)	0.64 (0.48, 0.78)	0.61 (0.46, 0.76)	0.57 (0.39, 0.73)	0.68 (0.52, 0.83)	0.56 (0.41, 0.71)
	Buyse307	0.76 (0.69, 0.82)	0.88 (0.83, 0.91)	0.55 (0.46, 0.63)	0.91 (0.88, 0.94)	0.92 (0.87, 0.96)	0.82 (0.76, 0.87)	0.82 (0.75, 0.87)

AUC, area under the receiver operating characteristic curve; PW, pairwise; SW, stepwise; MM, min–max; MVN, multivariate normal; LR, logistic regression; LASSO, Least Absolute Shrinkage and Selection Operator.

The cases using re-substitution are italicized.

6. Summary and discussion

In this paper, we empirically studied the performances of a newly proposed pairwise combination method, together with several existing parametric and non-parametric combination methods, for finding the optimal linear combination of biomarkers to maximize AUC under the new settings where more than a few biomarkers were involved, the involved biomarkers are relatively weak, and the sample sizes are not order of magnitude greater than the number of biomarkers. Such settings are not uncommon in the diagnostic/prognostic assays developed from the new generation of biotechniques (for a most recent example, see [45]), and it has brought new statistical challenges that need to be addressed. Through simulation and real data, we demonstrated that the existing methods have different drawbacks under the new settings. For MVN, LR, and, to a lesser extent, SW methods, overfitting becomes a major challenge in proper estimation of the risk coefficients and may produce over-optimistic estimation of the combined AUC in the training dataset and poorer performance in the future observations (independently generated testing dataset). On the other hand, the min–max method may underestimate the AUC without fully utilizing potentially important information existing in all biomarkers. The ridge, LASSO, and newly proposed PW combination methods strike a better balance between potential overfitting risks and insufficient utilization of marker information and has been shown to produce improved performance in both simulated scenarios and real data example when the estimated coefficients were applied to future observations. The PW method is computationally efficient and robust as a non-parametric method and has been shown to produce comparable results with the ridge and LASSO methods in certain scenarios. However, it should be pointed out that no single method examined here showed universal superiority and reached theoretic optimal value in the testing set, highlighting the difficulty and the complexity of biomarker combination under such settings.

For the PW method described in this paper, we have used empirical AUC as the optimization objective function and grid search method for finding the optimal linear combination of biomarkers. There exists a variety of alternative statistical measurements of diagnosis/prognosis accuracy and combination optimization methods other than the one shown here. Depending on the need, partial AUC, accuracy, Youden index, and many other quantities can also be used as objective function [46]. In addition, different optimization methods other than grid search, such as logistic regression, may be used depending on the nature of the biomarkers. Marker selection can also be achieved through the PW method. After the anchor marker was chosen, combination coefficients corresponding to some additional markers can be set to zero if certain criteria were not met, resulting in the elimination of these markers. For example when the coefficient is not statistically different to zero, or when the AUC of the combined marker is not statistically larger than that by the anchor marker alone. By design, the pairwise method reduced the overall computational complexity and can be easily parallelized. Hence, it is computationally tractable in the case of higher dimension of biomarkers and larger sample sizes, especially in the cases where bootstrapping method are used for parameter estimation. These potential expandability and flexibility of the proposed method is available to the users in our implemented R package.

The choice of alternative objective functions and maximization procedures in PW method would certainly have an impact on the selection of anchor marker. It is even possible that pre-existing knowledge would dictate the choice of the anchor marker. In addition, cross-validation methods may be used to improve the robustness of the anchor marker selection. In fact, in our implemented R package, we make it possible for the user to define the method for anchor marker selection or to dictate any given marker as the anchor marker.

In this paper, we did not discuss another very important group of scenarios when the true signals are sparse among the combined markers. In other words, some of the markers might be non-discriminatory with the theoretical marginal AUC = 0.5. However, our primary focus in the current work is on clinically established marker arrays that presumably consist of only real markers, and no further marker selection is needed. On the other hand, we recognize that such sparse-signal signals are not uncommon in biomarker development and discovery researches, and will investigate the performance of combination methods under such scenarios in follow-up studies.

To conclude, although re-substitution method has been widely used in traditional settings, it may produce an overly optimistic estimation when applied to new data. It is critical to control such bias, ideally by utilizing independent dataset for validation. On the other hand, overfitting in statistical model is a well-known phenomenon, yet less of a concern in both parameter estimation and performance evaluation under more traditional clinical statistics settings, where only a few strong markers were involved. Existing methods such as MVN and LR developed under such settings may not be most suitable when directly applied to the new setting, where the data presented new challenges including higher dimension of biomarkers with weak discriminatory power and limited sample sizes. Depending on the nature of markers and their covariance structure, regularized regression methods such as ridge and LASSO may be applied to ease the impact of overfitting and provide more satisfactory results. The proposed pairwise combination method, owing to its non-parametric nature, its simplicity, and flexibility, may also be a potentially useful methods in certain cases. As indicated by the complexity of conclusions under different scenarios, further in-depth investigation is needed for a better understanding of the tradeoff between model fitting, computational complexity, and information extraction.

R package is available upon request from L. Y. (li.yan@roswellpark.org).

Appendix A: the optimal AUC under multivariate normal distribution with compound symmetry

In order to derive theoretical optimal AUC in Equation (3), first we introduce the following lemma:

Lemma 1

(Inverse of matrix with compound symmetry)

Let I_m be the p-dim identity matrix and J_m matrix of ones. The inverse of a matrix in the form of αI_m+βJ_m, if it exists, is $\frac{1}{\alpha }{\mathit{I}}_m-\frac{\beta }{\alpha (\alpha +m\beta )}{\mathit{J}}_m$.

Proof

$$(\alpha I_m+\beta J_m)\cdot \left(\frac{1}{\alpha }{I}_m-\frac{\beta }{\alpha (\alpha +m\beta )}{J}_m\right)=I_m-\frac{\beta }{\alpha +m\beta }{J}_m+\frac{\beta }{\alpha }{J}_m-\frac{{\beta }^2}{\alpha (\alpha +m\beta )}{J}_m\times J_m=I_m+\left(-\frac{\beta }{\alpha +m\beta }+\frac{\beta }{\alpha }-\frac{m{\beta }^2}{\alpha (\alpha +m\beta )}\right)J_m=I_m$$

□notice J_m × J_m = mJ_m.

Theorem 1

(Inverse of covariance matrix with compound symmetry correlation)

The inverse of a covariance matrix Σ with marginal variance of ${\sigma }_1^2,\dots ,{\sigma }_p^2$ and compound symmetry correlation R = (1 − γ)I_p + γJ_p, γ ∈ (−1, 1) is

$$\frac{1}{1-\gamma }\mathit{D}{\mathit{D}}^T-\frac{\gamma }{(1-\gamma )(1-\gamma +p\gamma )}\frac{1}{p}{\displaystyle \sum _{i=1}^p{\left({\sigma }_i^2\right)}^{-1}\mathit{J},}$$ (A.1)

where D = diag $\left({\sigma }_1^{-1},\dots ,{\sigma }_p^{-1}\right)$ is a p-dim diagonal matrix.

Proof

By definition $R_{ij}=\frac{{\sum }_{ij}}{{\sigma }_i{\sigma }_j}$, so R = DΣD^T = DΣD as D = D^T. Thus, Σ = D⁻¹R(D^T)⁻¹ = D⁻¹RD⁻¹.

It is easy to see that Σ(DR⁻¹D) = (D⁻¹RD⁻¹)(DR⁻¹D) = I when R⁻¹ exists.

Therefore,

$${\mathbf{\sum }}^{-1}=\mathit{D}{\mathit{R}}^{-1}\mathit{D}=\mathit{D}\left(\frac{1}{1-\gamma }\mathit{I}-\frac{\gamma }{(1-\gamma )(1-\gamma +p\gamma )}\mathit{J}\right){\mathit{D}}^T=\frac{1}{1-\gamma }\mathit{D}{\mathit{D}}^T-\frac{\gamma }{(1-\gamma )(1-\gamma +p\gamma )}\mathit{DJ}{\mathit{D}}^T=\frac{1}{1-\gamma }\mathit{D}{\mathit{D}}^T-\frac{\gamma }{(1-\gamma )(1-\gamma +p\gamma )}\frac{1}{p}(\mathit{DJ}){(\mathit{DJ})}^T=\frac{1}{1-\gamma }\mathit{D}{\mathit{D}}^T-\frac{\gamma }{(1-\gamma )(1-\gamma +p\gamma )}\frac{1}{p}{\displaystyle \sum _{i=1}^p{\left({\sigma }_i^2\right)}^{-1}\mathit{J}}$$

□

To reach the conclusion, first we noticed that J = J^T and JJ = pJ; thus, (DJ)(DJ)^T = DJJ^TD^T = pDJD^T.

In addition, we noticed that DJ is a matrix that consists of p identical rows of vector $\left({\sigma }_1^{-1},\dots ,{\sigma }_p^{-1}\right)$; it is easy to see that (DJ)(DJ)^T have identical elements of ${\displaystyle {\sum }_{i=1}^p{({\sigma }_i^2)}^{-1}}$, hence, the last step in the proof.