Efficient Semiparametric Inference Under Two-Phase Sampling, With Applications to Genetic Association Studies

Abstract

In modern epidemiological and clinical studies, the covariates of interest may involve genome sequencing, biomarker assay, or medical imaging and thus are prohibitively expensive to measure on a large number of subjects. A cost-effective solution is the two-phase design, under which the outcome and inexpensive covariates are observed for all subjects during the first phase and that information is used to select subjects for measurements of expensive covariates during the second phase. For example, subjects with extreme values of quantitative traits were selected for whole-exome sequencing in the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project (ESP). Herein, we consider general two-phase designs, where the outcome can be continuous or discrete, and inexpensive covariates can be continuous and correlated with expensive covariates. We propose a semiparametric approach to regression analysis by approximating the conditional density functions of expensive covariates given inexpensive covariates with B-spline sieves. We devise a computationally efficient and numerically stable EM-algorithm to maximize the sieve likelihood. In addition, we establish the consistency, asymptotic normality, and asymptotic efficiency of the estimators. Furthermore, we demonstrate the superiority of the proposed methods over existing ones through extensive simulation studies. Finally, we present applications to the aforementioned NHLBI ESP.

1. INTRODUCTION

1.1 Background

In clinical and epidemiological studies, the outcomes of interest (e.g, anthropometry measurements, lipids levels, or disease status), together with demographical and environmental variables (e.g., age, gender, smoking status, and air pollution), are typically available for all subjects. The covariates of main interest often involve genotyping, biomarker as say, or medical imaging and thus are prohibitively expensive to measure for all subjects, especially in a large study. If disease status or another discrete outcome is of primary interest, then the case-control design with an equal number of cases and controls is the most efficient one (Scott and Wild 1997). If a continuous outcome such as height is of primary interest, then a cost-effective strategy is the “extreme-tail” sampling design, whereby one selectively measures the “expensive covariates” only for subjects with extreme values of the primary outcome measure (Lin et al. 2013). In either case, the efficiency of the design can be improved by stratifying on the “inexpensive covariates”.

The case-control and extreme-tail sampling can be viewed as special cases of the two-phase, outcome-dependent design, which was first introduced by White (1982). In the first phase of this design, the outcome of interest and inexpensive covariates are observed for all study subjects; the information collected during the first phase is then used to determine which subjects to include for measurements on expensive covariates during the second phase. This design greatly reduces the cost and other burdens associated with the collection of expensive covariate data while incurring little loss of statistical efficiency and thus has been widely used in large epidemiological and clinical studies.

1.2 NHLBI ESP

Our interest in the two-phase design was motivated by the NHLBI ESP, which was designed to identify genetic variants in all protein-coding regions of the human genome that are associated with heart, lung, and blood diseases. This project performed whole exome sequencing on 4494 subjects, who were selected from seven large cohorts: the Atherosclerosis Risk in Communities (ARIC) study (The ARIC Investigators 1989); Coronary Artery Risk Development in Young Adults (CARDIA) study (Friedman et al. 1988); Cardiovascular Health Study (CHS) (Fried et al. 1991); Framingham Heart Study (FHS) (Dawber et al. 1951); Jackson Heart Study (Taylor Jr et al. 2005); Multi-Ethnic Study of Atherosclerosis (MESA) (Bild et al. 2002); and Women’s Health Initiative (WHI) (The Women’s Health Initiative Study Group 1998).

The NHLBI ESP contains several studies, each of which was focused on a particular outcome. Some of the studies selected subjects with extreme values of a quantitative trait. For example, in the body mass index (BMI) study, 659 subjects with BMI values less than 25kg/m² or greater than 40kg/m² were selected for sequencing. In the blood pressure (BP) study, 806 subjects were selected from the upper and lower 0.2%–1.0% of the BP distribution adjusted for age, gender, race, BMI, and anti-hypertensive medication. In the low-density lipoprotein (LDL) study, 657 subjects were selected because of extremely high or low values of LDL adjusted for age, gender, race, and lipid medication. These three studies are important examples of the general two-phase design, under which the second-phase selection depends on the outcome and inexpensive covariates that can be continuous and correlated with expensive covariates.

1.3 Existing Work

Several methods have been developed for regression analysis of two-phase studies. Semiparametric methods, which specify a parametric form for the regression model but allow for an arbitrary covariate distribution, are particularly appealing. In particular, Robins et al. (1995) proposed a semiparametric estimator based on inverse probability of inclusion weighting. Their approach requires every study subject to have a positive probability of being selected in the second phase and thus cannot be applied to the extreme-tail design adopted by the NHLBI ESP. In addition, their estimator can be difficult to implement in practice because it involves numerical solution of an infinite-dimensional integral equation when the outcome of interest is continuous. Lawless et al. (1999) suggested to discretize the continuous first-phase data into a small number of strata and then use the stratum membership to select subjects in the second phase. For subjects not selected in the second phase, only the stratum membership is used in the inference. Breslow et al. (2003) established the asymptotic properties of the corresponding maximum likelihood estimator (MLE). Such data discretization entails a substantial loss of information and may even bias parameter estimation.

To improve efficiency, Chatterjee et al. (2003) proposed a pseudo-score estimator (PSE), and Weaver and Zhou (2005) proposed a maximum estimated likelihood estimator (MELE). Both methods allow the outcome of interest to be continuous but require the inexpensive covariates to be discrete. Chatterjee and Chen (2007) extended the PSE method to allow for continuous inexpensive covariates in the regression analysis by using kernel smoothing but required the second-phase selection to depend on only discrete covariates. Both the PSE and MELE methods are statistically inefficient. Song et al. (2009) and Lin et al. (2013) considered efficient estimation for two-phase studies without inexpensive covariates. When the inexpensive covariates are available, however, this approach is inefficient because it disregards the inexpensive covariates for subjects not selected in the second phase. More important, this approach may yield biased estimators if the second-phase selection depends on the inexpensive covariates.

1.4 Overview

In this article, we explore efficient semiparametric estimation for regression models under general two-phase designs such that the sampling in the second phase can depend on the first-phase data in any manner. We allow the outcome variable to be discrete or continuous, and we accommodate inexpensive covariates, which can be used to improve the efficiency of the second-phase sampling, control for confounding, and evaluate interactions among the expensive and inexpensive covariates. We allow inexpensive covariates to be continuous and correlated with expensive covariates while leaving the distribution of covariates completely unspecified. Dealing with this general situation is very challenging because the likelihood function involves the conditional density functions of expensive covariates given continuous inexpensive covariates. We address this challenge by incorporating sieve approximations (Grenander, 1981) of the conditional density functions into the nonparametric likelihood function. We develop a computationally efficient and numerically stable expectation-maximization (EM) algorithm to maximize the sieve likelihood. We show the consistency, asymptotic normality, and asymptotic efficiency of the resulting estimators through a novel combination of modern empirical process theory and sieve approximation theory. We demonstrate the superiority of the proposed methods over the existing ones through extensive simulation studies. Finally, we provide detailed applications to the motivating NHLBI ESP.

2. METHODS

Let Y denote the outcome of interest, X denote the vector of expensive covariates that is measured on a fraction of subjects in the study, Z denote the vector of inexpensive covariates that is potentially correlated with X, and W denote the vector of inexpensive covariates that is known to be independent of X given Z. The data (Y, X, Z, W) are assumed to be generated from the joint distribution P_θ(Y|X, Z, W)P(X|Z)P(Z, W), where P_θ(Y|X, Z, W) is a parametric regression model indexed by parameter θ, P(X|Z) is the conditional distribution of X given Z, and P(Z, W) is the joint distribution of Z and W. For linear regression,

$$P_{\theta }(Y|X,Z,W)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{{(Y-\alpha -{\beta }^{\mathrm{T}}X-{\gamma }^{\mathrm{T}}Z-{\eta }^{\mathrm{T}}W)}^2}{2{\sigma }^2}\right\}$$

where θ = (α, β^T, γ^T, η^T,σ²)^T; for logistic regression,

$$P_{\theta }(Y=1|X,Z,W)={\left[1+\exp \left\{-\left(\alpha +{\beta }^{\mathrm{T}}X+{\gamma }^{\mathrm{T}}Z+{\eta }^{\mathrm{T}}W\right)\right\}\right]}^{-1},$$

where θ = (α, β^T, γ^T, η^T)^T The linear predictors can be modified to include the interaction terms among X, Z, and W.

Under the two-phase design, (Y, Z, W) is measured for all n subjects in the first phase, and X is measured for a sub-sample of size n₂ in the second phase. Let R indicate, by the values 1 versus 0, whether the subject is selected for the measurement of X in the second phase. We assume that the distribution of R depends on (Y, X, Z, W) only through the first-phase data (Y, Z, W). Under this assumption, the data on X are missing at random, such that the sampling indicators (R₁,…, R_n) can be omitted from the likelihood function when estimating θ. Thus, the observed-data log-likelihood takes the form

$$\begin{array}{l}{\displaystyle \sum _{i=1}^n{R}_i\left\{\log P_{\theta }\left(Y_i|X_i,Z_i,W_i\right)+\log P\left(X_i|Z_i\right)\right\}}\\ +{\displaystyle \sum _{i=1}^n\left(1-R_i\right)\log }{\displaystyle \int P_{\theta }\left(Y_i|\mathit{x},Z_i,W_i\right)P\left(\mathit{x}|Z_i\right)d\mathit{x}.}\end{array}$$ (1)

We maximize expression (1) using the nonparametric maximum likelihood estimation (NPMLE). For each distinct observed z, we estimate P(X|z) by a discrete probability function on the distinct observed values of X, denoted by x₁,…, x_m (m ≤ n₂), where m is the total number of the distinct values. Even with this discretization, maximization of expression (1) is not feasible when Z contains continuous components because then only a small number of the observations on X are associated with each z.

To tackle this challenge, we approximate P(X|z) by the method of sieves (Grenander, 1981). Specifically, we use the B-spline basis (Schumaker, 1981) to construct the approximating functions. Assuming that Z has bounded support, we center and rescale each component of Z such that it has support on [0, 1]. We then partition the interval [0,1] as $\mathrm{\Delta }\equiv \{t_{-q+1}=\dots =t_{-1}=0=t_0<t_1<\dots <t_{b_n+1}=1=\dots =t_{q+b_n}\},$ where {t_l: l = −q + 1,…,q + b_n} are the knots, q is the order of the B-spline basis, and b_n is the number of interior knots. The number b_n is determined by the first-phase sample size n. For ease of implementation, we choose the interior knots as evenly spaced partitions in [0,1] with gap 1/(b_n + 1). Let ${\{N_l^q(z)\}}_{l=-q+1}^{b_n}$ be a one-dimensional normalized B-spline basis of order q associated with ∆. We construct $N_l^q(z)$ from the recursive formula

$$N_l^q(z)=\frac{z-t_l}{t_{l+q-1}-t_l}{N}_l^{q-1}(z)+\frac{t_{l+q}-z}{t_{l+q}-t_{l+1}}{N}_{l+1}^{q-1}(z),l=-q+1,\dots ,b_{n,}$$

where $N_l^1(z)=I(t_l\le z\le t_{l+1}),l=0,\dots ,b_n.$ Figure S1 shows ${\{N_l^q(z)\}}_{l=-q+1}^{b_n}$ for q ≤ 3. We refer to ${\{N_l^1(z)\}}_{l=0}^{b_n}$, ${\{N_l^2(z)\}}_{l=-1}^{b_n}$, and ${\{N_l^3(z)\}}_{l=-2}^{b_n}$ as the histogram, linear, and quadratic bases, respectively. We then construct the multivariate B-spline basis on the support of Z as $\{N_{l_1}^q(Z_1)\dots N_{l_{d_z}}^q(Z_{d_z}),l_1,\dots ,l_{d_z}=-q+1,\dots ,b_n\},$ where Zν is the νth component of Z, and d_z is the dimension of Z. To simplify notation, we represent the B-spline basis functions in $\{N_{l_1}^q(Z_1)\dots N_{l_{d_z}}^q(Z_{d_z}),l_1,\dots ,l_{d_z}=-q+1,\dots ,b_n\},$as $\{B_j^q(Z),j=1,\dots ,{(b_n+q)}^{d_z}\}.$ Because the B-spline basis functions have local support, we approximate log P(X_i|Z_i) and P(x|Z_i) in expression (1) by ${\displaystyle {\sum }_{k=1}^{m}I(X_i=x_k){\displaystyle {\sum }_{j=1}^{s_n}{B}_j^q(Z_i)\log p_{kj}}}$ and ${\displaystyle {\sum }_{k=1}^{m}I(\mathit{x}={\mathit{x}}_k){\displaystyle {\sum }_{j=1}^{s_n}{B}_j^q(Z_i)p_{kj}}}$ respectively, where $s_n={(b_n+q)}^{d_z},$and $p_{kj}=s_n{\displaystyle \int P({\mathit{x}}_k|\mathit{z})B_j^q(\mathit{z})dz.}$

We aim to maximize the following function

$$\begin{array}{l}{l}_n(\theta ,\left\{p_{kj}\right\})={\displaystyle \sum _{i=1}^n{R}_i\left\{\log P_{\theta }(Y_i|X_i,Z_i,W_i)+{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I(X_i={\mathit{x}}_k)B_j^q(Z_i)\log p_{kj}}}\right\}}\\ +{\displaystyle \sum _{i=1}^n(1-R_i)\log \left\{{\displaystyle \sum _{k=1}^m{P}_{\theta }(Y_i|{\mathit{x}}_k,Z_i,W_i){\displaystyle \sum _{j=1}^{s_n}{B}_j^q(Z_i)p_{kj}}}\right\}}\end{array}$$ (2)

under the constraints of ${\displaystyle {\sum }_{k=1}^m{p}_{kj}=1}$ and $p_{kj}\ge 0(k=1,\dots ,m;j=1,\dots ,s_n)$ With the use of the empirical distribution function of X given Z, parameter estimation based on the maximization of expression (2) is feasible even when X is multidimensional.

Remark 1

If there are no inexpensive covariates Z and W, then the observed-data log-likelihood (1) reduces to

$${\displaystyle \sum _{i=1}^n{R}_i\left\{\log p_{\theta }(Y_i|X_i)+\log P(X_i)\right\}+}{\displaystyle \sum _{i=1}^n(1-R_i)\log {\displaystyle \int P_{\theta }(Y_i|x)P(x)dx.}}$$ (3)

Song et al. (2009) and Lin et al. (2013) maximized expression (3) using the NPMLE, where P(X) is estimated by the discrete probabilities at the observed values of X. This maximum likelihood estimation approach, denoted by MLE₀ hereafter, can be viewed as a special case of our sieve maximum likelihood estimation approach. If the inexpensive covariates are available for all subjects but the second-phase selection does not depend on either Z or W, then the MLE₀ method can be adopted by redefining the “expensive covariates” as (X^T, Z^T, W^T)^T and disregarding Z and W for subjects not selected in the second phase. This data reduction approach may entail a substantial loss of information. If the second-phase selection does depend on Z and W, then expression (3) no longer correctly reflects the sampling mechanism, and the MLE₀ method is generally biased.

We present in the Appendix a novel EM-type algorithm for maximizing expression (2) that is computationally efficient and numerically stable. We prove in Section S.1 of the Supplemental Material that the resulting sieve maximum likelihood estimator (SMLE) $\widehat{\mathit{\theta }}$ is consistent, asymptotically normal, and asymptotically efficient. Our proofs integrate techniques from modern empirical process theory and sieve approximation theory. Our framework does not require every study subject to have a positive selection probability in the second phase and thus covers a wide spectrum of two-phase designs. We provide in Section S.1 of the Supplemental Material easily-verifiable conditions on model identifiability that rely only on subjects with complete data.

The profile log-likelihood function for θ is $pl(\theta )\equiv {max}_{\{p_{kj}\}}{l}_n(\theta ,\{P_{kj}\}).$ As justified at the end of Section S.1 of the Supplemental Material, we can estimate the limiting covariance matrix of $\widehat{\theta }$ by the negative inverse of the Hessian matrix of $pl(\widehat{\theta })$ Specifically, we obtain the value of pl (θ) by holding θ fixed in the EM algorithm and obtaining the value of l_n(θ, {p_kj}) at convergence. Then, we estimate the covariance matrix of θ by the negative inverse of the matrix whose (k, l)th element is $h_n^{-2}\left\{pf(\widehat{\theta }+e_k{h}_n+e_l{h}_n)-pf(\widehat{\theta }+e_k{h}_n)-pf(\widehat{\theta }+e_l{h}_n)+pf(\widehat{\theta })\right\},$ where e_κ is the kth canonical vector, and h_n is a constant of the order n^−1/2.

3. SIMULATION STUDIES

We conducted extensive simulation studies to compare the performance of the SMLE and MLE₀ methods by mimicking the extreme-tail sampling design adopted in the NHLBI ESP. In the first set of studies, we set X = U₁, Z = rU₁ + U₂, and W = U₃, where U₁, U₂, and U₃ are independent Uniform(0,1) variables, and r is a parameter controlling the correlation between X and Z. We varied r from 0 to 0.3. We generated the outcome from the linear model: Y = 0.5X + 0.5Z + 0.5W + ε, where ε is a standard normal random variable independent of U₁, U₂, and U₃. We let n = 2000 and selected 150 subjects with the highest and 150 subjects with the lowest values of Y in the second phase. For the subjects selected in the second phase, the data consist of (Y, X, Z, W); for those not selected in the second phase, the data utilized by the SMLE and MLE₀ methods consist of (Y, Z, W) and Y, respectively. In the SMLE method, we estimated P(X|Z) using the histogram basis. We partitioned the domain of Z using evenly-spaced quantiles and varied the number of regions s_n from 5 to 15 to assess its effects on model-fitting. The results with different s_n are very similar. The maximum difference in the coverage probability of the 95% confidence interval for any parameter is only 0.5%. Therefore, we only report the results for s_n = 10. We estimated the covariance matrix of $\widehat{\theta }$ by the profile likelihood method with step size of n^−1/2.

The results of the simulation studies are summarized in Table 1. Both the SMLE and MLE₀ parameter estimators are virtually unbiased. The SMLE variance estimator accurately reflects the true variation, and the corresponding confidence intervals have reasonable coverage probabilities. The SMLE estimator is much more efficient than the MLE₀ estimator for Z and W because the SMLE method utilizes additional data on (Z, W) for those subjects not selected in the second phase. The SMLE estimator is also more efficient than the MLE₀ estimator for X, and the efficiency gain increases as the correlation between X and Z increases. We also considered larger first-phase sample sizes and reported the results in Table S1. By comparing the results in Tables 1 and S1, we see that the relative efficiencies of the SMLE estimators to the MLE₀ estimators increase as the first-phase sample size increases, i.e., the second-phase sampling becomes more extreme.

Table 1.

Simulation Results Under the Model Y = 0.5X + 0.5Z + 0.5W + ε With the Second-Phase Sample Selection Depending Only on Y

r	Covariate	SMLE					MLE0
		Bias	SE	SEE	CP	RE	Bias	SE
0.0	X	0.004	0.112	0.108	0.943	1.029	0.005	0.114
	Z	0.001	0.082	0.083	0.951	1.923	0.006	0.114
	W	−0.001	0.078	0.078	0.952	2.126	0.005	0.114
0.1	X	0.005	0.112	0.109	0.941	1.036	0.004	0.114
	Z	0.004	0.081	0.082	0.951	1.973	0.006	0.114
	W	−0.001	0.078	0.078	0.952	2.153	0.005	0.115
0.2	X	0.005	0.112	0.109	0.945	1.077	0.004	0.116
	Z	0.005	0.081	0.082	0.952	2.029	0.006	0.115
	W	−0.001	0.078	0.078	0.952	2.167	0.005	0.115
0.3	X	0.004	0.114	0.111	0.945	1.104	0.005	0.119
	Z	0.005	0.081	0.082	0.952	2.056	0.006	0.116
	W	−0.001	0.078	0.078	0.953	2.189	0.005	0.115

NOTE: Bias and SE are, respectively, the empirical bias and standard error of the parameter estimator; SEE is the empirical mean of the standard error estimator; CP is the coverage probability of the 95% confidence interval; RE is the empirical variance of MLE₀ over that of SMLE. Each entry is based on 10,000 replicates.

In the second set of simulation studies, we generated the data from the model Y = 0.5X + 0.5Z + 0.5W + 0.4XW + ε. The results are summarized in Table 2. The SMLE estimator is much more efficient than the MLE₀ estimator for all covariates. In addition, the relative efficiency of the SMLE estimator to the MLE₀ estimator for X is much higher with the interaction term than without the interaction term in the regression model.

Table 2.

Simulation Results Under the Model Y = 0.5X + 0.5Z + 0.5W + 0.4XW + ε With the Second-Phase Sample Selection Depending Only on Y

r	Covariate	SMLE					MLE0
		Bias	SE	SEE	CP	RE	Bias	SE
0.0	X	0.009	0.225	0.214	0.935	1.207	0.010	0.248
	Z	0.001	0.087	0.087	0.950	1.885	0.008	0.120
	W	0.005	0.208	0.199	0.941	1.400	0.011	0.246
	XW	−0.008	0.388	0.374	0.941	1.275	0.001	0.438
0.1	X	0.012	0.224	0.213	0.934	1.244	0.011	0.250
	Z	0.006	0.086	0.086	0.951	1.972	0.007	0.121
	W	0.005	0.206	0.199	0.944	1.454	0.012	0.248
	XW	−0.009	0.385	0.372	0.940	1.321	0.000	0.443
0.2	X	0.011	0.220	0.211	0.935	1.316	0.011	0.252
	Z	0.007	0.084	0.085	0.949	2.082	0.007	0.122
	W	0.005	0.202	0.196	0.943	1.535	0.012	0.251
	XW	−0.009	0.377	0.365	0.941	1.396	0.000	0.446
0.3	X	0.009	0.218	0.209	0.938	1.387	0.011	0.256
	Z	0.007	0.083	0.084	0.950	2.147	0.007	0.122
	W	0.004	0.199	0.192	0.944	1.635	0.012	0.254
	XW	−0.008	0.369	0.358	0.942	1.494	0.000	0.451

NOTE: See the Note to Table 1.

In the above two sets of simulation studies, the second-phase selection depends on the outcome only such that MLE₀ provides unbiased estimation of all parameters. If the second-phase selection depends on both the outcome and inexpensive covariates, then MLE₀ may be biased, whereas PSE (Chatterjee et al. 2003; Chatterjee and Chen 2007) is applicable provided that the sampling depends on only discrete covariates. In a third set of simulations, we compared the SMLE, MLE₀, and PSE methods in this scenario. Specifically, we set X = I(U₁ > 0.8) and $Z=I(\stackrel{\sim }{Z}>{\stackrel{\sim }{z}}_{0.80})$, where $\stackrel{\sim }{Z}=rX+U_2$, r is a parameter controlling the correlation between X and Z, U₁ and U₂ are independent Uniform(0,1), and ${\stackrel{\sim }{z}}_{0.80}$is the 80% quantile of $\stackrel{\sim }{Z}$ We generated the outcome from the model Y = X + Z + ε, where ε is a standard normal random variable independent of U₁ and U₂. In the first phase, we simulated a cohort of 4000 subjects and defined six strata according to the values of Z and Y. That is, for subjects with Z = 0, we defined three strata according to whether their values of Y are less than the 5% quantile, greater than the 95% quantile, or between these two quantiles; for subjects with Z = 1, we defined another three strata according to whether their values of Y are less than the 20% quantile, greater than the 80% quantile, or between these two quantiles. The quantiles were chosen such that each of the extreme-tail strata contained ~160 subjects. In the second phase, we only included subjects with values of Y in the four extreme-tail strata such that n₂ ≈ 640. Because Z is binary, for the SMLE method we estimated P(X|Z) by the empirical probability of X given Z. As shown in Table 3, the SMLE method is much more efficient than the PSE method, and the efficiency gain increases as the correlation between X and Z decreases. The MLE₀ parameter estimators are severely biased whether X and Z are correlated or not.

Table 3.

Simulation Results When the Second-Phase Sample Selection Depends on Both Y and Z

r	Covariate	SMLE					MLE0		PSE
		Bias	SE	SEE	CP	RE	Bias	SE	Bias	SE
0.0	X	0.005	0.074	0.073	0.952	1.307	0.291	0.096	0.006	0.085
	Z	0.000	0.047	0.047	0.947	1.146	−0.499	0.044	0.000	0.051
0.1	X	0.004	0.070	0.070	0.952	1.220	0.267	0.093	0.004	0.078
	Z	0.000	0.049	0.049	0.945	1.123	−0.556	0.041	0.001	0.052
0.2	X	0.003	0.067	0.067	0.952	1.154	0.254	0.090	0.002	0.072
	Z	0.000	0.052	0.051	0.944	1.106	−0.609	0.039	0.000	0.055
0.3	X	0.003	0.066	0.066	0.950	1.118	0.241	0.089	0.002	0.070
	Z	0.000	0.056	0.055	0.945	1.092	−0.658	0.038	0.000	0.059

NOTE: Bias and SE are, respectively, the empirical bias and standard error of the parameter estimator; SEE is the empirical mean of the standard error estimator; CP is the coverage probability of the 95% confidence interval; RE is the empirical variance of PSE over that of SMLE. Each entry is based on 10,000 replicates.

To assess the robustness of SMLE when the inexpensive covariates that are correlated with expensive covariates are misclassified as being independent of expensive covariates, we simulated data in the same setup as in the first set of studies but treated Z as independent of X in the analysis. The results are summarized in Table S2. The SMLE estimators perform reasonably well when r is small. Comparing the standard errors of the SMLE estimators for X and Z when r = 0 in Tables 1 and S2, we observe that there is virtually no efficiency loss when inexpensive covariates that are independent of expensive covariates are treated as if they were correlated with expensive covariates.

Finally, we conducted simulation studies to evaluate the performance of SMLE when Z contains more than one continuous component. Specifically, we set X = U₁ and Z = (Z₁,Z₂)^T, where Z₁ = rU₁ + U₂, Z₂ = rU₁ + U₃, U₁, U₂, and U₃ are independent Uniform(0,1) variables, and r is a parameter controlling the correlation between X and Z. We generated the outcome from the linear model: Y = 0.5X + 0.5Z₁ + 0.5Z₂ + ε, where ε is a standard normal random variable independent of U₁, U₂, and U₃. We let n = 2000 and considered two second-phase sampling strategies: the first one selected 300 subjects from the two tails of the distribution of Y; the second one selected 300 subjects from the two tails of the distribution of the residuals from the linear model relating Y to Z. We estimated P(X|Z) using the linear basis. We set b_n = 8 and partitioned the domain of Z₁ and Z₂ using evenly-spaced quantiles. The results of the simulation studies are summarized in Table S3. The SMLE method continues to perform well.

4. APPLICATIONS TO THE NHLBI ESP

The NHLBI ESP is one of the largest and most expensive genome sequencing projects conducted up to date. As mentioned in Section 1.2, this project consists of several studies, some of which selected subjects under two-phase, outcome-dependent sampling. In this section, we describe applications of the proposed methods to the single-variant analysis in the BP and LDL studies, both of which selected subjects on the basis of extreme trait values adjusted for medication and demographical variables. Exome sequencing was performed at the University of Washington and the Broad Institute using the Roche NimbleGen SeqCap EZ or Agilent SureSelect Human All Exon 50 Mb. The data were processed according to the quality control criteria described in Lin et al. (2013).

4.1 BP Study

We first considered the BP study. The first phase was comprised of 28,202 subjects from the ARIC, CARDIA, CHS, FHS, JHS, and MESA cohorts. In the second phase, 253 and 245 subjects from the upper and lower tails of the BP distribution, respectively, were selected for sequencing. The selection was not based on the original BP values, but rather the average residuals from the linear models relating diastolic and systolic BP values to age, gender, race, BMI, and anti-hypertensive medication. In addition to the 498 subjects selected from the two tails of the BP distribution, the second-phase sample also included 410 subjects from the deeply phenotyped reference (DPR) group, which is a random sample of subjects with measurements on a common set of phenotypes.

Because the original BP values were not available for those subjects without the sequence data, we considered the average BP residuals as the outcome of interest in the analysis. We included log-transformed BMI, race, age, age-squared, gender, and cohort indicators as covariates. Although BMI and race are not correlated with the BP residuals, they are potentially correlated with single-nucleotide polymorphism (SNP) genotypes and thus may provide information on SNP genotypes for those subjects without the sequence data. The other covariates are assumed to be independent of SNP genotypes given BMI and race. We verified this assumption by performing genome-wide association analysis of age, gender, and cohort indicators adjusted for log-transformed BMI and race in the DPR group (see Figure S2). Thus, when implementing the SMLE method, we let Z include log-transformed BMI and race and W include the other covariates. In the sieve approximation, we used the histogram basis because Z contains only one continuous component (i.e., log-transformed BMI). We partitioned the domain of BMI using separate evenly-spaced quantiles for the European Americans (EAs) and African Americans (AAs). In genome-wide association studies, a well-behaved quantile-quantile (QQ) plot and a close-to-one genomic control λ, which is the ratio of the observed median of the test statistics to the median of the ${{\rm X}}_1^2$ distribution, imply good model fitting and proper type I error control. We used the QQ plot and genomic control λ to select the number of regions; this resulted in three regions for the EAs and one region for the AAs (Figure S3).

We restricted our analysis to the 24,941 SNPs with minor allele frequencies (MAFs) greater than 15%. We chose the additive genetic model, under which the genetic variable codes the number of minor alleles that an subject carries at a variant site. Figure 1 shows the QQ plots for the SMLE and MLE₀ methods. Because the second-phase selection is solely determined by the outcome of interest, the MLE₀ method is valid. The SMLE method produces more significant results than the MLE₀ method. Table 4 lists the top 10 SNPs for the SMLE method. The genetic effect estimates are similar between the two methods. Correlations between log-transformed BMI and the SNP genotypes are weak. When the SNP genotypes are weakly correlated with race, the standard error estimates of the SMLE method are comparable to those of the MLE₀ method; when the SNP genotypes are strongly correlated with race, the standard error estimates of the SMLE method are much smaller than those of the MLE₀ method. These results are consistent with the theoretical and simulation results. It would be worthwhile to follow up the SNPs listed in Table 4 in larger samples.

Figure 1.

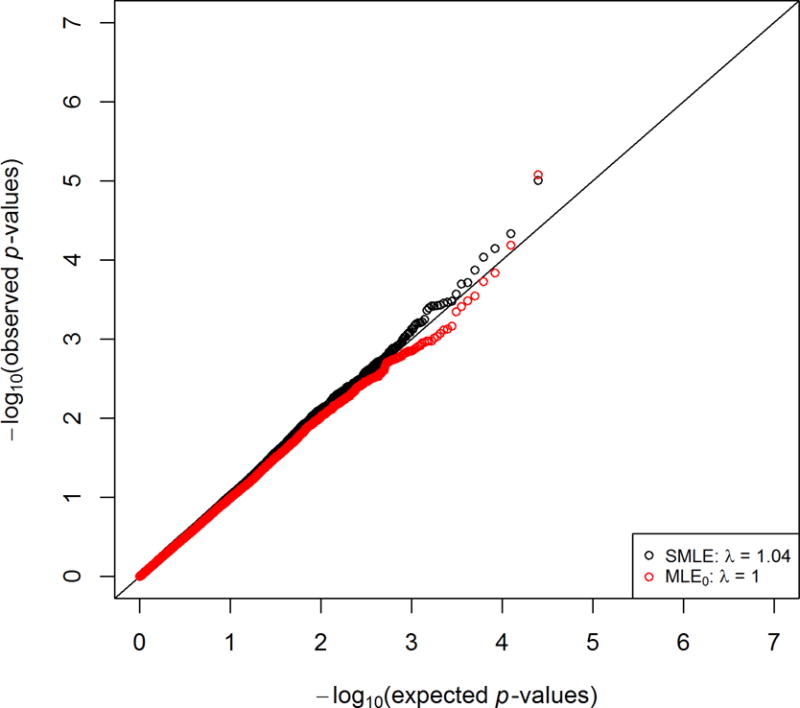
Quantile-quantile plots for the analysis of the BP study in the NHLBI ESP using the SMLE and MLE₀ methods.

Table 4.

Top 10 SNPs in the Analysis of the BP Study in the NHLBI ESP

SNP	MAF	Correlation		SMLE			MLE0
		log (BMI)	Race	Est	SE	p-value	Est	SE	p-value
18:44595809	0.43	0.00	0.11	2.04E-01	4.63E-02	9.93E-06	2.05E-01	4.61E-02	8.37E-06
18:51904644	0.25	0.00	−0.27	2.29E-01	5.63E-02	4.65E-05	2.14E-01	5.64E-02	1.47E-04
18:51904641	0.25	−0.01	−0.27	2.23E-01	5.62E-02	7.13E-05	2.09E-01	5.59E-02	1.86E-04
7:101713590	0.18	0.01	−0.02	2.58E-01	6.59E-02	9.24E-05	2.17E-01	6.63E-02	1.06E-03
18:44585955	0.38	−0.08	−0.05	1.84E-01	4.81E-02	1.34E-04	1.89E-01	4.73E-02	6.54E-05
19:7166388	0.28	0.09	0.39	2.01E-01	5.39E-02	1.93E-04	1.79E-01	5.55E-02	1.29E-03
19:8176919	0.46	0.01	−0.15	−1.66E-01	4.47E-02	2.01E-04	−1.62E-01	4.51E-02	3.29E-04
12:6464581	0.15	0.09	0.59	2.55E-01	7.00E-02	2.68E-04	2.43E-01	8.43E-02	3.93E-03
17:65720346	0.48	−0.07	−0.31	−1.65E-01	4.59E-02	3.33E-04	−1.48E-01	4.66E-02	1.49E-03
14:75590846	0.46	0.01	−0.07	1.64E-01	4.58E-02	3.42E-04	1.52E-01	4.52E-02	7.42E-04

NOTE: SNP name is in the “chromosome:position” format, where the positions are based on the human reference sequence (UCSC Genome Browser, hg19). Est and SE stand for the genetic effect estimate and standard error, respectively. Correlation pertains to the SNP and covariate.

4.2 LDL Study

We next considered the LDL study. The first phase was comprised of 49,904 subjects from the aforementioned seven cohorts. In the second phase, 604 subjects with extremely large or small values of the residuals from the linear regression of log-transformed LDL on age, gender, race, and lipid medication and 923 subjects from the DPR group were selected for sequencing. We considered log-transformed LDL as the outcome of interest and included log-transformed BMI, race, age, age-squared, gender, and cohort as covariates. As in Section 4.1, we let Z include log-transformed BMI and race and W include the other covariates. In the sieve approximation, we used the histogram basis and partitioned the domain of BMI using separate evenly-spaced quantiles for the EAs and AAs. We used the QQ plot and genomic control λ to select the number of regions; this resulted in one region for both EAs and AAs (Figure S4). When implementing the MLE₀ method, we performed both race-combined and race-stratified analysis.

We restricted our analysis to the 26,431 SNPs with MAFs greater than 15%. We chose the additive genetic model. Figure 2 shows the QQ plots using the SMLE and MLE₀ methods. The observed p-values of the SMLE method agree very well with the global null hypothesis of no association, except at the extreme right tail. By contrast, the observed p-values of both the race-combined and race-stratified MLE₀ methods deviate substantially from the null distribution, reflecting excessive false-positive results. This is because the second-phase selection is determined by both the outcome of interest and the inexpensive covariates. Incidentally, the PSE method of Chatterjee and Chen (2007) could not be applied here because it does not allow the second-phase selection to depend on continuous covariates.

Figure 2.

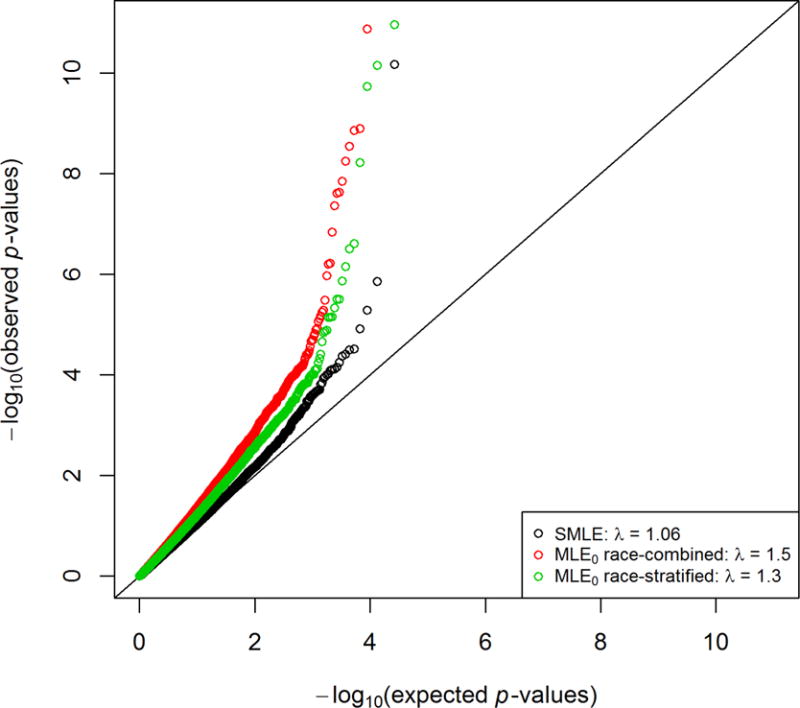
Quantile-quantile plots for the analysis of the LDL study in the NHLBI ESP using the SMLE and MLE₀ methods.

Table 5 lists the top 10 SNPs identified by the SMLE method. Two SNPs reached genomewide significance. The top SNP (19:045389174, p-value = 6.73 × 10⁻¹¹) is located in gene PVRL2 in the 19q13.32 region. This is a well-known gene region (BCAM/PVRL2/APOE/APOC1) for LDL (Sandhu et al. 2008; Sabatti et al. 2009). The second most significant SNP (17:040353722, p-value = 3.07 × 10⁻⁹) is located in gene STAT5B, which was suggested by Kornfeld et al. (2011) to play a role in the transcription regulation of hepatic cholesterol homeostasis.

Table 5.

Top 10 SNPs in the Analysis of the LDL Study in the NHLBI ESP

SNP	MAF	Est	SE	p-value
19:045389174	0.18	−6.86E-02	1.05E-02	6.73E-11
17:040353722	0.15	−3.00E-02	5.06E-03	3.07E-09
06:165715460	0.21	−4.20E-02	8.70E-03	1.38E-06
06:165715673	0.21	−3.89E-02	8.55E-03	5.23E-06
12:053823307	0.16	3.39E-02	7.74E-03	1.21E-05
06:042995211	0.26	−3.57E-02	8.57E-03	3.08E-05
07:107696289	0.20	4.26E-02	1.02E-02	3.20E-05
03:087295049	0.18	3.32E-02	8.05E-03	3.85E-05
01:216371934	0.21	−3.10E-02	7.57E-03	4.22E-05
12:053818287	0.16	3.87E-02	9.59E-03	5.60E-05

NOTE: see the Note to Table 4.

5. DISCUSSION

We have presented efficient semiparametric inference procedures for general two-phase designs. The proposed EM algorithm is numerically stable and computationally efficient. In our analysis of the BP and LDL studies in the NHLBI ESP, it took ~10 seconds on an IBM HS21 machine to perform one association analysis. An R package that implements the proposed method is available on GitHub (https://github.com/dragontaoran/TwoPhaseReg).

Lin et al. (2013) analyzed the LDL study in the NHLBI ESP using the MLE₀ method. To avoid the dependence of the second-phase selection on the inexpensive covariates, they used the residuals instead of the original LDL values as the outcome of interest, even though the LDL values were available for all subjects. This workaround is not desirable because the resulting genetic effect estimates are difficult to interpret and not comparable with estimates from studies that use the original LDL values.

In our sieve approximation to P(X | Z), the number of interior knots b_n in the domain of Z can be chosen in a data-adaptive manner. One possible approach for choosing b_n is through cross-validation. For any fixed b_n, we use part of the data as the test set and the remainder as the validation set. We evaluate expression (2) in the validation set using estimates obtained from the test set. The optimal number of interior knots b_n is the value that maximizes the average cross-validation likelihood. Alternative approaches can also be used to choose b_n. As demonstrated in Section 4, one can use the QQ plot and genomic control λ to choose the appropriate b_n in genetic association studies.

In our sieve approximation to P(X|Z), Z cannot contain too many continuous components because of the curse of dimensionality. There are several ways to obtain a lowdimensional Z. If there is prior scientific knowledge or historical data about the dependence among covariates, then such information can be incorporated into the modeling. For example, in genetic association studies, it is often reasonable to assume that a subject’s genetic susceptibility, a factor that is determined at birth, is independent of his/her subsequent environmental exposure and age (Chatterjee and Carroll 2005). If the second-phase sample contains a random subsample (e.g., the DPR group in the NHLBI ESP), then one can test the independence between expensive and inexpensive covariates using this subsample. If such prior knowledge or data is not available, then one may adopt a dimension-reduction technique, such as principal component analysis.

We have assumed that the second-phase selection depends on a single outcome. If the selection depends on multiple outcomes in one study, then one should consider all of them simultaneously in a multivariate regression model in order to obtain valid inference. Recently, Tao et al. (2015) extended the MLE₀ approach to multivariate outcome-dependent sampling without inexpensive covariates. We can extend our SMLE approach to multivariate outcome-dependent sampling with inexpensive covariates. We simply replace P_θ(Y|X, Z, W) in expression (2) by the conditional density function P_θ(Y|X, Z, W) of the multivariate outcome Y given covariates. If Y contains missing components, then we need to modify the EM algorithm in Section 2.2 by first calculating the conditional expectations of the missing components given the observed data in the E-step and then replacing the missing components with their conditional expectations in the M-step. We expect that the asymptotic properties of our SMLEs to continue to hold.

In both the simulation studies and NHLBI ESP applications, the outcome of interest is always used in the second-phase sampling process. In practice, investigators may be interested in a secondary outcome that is not used for sampling but is correlated with the primary outcome used for sampling. In light of the above discussion on multivariate outcome-dependent sampling, it is straightforward to analyze the secondary outcome by assuming a bivariate regression model for the primary and secondary outcomes.

This work is focused on the inference procedures rather than the design aspects of two-phase studies. An important topic of investigation is the optimal study design when the primary interest is to estimate β When the outcome is continuous and there is no inexpensive covariate, Lin et al. (2013) showed that the efficient information for estimating β using the MLE₀ method is approximately Var(Y|R = 1)Var(X|R = 1)/σ⁴ (assuming that X is a scalar). This implies that the study design is more efficient if it selects subjects with more extreme values of Y. For general two-phase studies with (possibly multivariate) continuous outcomes of interest, it is unclear what the best sampling strategy is. Because our likelihood framework applies to any two-phase design, the variance estimators for the SMLE method can be used to evaluate the efficiencies of different designs.

APPENDIX: EM Algorithm

Direct maximization of expression (2) is difficult due to the intractable form of the second term. To make the problem more tractable, we artificially create a latent variable U for subjects with R = 0 such that U takes values on 1/s_n,…, 1 and satisfies the equations $P\left(U=j/s_n|Z,W\right)=B_j^q(\mathit{Z}),P\left(X={\mathit{x}}_k|Z,W,U=j/s_n\right)=P\left(\mathit{X}={\mathit{x}}_k|U=j/s_n\right)=p_{kj}$ and P(Y|X, Z, W,U) = P(Y|X, Z, W). Consequently, $P\left(X={\mathit{x}}_k|Z\right)={\displaystyle {\sum }_{j=1}^{s_n}{B}_j^q(\mathit{Z})p_{kj}}$ for subjects with R = 0, and the second term in expression (2) is equivalent to the log-likelihood of (Y_i, Z_i, W_i), assuming that the complete data consist of (Y_i, X_i, Z_i, W_i, U_i) but with both X_i and U_i missing.

We devise an EM-type algorithm to maximize expression (2) by treating (X, U) for subjects with R = 0 as missing. The complete-data log-likelihood is

$$\begin{array}{l}{\displaystyle \sum _{i=1}^n{R}_i\left\{\log P_{\theta }\left(Y_i|X_i,Z_i,W_i\right)+{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I\left(X_i={\mathit{x}}_k\right)B_j^q(Z_i)\log p_{kj}}}\right\}}\\ +{\displaystyle \sum _{i=1}^n\left(1-R_i\right)\left\{\log P_{\theta }\left(Y_i|{\mathit{X}}_i,Z_i,W_i\right)+\log P\left(X_i|U_i\right)+\log P\left(U_i|Z_i\right)\right\}}\\ ={\displaystyle \sum _{i=1}^n{R}_i}\left\{\log P_{\theta }\left(Y_i|X_i,Z_i,W_i\right)+{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I\left(X_i={\mathit{x}}_k\right)B_j^q(Z_i)\log p_{kj}}}\right\}\\ +{\displaystyle \sum _{i=1}^n\left(1-R_i\right)}\{{\displaystyle \sum _{k=1}^{m}I\left(X_i={\mathit{x}}_k\right)\log P_{\theta }\left(Y_i|{\mathit{x}}_k,Z_i,W_i\right)}\\ +{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I\left(X_i={\mathit{x}}_k,U_i=j/s_n\right)\log p_{kj}+{\displaystyle \sum _{j=1}^{s_n}I\left(U_i=j/s_n\right)B_j^q(Z_i)}}}\}.\end{array}$$

In the E-step, we calculate the conditional expectations of I(X_i = x_k,U_i = j/s_n) and I(X_i = x_k) given (Y_i, Z_i, W_i) for the ith subject with R_i = 0 as ${\widehat{\psi }}_{\mathit{kji}}=P\left(X=x_k,U=j/s_n|Z_i,W_i\right)$, and ${\widehat{q}}_{ik}={{\displaystyle {\sum }_{j^{\prime }=1}^{s_n}\widehat{\psi }}}_{k{j}^{\prime }i}\left(k=1,\dots ,m;j=1,\dots ,s_n\right)$, respectively, where

$$\begin{array}{l}P(X={\mathit{x}}_k,U=j/s_n|Y,Z,W)=\frac{P\left(X={\mathit{x}}_k,U=j/s_n,Y,Z,W\right)}{P(Y,Z,W)}\\ =\frac{P_{\theta }\left(Y|{\mathit{x}}_k,Z,W\right)B_j^q{(Z_i)}_{p_{kj}}}{{\displaystyle {\sum }_{k^{\prime }=1}^m{P}_{\theta }\left(Y_i|{\mathit{x}}_{k^{\prime }},Z_i,W_i\right){\displaystyle {\sum }_{j^{\prime }=1}^{s_n}{B}_{j^{\prime }}^q{(Z_i)}_{p_{k^{\prime }{l}^{\prime }}}}}}.\end{array}$$

In the M-step, we update θ by maximizing

$${\displaystyle \sum _{i=1}^n{R}_i\log }{P}_{\theta }(Y_i|X_i,Z_i,W_i)+{\displaystyle \sum _{i=1}^n(1-R_i){\displaystyle \sum _{k=1}^m{\widehat{q}}_{ik}\log P_{\theta }(Y_i|{\mathit{x}}_k,}{Z}_i,W_i).}$$ (A.1)

Expression (A.1) is a weighted sum of the log-likelihood functions for the regression model P_θ(Y|X, Z, W). Thus, we can use existing algorithms for weighted regression to maximize expression (A.1). We update p_kj (k = 1,…, m; j = 1,…, s_n) by maximizing

$${\displaystyle \sum _{i=1}^n{R}_i{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I\left(X_i=x_k\right)B_j^q(Z_i)\log }{p}_{kj}+{\displaystyle \sum _{i=1}^n(1-R_i)}}}{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}}}{\widehat{\psi }}_{\mathit{kji}}{\log }_{p_{kj}}$$

such that

$$p_{kj}=\frac{{\displaystyle {\sum }_{i=1}^n\left\{R_{i}I\left(X_i=x_k\right)B_j^q(Z_i)+(1-R_i){\widehat{\psi }}_{\mathit{kji}}\right\}}}{{\displaystyle {\sum }_{k=1}^m{\displaystyle {\sum }_{i=1}^n\left\{R_{i}I\left(X_i=x_k\right)B_j^q(Z_i)+(1-R_i){\widehat{\psi }}_{\mathit{kji}}\right\}}}}.$$

We start with initial values ${\widehat{\alpha }}^{(0)}=0,{\widehat{\beta }}^{(0)}=0,{\widehat{\gamma }}^{(0)}=0,{\widehat{\eta }}^{(0)}=0,{\widehat{{\sigma }^2}}^{(0)}$ being the sample variance of Y (in linear regression), and ${\widehat{p}}_{kj}^{(0)}={\displaystyle {\sum }_{i=1}^n{R}_{i}I}\left(X_i={\mathit{x}}_k\right)B_j^q(Z_i)/{{\displaystyle {\sum }_{i=1}^n{R}_i{B}_j^q(Z}}_i)$, and we iterate until convergence to obtain the SMLEs $\widehat{\theta }$ and ${\widehat{p}}_{kj}(k=1,\dots ,m;j=1,\dots ,s_n)$. Because the MLE for the distribution function of Z is the empirical distribution function based on (Z₁,…, Z_n), the joint distribution function of (X, Z), denoted by F(·,·), can be estimated by

$$\widehat{F}(\mathit{x},\mathit{z})=n^{-1}{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{i=1}^{n}I\left({\mathit{x}}_k\le \mathit{x},Z_i\le \mathit{z}\right){\displaystyle \sum _{j=1}^{s_n}{B}_j^q({\mathit{Z}}_i)}{\widehat{p}}_{kj}}}.$$ (A.2)

Remark A.1

When Z is a scalar, we can use the histogram basis ${\{B_j^1(z)\}}_{j=1}^{b_n+1}$ to estimate P(X|Z) (see Remark S.1). In this case, the artificial latent variable U is not needed, and the EM algorithm can be greatly simplified. The complete-data log-likelihood becomes

$$\begin{array}{l}{\displaystyle \sum _{i=1}^n{R}_i\left\{\log P_{\theta }\left(Y_i,|X_i,Z_i,W_i\right)+{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{j=1}^{s_n}I\left(X_i={\mathit{x}}_k\right)B_j^1(Z_i)\log p_{kj}}}\right\}}\\ +{\displaystyle \sum _{i=1}^n\left(1-R_i\right){\displaystyle \sum _{k=1}^{m}I}(X_i={\mathit{x}}_k)\left\{\log P_{\theta }(Y_i|{\mathit{x}}_k,Z_i,W_i)+{\displaystyle \sum _{j=1}^{s_n}{B}_j^1(Z_i)\log p_{kj}}\right\}}.\end{array}$$

Consequently, in the E-step, we only need to calculate ${\widehat{q}}_{ik}$ for the ith subject with R_i = 0 as

$${\widehat{q}}_{ik}={\displaystyle \sum _{j=1}^{s_n}{B}_j^1(Z_i)}\frac{P_{\theta }{\left(Y_i|{\mathit{x}}_k,Z_i,W_i\right)}_{p_{kj}}}{{{\displaystyle {\sum }_{k^{\prime }=1}^m{P}_{\theta }(Y_i|{\mathit{x}}_{k^{\prime }},Z}}_i,W_i)p_{k^{\prime }j}},k=1,\dots ,m.$$

In the M-step, we update θ by maximizing expression (A.1) and update p_kj (k = 1,…, m; j = 1,…, s_n) by the following simple formula

$$p_{kj}=\frac{{\displaystyle {\sum }_{i=1}^n\left\{R_{i}I\left(X_i={\mathit{x}}_k\right)B_j^1(Z_i)+(1-R_i)B_j^1(Z_i){\widehat{q}}_{ik}\right\}}}{{\displaystyle {\sum }_{i=1}^n{B}_j^1(Z_i)}}.$$