Resolving the Ligand Binding Specificity in c-MYC G-quadruplex DNA: Absolute Binding Free Energy Calculations and SPR Experiment

Abstract

We report the absolute binding free energy calculation and surface plasmon resonance (SPR) experiment for ligand binding with the cMYC G-quadruplex DNA. The unimolecular parallel DNA G-quadruplex formed in the nuclease hypersensitivity element III1 of the c-MYC gene promoter regulates the c-MYC transcription and is recognized as an emerging drug target for cancer therapy. Quindoline derivatives have been shown to stabilize the G-quadruplex and inhibit the c-MYC expression in cancer cells. NMR revealed two binding sites located at the 5′ and 3′ termini of the G-quadruplex. Questions about which site is more favored and the basis for the ligand-induced binding site formation remain unresolved. Here, we employ two absolute binding free energy methods, the double decoupling and the potential of mean force methods, to dissect the ligand binding specificity in the c-MYC G-quadruplex. The calculated absolute binding free energies are in general agreement with the SPR result and suggest that the quindoline has a slight preference for the 5′ site. The flanking residues around the two sites undergo significant reorganization as the ligand unbinds, which provides evidence for ligand-induced binding pocket formation. The results help interpret experimental data and inform rational design of small molecules targeting the c-MYC G-quadruplex.

Graphical abstract

INTRODUCTION

In recent years, there has been a growing interest in targeting the DNA G-quadruplex secondary structure formed in the guanine-rich regions in human telomeres and gene promoters for developing novel anti-cancer therapy^1–5. A G-quadruplex is composed of stacked planar structures (G-tetrads) formed by four hydrogen bonded guanines, with additional stabilizing forces from K⁺ or Na⁺ ions located in the central ion channel of the G-tetrad planes¹. DNA G-quadruplexes formed in the proximal location of promoters in a number of human proto-oncogenes have been found to regulate gene transcription^1,6,7, such as c-MYC^8,9, VEGF^10,11, HIF-1α¹², BCL-2^13–15, KRAS¹⁶, Rb¹⁷, c-KIT^18,19, RET²⁰, hTERT²¹, and PDGFR-β^22,23. c-MYC, one of the most commonly deregulated genes in human cancers, has a G-quadruplex-forming motif in the promoter Nuclease Hypersensitive Element (NHE) III1 which regulates 80–95% of its total transcription^8,9. The G-quadruplex formed in the c-MYC promoter region NHE III₁ is the first and most extensively studied gene promoter G-quadruplex⁹; the major G-quadruplex formed in the c-MYC promoter in K⁺ solution is a parallel-stranded structure²⁴. Parallel-stranded G-quadruplex structures are found to be common in the human promoter sequences^1,6. The G-quadruplex formed in the NHE III₁ of the c-MYC gene promoter has been recognized as a promising target for small molecule agents to modulate the transcription of c-MYC²⁵. Quindoline derivatives (Fig. 1A) have been shown to stabilize the c-MYC G-quadruplex and down-regulate the expression of c-MYC in cancer cells^26,27. The molecular structures of the c-MYC G-quadruplex and its drug complexes have been determined by solution NMR^24,28,29. New G-quadruplex-interactive ligands with micromolar activities^30–33 have been identified in recent studies using the NMR structures of apo and ligand-bound c-MYC G-quadruplex molecules.

Figure 1.

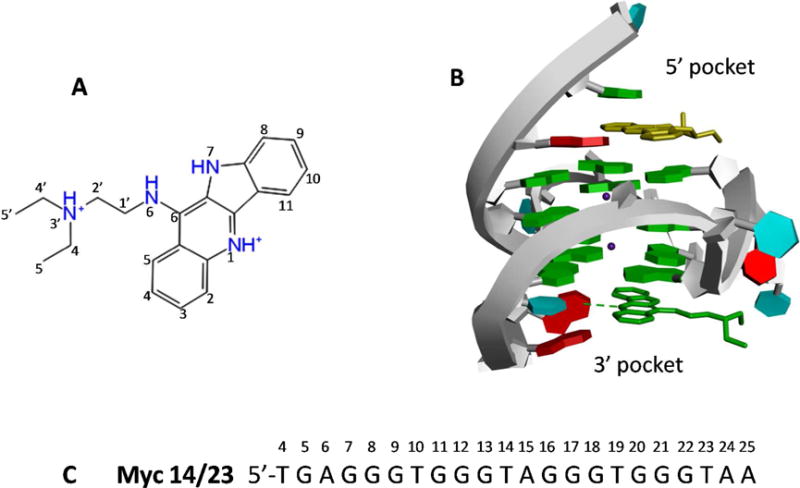
(A). The 2D structure of the quindoline derivative. (B)The NMR structure of the 2:1 quindoline-G-quadruplex complex. The two quindoline molecules at the 5′-end and 3′ end are shown in yellow and green sticks, respectively. At the 3′-end the intermolecular hydrogen bond between the T23O4 of the DNA and N1 of the quindoline is shown as green dashed line. The two potassium ions are shown as purple dots. (C). The sequence of c-MYC G-quadruplex (Myc 14/23).

Despite the progress in the discovery of new G-quadruplex-interactive ligands, important questions remain regarding the ligand-binding specificity in the c-MYC G-quadruplex. Initially, the binding mode of the quindoline with the c-MYC G-quadruplex was thought to involve a single quindoline molecule end-stacking onto the surface of the 3′-end G-tetrad²⁶. Subsequently, the NMR structure of the c-MYC G-quadruplex-quindoline complex revealed that each of the 5′- and the 3′-end binds a quindoline molecule²⁹, and that the two ligand specific binding pockets were only formed upon binding of ligands (Fig. 1B). From the structure, it is unclear which of these two sites interacts more favorably with the ligand and why. In addition, the physical reason why the two binding pockets observed in NMR²⁹ are not preformed in the free G-quadruplex²⁴ is also not well-understood. A better understanding of binding site specificity and the mechanism for the ligand-induced binding pocket formation will assist in the interpretation of experimental data and inform on rational design of more potent c-MYC G-quadruplex-interactive small molecules.

Experimentally, equilibrium binding constants can be determined by methods such as surface plasmon resonance (SPR) and isothermal titration calorimetry (ITC). However, these methods cannot directly measure ligands binding affinities at different binding sites. Although site-specific binding parameters may be extracted by various fitting methods, the reliability of such procedures is low for different binding affinities at different binding sites unless these binding affinities are significantly different. More importantly, even when the individual binding constants can be extracted from model fitting, they cannot be assigned to the specific binding sites by these methods alone. While NMR spectroscopy can provide important structural information on binding-site conformation^29,31, it does not directly provide accurate measurement of binding affinities for individual binding sites, nor does it provide quantitative mechanistic information for binding specificity and affinity.

To gain atomistic insights into the binding site specificity in the c-MYC G-quadruplex, here we employ two absolute binding free energy methods^34–37, the potential of mean force method (PMF)^38–41 and double decoupling method (DDM)^42–44, on the quindoline compound used in the NMR structural study^26,29 to compute the intrinsic binding affinities for each binding site in the c-MYC G-quadruplex. In recent years, statistical mechanics based absolute binding free energy methods such as DDM^42–44 have increasingly been applied to compute protein-small molecule binding free energy^45–50, and we and others have shown that such methods can generate more accurate results compared with the more rapid docking and MM-PB(GB)/SA in estimating binding affinity for a number of protein-ligand systems^51–53. However, the DDM method has not yet been applied to small molecule-DNA (or RNA) complexes. A DDM calculation of ligand-DNA binding will involve decoupling the ligand from the ionic solution containing the flexible and highly charged DNA. Such calculations can be computationally challenging for charged ligands because of the large magnitude of their electrostatic decoupling free energies^38,40,54 Here, we apply DDM for the first time to compute the absolute binding free energy for a ligand-nucleic acid system, taking into account the electrostatic corrections for the effects of the finite-size periodic simulation system on the electrostatic free energy.⁵⁴ We also employ the PMF method to study the binding thermodynamics of the quindoline-c-MYC G-quadruplex complex, using a new formula for the absolute binding free energy (see Methods). The PMF approach has a distinct advantage in computing the absolute binding free energy of charged ligand in that it uses a physical pathway to move the ligand out of the binding site, rather than alchemically decouples the charged ligand from the ionic solution.^38,47,55,56 Using two different absolute binding free energy methods with the same energy function can cross validate the internal consistency of the computational results. We have also experimentally determined the apparent binding constant of quindoline binding to the c-MYC G-quadruplex using SPR, by assuming that the two binding sites have the same binding affinity.

We find that the calculated absolute binding free energies of the quindoline molecule for the two binding sites are in general agreement with the SPR-derived overall binding free energy to within ~2 kcal/mol. The calculated equilibrium binding constant is also compatible with the IC₅₀ of inhibition by this compound. Both the PMF and DDM calculations suggest that the quindoline compound has a slight preference for the 5′-end pocket of the G-quadruplex; this is consistent with the NMR spectral of the flanking residues forming the two binding sites. The DDM calculations indicate that the difference between the affinities of the 5′ and 3′ sites is mainly attributable to the favorable nonpolar interaction between the planar quindoline core and the 5′ binding cavity. In contrast, the electrostatic interactions are found to actually favor the 3′ binding, which is consistent with the NMR data showing that the 3′-end binding is ionic concentration-dependent²⁹. The simulations also reveal significant conformational rearrangements in the 5′-end and 3′-end flanking residues as the ligands unbind, which eventually causes the instability of the binding pockets in the apo G-quadruplex. This result supports the notion that the binding pockets in the c-MYC G-quadruplex are induced by ligand binding²⁹. To understand the instability of the binding pocket in the apo G-quadruplex, we computed the energetics of the water molecules occupying the unliganded 5′- and 3′ cavities using the Hydration Site Analysis (HSA)^57,58 and found that unfavorable hydration and poor solute-water interactions contribute to the instability of these pockets and promote ligand binding. These insights into the binding site specificity may help inform the discovery and optimization of small molecules targeting the c-MYC G-quadruplex.

MATERIALS AND METHODS

Determination of Equilibrium Dissociation Constant K_d from SPR

The SPR measurements were performed with a four-channel BIAcore 2000 optical biosensor system (GE Healthcare). The oligonucleotide 5′-Biotin-d[T₅TGAG₃TG₃TAG₃TG₃TA₂] (Myc 14/23) was purchased from Sigma-Aldrich (Woodlands, TX). 5′-Biotin labeled DNA was immobilized onto streptavidin coated sensor chips (SA chip from BIAcore, GE Healthcare) by injection of DNA stock solution at 10 μg/ml with a flow rate of 10 μl/min for 30 minutes. One flow cell was used to immobilize the DNA oligomer sample, while an additional cell was left blank as a control. The total response unit (RU) for Myc 14/23 was 2193. The SPR experiments were performed at 25°C in filtered (0.22 μm) and degassed 10 mM HEPES buffer (pH 7.4) containing 100 mM KCl, 3 mM EDTA and 0.005% surfactant Polysorbate 20. Quindoline drug solutions (0.1, 0.2, 0.5, 1, 5, and 10 μM) were prepared by serial dilutions from stock solution and injected from 7 mm plastic vials with pierceable plastic crimp caps. Solutions of various drug concentrations were injected through the flow cells until a constant steady state response was obtained. Drug solution flow was then replaced by buffer flow resulting in dissociation of the complex. In general, a series of different drug concentrations were injected onto the chip with a flow rate of 30 μl/min for a period of 5 minutes followed by a dissociation period of 7 minutes. After each cycle, the chip surface was regenerated with 30 seconds injection of pH 2.5 glycine solution and multiple 1 minute buffer injections. The reference response from the blank cell was subtracted from the response in each cell containing DNA to give a signal (RU) that was directly proportional to the amount of bound compound. A set of sensorgrams at different concentrations for binding of quindoline to DNA was obtained. The equilibrium constant was obtained from the fitting plots of RU versus free drug concentration. The equilibrium dissociation constant (K_d) was obtained using the 1:1 Langmuir binding model. The association (k_on) and dissociation (k_off) rate constants were fitted simultaneously using the following equation:

$$\text{dR}/\text{dt}={\mathrm{k}}_{\text{on}}\mathrm{C}({\mathrm{R}}_{max}-\mathrm{R})-{\mathrm{k}}_{\text{off}}\mathrm{R}$$

where R represents the response unit, C is the concentration of quindoline. The experiments were done in triplicate.

Molecular dynamics simulation setup

The starting structure for the molecular dynamics simulations is the solution NMR structure of the 2:1 quindoline-c-MYC G-quadruplex (PDB entry 2L7V, Fig. 1B)²⁹. The G-rich sequence (Myc 14/23) used in the NMR structure determination is the modified wild-type sequence with two G-to-T substitutions at the 14 and 23 positions (Fig. 1C). This sequence has been shown to adopt the single predominant c-MYC promoter G-quadruplex in K⁺ solution and whose apo- and ligand bound structures were determined by NMR^24,29. The 5′-flanking segment of the Myc 14/23 sequence is the same as that in the wild-type sequence. The T23 of the 3′-flanking segment TAA is a mutation from the wild-type G23 of the corresponding 3′-flanking GAA segment. As shown previously²⁴, both the mutant TAA and wild-type GAA 3′-flanking segments can form similar stable fold-back conformations. In this study, all the MD simulations were started from the first structure of the NMR ensemble, since the difference among the 10 structures in the NMR ensemble is small: the RMS deviations between structure 1 and all the rest of the structures in the NMR ensemble are below 1 Å, comparing with the average RMS fluctuation of ~ 2 Å observed in the MD simulation of the G-quadruplex. Before running the free energy simulations, we determine the pKa of the N1 atom of the quindoline to be ≈ 10.2 (Fig. 1A) using the QM Jaguar pKa program⁵⁹. Therefore, at physiological pH, the N1 site is treated as protonated in the simulations.

In this work, the MD binding free energy simulations using the PMF and DDM approaches were performed using the GROMACS 4.6.4⁶⁰. The AMBER parmbsc0 force field⁶¹ is used to model the c-MYC G-quadruplex DNA in aqueous solutions. We have also performed MD simulations on the quindoline-cMYC G-quadruplex complex using the AMBER parmbsc1 force field⁶². Starting from the NMR structure of the complex, the ligand binding pockets are severely distorted in these simulations using the parmbsc1 force field. By contrast, the two ligand binding pockets remain stable in the MD simulations run with the parmbsc0 force field. Therefore, all the free energy simulations were carried out using the parmbsc0 force field. The quindoline ligand is modeled by the Amber GAFF parameters set⁶³ and the AM1-BCC charge model⁶⁴. A truncated octahedral box containing TIP3P water ⁶⁵ olecules previously equilibrated at 300 K and 1 atm pressure was used to solvate the quindoline-DNA complex. The dimension of the solvent box is set up to ensure that the distance between solute atoms from nearest walls of the box is at least 10 Å. K⁺ ions are added to the solvent box to maintain charge neutrality. The Lennard-Jones parameters developed by Joung and Cheatham are used to model the K⁺ metal ion⁶⁶. A recent report shows that with the use of the Åqvist parameter⁶⁷ for K⁺ the K+ ions in the central ion channel of the G-tetrads can escape from the G-quadruplex, while such channel ion escape was not observed with the use of the Joung and Cheatham parameter⁶⁸. The electrostatic interactions were computed using the particle-mesh Ewald (PME) method ⁶⁹ with a real space cutoff of 10 Å and a grid spacing of 1.0 Å. MD simulations were performed in the NPT ensemble with a time step of 2 fs.

Using the PMF approach to calculate absolute binding free energy

The PMF method^38,39,70 uses a physical pathway connecting the bound and unbound states to compute the absolute binding free energy. We have derived a new formulation for the absolute binding free energy expression in the PMF approach: see Eq. (1), whose derivation is given in the Supporting Information. The computation of the $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ involves the following steps: (1) apply harmonic restraint on the three Euler angles (Fig. S1) of the ligand in the bound state to restrain ligand orientation; (2) apply harmonic restraint on the polar and azimuth angles (Fig. S1) in the spherical coordinates to restrain the ligand center along a fixed axis when it binds/unbinds; (3) reversibly remove the ligand from the binding pocket along the chosen axis until it reaches the bulk region; (4) compute the free energy change when the restraints on the ligand center and ligand orientation are removed and the ligand is allowed to occupy the standard volume 1/C° and rotate freely in the bulk region. The corresponding expression for the absolute binding free energy is

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{°}=-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bound}}-w(r^{\ast })-k_{B}T\ln \frac{{\displaystyle {\int }_{\mathit{bound}}{e}^{-w(r)/k_{B}T}dr}}{{(2\pi k_{B}T/k_r)}^{\frac{1}{2}}}+\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bulk}}$$ (1)

Here $-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bound}}$ is the free energy of restraining the ligand orientation in the bound state; w(r) is the reversible work (potential of mean force or PMF) of pulling the ligand center away from the binding site to the current location r. r* is an arbitrary location of the ligand center in the bulk region. The computed value of $\mathrm{\Delta }{G}_{\mathit{bind}}^{°}$ does not depends on the choice of the bulk location r*⁴⁰. ${\displaystyle {\int }_{\mathit{bound}}{e}^{-w(r)/k_{B}T}}dr$ is a 1D line integral which spans the entire region corresponding to the bound state. k_r is the force constant of the harmonic restraint which constrains the ligand to be in the proximity of the bulk location r*. $\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bulk}}$ is the free energy of applying the positional and orientational restraints on the ligand in the bulk solvent. The complete derivation and details of the PMF calculation are given in the SI.

Using the DDM to dissect absolute binding free energy into physically meaningful terms

In order to understand the molecular driving force underlying the binding site selectivity, we also performed DDM calculation^42–44,46, which can decompose the absolute binding free energy $\mathrm{\Delta }{G}_{\mathit{bind}}^{°}$ into contributions from electrostatic and nonpolar interactions (Supporting Information). The calculation involves two legs of alchemical decoupling simulations, in which a spatially restrained ligand is decoupled from the receptor binding pocket or from the bulk solution by gradually turning off the nonbond interactions (first Coulomb interaction and then the Lennard-Jones interaction) between the ligand and its environment. The absolute binding free energy $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ can be written as

$$\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}=-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{coupled}}+\mathrm{\Delta }{G}_{\mathit{Coulomb}}+\mathrm{\Delta }{G}_{LJ}+\mathrm{\Delta }{G}_{\mathit{elec}\_\mathit{corr}}^{\mathit{finite}\_\mathit{size}}+\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{gas}}$$ (2)

where ΔG_Coulomb and ΔG_LJ can be interpreted as the contributions of the effective electrostatic interactions and the nonpolar interactions to the total binding free energy, respectively^46,71. The term $\mathrm{\Delta }{G}_{\mathit{elec}\_\mathit{corr}}^{\mathit{finite}\_\mathit{size}}$ is the correction that accounts for the effects of finite-size, periodic simulation system on the calculated electrostatic free energy of decoupling a charged ligand. Here, $\mathrm{\Delta }{G}_{\mathit{elec}\_\mathit{corr}}^{\mathit{finite}\_\mathit{size}}$ is estimated using a scheme developed by Rocklin and coworkers.⁵⁴ The remaining terms $\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{coupled}}$ and $\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{gas}}$ are the free energy of spatially restraining the ligand to remain in the binding site for a fully coupled ligand and that for a fully decoupled ligand, respectively (see Supporting Information for more details of the DDM and its binding free energy decomposition scheme).

Hydration Sites Analysis

To understand the origin of the instability of the binding pocket in the apo G-quadruplex, we performed Hydration Sites Analysis (HSA)^58,72 to compute the energetics of the water molecules occupying the unliganded 5′- and 3′ cavities. The HSA calculations involved three steps: (1) molecular dynamics simulations to generate water molecule distributions in the binding cavity, (2) cluster analysis of these water molecule distributions to isolate high density regions of water molecules (i.e. hydration sites) and (3) energy calculations of the hydration sites using inhomogeneous solvation theory. Additional structural properties such as enclosure of the hydration site and hydrogen bonds to water molecules in the hydration site allow for a more complete understanding of the solvation properties of these two cavities. In this work, we performed HSA analysis on a subset of 10,000 frames from a 100 ns production trajectory. High density spherical regions (hydration sites) of 1Å radius were identified using a clustering procedure⁵⁸ on the water molecules that were found within 3 Å of the heavy atoms of the quindoline rings in an aligned holo conformation. The resulting hydration sites were each populated by retrieving all water molecules, which had oxygen atoms within 1.0 Å from the corresponding hydration site center. The hydration sites were then enumerated according to their occupancies, with the highest populated site given the index 0.

The energy of each hydration site (E_total) is calculated as a function of the pairwise solute-water energies (E_sw) and water-water energies (E_ww)⁵⁸,

$$E_{\mathit{tot}}=\frac{1}{2}(E_{sw}+E_{ww})$$

where a factor of one-half takes into account the assignment of pairwise interactions to each molecule in the pair.

Hydrogen bonds were identified based on the following geometric criteria: the donor–acceptor heavy atom distance is less than or equal to 3.5 Å and the hydrogen–donor–acceptor angle is less than or equal to 30°⁷². The total number of hydrogen (HB_tot) is equal to sum of the solute-water (HBsw) and water-water hydrogen bonds (HBww).

Fractional enclosure (f_enc) was calculated based on the following function:⁷²

$$f_{\mathit{enc}}=1-\frac{N_{\mathit{nbr}}}{N_{\mathit{nbr}-\mathit{bulk}}}$$

where N_nbr is mean number of water molecules found in the first hydration shell of a hydration site or first shell neighbors and N_nbr-bulk is mean number of first-shell neighbors of a TIP3P water molecule in neat water simulation as defined in this previous work. This quantity indicates the degree to which the water in a hydration site is blocked from contact with other water molecules.

More details of the MD simulations used to perform the HSA are given in the Supporting Information.

RESULTS

Binding affinity determined by SPR measurements indicates that quindoline binds the c-MYC G-quadruplex tightly with a slow k_on

SPR is used to experimentally determine the equilibrium binding constant K_a of quindoline to Myc 14/23 d[TGAG₃TG₃TAG₃TG₃TA₂]^24,29 from the direct measurements of complex association (k_on) and dissociation (k_off) rates in real time. Biotinylated oligonucleotide was immobilized on a streptavidin-coated sensor chip. Increasing concentrations of quindoline (0.1, 0.2, 0.5, 1, 5, and 10 μM) were injected and the interaction of the quindoline with the oligonucleotides was measured. Binding between quindoline and MycG4 was observed at quindoline concentration as low as 0.1 μM (Fig. 2). The intensity of the observed response increased with increasing concentrations of quindoline in a dose dependent manner. By fitting the sensorgrams using a 1:1 Langmuir model, the association constant K_a for Myc 14/23 was calculated as 3.27×10⁶M⁻¹. Directly measured k_on and k_off are 2.57×10⁴ ± 140 M⁻¹ s⁻¹ and 7.87×10⁻³ ± 2.91×10⁻⁵ s⁻¹, respectively (Table 1). It should be noted that the on-rate k_on is much slower than the diffusion-limited on-rate for bimolecular binding, which is on the order of ~10⁹ M⁻¹ s⁻¹. The slow binding of quindoline to the c-MYC G-quadruplex is likely to reflect the ligand-induced conformational rearrangement near the binding sites, as shown by computation simulations described later.

Figure 2.

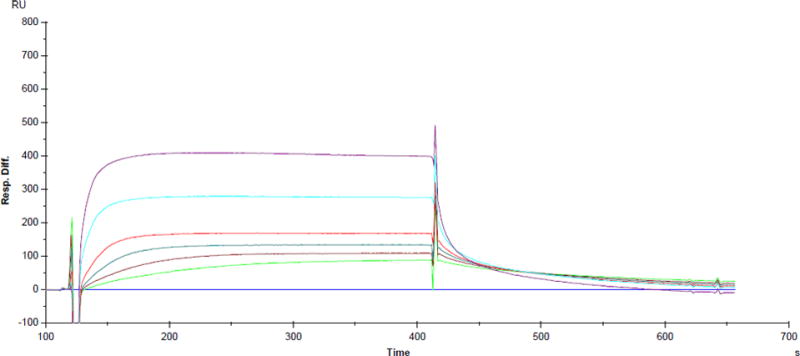
SPR sensorgram for binding of increasing concentrations of quindoline to Myc 14/23 d[TGAG₃TG₃TAG₃TG₃TA₂] in 10mM Hepes, 100mM KCl, 3mM EDTA, 0.005% Polysorbate 20, pH 7.4. The concentrations of quindoline are 0.1, 0.2, 0.5, 1, 5, and 10 μM.

Table 1.

Binding kinetic and thermodynamic parameters from SPR.

kon (M−1 s−1)	koff (s−1)	Ka (M−1)	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}{(\text{kcal}/\text{mol})}^{\mathrm{a}}$
2.57×104 ± 140	7.87×10−3 ± 2.91×10−5	3.27×106 ± 3.0×104	−8.94 ± 0.005

^a $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}=-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\times \ln {\mathrm{K}}_{\mathrm{a}}$.

Absolute binding free energies for the two binding sites from PMF approach suggest that the quindoline binds the 5′ end with a slightly higher affinity

Using the NMR structure of the 2:1 quindoline-c-MYC G-quadruplex²⁹ (Fig. 1B) as the starting point for MD simulation, we computed the absolute binding free energies $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ for quindoline molecules bound at the 5′ and 3′ sites: see Table 2.

Table 2.

Absolute binding free energies of the quindoline at the two binding sites from computation and experiment. (in kcal/mol.)

Binding Site	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ PMF approach	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ DDM, no-ligand-intramoleculara	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ DDM, with-ligand-intramolecularb	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ Experimentc
5′-end	−8.8 (±0.6)	−11.2 (±1.3)	−12.4 (±1.7)	−8.94
3′-end	−7.7 (±0.7)	−9.6 (±0.6)	−7.5 (±0.3)

^aThe intramolecular nonbonded interactions in the decoupled ligand are turned off.

^bThe intramolecular interactions in the decoupled state of the ligand are left unchanged.

^cDerived from SPR.

The $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ calculated from the PMF for the 5′ and 3′ binding sites are −8.8 (±0.6) kcal/mol and −7.7 (±0.7) kcal/mol respectively, in good agreement with the effective $\mathrm{\Delta }{G}_{\mathit{bind}}^{°}$ of −8.94 kcal/mol determined from SPR. The agreement with the experiment supports the free energy model used in this study and allows us to further analyze the binding site specificity in the c-MYC G-quadruplex.

The calculated binding free energies shown in Table 2 suggest that the quindoline compound has a slight preference for the 5′ pocket. Later on we will compare this result with previous NMR results and with the DDM calculations. To gain insights into the nature of the quindoline binding at the two sites, we examine the different free energy contributions in the PMF calculation of $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ (Table 3). These include: $\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bulk}}$, the free energy associated with restraining the position and orientation of the ligand to a bulk location r*; −w(r*), the reversible work of physically moving the orientationally restrained ligand from the bulk into the center of the binding site; and $-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bound}}$ the free energy of releasing all the restraints in the bound state. Table 3 shows that all these three terms make important contributions to the final $\mathrm{\Delta }{G}_{\mathit{bind}}^{°}$; the highly attractive PMF term −w(r*) is largely offset by $\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bulk}}$, the free energy cost of spatially and orientationally restraining the unbound ligand to the bulk location.

Table 3.

Contributions to the absolute binding free energy $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ calculated using the PMF approach.^a (in kcal/mol.)

Binding free energy components	5′ site	3′ site
—w(r*)	−15.1 (±0.5)	−12.8 (±0.8)
$-k_{B}T\ln \frac{{\displaystyle {\int }_{\mathit{bound}}{e}^{-w(r)/k_{B}T}dr}}{{(2\pi k_{B}T/k_r)}^{\frac{1}{2}}}$	−0.1 (±0.05)	−0.0 (±0.0)
$\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bulk}}$	10.1 (±0.0)	9.4 (±0.0)
$-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{bound}}$	−3.7 (±0.06)	−4.3 (±0.05)
$\mathrm{\Delta }{G}_{\mathit{bind}}^{°}$	−8.8 (±0.6)	−7.7 (±0.7)

^aSee Methods for the definition of the different binding free energy components.

PMF results show that both binding pockets at the 5′- and 3′-ends undergo significant rearrangement as the ligand unbinds

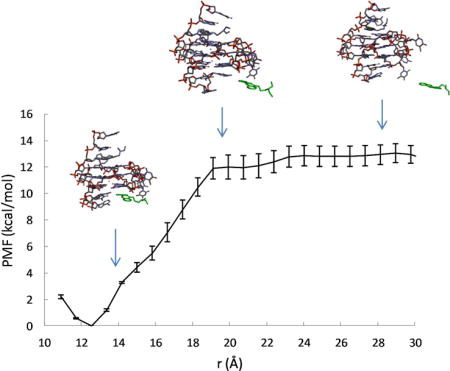
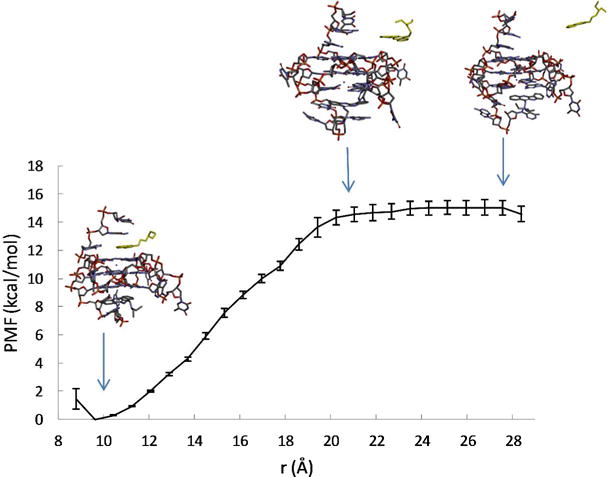
To investigate the effect of ligand binding on the conformation and dynamics of the G-quadruplex, we examine the intermediate structures of the ligand-DNA complex observed as the ligand is pulled out of the binding pocket, together with the calculated free energy profile w(r) as a function of the ligandbinding site distance r (see Fig. 3 and Fig. 4). The w(r) curves measure the energy expended to pull the ligand out of the binding pocket. For both binding sites, the free energy minimum in w(r) coincides with the ligand-binding site distance found in the NMR structure of the quindoline-DNA complex²⁹. From the free energy minimum, the w(r) increases steadily as the ligand leaves the binding pocket; the curve levels off after a characteristic distance (≈ 19 Å for the 3′ pocket, and ≈ 20 Å for the 5′ pocket), where the quindoline fused ring completely loses its stacking interaction with the terminal G-tetrads and enters the bulk solution.

Figure 3.

Calculated free energy profile w(r) for the 5′ quindoline of as a function of the distance r between the ligand atom A and the DNA atom a. The representative conformations of the G-quadruplex-quindoline complex observed at different r are also shown, with the quindoline molecule represented by yellow sticks.

Figure 4.

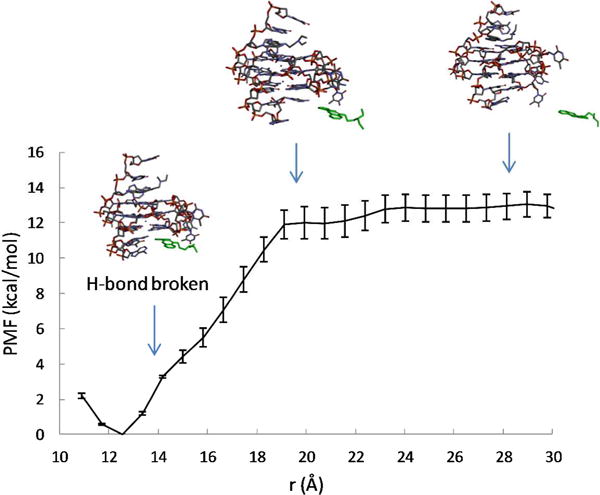
Calculated free energy profile w(r) for the 3′ quindoline. The representative conformations of the G-quadruplex-quindoline complex observed at the different r are also shown, with the quindoline molecule represented as green sticks.

An important observation from the structures along the ligand unbinding pathway is that both binding pockets undergo significant rearrangement as the ligand unbinds (Fig. 5). For the 5′ binding pocket, in the ligand bound structure (Fig. 5A), the flanking bases of G5, A6 and the 5′-end G-tetrad together form a concave binding pocket, which enables the base ring of G5 to stack over and wrap around the plane of the quindoline fused ring; as the ligand unbinds from the 5′ pocket (r > 20 Å), the 5′ flanking residues undergo large fluctuations and adopt a variety of structures. Fig. 5B and Fig. 5C show two representative arrangements in which the drug-induced binding pocket at the 5′-end collapses after unbinding of the ligand. In Fig. 5B, the G5 base ring stacks over the A6; in Fig. 5C, the base rings of both G5 and A6 stack on the 5′ end G-tetrad plane. The collapse of the binding cavity caused by ligand unbinding observed here from MD simulation is consistent with the NMR structures of the free c-MYC G-quadruplex and its quindoline complexes: in the complex structures the 5′ binding pocket only exists in the ligand bound DNA G-quadruplex due to the ligand-induced orientation of the flanking bases of G5 and A6^24,29. Significant conformational change of the flanking residues due to ligand unbinding is also seen in the simulated structures of the 3′ pocket: as seen from the Fig. 5D, in the ligand-bound state, the A25 base ring is at an angle of 60° relative to the T23 base; as the ligand unbinds, the base ring of A25 becomes coplanar with respect to that of T23: see Fig. 5E and 5F. Comparing the NMR structures of the apo and ligand-bound G-quadruplex^24,29, we find similar conformational rearrangements at the 3′-end. Therefore, it appears that the MD simulations used to compute PMF capture the key conformational reorganization in the two binding pockets. It should be noted that the free energy change associated with ligand induced binding pocket reorganization is an important component of the absolute binding free energy. This free energy of reorganization is implicitly contained in the PMF function w(r). To understand how w(r) implicitly contains the information of the receptor binding site reorganization, we consider for example what happens to the w(r) during the collapse of the 5′ pocket upon ligand unbinding: when the ligand is about to leave the binding pocket, suppose that the pocket residues are rigid, then the ligand will still experience the remaining attractive forces which will cause the w(r) to continue to rise; in reality however, as the ligand is about to leave the pocket the pocket will undergo conformational change that will “push” the ligand out such that the pocket will reach the collapsed state as soon as the ligand is completely out. This tendency of the ligand being “pushed out” by the pocket when the ligand is about to leave the pocket helps cancel out some of the remaining attractive forces from the pocket and effectively lowers the PMF w(r). It should be noted that while this free energy of the pocket reorganization is accounted for here by the PMF function w(r) generated by MD, such receptor reorganization effects are difficult to be treated properly using the more rapid methods such as docking or MM-PB(GB)/SA⁵³.

Figure 5.

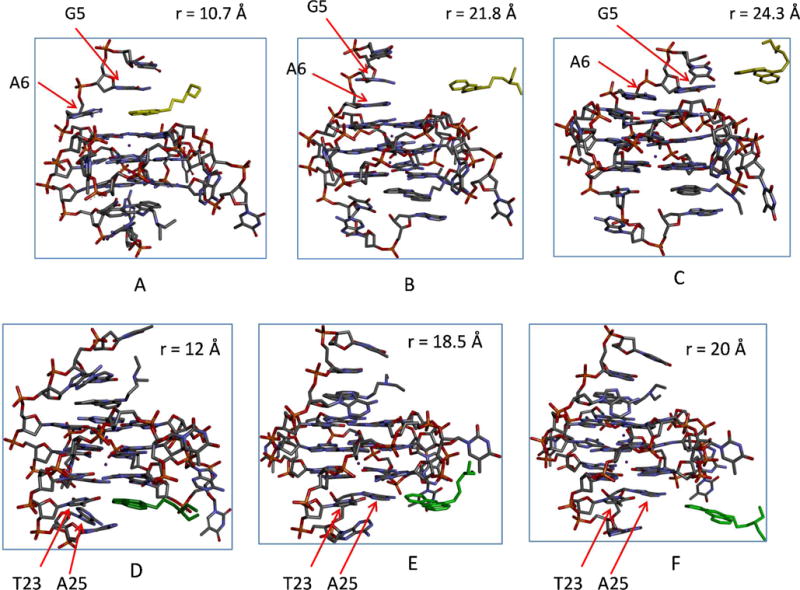
(A), (B) and (C): conformational changes near the 5′-end pocket induced by ligand unbinding with increasing ligand-DNA distance. (D), (E), and (F): conformational changes near the 3′-end site induced by the ligand unbinding at different ligand-DNA distances.

PMF results reveal differences in the 5′ and 3′ complexes

Comparisons of the PMF curves shown in Figures 3 and Fig. 4 reveal that, while the increase in w(r) for the 5′ complex is smooth, the corresponding w(r) for the 3′ complex suggests a two-step process: starting from the free energy minimum at r = 12.6 Å, w(r) rises relatively sharply within a short range from r = 12.6 Å to 14.2 Å, which corresponds to the breaking of the intermolecular hydrogen bond between the protonated N1 of the quindoline and O4 atom of the base of the flanking T23 at the 3′-end (Fig. 4; see also Fig. S2 in the Supporting Information); thereafter w(r) rises somewhat less rapidly, which reflects the gradual loss of the quindoline ring stacking with the 3′-end G-tetrad plane with increasing r. The direct contribution of the intermolecular H-bond between the quindoline-N1 and T23-O4 to the binding free energy of the 3′ complex is therefore estimated to be ~ −4 kcal/mol. By comparison, no intermolecular H-bond is formed in the 5′ complex, and the rise in the w(r) is attributable to the loss of the hydrophobic enclosure of the quindoline ring in the 5′ pocket formed by the 5′-end G-tetrad plane and the flanking G5 base (Fig. 3 and Fig. 5A). While the intermolecular hydrogen bond formation in the 3′ complex was suggested by NMR structural study²⁹, it was not directly observed in NMR experiments; the result from the PMF calculations confirms the differences between the 5′ and 3′ complexes and the intermolecular hydrogen bond formation between quindoline and the 3′ end DNA.

Decomposition of absolute binding free energy into physically meaningful contributions by DDM

To understand the physical reasons for the difference in the binding affinities of quindoline at the two binding sites (Table 2), we decompose the absolute binding free energy into physically meaningful components using the DDM method⁷¹. In this work, we used two different DDM setups involving different thermodynamic states for the fully decoupled ligand to compute $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$. We first discuss the results obtained using the DDM setup in which all the intramolecular nonbonded interactions are turned off in the decoupled ligand (i.e. as the ligand is decoupled intermolecularly from the environment, its intramolecular noncovalent interaction is also turned off). The calculated $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ for the 5′-end and 3′- end complexes are −11.2 (±1.3) kcal/mol and −9.6 (±0.6) kcal/mol, respectively (Table 2). This result is in general agreement with the experimental $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ of −8.94 kcal/mol to within ~ 2 kcal/mol. Consistent with the binding free energies estimated from PMF, the $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ calculated using this DDM setup also suggests that the quindoline binding at the 5′ site is somewhat stronger than that at the 3′ site.

Next, we examine the contributions to the $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ computed by DDM. In DDM, the $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ is obtained as the sum of several terms including the effective nonpolar free energy contribution δG_LJ and the effective electrostatic free energy contribution δG_Coulomb (see Methods). Table 4 shows the free energy decompositions obtained using the DDM setup in which the nonbonded intramolecular interactions in the decoupled ligand are turned off. The difference in the electrostatic free energy contributions ΔG_Coulomb actually favors the binding at the 3′-end by about −1.7 kcal/mol, which likely reflects the QuiN1H-T23O4 intermolecular hydrogen bond present at the 3′ site (Fig. 1B, Ref²⁹). However, the more favorable ΔG_Coulomb is outweighed by the larger difference in the nonpolar free energy contribution δG_LJ which favors the binding at the 5′ site by about −3.3 kcal/mol; the net result is that the 5′ complex is more stable than the 3′ complex by about −1.6 kcal/mol. Table 4 also shows that the corrections for the effect of the finite-size periodic simulation system on the electrostatic free energy are on the order of ~0.8 kcal/mol.

Table 4.

Contributions to the binding free energy from DDM with the nonbonded intramolecular interactions in the decoupled ligand turned off.^a (in kcal/mol.)

Binding Site	ΔGCoulomb	ΔGLJ	$\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{gas}}$	$\mathrm{\Delta }{G}_{\mathit{elec}\_\mathit{corr}}^{\mathit{finite}\_\mathit{size}}$	$-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{coupled}}$	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$
5′-end	1.2 (±0.8)	−14.7 (±1.4)	3.2 (±0)	−0.79 (±0.1)	−0.07 (±0.01)	−11.2 (±1.3)
3′-end	−0.5 (±1.7)	−11.4 (±1.1)	3.2 (±0)	−0.81(±0.03)	−0.12 (±0.05)	−9.6 (±0.6)

^aSee Methods for the definition of different binding free energy terms.

We have also computed binding free energies using a DDM setup in which the ligand intramolecular nonbonded interaction is left unchanged when the ligand is decoupled intermolecularly from its environment (Table 2 and Table 5). Here, the estimated $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ for the binding at the 5′-end and 3′-end are −12.4 (±1.7) kcal/mol and −7.5 (±0.3) kcal/mol, respectively, which deviate from the experimental $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ = −8.94 kcal/mol by 1.5–3.5 kcal/mol. This DDM result also shows that the quindoline binding at the 5′-end is stronger than that at the 3′-end. Qualitatively similar results on the relative importance of the electrostatic contribution ΔG_Coulomb and nonpolar contribution ΔG_LJ are also obtained (Table 5).

Table 5.

Contributions to the binding free energy from the DDM setup in which the nonbonded intramolecular interactions in the decoupled ligand are not scaled. (in kcal/mol.)

Binding Site	ΔGCoulomb	ΔGLJ	$\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{gas}}$	$\mathrm{\Delta }{G}_{\mathit{elec}\_\mathit{corr}}^{\mathit{finite}\_\mathit{size}}$	$-\mathrm{\Delta }{G}_{\mathit{restr}}^{\mathit{coupled}}$	$\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$
5′-end	−1.6 (±0.4)	−13.5 (±1.4)	3.2 (±0.0)	−0.36 (±0.07)	−0.09 (±0.03)	−12.4 (±1.7)
3′-end	−1.0 (±0.5)	−8.7 (±0.7)	3.2 (±0.0)	−0.89 (±0.04)	−0.12 (±0.04)	−7.5 (±0.3)

The slight preference of quindoline for the 5′ site is likely related to its greater hydrophobic enclosure

As seen in Table 4 and Table 5, the difference in the binding free energy $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ for the 5′ and 3′ sites is dominated by δG_LJ. This term reflects the effective nonpolar interaction between the ligand and the DNA binding site, which includes contributions from several thermodynamic processes, including the desolvation of the ligand from the bulk solvent, the displacement of the binding cavity water molecules by the ligand, and the direct intermolecular Lennard-Jones interactions. To understand qualitatively why the effective nonpolar ligand-DNA interaction is stronger at the 5′ site, we examine the difference in the geometries of the two binding pockets (Fig. 6). At the 5′ end the flanking residues G5 and A6 and the 5′-end G-tetrad arrange themselves to form the cavity which wraps around the quindoline ring, which results in an intercalation type of binding. Binding interfaces displaying such hydrophobic enclosure characters are known to contribute additional affinity to binding⁷³, because (a) the enclosed ligand interact with receptor atoms on both sides of the binding cavity and (b) the water molecules occupying the unliganded cavity are thermodynamically less stable since they cannot form extensive hydrogen bonds with the neighboring water molecules or solute⁵⁷. Importantly, comparing with the 5′ cavity, the extent of hydrophobic enclosure in the 3′ cavity is more limited (Fig. 6). The magnitude of the effect of hydrophobic enclosure to binding free energy can be estimated using a simple surface area model: from Fig. 6, the 5′ pocket has a larger buried van der Waals surface area than that at the 3′ site by ΔA ≈ 26 Ų; Using a surface tension coefficient γ = 0.072 kcal mol⁻¹ Ų in the surface area model for binding free energy, ΔG = − γΔA^74,75, the hydrophobic enclosure would favor the binding at the 5′ site by −1.8 kcal/mol. This value is understandably smaller than the difference of −3.3 kcal/mol in the effective nonpolar contribution ΔG_LJ estimated from DDM, since ΔG_LJ also includes the contribution from direct intermolecular Lennard-Jones interactions, which also favors the binding at the 5′ site. The above analysis suggests that residue G5 is crucial for ligand binding at the 5′ site (Fig. 6). Importantly, the critical role played by the G5 in the specific binding of quindoline was borne out by the experimental mutational analysis, which shows that the G-to-T mutation at position 5 markedly weakened the quindoline binding²⁹. In contrast, the quindoline binding at the 3′-end relies less on capping interactions as shown by mutational analysis²⁹.

Figure 6.

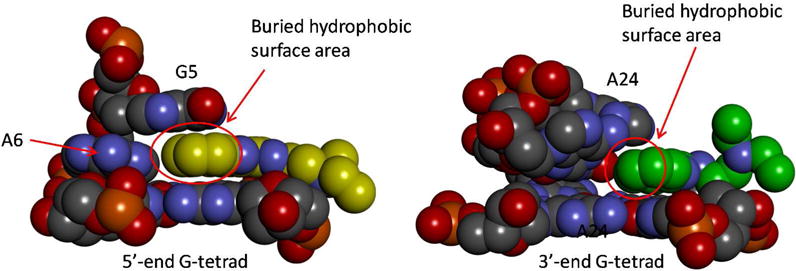
Detailed views of the 5′-end (left) and 3′-end (right) binding pockets. The carbon atoms in the two quindolines are displayed as yellow (left) and green (right) spheres. The red circles indicate the buried hydrophobic surface areas in each of the binding sites.

The results shown in Table 4 and Table 5 indicate that the errors in the $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ calculated using the DDM setup without turning off intramolecular nonbonded interactions in the decoupled ligand are larger than those obtained with the intramolecular nonbonded interactions turned off in the decoupled ligand. The larger absolute error in the $\mathrm{\Delta }{\mathrm{G}}_{\mathit{bind}}^{°}$ is likely related to conformational sampling problems with the decoupled ligand in which strong, unscreened intramolecular electrostatic forces lead to kinetically trapped states. Note that the decoupled states of the gas-phase ligand appear in both $Z_{R_{\mathit{wat}}\dots L_{\mathit{gas}}}$ and $Z_{L_{\mathit{gas}}}$ in Eq. (9.2) and Eq. (9.4) (Supporting Information); in the limit of infinite sampling time, the two setups should yield the identical result. However, in practice, where the simulation time is finite, we found that the DDM setup with the nonbonded intramolecular interactions turned off in the decoupled ligand yielded more accurate results. By comparing the conformations of the fully decoupled ligands sampled by the decoupling simulations, we found that retaining the intramolecular interactions in the decoupled ligand resulted in sampling problems as the ligand can be kinetically trapped in more compact conformations because of the unscreened intramolecular electrostatic interactions. One representative structure of such kinetically trapped conformations sampled during the decoupling simulations is shown Fig. 7A. While such compact conformations are over-represented in the simulations that decouple the ligand from the bulk solvent, they are underrepresented in the simulations that decouple the ligand from the DNA binding site. This reflects conformational sampling problems caused by strong ligand intramolecular interactions. In the DDM setup with the intramolecular nonbonded interactions turned off, such conformational sampling problems with the decoupled ligand states are avoided (Fig. 7B). As a result, for the quindoline derivative which carries a flexible and highly polar side chain, turning off the intramolecular interactions in the decoupled ligand leads to better $\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}^{°}$ estimates from DDM.

Figure 7.

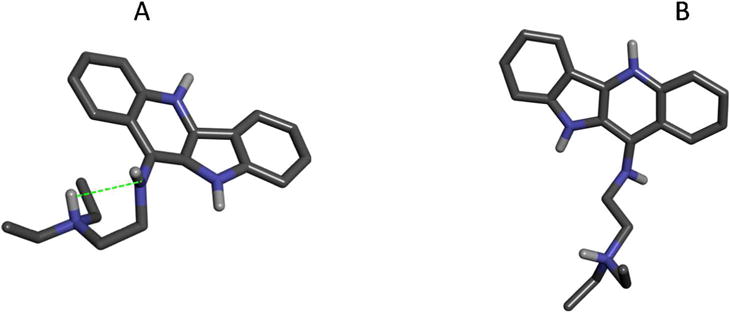
(A) A representative structure of a fully decoupled ligand sampled without switching off the ligand intramolecular interaction. The green dotted line indicates an electrostatic intramolecular interaction in the quindoline side chain. (B) A structure of the fully decoupled ligand sampled with the intramolecular nonbonded interactions turned off.

Energetically unfavorable water molecules may contribute to the instability of the binding pockets in the apo G-quadruplex

To help understand the reason why the binding pockets are unstable in the free G-quadruplex, we analyzed the energetics of the water molecules that would occupy the unliganded binding cavities. Using the HSA method^58,72, we have identified thermodynamically favorable and unfavorable water molecules located inside the both binding pockets based on an energetic cutoff of −9.53 kcal/mol, the energy of a TIP3P⁶⁵ bulk water molecule (see Methods, Fig. 8). The 5′ cavity contains two energetically unfavorable hydration sites in the back of the cavity while the 3′ cavity contains three energetically unfavorable hydration sites in the shallow groove of this binding cavity (Table S1 and S2, Supporting Information). In these cases, the energetically unfavorable water molecules which are located in partially enclosed regions of the binding site are unable to simultaneously maintain favorable energetic contacts with both the solute surface and neighboring water molecules. In addition, many energetically favorable water molecules in both cavities are only slightly more favorable than bulk water and make poor interactions with the solute surface as reflected in small number of solute-water hydrogen bonds and overall high solute-water energies (Tables S1 and S2). The energetics of the cavity water molecules, therefore, provide a physical explanation for the role of water displacement in binding and the reorganization upon unbinding because the weak solute-water interactions can be readily compensated either by the strong direct ligand-cavity interactions or the favorable intramolecular collapse of the binding pockets in the absence of the ligand, which is observed in both the NMR study and our computation simulations.

Figure 8.

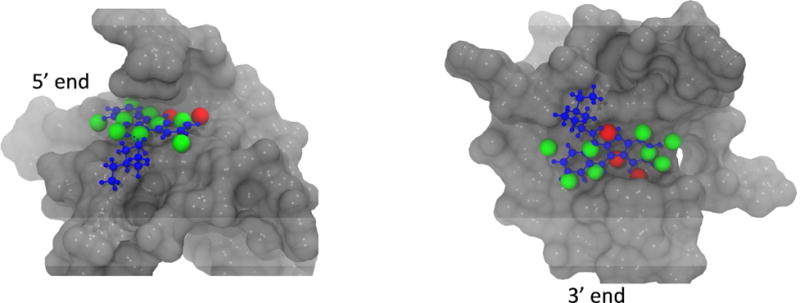
Hydration sites overlapping with the ligand (blue) in the 5′ end and 3′ end binding cavities. Hydrations sites with energies greater than −9.53 kcal/mol are shown in red and hydration sites with energies less than −9.53 kcal/mol are shown in green. See also Table S1 and S2.

DISCUSSIONS

Most of the previous computational studies of small molecule binding with nucleic acids have used the end-point method MM-PB(GB)/SA (molecular mechanics-Poisson-Boltzmann/generalized Born/surface area)^31,76–78. While these studies have provided insights into the energetics of ligand-DNA binding, the MM-PB(GB)/SA method has limited accuracy due to its intrinsic approximation of energy contributions from receptor conformational change and solvent effect^79,80. In this study we show that using statistical mechanics-based methods DDM and PMF, the absolute binding free energy of a potent ligand of the c-MYC G-quadruplex DNA can be computed reasonably accurately to within ~ 2 kcal/mol from the experiment (Table 2). The accuracy in the calculated absolute binding free energy obtained here is similar to that reported recently by Moraca et al. who applied metadynamics to study the binding of alkaloid berberine to a human telomeric G-quadruplex⁸¹. The results from that study and from the present work demonstrate the potential utility of statistical mechanics based absolute binding free energy methods in characterizing the thermodynamics of ligand-DNA binding. Comparing with MM-PB(GB)/SA, the improvement from these molecular dynamics based methods can be attributed to two key factors: first, the effects of binding pocket reorganization induced by the ligand binding/unbinding, such as those shown in Fig. 5, can be captured by MD-based free energy methods; second, the effect of structured water molecules on binding can be accounted for naturally by these explicit solvent based methods. We are testing whether the promising results reported here can be extended broadly to more diverse ligand-DNA complexes.

According to both PMF and DDM calculations, the 5′ site binds the quindoline with slightly higher affinities compared with the 3′ site (Table 2). We compare this computational result with NMR experiments on the 2:1 quindoline-G-quadruplex²⁹. In pH 7 and 100 mM K⁺ solution, the NMR spectrum for the 3′-flanking segment T23, A24 and A25 are not well resolved compared with the 5′ binding site, indicating that the 3′-end are more flexible and may exist in multiple conformations. This suggests that under the physiological conditions the quindoline-G-quadruplex complex at the 5′-end is more stable than the 3′-end complex, which is consistent with the computational result that quindoline shows a slight preference for binding at the 5′-end. Furthermore, the DDM calculations provide a plausible explanation for this binding site specificity. As seen from Table 4 and Table 5, the electrostatic free energy contribution actually favors the binding at the 3′-end, which likely reflects the intermolecular hydrogen bond formed at the 3′ site. However, this is outweighed by the nonpolar free energy contribution which much more significantly favors the binding at the 5′ site, which is related to a greater hydrophobic enclosure at the 5′ end. Consequently, the 5′ complex is slightly more stable than the 3′ complex. A very recent report on another quindoline derivative 4bm with an aromatic ring-containing side-chain showed an even stronger binding preference at the 5′ end of the c-MYC G-quadruplex⁸². This result could be nicely explained by our computational study: first, the aromatic ring-containing side chain of the 4bm is likely to favor the nonpolar interactions at the 5′-end even more than the quindoline molecule studied in this work does: compare Fig. 9 with Fig. 1A; second, because the 4bm features a CH₃ group attached to the positively charged nitrogen atom in the quindoline ring, it is unable to form intermolecular hydrogen bond with the O4 atom of the T23 at the 3′-end, which would further reduce the binding at the 3′ end.

Figure 9.

The 2D structure of the quindoline derivative 4bm studied in the Reference⁸¹.

In this work the PMF calculations suggest that the unbinding of the ligand causes major conformational changes in the flanking residues at both the 5′- and 3′-ends, resulting in the collapse of the binding cavities in the free c-MYC G-quadruplex (Fig. 5). This observation from the simulation supports the notion that the binding pockets in the G-quadruplex are not preformed but induced by the ligand, a result consistent with the solution NMR structures of the apo and holo G-quadruplex²⁹. The observation of the ligand-induced conformational rearrangements of the flanking residues forming the binding pockets is also supported by the binding kinetics measurements: the on rate of association k_on observed in SPR is several orders of magnitude slower than the diffusion-limiting values (Table 1). This could be caused by the kinetic barrier encountered by the incoming ligand to induce the formation of the binding pocket.

The quindoline-induced conformational rearrangement in the flanking segments observed in both the computer simulations and previous NMR structures provide important considerations for the biologically important parallel G-quadruplexes in gene promoters. As shown in the complex structures by NMR²⁹ and by computational simulations here, for the induced drug binding pocket to form, an appropriate single-stranded flanking segment containing at least two bases must exist. There is clear evidence of extensive single-stranded regions at either side of the G-quadruplex in a duplex element under negative supercoiled conditions⁸³. The inherent conformational flexibility of the DNA backbone in the single-stranded region flanking the G-quadruplex in gene promoters would likely provide an environment for the observed drug binding pockets to form.

Intriguingly, the calculated binding affinity of 0.39 μM (converted from the PMF-calculated binding free energy of −8.8 kcal/mol, see Table 2) is in close agreement with the IC₅₀ of 0.3 μM of the inhibition of the expression of c-MYC in the cancer cell line by the same ligand²⁶. While IC₅₀ is not a direct indicator of binding affinity, the two are closely related⁸⁴. Since the conformational reorganization of the flanking segments is crucial to the binding pocket formation, the fact that our calculated binding affinity correlates well with the experimental IC₅₀ of inhibition in the cell line assay provides an additional validation for the computational results, and it supports the view that the observed conformational dynamics likely plays a similar role in the flanking regions around the G-quadruplex formed in the c-MYC promoter. Further evidence that the binding pockets formed by the flanking segments of the c-MYC G-quadruplex are relevant drug targets comes from recent studies^31,33 of in silico virtual screening targeting the NMR structures of the c-MYC G-quadruplex^24,29. In these studies candidate ligands are docked into the binding sites formed by the flanking residues of the c-MYC G-quadruplex molecule from the NMR structures of the drug complexes. These modeling work have either led to the discovery of G-quadruplex-selective binders with micromolar activities³¹, or helped rationalize the binding mechanism of new active compounds³³.

The results of this work have implications for structure-based rational design targeting the c-MYC G-quadruplex. First, our results show that it is possible to obtain accurate absolute binding free energies for binding of charged ligand with DNA using the statistical mechanics-based methods DDM and PMF. These more detailed methods, although slower than docking and MM-PB(GB)/SA, can provide greater accuracy and could be employed in the post-docking refinement stage to more reliably identify true binders to help prioritize synthetic chemistry in drug design. Second, the results suggest that absolute binding free energy calculations can shed lights on binding site selectivity, which is difficult to obtain by experimental methods such as ITC and SPR. Such calculations can be useful for discovering ligands that selectively bind G-quadruplex relative to duplex DNA³¹. Third, the finding that the 5′ end flanking segment of the c-Myc G-quadruplex can rearrange itself to form more hydrophobically enclosed binding pocket suggests that the 5′ site could be the primary focus of in silico virtual screening of small molecule libraries. Furthermore, the observation that ligand binding induces conformational rearrangement in the flanking residues of the G-quadruplex suggests that an in silico virtual screening should optimally target the holo structures of the G-quadruplex generated from either NMR or MD simulation, instead of targeting the apo structure of the c-MYC G-quadruplex^30,31.

CONCLUSIONS

We report absolute binding free energy calculations on the quindoline-c-MYC G-quadruplex complex using two statistical mechanics-based free energy simulation methods DDM and PMF. The study shows that small molecule binding affinities at two different binding sites within one DNA G-quadruplex structure can be computed in good agreement with the experiment. While equilibrium binding constants can be determined by experimental methods such as ITC and SPR, these methods can not directly measure the binding affinities at different binding sites. Our study also provides a plausible explanation for the binding site selectivity and the ligand-induced conformational reorganization in the c-MYC G-quadruplex. These insights could be important for structure-based rational design targeting the c-MYC G-quadruplex. The methods described in this study can be applied to other DNA or RNA systems to aid in the interpretation of experiments and inform rational drug discovery targeting nucleic acids.