PaSD-qc: quality control for single cell whole-genome sequencing data using power spectral density estimation

Abstract

Single cell whole-genome sequencing (scWGS) is providing novel insights into the nature of genetic heterogeneity in normal and diseased cells. However, the whole-genome amplification process required for scWGS introduces biases into the resulting sequencing that can confound downstream analysis. Here, we present a statistical method, with an accompanying package PaSD-qc (Power Spectral Density-qc), that evaluates the properties and quality of single cell libraries. It uses a modified power spectral density to assess amplification uniformity, amplicon size distribution, autocovariance and inter-sample consistency as well as to identify chromosomes with aberrant read-density profiles due either to copy alterations or poor amplification. These metrics provide a standard way to compare the quality of single cell samples as well as yield information necessary to improve variant calling strategies. We demonstrate the usefulness of this tool in comparing the properties of scWGS protocols, identifying potential chromosomal copy number variation, determining chromosomal and subchromosomal regions of poor amplification, and selecting high-quality libraries from low-coverage data for deep sequencing. The software is available free and open-source at https://github.com/parklab/PaSDqc.

INTRODUCTION

Whole-genome DNA sequencing of single cells (scWGS) has recently been made possible by the introduction of single cell amplification methods. Multiple displacement amplification (MDA) employs a highly processive polymerase which can synthesize new molecules (amplicons) of ∼10–100 kb. High-quality MDA-derived data show that >90% of the human genome is amplified and 40–60% can be covered at >30× when the average depth is ∼40–50× (1). Copy number variations identified from low-coverage (<5×) MDA data have been used to elucidate tumor evolution (2) and to profile mosaic copy number variation (3). With the decrease in cost of deep whole-genome sequencing, more recently, high-coverage (>30×) MDA data have allowed detection of transposable element insertions and somatic single nucleotide variants in the human brain (1,4). Another protocol is multiple annealing and looping-based amplification cycles (MALBAC), which amplifies the genome in ∼0.3–5 kb fragments and can cover ∼50–90% of the human genome (5). It has recently been proposed as a method for screening in-vitro fertilized embryos for genetic abnormalities prior to implantation (6,7). A third method based on DOP-PCR can amplify ∼10% of the genome and is suitable for copy number variation detection but not single nucleotide variant detection (8).

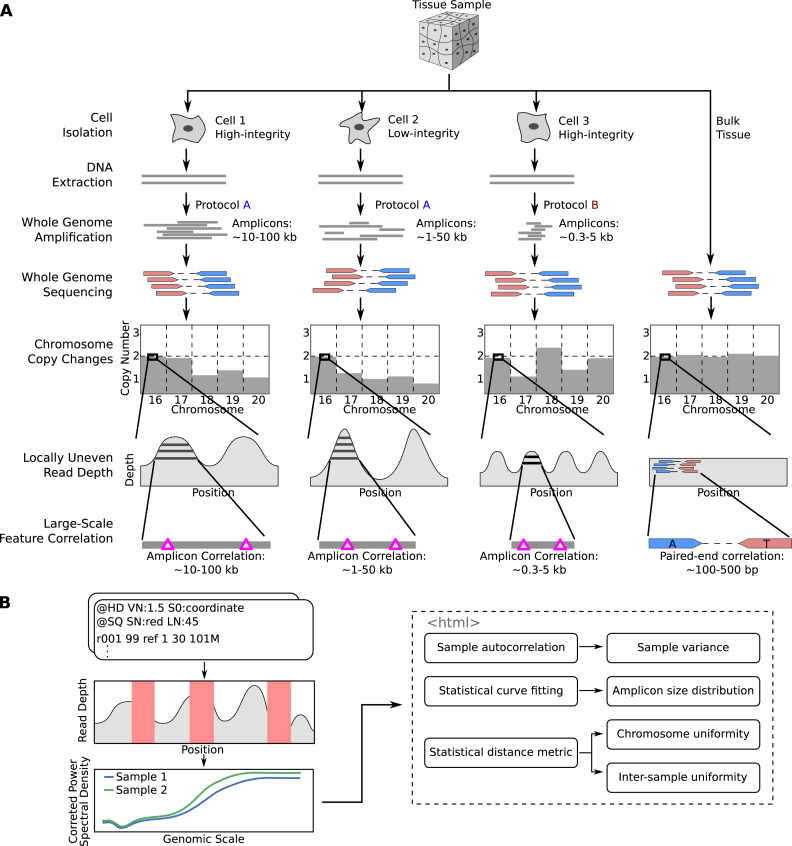
All scWGS amplification methods induce biases and artefacts. These include non-uniform read depth that can appear as copy number aberrations, under and over amplification of entire chromosomes, uneven amplification of the two alleles, and correlation of features at the amplicon scale (e.g. ∼10–100 kb for MDA) (9,10), as well as single nucleotide and indel mutations and random ligation of fragments that are hard to distinguish from inversions. These biases fluctuate depending on the exact amplification protocol used and the state of the isolated cell (Figure 1A). For example, heat lysis during DNA extraction can increase the rate of artefactual C>T mutations compared to alkaline lysis (11), and cells in the G2/M phase amplify more uniformly than cells in the G1/G0 phase (12). These biases in the data can affect the accuracy of variants detected in downstream analysis, and new protocols are frequently proposed claiming to mitigate these biases and provide superior variant detection (13–15). It is thus important to characterize the biases computationally and assess the quality of single cell data.

Figure 1.

Overview of single cell whole-genome sequencing and sources of artefacts, and the PaSD-qc pipeline. (A) Schematic overview of single-cell whole genome sequencing and the artefacts created by whole-genome amplification. The extent and patterns of the biases depend on the cell condition (high- or low-integrity) and on the scWGS protocol used (protocol A or protocol B). The pink triangles in the ‘Large-Scale Feature Correlation’ represent genomic events (e.g., single nucleotide variants) which are spanned by a single amplicon and are thus correlated. The only correlation pattern present in bulk sequencing is due to paired-end sequencing, represented by positions marked ‘A’ and ‘T’ spanned by the mate pair. (B) Schematic overview of the PaSD-qc pipeline. Read depth is extracted from bam files at uniquely mappable positions. Red rectangles represent regions where the true read depth is unknown due to low mappability, locus dropout, or sequencing bias. PaSD-qc uses a custom power spectral density estimation procedure to accurately estimate the correlation patterns in the data, and these patterns are then used to assess amplification properties and quality control measures. By default, the results are summarized in an interactive HTML report.

Despite the growing popularity of scWGS, few methods exist to perform this evaluation, and the few that do are almost exclusively concerned with estimating the uniformity of amplification. This itself is a non-trivial task because the true amplification process is masked by non-unique mappability, locus dropout due to amplification failure, or sampling bias during sequencing; additionally, read depth is highly correlated at positions spanned by the same amplicon. Current methods fail to account for these challenges. For example, several methods estimate read depth variance by binning reads (15,16). Such methods evaluate dispersion at a fixed genomic scale (the bin size), which fails to capture the correlation patterns of scWGS; resolving this requires re-binning at many scales, which is time-intensive and computationally expensive. More recently, an autocovariance (ACF) method has been proposed (10). In theory, ACF is an appealing choice to capture the patterns in scWGS data because it measures correlations between observations within a dataset; however, in practice algorithms to estimate the ACF cannot easily be modified to account for regions of low mappability or locus dropout. Additionally, no standard implementations of these tools are available for incorporation into an scWGS pipeline.

Here, we introduce a suite of tools to comprehensively measure scWGS data quality, in a package called PaSD-qc (Power Spectral Density-qc, pronounced ‘passed-qc’). Using techniques from digital signal processing to estimate the power spectral density (PSD) of a sample and correct for observation gaps due to non-unique mappability, assembly gaps, and locus dropout without the need for binning, PaSD-qc provides a robust assessment of amplification uniformity at all genomic scales simultaneously. Because our method accounts for the uneven spacing of the data while concurrently reducing background noise, the PSD can be leveraged to obtain more accurate estimates of variance and autocovariance than other methods; to quickly identify chromosomes which may be copy-altered; to discover chromosomes and sub-chromosomal regions of poor amplification; and to compare quality across jointly analysed samples even at very low coverage (<0.1×). Furthermore, our statistical method can estimate the full distribution of amplicon sizes in a sample, which has not previously been possible. PaSD-qc can easily be incorporated into existing pipelines and by default summarizes the quality and properties of each sample in an interactive HTML report. We use the tool to profile several different scWGS protocols, compare different samples from the same protocol, and select high-quality libraries from an initial set of low coverage (<1×) data for full-depth sequencing.

MATERIALS AND METHODS

Data

MDA data from neurons of phenotypically normal individuals ‘4638’ (Brain A), ‘1465’ (Brain B), and ‘4643’ (Brain C) were previously obtained by our group (4). Additionally, three muscles cells from the 1465 individual were isolated, amplified, and sequenced as in that study. Thirty-three additional MDA samples from human cells obtained for studying chromothripsis (C1a/b, C2a/b, C3a, N1a/b, N2a/b, N3a, N4a/b, MN1–6a/b, MN8a/b, MN9a-e) were obtained from (17). The MN cells were treated in such a way as to induce cell-specific copy losses and copy gains of entire chromosomes. MALBAC samples were obtained from (5), and the DOP-PCR sample from (2). In Figure 2, the bulk sample is bulk cortex from 1465, the MDA sample is cell 30 from 1465. All data were aligned to GRCh37 with decoy using GATK best practices. Downsampling of samples to uniform coverage (0.1×, 1× or 5×) was performed using SAMtools.

Figure 2.

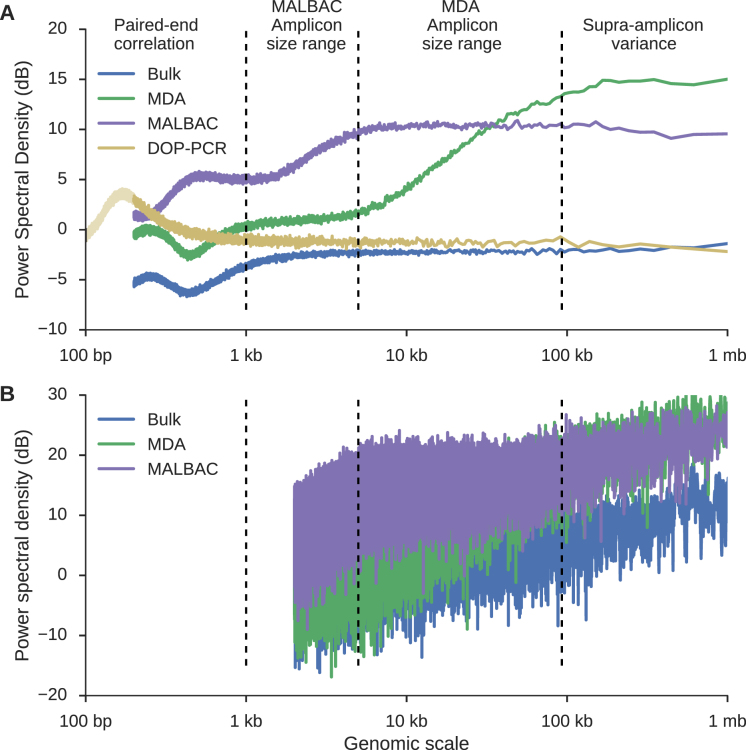
Using power spectral density to infer sample-specific amplification properties of scWGS data. (A) PaSD-qc power spectral densities for a bulk sample (blue), MDA sample (green), MALBAC sample (purple), and DOP-PCR sample (gold). The very low noise of the estimates allows amplification properties of the three samples to be inferred, including the paired-end insert size distributions (Supplementary Figure S1), the range of amplicon sizes for MDA (∼5–100 kb) and MALBAC (∼1–5 kb), and the sub- and supra-amplicon variances of the two amplification protocols. Interestingly, whereas MDA has a higher supra-amplicon variance than MALBAC, its sub-amplicon variance is considerably lower. DOP-PCR has the lowest supra-amplicon variance but the highest variance at small-genomic scales; as shown by the faded portion of the DOP-PCR curve, its variance peaks at 200–300 bp consistent with sonication of DNA to this size prior to amplification. (B) Power spectral density estimates using the algorithm from Leung et al. (13). A similar algorithm is used in Zong et al. (5). Background noise dominates the estimates making feature extraction infeasible. Resolution was limited to 2 kb because the data were binned into 1 kb bins as suggested per those algorithms. The DOP-PCR curve is not shown for clarity.

Power spectral density estimation

Starting with a BAM file, read depth for each arm of each chromosome is extracted as the time series 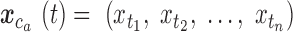where is the chromosome, 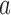is the chromosome arm and 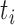is the start position of a uniquely mappable read. Uniquely mappable positions for the hg19 genome were download from the UCSC genome browser. By default, PaSD-qc uses mappability tracks calculated for 100 bp reads. Any series with fewer than 10 million observations is removed from further analysis. Each series 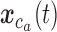is then divided into 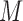windows of length 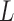overlapping by 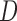positions. By default, 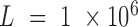and 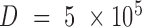. The Lomb-Scargle algorithm (18,19) is used to calculate the power spectral density, 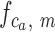, for each 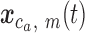at eight thousand frequencies, 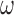, evenly spaced from 1e–6 to 5e–3 where frequency has units 1 / genomic length (bp). The PSD for each chromosome is then estimated using a modified Welch method (20) as

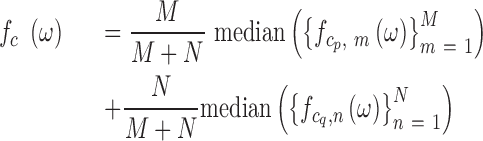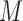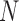where and are the number of windows on the 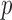and 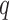arms of chromosome 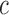, respectively. The average PSD for an individual sample is then calculated as 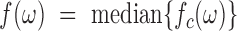. The standard error of the sample average PSD for each 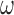is estimated using the usual sum of squared deviation from the mean formula. The mathematical details of Lomb-Scargle PSD estimation are described in supplemental information (SI). The theoretical justification for the power spectral density as a measure of variance in an aperiodic signal is also given in SI.

Normalizing and plotting power spectral densities

To remove edge effects and effects arising purely from sequencing, we take an idealized bulk sample as the baseline for the read depth power spectral density. The idealized bulk PSD, 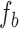, was derived by fitting a lowess curve to the PSD of the 1465 bulk cortex sample. The spectral density for each single cell sample is then normalized using the decibel transform as

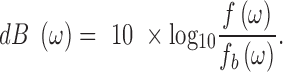This transform is standard in digital signal processing to remove a background signal.

Traditionally, power spectral densities are plotted as a function of frequency. However, for the genomic read depth signal, frequency takes on the unintuitive units of inverse genomic scale (1/bp). We instead choose to plot the PSD as a function of period, 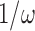. This results in the familiar units of genomic scale (bp) on the x-axis. We believe this eases interpretation, especially for those unfamiliar with power spectral densities. The value of the y-axis (dB) can be interpreted as a measure of variance relative to bulk sequencing, with higher values reflecting higher variance in the read depth signal.

Estimating the distribution of amplicon sizes from the power spectral density

As motivated in ‘Results’, the dynamic portion of the scWGS PSD curve reflects the cumulative distribution of the amplicon sizes in that sample. This distribution can thus be estimated by fitting a linearly scaled cumulative distribution function to this dynamic region. In practice, which distribution function should be fit is governed by two principles: (i) how tractable is fitting the curve using modern gradient descent algorithms and (ii) how well does the estimated distribution reproduce the original data. The first problem is one purely of computation and amounts to whether the distribution function has a closed-form solution or easily approximated integral solution. We tested three distributions which fit this criterion: the normal (erf), logistic, and gamma distributions. To solve the second problem, we used the estimated density to simulate an idealized amplification process and compared the PSD of the idealized process to that of the original sample. The simulation procedure is described in the section below. We found the normal (erf) distribution best reproduced the data.

Let 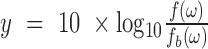and 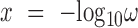. The dynamic region of the curve is fit as

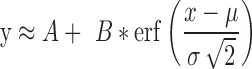where 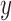can be viewed as an erf-smoothed PSD. The log10-transformed density of the amplicon sizes is then given by 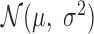, so the amplicon size distribution is log-normal with mean parameter 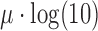and scale parameter 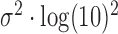(see SI). The mean, median, and variance of the amplicon distribution are estimated analytically from the log-normal distribution. However, there is no analytical form for confidence intervals of the log-normal distribution, so to estimate the 95% bounds, we draw 100 000 observations from the above normal distribution and calculate the percentiles of 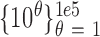, where 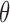is a simulated observation.

Simulating an idealized amplification process

Let 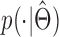be the log-distribution of amplicon sizes estimated using the above method. For a given chromosome arm, an idealized amplification process is simulated using the following algorithm:

1. Initialize a vector, 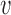, of length equal to the length of the chromosome arm with all entries zero.

2. Randomly simulate an amplicon size as 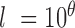where .

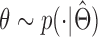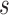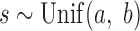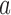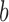3. Randomly choose a starting position , where where and are the start and end coordinates of the chromosome arm

4. Increase the values of the entries of 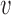overlapped by the amplicon by one

   1. Note: if 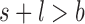, the simulated amplicon is discarded
5. Repeat 2–5 until the desired average depth of coverage is reached.

   1. Depth of coverage is calculated as .

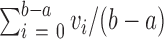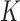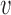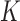6. Randomly choose non-zero observations from where is the number of non-zero observations from the chromosome arm in the original data.

The PSD of the resulting simulated read depth signal is then estimated and normalized as described above. To account for total power differences and mean shifts between the simulated data and the true data due to the idealized nature of the above algorithm, we normalize each curve by the maximum observed power and mean shift each curve such that 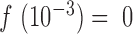. We chose to use the p arm of chromosome 3 for simulation purposes as in our experience it is a large arm with highly consistent amplification across samples. This simulation is idealized, as it treats the size and position of each amplicon as independent. Specifically for MALBAC, the location of amplified regions is non-random (1), so the simulation may not capture the full complexity of a true amplification process, leading to differences between the observed results and simulated results.

Estimating the autocovariance function

The autocovariance function, 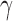, estimates the covariance of a time series against itself at lags 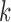. As derived in SI, the real-valued sample autocovariance can be estimated from the PSD as

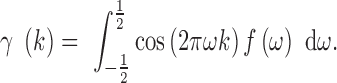This integral can be quickly and accurately estimated numerically using any modern quadrature technique. We use Simpson's rule.

To directly calculate the ACF from unevenly space time series data, we define the ‘observation’ function as

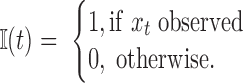For lag 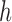we construct the set 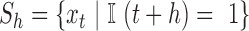, which is the set of all observations such that an observation at a distance of 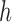is also present. The sample autocovariance is then calculated as

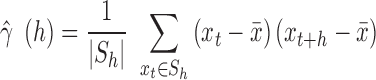where 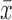is the sample mean of the time series and 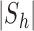denotes the size of 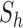. The estimate does not change perceptibly if the sample median is used for .

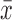Comparing the behaviour of different spectra

Given two probability densities, 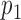and 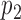and a vector of observations, 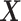, the Kullback-Leibler divergence is an informatic dissimilarity measure between the two densities and is defined as

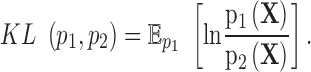It can be shown (see SI) that the Kullback-Leibler (KL) divergence between two PSDs is

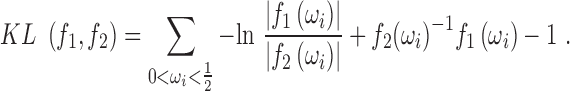The KL-divergence is not a true distance metric as 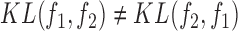. Following (21), we define the symmetric divergence between two spectra as

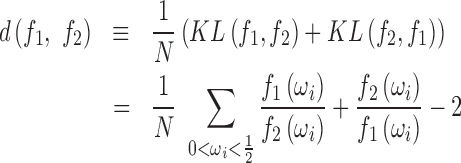where N is the total number of frequencies in the sum. This value is reflexive and always non-negative (see SI); thus 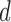is a principled statistical distance metric between two spectra.

To identify aberrantly amplified chromosomes, we calculate 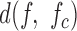for each chromosome of a sample. We then calculate the median divergence and the median absolute difference of the divergences. A chromosome is considered aberrant if its divergence is greater than the sum of the median and two times the median absolute difference. An aberrant chromosome is considered a possible copy loss if its entire erf-smoothed PSD lies three standard deviations below the sample average erf-smoothed PSD and is considered a copy gain if its erf-smoothed PSD lies three standard deviations above the sample average erf-smoothed PSD. In both cases we additionally require that the minimum vertical distance between the two curves occurs at the smallest evaluated genomic scale (1 kb). Otherwise an aberrant chromosome is considered poorly amplified.

To cluster samples by behaviour, the pairwise KL-divergence is calculated between each pair of sample PSDs. The resulting symmetric distance matrix is then used to perform hierarchical clustering.

Estimating median absolute pairwise difference

The BICseq2 algorithm (22) was used to calculate the copy number in bins of 1 kb, 5 kb, 10 kb, 50 kb, 100 kb, 500 kb and 1 mb for all 1465 and 4643 samples. Estimates were corrected for mappability and GC content. For each bin size, MAPD is calculated as 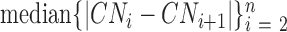, where 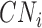is the copy number in the ith bin and 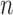is the total number of bins.

Estimating chromosome-level copy number

Both BIC-seq2 (22) and Ginkgo (23) were used to estimate copy number for each single cell sample using a bin size of 50 kb. Both algorithms gave similar results. Since Ginkgo provides whole-number copy number estimates, we chose to plot these results for ease of interpretation.

Implementation

PaSD-qc is implemented in python. It uses SAMtools to extract coverage from bam files and the astropy package (24) to implement an 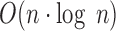Lomb-Scargle algorithm. The function curve_fit in the scipy module is used to fit the modified erf function to the scWGS PSD. Clustering of samples is performed by the linkage function also in the scipy module. PaSD-qc parallelizes across samples for efficient multi-sample analysis. Source code, documentation, and examples – including all data and code to reproduce the figures in this manuscript—are available at https://github.com/parklab/PaSDqc.

RESULTS

Characterizing the spatial correlation structure induced by whole-genome amplification

Figure 1B provides an overview of PaSD-qc, and precise details of the algorithm are described in Materials and Methods. In brief, to mitigate issues of mappability, locus dropout, and sequencing bias, we extract read depth only at uniquely mappable positions covered by at least one read. The resulting signal is a time series (indexed by genomic position) with highly unevenly spaced observations. To infer the correlation patterns within this series, we apply the Lomb-Scargle algorithm (18,19) to estimate the power spectral density (PSD) of the series. This method is one of the few which is capable of accurately analysing correlation patterns of unevenly spaced time series data. We additionally apply a Welch correction (20) to minimize the noise of power spectral density estimation.

PSDs measure the frequencies present in a time series, so if a signal oscillates every six units, the PSD will show a peak at the associated frequency of 1/6. This begs the question whether the PSD is an appropriate approach given that read depth is naturally an aperiodic signal (15). Rather, it can be shown (see SI) that the PSD exactly estimates the variance of an aperiodic signal, and further that it accurately captures all correlations present in the data, even when the observations are unevenly spaced. Thus, at any genomic scale, the PSD estimate from our method can be interpreted as the variance of the scWGS amplification at that genomic scale. Additionally, the shape of the curve reveals the correlation patterns induced by the amplification. For ease of interpretation we provide estimates relative to a bulk sample, resulting in the units of decibels (dB) for the PSD.

Illustrative examples of a bulk sample, an MDA sample, a MALBAC sample, and a DOP-PCR sample are shown in Figure 2A. Below a genomic scale of ∼1 kb, the bulk sample shows a characteristic pattern arising from paired-end sequencing. For a read pair with insert size 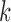starting at positon 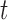, there will be an increase in signal at 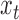and 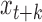and a decrease in signal between the two reads. This results in periodicity at small genomic scales with the strongest periodicity around the mode of the insert size distribution (350 bp for the bulk sample shown). In fact, at small genomic scales, the PSD resembles the distribution of insert sizes in a sample (Supplementary Figure S1). Above a genomic scale of ∼1 kb, the bulk sample is virtually flat with low amplitude, indicating that, as expected, the coverage profile from bulk sequencing has low-variance and has no large-scale correlation structure. The slight increase in the PSD at scales >100 kb is an edge effect of the Welch correction. This edge effect is removed from scWGS PSDs by using an idealized bulk sample as a baseline (see Materials and Methods).

The MDA and MALBAC curves have a more complex shape above the pair-end scale. To interpret these curves, consider an amplicon of length 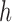starting at position 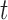. The read depth signal 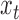will be correlated with 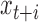for 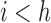. How often a correlation at length 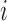is observed depends on the number of amplicons with length 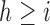. If 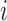is less than the smallest amplicon, then read depth 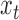and 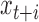will almost always be correlated, resulting in small local variance and thus a lower amplitude PSD at sub-amplicon scales. For length 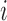greater than the largest amplicon, 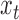and 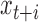are necessarily independent, resulting in a higher amplitude PSD at supra-amplicon scales, reflecting the unevenness of the amplification. The PSD will smoothly transition from the sub- to supra-amplicon variances precisely following the cumulative distribution of amplicon sizes. These patterns are apparent in Figure 2A. The MDA curve rises from ∼5–100 kb and the MALBAC curve rises from ∼1–5 kb, consistent with expected amplicon sizes for these protocols. Additionally, the supra-amplicon variance of the MALBAC library is lower than the supra-amplicon variance of the MDA library while the opposite is true of the sub-amplicon variances, reflecting that MALBAC provides more consistent amplification at positions far apart but that MDA is locally more uniform since two positions close together are likely to be spanned by a single amplicon. The DOP-PCR curve shows a peak in variance at 200–300 bp, consistent with the DNA being sonicated to this size prior to amplification; it then asymptotically approaches the variance of a bulk sample as expected. As DOP-PCR samples are sequenced to very low coverage (<<1×), the utility of our method is limited, so we do not further consider this amplification protocol.

We are not the first to propose power spectral density estimation as a uniformity measure. However, prior estimation procedures (5,13) require binning the data into 1 kb bins and do not take steps to reduce background noise. This results in an inferior PSD estimate where resolution is limited to a minimum genomic scale of 2 kb (since the Nyquist frequency is 5 × 10⁻⁴), and fine scale differences between samples are obscured by the high level of background noise (Figure 2B). Additionally, the PSD was criticized as lacking reproducibility since a Fourier transform may not be stable in regions of zero read depth or low mappability (15). As stated before, PaSD-qc corrects for these regions, resulting in highly reproducible estimates (Supplementary Figure S2).

Estimating the distribution of amplicon sizes in scWGS data

Since the dynamic region of the scWGS PSD curve reflects the cumulative distribution of amplicon sizes, this distribution can be estimated by fitting a properly scaled probability function to the PSD. The error function (erf) provides a particularly good fit (Figure 3A) and defines a density over the log₁₀ amplicon sizes of the form 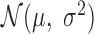(Figure 3B) where 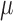and 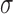are parameters estimated from the erf curve. 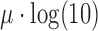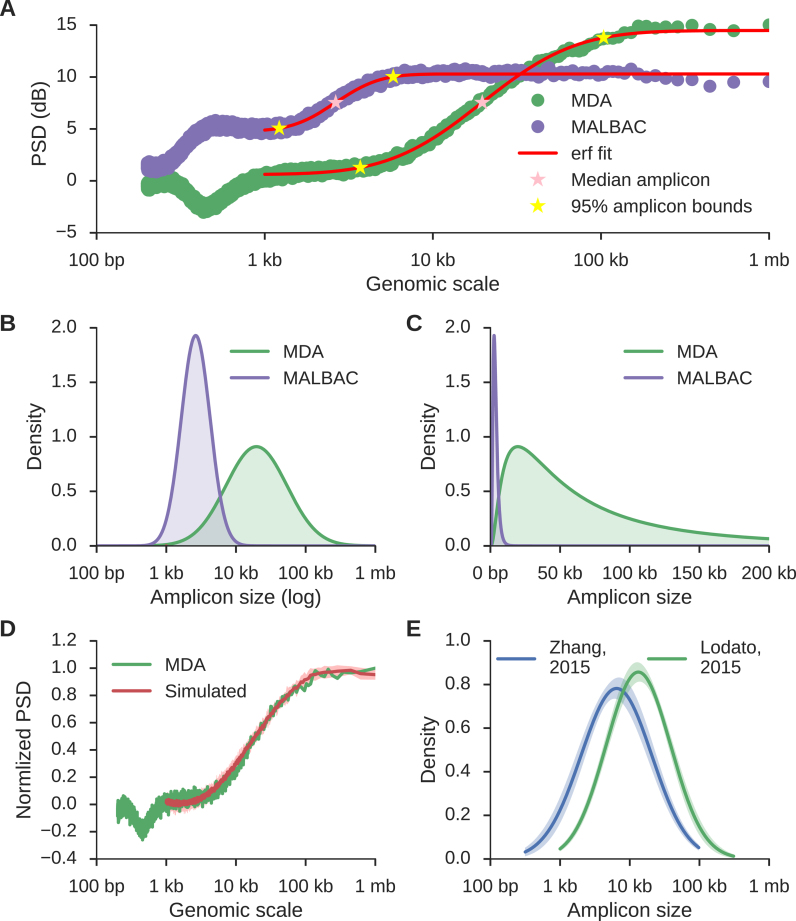In standard coordinates, the distributions are skewed with heavy tails extending into larger genomic ranges, following a log-normal distribution with mean and scale parameters and 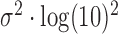, respectively (Figure 3C). To confirm the accuracy of this estimation, we simulated an idealized amplification process on the p-arm of chromosome 3 using the amplicon size distribution estimated from the MDA curve as the generative model (see Methods). The resulting read depth signal was then analysed using the PaSD-qc algorithm. Figure 3D shows the results of the simulation (red curve) along with the true estimate (green curve); Supplementary Figure S3 shows the simulated curve for the MALBAC sample. We additionally tested the logistic and gamma distributions as possible models (Supplementary Figure S3). While the logistic and erf functions produce similar fits, we opted to use the erf fit as it allows amplicon sizes to be modelled analytically using a log-normal distribution (see Materials and Methods). The simulated curves are over-dispersed for MALBAC, suggesting all three distributions overestimate the variance of MALBAC amplicons. However, we are limited to these density functions for two reasons: (i) the cumulative distribution must be sigmoidal and, more restrictively, (ii) the cumulative distribution must have a functional form which can be quickly and stably approximated using numerical methods. It is also possible that the idealized simulation process does not adequately capture the complex, small-scale dynamics of the MALBAC amplification process, leading to the observed over-dispersion (see Materials and Methods).

Figure 3.

The distribution of amplicon sizes can be directly estimated from the power spectral density. (A) MDA (green) and MALBAC (purple) curves as in Figure 2 along with the inferred error function (erf) fit of the dynamic region (red), the median amplicon size (pink stars), and 5% and 95% bounds on amplicon sizes (yellow stars). (B and C) Distributions of inferred amplicon sizes in the MDA and MALBAC sample. Densities are normally distributed in a log scale (B), but highly skewed according to a log-normal distribution in standard coordinates (C). (D) The average power spectral density (red) resulting from ten simulated amplification processes using the MDA density shown in (C) as the generative distribution. The shaded region represents the 95% confidence interval and the green curve corresponds to the original data. The MALBAC fit and fits using other distributions are shown in Supplementary Figure S3. (E) The average amplicon size distributions for 35 samples from Lodato et al. (4) (green) and 33 samples from Zhang et al. (17) (blue) reveal that different MDA protocols produce different amplicon size distributions, but a single protocol produces consistent amplicon size distributions across samples (shaded regions represent 95% confidence intervals around the average).

The median, mean and variance of the amplicon sizes per sample are determined analytically from the log-normal distribution while 5% and 95% confidence bounds are inferred using Monte Carlo simulation (see Materials and Methods). For the MDA sample, the median amplicon size is 19 kb and the 5% minimum and 95% maximum amplicon sizes are 3.7 and 103 kb, respectively; for the MALBAC sample, the median amplicon size is 2.6 kb and 5–95% bounds are 1.2 and 5.8 kb, respectively (Figure 3C). We additionally profiled the amplicon distribution of 35 samples from (4) and 33 samples from (17) at high coverage (∼5X) and found that distributions are consistent between samples amplified with the same protocol but divergent between different protocols (Figure 3E); samples using the Qiagen REPLI-g Single Cell Kit with heat lysis (17) have a smaller median amplicon size than samples using Epicenter RepliPHI Phi-29 with alkaline lysis (4) (13.3 ± 1.2 kb versus 6.4 ± 1.0 kb; P-value <1e–31 by Kolmogorov–Smirnov test).

A method for calculating the characteristic length scale of correlation in scWGS was previously proposed (10). We profiled four samples also profiled in that study and found our estimated median amplicon size was consistent with though slightly smaller than their characteristic length scale estimates (Supplementary Table S1). No other method estimates the full distribution of amplicon sizes in scWGS data. Our method is stable in the presence of chromosomal copy alterations and consistent at depths of 0.5× and greater, though there is a tendency to overestimate amplicon sizes at low coverages (Supplementary Figure S4).

Comparison to existing scWGS quality control metrics

The autocovariance function (ACF) of scWGS data has previously been proposed as a quality metric. While the ACF can be calculated directly from unevenly spaced time series data in theory, no computationally efficient algorithm exists to perform the estimation, and implementations are either time intensive, memory intensive, or both. Additionally, the statistical power at each lag varies and no theoretical results exist on the consistency of the unevenly spaced ACF estimator. However, it is possible and theoretically justified to calculate the ACF from the PSD (see SI). PaSD-qc implements an efficient algorithm based on this principle (see Materials and Methods).

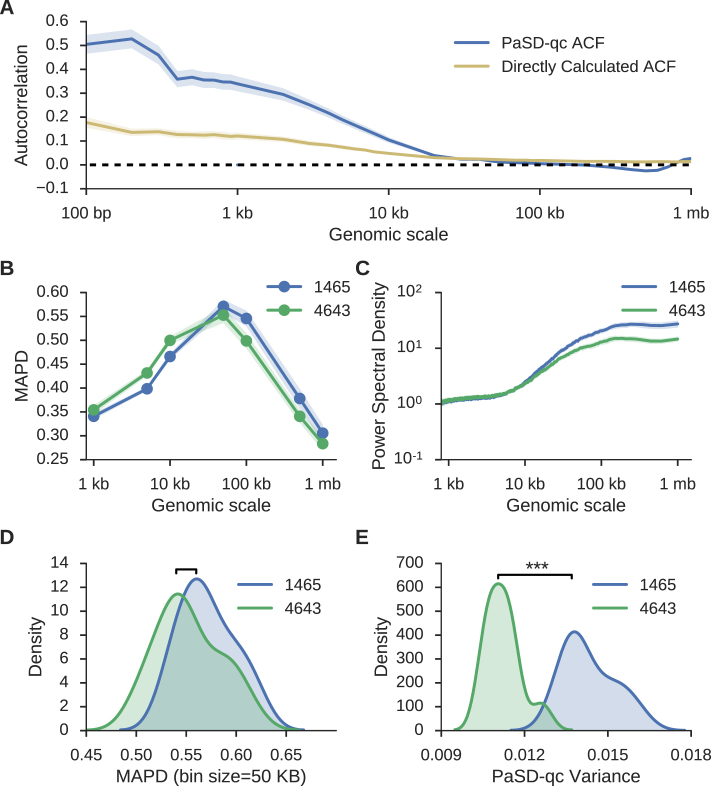
To compare the performance of the PaSD-qc ACF against the directly calculated estimate, we analysed all 16 single cell samples from the 1465 individual in (4) using both methods (Figure 4A). These samples were pair-end sequenced with an average insert size of 350 bp. The PaSD-qc ACF estimate consistently identifies the peak in correlation expected at this scale; the direct estimation fails to capture this feature. Additionally, the autocorrelation should oscillate around zero beyond the largest amplicon size. While this behaviour is present in the PaSD-qc ACF, the direct estimation remains positive beyond 1 mb, a genomic scale far larger than the upper amplicon size limit of the Phi-29 polymerase used in MDA. This empirically demonstrates the potential inaccuracy of directly calculating the ACF from highly unevenly spaced observations and illustrates how PaSD-qc surmounts this limitation.

Figure 4.

The PaSD-qc variance measure outperforms prior dispersion estimates. (A) Average sample autocovariance with 95% confidence intervals for the sixteen 1465 samples from Lodato et al. (4) as calculated by PaSD-qc (blue) and by direct estimation (gold). See text for a comparison. (B) Average MAPD scores with 95% confidence intervals calculated for seven bin sizes ranging from 1 kb to 1 mb for sixteen 1465 samples and eleven 4638 samples from Lodato et al. (C) The average power spectral density with 95% confidence intervals for the same samples. (D) Densities for the MAPD scores of the two sets of samples at 50 kb, the standard bin size at which the score is calculated. At this bin size, MAPD cannot distinguish behaviour of the two sets of samples. (E) Densities of PaSD-qc variance for the two sets of samples are significantly different.

Additionally, the ACF at lag zero (equivalently the integral of the PSD) provides an estimate of the overall variance. This dispersion estimate outperforms the other commonly used dispersion estimate, median absolute pairwise difference (MAPD) (16,25). MAPD is calculated by binning the read depth signal into fixed-width bins, calculating the copy number in each bin, and taking the median of the pair-wise differences between all neighbouring bins. We calculated MAPD scores at a range of bin sizes (Figure 4B) and the PaSD-qc PSD estimates (Figure 4C) for all 1465 and 4643 samples from (4). Both reveal 1465 samples have higher supra-amplicon variance than 4643 samples. However, calculating MAPD even at a single bin size is computationally intensive; as such, it is usually calculated only for a single bin size, often 50 kb. At this scale, MAPD fails to distinguish a difference between the sets of samples (Figure 4D, P-value: 0.11 by Kolmogorov–Smirnov test). However, the PaSD-qc variance readily discriminates the two sets (Figure 4E, P-value: 1.7e–6 by Kolmogorov–Smirnov test). Moreover, since MAPD requires estimating copy number, it becomes unreliable at small bin sizes because copy estimation in scWGS is inaccurate at genomic scales below ∼50 kb. This inaccuracy is appreciable in Figure 4B as MAPD in 4643 samples appears higher than in 1465 samples below 50 kb despite their having identical variances at these scales (Figure 4C).

Identification of chromosomes with potential copy number alterations and regions with amplification abnormalities

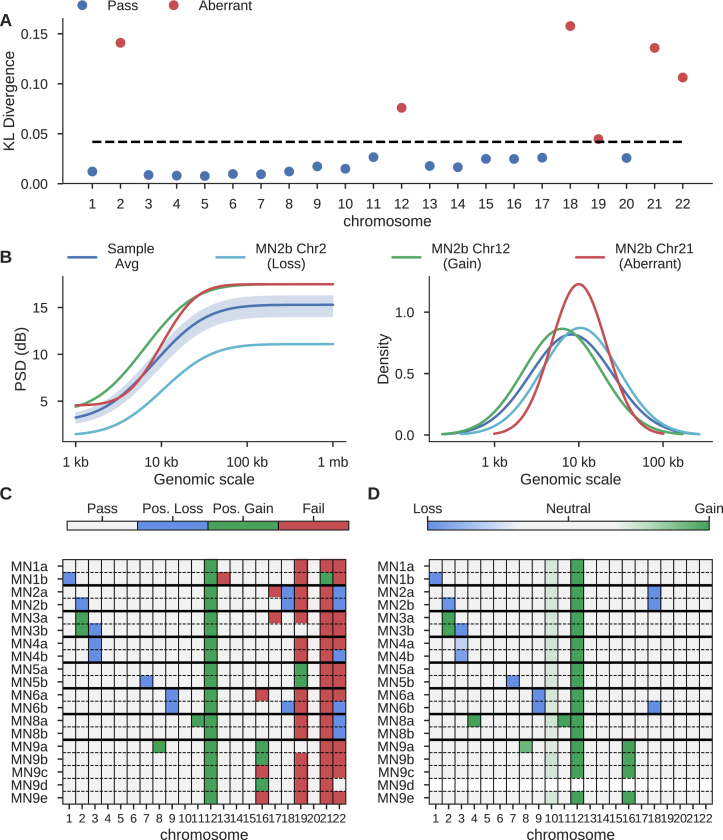
The close relationship between a power spectral density estimate and a normal distribution (21) permits the calculation of a statistical distance measure, the symmetric Kullback–Leibler (KL) divergence, between two spectra (see Materials and Methods). For a given sample, PaSD-qc identifies chromosomes with aberrant amplification patterns by calculating the distance of each chromosome's PSD from the sample-average PSD. A chromosome is considered aberrant if it's KL-divergence is two standard deviations beyond the sample median across all chromosomes (Figure 5A).

Figure 5.

Identification of copy-altered chromosomes and poorly amplified chromosomes. (A) KL-divergence between individual chromosomes and the sample average PSD of MN2b from (17). Black dashed line is two standard deviations above the median divergence. (B) The erf-smoothed PSD of the sample average (dark blue), a true copy-loss (light blue), a true copy-gain (green), and a suspected poorly amplified chromosome (red) (left panel), and the inferred amplicon distributions for the sample and the individual chromosomes (right panel). The shaded region is three standard deviations around the average sample PSD. (C) Classification of chromosomes at 1X coverage across all 19 micro-nucleated samples from (17) based on heuristic behaviour of each chromosome's PSD. (D) The average copy number of each chromosome as inferred using the Ginkgo algorithm.

To investigate how this classification behaves in the presence of true copy alterations, we analysed 19 samples from (17), which had rigorously validated cell-specific copy gains and losses. We found significant KL-divergence can be caused both by true chromosome copy changes and poor amplification. However, a chromosomal copy gain manifests as a large mean shift of the chromosomal PSD up from the sample average PSD whereas a deletion manifests as a mean shift down from the sample average. Chromosomes with altered amplification patterns generally have curves with shapes distinct from the sample average (Figure 5B, left panel; Supplementary Figure S5). This is further reflected in the chromosome-specific amplicon distributions; gains and losses have distributions similar to the sample average distribution, whereas aberrantly amplified chromosomes often have distinct distributions (Figure 5B, right panel; Supplementary Figure S5).

We developed a simple heuristic algorithm which uses these properties to categorize chromosomes as harbouring a possible copy loss, possible copy gain, or as aberrantly amplified (Figure 5C). This heuristic accurately identifies most true-positive whole-chromosome CNVs (37/40) as inferred by the BICseq2 and Ginkgo algorithms (Figure 5D) at the expense of a handful of false-positives (9/378). Chromosome 10 is not flagged in any sample as the gain effects only the q arm. Similarly, chromosome 4 of MN8a is not identified as the gain affects only part of the chromosome (Supplementary Figure S6). When only the q arms of these chromosomes are analysed, the gains are identifiable (Supplementary Figure S7). MN9d is masked in Figure 5D as the Ginkgo algorithm failed to provide meaningful calls (Supplementary Figure S6). At lower depths, the heuristic algorithm becomes more sensitive to copy gains, identifying 28/29 whole-chromosome copy gains at the expense of sensitivity to deletions, detecting 6/11. At high coverage, it becomes more specific for deletions (3/378 false-positives) at the expense of sensitivity to true-positive deletions (9/11) and gains (2/29) (Supplementary Figure S8). Chromosomes 19, 21 and 22 are identified as poorly amplified in most samples; they may be hard to amplify due to their high gene-density and GC content compared to other chromosomes, consistent with known difficulties of amplifying GC-rich sequences and further supported by the fact that other small chromosomes with lower gene-density and GC content (e.g. chromosomes 18 and 20) are not identified as aberrantly amplified.

This same method can be used to quickly identify sub-chromosomal regions which have aberrant amplification properties. In this use-case, a chromosome is treated as a sample, and each sub-region viewed as a pseudo-chromosome. PaSD-qc then identifies sub-regions with KL measures divergent from the chromosome average. This method identifies a large spike in coverage at the centromere of chromosome 1 in MN1a (Supplementary Figure S9). This analysis can be run in less than one minute for a given chromosome.

Discriminating high- and low-quality samples

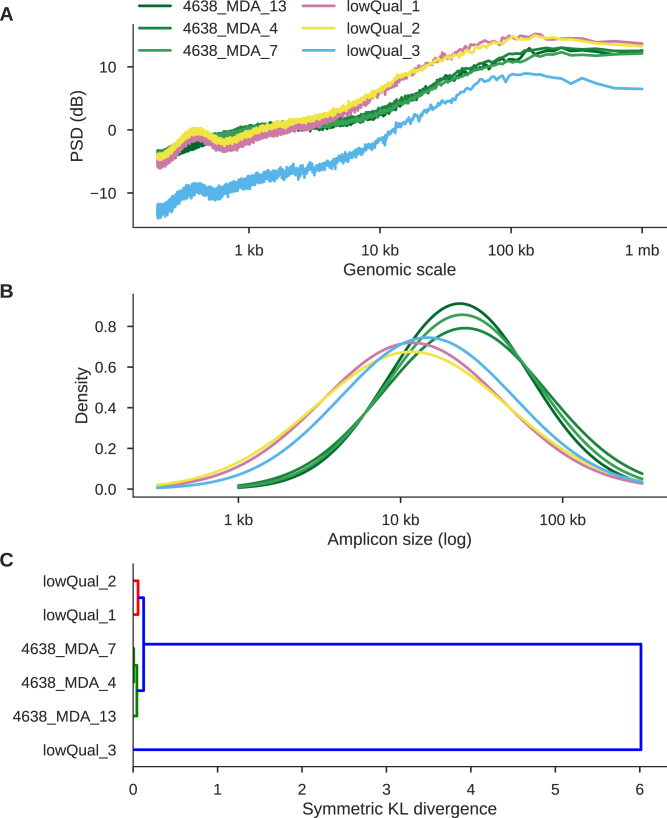
From previous sequencing data, we identified three samples of low quality (Supplementary Figure S10). Comparing them to high-quality samples from 4638 provides an illustrative example of how PaSD-qc can be used to distinguish high- and low-quality samples. Two samples (lowQual 1 and 2) have higher supra amplicon and total variance than 4638 samples whereas lowQual 3 behaves as if the entire sample were haploid (Figure 6A). This over-dispersion of read depth in lowQual 1 / 2 compared to 4638 samples and the ‘haploid-like’ behaviour of lowQual 3 are apparent by eye from the copy number profiles of these samples (Supplementary Figures S11). Additionally, all three lowQual samples have smaller median amplicon sizes and higher variance amplicon size distributions (Figure 6B).

Figure 6.

PaSD-qc separates high-quality from low-quality samples and groups similarly behaving libraries. (A) power spectral densities for three high-quality libraries (green) and three low quality libraries (pink, yellow, and blue). Genome-wide copy profiles support the higher dispersion of lowQual 2 and the haploid-like behaviour of lowQual 3 (Supplementary Figure S11). (B) Amplicon size density plots for the six samples. C. Hierarchical clustering using the symmetric KL-divergence.

PaSD-qc can cluster the libraries based on behaviour using the symmetric KL-divergence. Unsurprisingly, it clusters the 4638 samples, clusters lowQual 1 and 2, and places lowQual 3 on its own (Figure 6C). Finally, PaSD-qc can use the symmetric KL-divergence to probabilistically assign samples to different categories (e.g. high- and low-quality) using pre-computed gold-standard spectra. The toolbox is distributed with several pre-computed spectra from the data analysed in this paper and includes methods which allow users to generate gold-standard spectra from their own data. PaSD-qc can discriminate the quality of these six samples with coverage as low as 0.1X (Supplementary Figure S12). However, at this low coverage, the nuances of the PSD used to estimate the amplicon distribution and evaluate chromosome behaviour are diminished, precluding applying these methods.

DISCUSSION

Here, we have demonstrated the effectiveness of PaSD-qc to comprehensively evaluate the quality and amplification properties of scWGS data. Although several studies have recently compared the uniformity of different scWGS protocols (25–27), each study uses its own collection of statistics, making the task of determining the superior protocol difficult. We believe PaSD-qc represents an important step forward for the field as it provides a standardized suite of analyses that researchers can easily insert into any pipeline. In particular, PaSD-qc introduces novel methods to estimate the full distribution of amplicon sizes in a sample, identify individual chromosomes which may be copy-altered or poorly amplified, discover sub-chromosomal regions of aberrant amplification, and compare samples based on amplification behaviour.

These analyses not only allow comparisons across amplification protocols but also provide an important starting point for variant analysis. It was recently demonstrated that the correlation in allelic balance induced by the large amplicons of MDA can be exploited to increase the accuracy of single cell single nucleotide variant (SNV) calling (11). Dong et al. proposed a method employing a kernel smoothing algorithm that requires a user-defined bandwidth to compute the expected balance at a given genomic locus. The length of the bandwidth reflects the user's belief about the maximum distance at which informative correlation exists, and the authors suggest using a fixed bandwidth of 10 kb for all samples. However, PaSD-qc provides a principled, data-driven strategy to assign a tailored bandwidth to each individual sample as the 95% upper bound on amplicon sizes naturally defines a maximum correlation distance. PaSD-qc further allows users to determine the bandwidth for individual chromosomes or even sub-chromosomal regions, by applying amplicon distribution estimation to only that chromosome or region. Given that the accuracy of amplicon size estimation becomes more accurate as depth increases, we recommend running PaSD-qc at higher coverage (e.g. 5X) if results are being used to calibrate mutation detection algorithms.

Additionally, our results address the question of whether in vitro amplification of the human genome by the Phi-29 MDA polymerase (28) produces amplicons of 10–100 kb as documented in bacterial genomes (29). We found that some protocols approach the upper bound while others produce far smaller amplicons, with the lower bound in the 1–5 kb range. This has important consequences for PacBio or 10X Genomics sequencing on single cells in which fragments many kilobases in length are required. In particular, only some protocols may consistently produce large enough amplicons to make long-insert or haplotype-based sequencing possible. PaSD-qc provides a principled, efficient, and inexpensive way to measure a sample's suitability for these technologies using low coverage Illumina sequencing.

Our results demonstrate that it is possible to detect whole-chromosome copy alterations using power spectral density estimation. We present this method not to replace bone fide copy number callers but to guide further analysis. Copy calling algorithms can be time and computationally intensive. PaSD-qc can comprehensively profile many samples in a fraction of the time using far less computational resources. Pre-profiling with PaSD-qc would allow researchers to identify samples which may harbour whole-chromosome copy alterations and to prioritize further analysis of these samples. We developed a heuristic method for classifying chromosomes. Heuristics are generally not optimal, and we suspect a probabilistic classification algorithm trained on many validated CNVs will demonstrate superior performance. As the number of publicly available high-coverage samples increases, such an algorithm will become possible. Additionally, the heuristic was calibrated using MDA samples, and as such we do not recommend its use on samples amplified with other protocols.

In principle, it should be possible to apply this method to detect sub-chromosomal copy number alterations. However, there are virtually no validated sub-chromosomal copy events in high coverage scWGS to use as training data. We therefore currently recommend sub-chromosomal outlier detection only as a method of blacklisting regions which have altered amplification properties and thus may not yield accurate mutation detection.

Lastly, full mutational analysis at the single cell level requires high-coverage (>30×) sequencing, but the uneven quality of scWGS data, primarily due to the variable quality of cells, has often resulted in only a portion of the data generated being usable. The ability to accurately characterize data quality from low-coverage data suggests that a cost-effective approach in scWGS data generation is to screen a large number of cells at very low coverage (e.g. <0.1×) and select only a small number of high-quality candidates for additional sequencing. PaSD-qc provides an efficient computational framework to perform this evaluation. While the specific PaSD-qc metrics defining ‘high-quality’ samples will depend on the amplification protocol and particular application, in general lower sub-, supra- and overall variance is desirable; samples with less dispersed amplicon size distributions are usually of superior quality; and, most importantly, samples amplified using the same protocol should have highly similar PSDs. Samples with outlying PSDs should be discarded as poor quality.

AVAILABILITY

Source code, documentation, and examples – including all data and code to reproduce the figures in this manuscript – are available at https://github.com/parklab/PaSDqc.

BAM files for the 1465 individual from (4) are available for downloaded from the Short Read Archive (SRA) with accession number SRP042470; BAMs for 4638 and 4643 from (4) are available from SRA with accession numbers SRP061939. BAMs from (5) are available from SRA with accession number SRA060929 and from (17) with accession number SRP052954. The DOP-PCR sample was obtained from (2) and has SRA accession number SRX342583. The BAMs for the three additional lowQual samples shown in Figure 6 are available from the corresponding author upon reasonable request.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [1U01MH106883 to CAW, PJP]; National Institute of Neurological Disorders and Stroke [R01NS032457 to CAW, PJP]; National Institute on Aging [K99 AG054749 01 to MAL]; Harvard Ludwig Center [to PJP]. CAW is an investigator of the Howard Hughes Medical Institute. Funding for open access charge: NIH [1U01MH106883].

Conflict of interest statement. None declared.