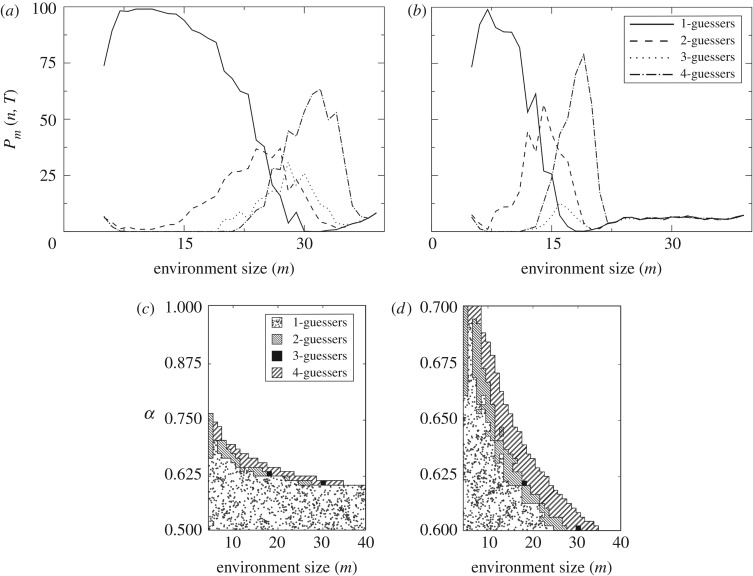
Figure 7.
Evolutionary drivers: competition. Coexisting replicators will affect each other’s environments in non-trivial ways which may often result in competition. We implement a dynamics in which 1-, 2-, 3- and 4-guessers exclusively occupy a finite number of environments of a given size (fixed m). The 100 available slots are randomly occupied at t=0 and granted to the best replicators as the dynamics proceed. We show Pm(n,t=10 000) for m=5,…,39 and α=0.6 (a) and α= 0.65 (b). The most abundant guesser at t=10 000 is shown for α∈(0.5,1) (c) and α∈(0.6,0.7) (d). Once m is fixed, there is an upper value of α above which no guesser survives and all 100 available slots remain empty. Competition and the replication-predictability trade-off segregate guessers according to the complexity of the environment—i.e. of the transmission channel. Coexistence of different guessers seems possible (e.g. m=15 in b), but it cannot be guaranteed that the dynamics have converged to a steady distribution.