Dynamics of convulsive seizure termination and postictal generalized EEG suppression

Bauer et al. show that seizures self-terminate through a mechanism that also determines the length of the postictal period. Using a computational model validated with EEG data, they show that the slowing of clonic movements at the end of seizures is related to the duration of postictal generalised EEG suppression.

Abstract

It is not fully understood how seizures terminate and why some seizures are followed by a period of complete brain activity suppression, postictal generalized EEG suppression. This is clinically relevant as there is a potential association between postictal generalized EEG suppression, cardiorespiratory arrest and sudden death following a seizure. We combined human encephalographic seizure data with data of a computational model of seizures to elucidate the neuronal network dynamics underlying seizure termination and the postictal generalized EEG suppression state. A multi-unit computational neural mass model of epileptic seizure termination and postictal recovery was developed. The model provided three predictions that were validated in EEG recordings of 48 convulsive seizures from 48 subjects with refractory focal epilepsy (20 females, age range 15–61 years). The duration of ictal and postictal generalized EEG suppression periods in human EEG followed a gamma probability distribution indicative of a deterministic process (shape parameter 2.6 and 1.5, respectively) as predicted by the model. In the model and in humans, the time between two clonic bursts increased exponentially from the start of the clonic phase of the seizure. The terminal interclonic interval, calculated using the projected terminal value of the log-linear fit of the clonic frequency decrease was correlated with the presence and duration of postictal suppression. The projected terminal interclonic interval explained 41% of the variation in postictal generalized EEG suppression duration (P < 0.02). Conversely, postictal generalized EEG suppression duration explained 34% of the variation in the last interclonic interval duration. Our findings suggest that postictal generalized EEG suppression is a separate brain state and that seizure termination is a plastic and autonomous process, reflected in increased duration of interclonic intervals that determine the duration of postictal generalized EEG suppression.

Introduction

Epilepsy is a paroxysmal neurological condition, characterized by sudden transitions from normal brain functioning to ictal states with synchronized neuronal oscillatory activity. Knowledge about seizure initiation or the transition from normal to ictal states is increasing, but less is known about seizure termination. Most convulsive seizures lead to a postictal state that is clinically and electrographically distinct from the ictal and interictal states. In the EEG this manifests as slowing, or as total suppression of the background activity, termed postictal generalized EEG suppression (PGES) (Lhatoo et al., 2010; So and Blume, 2010; Surges et al., 2011). During a PGES event, people are mostly immobile and in an unconscious state (Semmelroch et al., 2012; Seyal et al., 2013; Tao et al., 2013). This event is thought to be an extreme expression of the postictal state. As these events consistently preceded cardiorespiratory arrest in most reported ictal recordings of sudden unexpected death in epilepsy (SUDEP) they are likely to be of clinical relevance (Ryvlin et al., 2013). PGES frequently follows non-fatal convulsive seizures. Whether PGES is also a risk factor for SUDEP is a matter of debate (Lhatoo et al., 2010; Surges et al., 2011; Lamberts et al., 2013a).

Seizure termination may occur either due to a random process involving external perturbations or fluctuating state parameters, or to a deterministic, autonomous neuronal mechanism driven by the ictal condition itself (Lopes da Silva et al., 2003a, b; Kalitzin et al., 2010; Kramer et al., 2012; Stamoulis et al., 2013). Our objective was to clarify the type of dynamics underlying termination of convulsive seizures and the subsequent postictal state. We developed a computational neural mass model that autonomously transitioned between seizures and normal states. With the findings from this model we attempt to understand features of state transitions in EEG recordings of human convulsive seizures.

Computational models of seizures, based on neuronal lumps, have previously been used to describe global dynamics of state transitions. Seizure transitions are thought to occur in bistable systems where a stable ‘attractor state’ corresponds to normal activity and a second, transient quasi-stable ‘limit-cycle state’, represents seizures. Probability distribution statistics, particularly the gamma distribution, can be used to distinguish between stochastic, random walk type of processes and deterministic processes (Doob, 1953; Suffczynski et al., 2006). Seizure onset of some types of seizures was shown to have properties of a random walk-type stochastic process, while seizure termination may be influenced or even governed by deterministic processes (Koppert et al., 2011). This was consistent with experimental and clinical data (Suffczynski et al., 2006; Colic et al., 2013). In these studies, postictal states were not considered. We extend these findings to account for seizure termination and the postictal period. The computational model presented here is an extension of a model of multiple bi-stable units (Koppert et al., 2014), with added activity-driven connectivity dynamics. This model displays transitions from ictal to postictal and from postictal back to normal states. Critically, we tested and validated the hypotheses derived from this computational model against EEG recordings of convulsive seizures from 48 people with refractory epilepsy. A better understanding of the dynamics of seizure termination may help the development of new approaches to prevent the severe complications associated with PGES.

Materials and methods

The computational model

Computer simulations were carried out using a simplified lumped neuronal mass model created in Matlab® (release 2014b, The MathWorks Inc., Natick, MA, USA). The purpose of this abstract model is to explain the general dynamics of state changes in neuronal populations including pyramidal cells and interneurons while preserving essential properties of realistic neuronal networks (Kalitzin et al., 2014; Koppert et al., 2014).

The model consists of 128 fully interconnected units, with equal connectivity between any two units. Each single unit is a simple system that can have two dynamic states, depending on the chosen parameters. The first is a harmonic oscillator representing the normal, non-excited state of a neuronal mass. The second is a limit cycle attractor with permanent stable oscillations representing a micro-seizure (Izhikevich, 2001; Kalitzin et al., 2010). For certain parameter ranges both states co-exist (bistability), for other parameters values the unit is in one of the states. In the bi-stable regime the transitions between the two states can be induced by external inputs or by random fluctuations. In this study we use an analytical model that provides bistability in a relatively simple way. The model represents the collective dynamics of multiple pairs of excitatory and inhibitory populations, each represented by a complex variable $Z_m,\hspace{0.5em}m=\mathrm{1..}M$?>. These degrees of freedom incorporate the excitatory and inhibitory population dynamics as real and imaginary components correspondingly [$Z_m(t)=Ex{c}_m(t)+iIn{h}_m(t)$?>]. The original definition of the model (Koppert et al., 2014) is:

$$\frac{d}{dt}{Z}_m=-{\left|Z_m\right|}^4{Z}_m+b{\left|Z_m\right|}^2{Z}_m+c{Z}_m\hspace{0.5em}\hspace{0.5em}+i\omega Z_m+g(1+i){\displaystyle \sum }_{k=1}^N{C}_{mk}{Z}_k+{\sigma }_z\eta \left(t\right)$$ (1)

In the above equation, b, c and $\omega$?> are parameters of the single unit dynamics, the matrix $C_{mk}$?> represents the interactions between the units k and m, N is the total number of units in the network; g is a connectivity scaling coefficient, and $\eta \left(t\right)$?> is a random complex variable with normal distribution of unit variance; $\eta \left(t\right)$?> and the scaling coefficient ${\sigma }_z$?> introduce noise in the system. The factor (1 + i) reflects complex interactions between inhibitory and excitatory subunits in the system. The overall layout of the network and schematic flow of interactions is shown in Fig. 1. Parameters c and b represent the global balance between excitation and inhibition within a single oscillatory unit (Koppert et al., 2014). Depending on these parameters, the unit can be in a steady state, a limit cycle or both (bistability).

Figure 1.

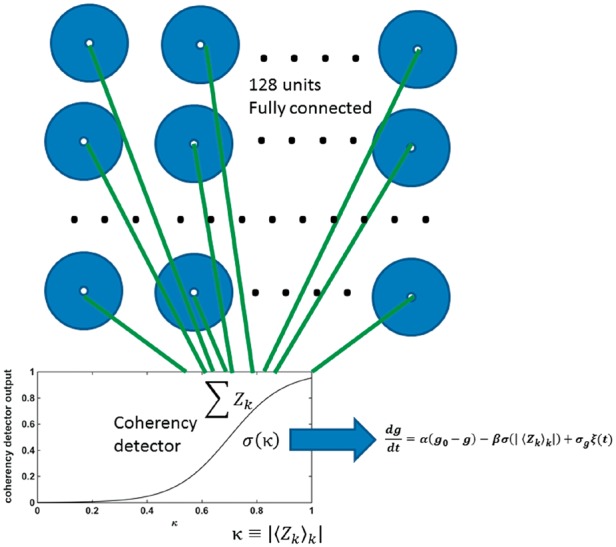
Schematic representation of the model neuronal network. The model consists of 128 fully interconnected units, representing neuronal lumps including pyramidal neurons and interneurons. Any two units are equally interconnected. The collective output of all units is filtered through a sigmoid function or coherency detector (input-output function in inset and Equation 2). The horizontal axis represents the collective output of the model, the vertical axis is the detector response. The output of the coherency detector is used as input for the dynamics of the connectivity parameter g, which is common for all units.

We selected the parameters ($c=-2.26,\hspace{0.5em}b=3,\hspace{0.5em}\omega =0$?>) such that each individual unit is in one state—that of a fixed point harmonic oscillator (normal, non-seizure state). The behaviour of the connected system is therefore a collective emergent property, influenced by the connectivity strength determined in parameter g.

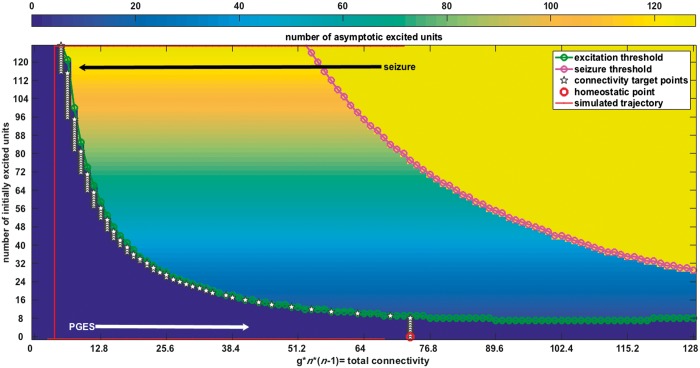
We carried out two series of model simulations. First, a series of simulations for an array of units with different levels of connectivity [range (0,1/128), 101 values] was done under stationary parameters without external input or noisy perturbations. The purpose of these ‘stationary state’ simulations was to explore the diversity of asymptotic states of the model, depending on the connectivity parameter g and the initial conditions. For each connectivity value, 129 simulations were performed with increasing numbers of units (from 0 to 128) in an activated state of limit cycle as initial condition. The connectivity matrix for all simulations in this study was chosen arbitrarily $C_{mk}=1,\hspace{0.5em}m\ne k,\hspace{0.5em}{C}_{mm}=4\hspace{0.5em}$?> to represent the relative difference in local versus global connectivity.

The second series of simulations was performed to obtain dynamical seizure transitions and postictal states. Noise was added to the system, and a parameter evolution rule was introduced, consisting of negative feedback plasticity that drives the connectivity parameter g to lower values whenever the global synchronized activity of the system exceeds a threshold (Equation 2). In addition, homeostatic point stochastic dynamics were introduced for the parameters b and c to account for random-walk type of fluctuations of the operational point of the model.

$$\frac{dg}{dt}={\alpha }_g\left(g_0-g\right)-\beta \sigma \left(\left|\hspace{0.5em}\text{〈}{Z}_k\rangle {}_k\right|\right)+{\sigma }_g\xi (t)$$

$$\frac{dc}{dt}={\alpha }_c\left(c_0-c\right)+{\sigma }_c\mu (t)\hspace{0.5em};$$

$$\frac{db}{dt}={\alpha }_b\left(b_0-b\right)+{\sigma }_b\nu (t)\hspace{0.5em}]$$

$$\sigma (x)\equiv \raisebox{1ex}{$e^{\frac{x-x_0}{s}}$}\!\left/ \!\raisebox{-1ex}{$(1+e^{\frac{x-x_0}{s}})$}\right.$$ (2)

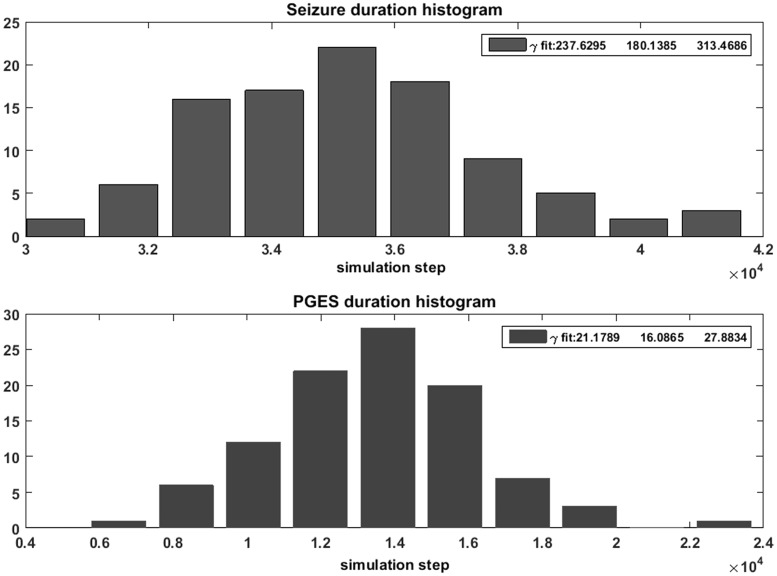
In Equation 2${\alpha }_g\hspace{0.5em}$?> and $\beta$?> are rate constants that determine the relaxation of the g-parameter and its corresponding reaction to increased coherency between the units. ${\alpha }_c\hspace{0.5em}$?> and ${\alpha }_b\hspace{0.5em}$?> are rate constants for the fluctuating {c,b}-parameters to a fixed homeostatic point $\left\{c_{0,}{b}_0\right\}=\left\{-2.26,\hspace{0.5em}3\right\}$?>. The second term in Equation 2 is a shortened version of an external unit, that according to previous results, can be activated by the network when the phase coherency of the system exceeds a certain level (Koppert et al., 2014). The last terms $\xi \left(t\right),\mu \left(t\right),\nu (t)\hspace{0.5em}\hspace{0.5em}$?> in Equation 2 represent noise and are independent random variables with normal distributions of unit variance. To reduce the complexity of the model we emulated the activation process by an effective sigmoid function, as defined by the last line of Equation 2. We performed 100 simulations initializing the system with all units having positive real values of >1. This started the simulation with the system in a limit cycle with all units recruited, i.e. a ‘seizure’. We recorded the time (number of simulation steps) it took for the limit cycle (‘seizure’) to be destroyed by the change in connectivity g and the time it took to return to a level of excitability in the ‘normal’ range, which we defined as an excitability threshold 50% higher than that of the homeostatic point. This was used as an estimate of the duration of the model postictal period reflecting PGES (Fig. 2).

Figure 2.

Output from the computational model. Results from simulations of the system (Equation 1). The system output is generated for 129 values of the connectivity parameter g, ranging from 0 to 128 on the horizontal axis, and for 0 to 128 initially excited units, indicated on the vertical axis. The background colour represents the number of excited units that remain self-sustained according to the dynamics of the coupled system of oscillators. All simulations were first done without noisy input and without changes of the connectivity parameter g. The blue region corresponds to a non-excitable state (‘postictal’); yellow to a limit cycle state (total synchronization or ‘seizure’); and the gradually coloured state in the middle, to ‘normal functioning’, where the system sustains its initial state. Introduction of noise and plasticity of connectivity g through the coherence detector (Equation 2), makes the system transition between the different states (red line). The model simulation starts in a ‘seizure’ state. The connectivity parameter g is activated above a certain level of synchrony (the input from the coherency detector from Fig. 1). This ‘seizure’-induced plasticity of the connectivity parameter g causes termination of the ‘seizure’ and drives the return through a ‘postictal’ period to the ‘normal’ state which we defined as an excitability threshold 50% higher than that of the homeostatic point, indicated in red.

For this second set of simulations we chose $\left\{{\alpha }_g,{\alpha }_c,{\alpha }_b\right\}=0.002,\hspace{0.5em}\hspace{0.5em}\beta =0.007\hspace{0.5em}$?>$g_0=0.0045,x_0=0.1$?> and s = 0.05, which provided a single homeostatic point. The simulations were done with noise levels of ${\sigma }_z=3,\hspace{0.5em}{\sigma }_c=2,{\sigma }_b=2,\hspace{0.5em}{\sigma }_g=0.02$?>.

Statistics of state durations

It was previously shown that differences in the distributions of durations between stable and transient states can be revealed using a gamma-type probability density function as a fitting template (Equation 3) (Suffczynski et al., 2006; Colic et al., 2013).

$$\text{N}(T)=N_0{T}^{\text{α}-1}{e}^{-\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$\text{β}$}\right.}$$ (3)

Where $\hspace{0.5em}{N}_0\hspace{0.5em}$?> is the normalization constant, β is the time-decay constant and α is the shape parameter, which separates random from deterministic processes. In short, α ≤ 1 is expected for the distribution of stochastic processes (α = 1 corresponds to a Poisson process), while α > 1 may be a consequence of a process with deterministic state-termination mechanism (Doob, 1953; Suffczynski et al., 2006).

To study the dynamics underlying the transitions in our model, we simulated 110 ‘seizures’ followed by 110 model ‘postictal’ periods. The segmentation of these epochs was performed using the thresholds of the envelope of the averaged signal from the unit output.

Human EEG recordings

We screened the video-EEG reports of subjects aged >15 years who underwent presurgical evaluation at a tertiary referral centre and selected those that mentioned the recording of a convulsive seizure. Only the first convulsive seizure recorded from each individual was selected to avoid effects of seizure clusters. For most, anti-epileptic drugs were tapered during the recording to maximize the likelihood of an ictal recording. In view of the changes to anti-epileptic drug regimens, we chose not to include periods between two seizures.

In total, 56 convulsive seizures were identified. One recording was excluded due to insufficient postictal recording time and two due to inadequate EEG quality. Data from this database were published previously (Lamberts et al., 2013a, b). From the 53 remaining recordings, convulsive seizures with an asymmetric partial ending (unilateral clonic movements and/or partial epileptic activity, four seizures) or convulsive seizures ending with generalized activity without convulsive movements (one seizure) were excluded, leaving 48 seizures. Subject characteristics are shown in Table 1.

Table 1.

Subject characteristics

	PGES+	PGES–	Test
Variables	n = 37	n = 11
Gender
Male (%)	20 (54)	8 (73)	F, P = 0.319
Female (%)	17 (46)	3 (27)
Age at time of EEG, years, median (range)			MW, P = 0.081
	36.1 (15–61)	28.3 (16–43)
Duration of epilepsy, years, median (range)			MW, P = 0.581
	18.4 (2–46)	21.3 (4–42)
Epilepsy classification
Symptomatic (%)	27 (70)	11 (100)	F, P = 0.089
Cryptogenic/idiopathic (%)	10 (30)	0 (0)
Ictal EEG onset
Temporal (%)	18 (49)	5 (45)	F, P = 1.00
Extra-temporal (%)	19 (51)	6 (55)
Frequency of CS
1–2 CS/year (%)	20 (54)	5 (45)	F, P = 0.736
>3 CS/year (%)	17 (46)	6 (55)
Total duration of seizure			MW, P = 0.573
S, median (range)	122.3 (63–444)	221.2 (45–828)
Duration of TC phase			MW, P =0.202
S, median (range)	66.01 (32–118)	73.8 (36–100)
Duration of PGES
S, median (range)	55.7 (2–252)	NA

F = Fisher’s exact test; MW= Mann-Whitney U-test; TC = tonic clonic; CS = convulsive seizure.

The scalp EEG recordings used the international 10%–20% system at a sampling rate of 200 Hz (Stellate Harmonie, Stellate Systems).

Two experienced clinical neurophysiologists (R.D.T., D.N.V.) independently marked the start of the seizure, the tonic phase, the clonic phase, the end of the seizure, and the start and end of PGES periods. These were defined as periods immediately postictal (within 30 s), with generalized absence of electroencephalographic activity >10 µV in amplitude, allowing for muscle, movement, breathing and electrode artefacts (Lhatoo et al., 2010). All PGES periods longer than 1 s were scored (Surges et al., 2011).

The beginning and end of every epileptic discharge (on the EEG) and corresponding artefact of the clonic movement verified with video (‘clonic discharge’) was marked in the EEG by an observer (P.R.B.) who was not a neurophysiologist and as such effectively blinded for the presence of PGES, as the distinction of artefacts and real activity in EEG is difficult to the untrained eye. The EEG signal was visually inspected using a 0.3 Hz low-pass and 35 Hz high pass filter. Sensitivity was 5–7.5 µV and a longitudinal bipolar montage was used (‘double banana’).

The time of the markers was imported in Matlab® (release 2014b, The MathWorks Inc., Natick, MA, USA). The difference between the onset of each two adjacent ‘clonic discharges’ was calculated in milliseconds.

EEG analysis

The change in clonic frequency in the EEG was quantified by fitting a linear equation to the logarithm of the interclonic interval. If the times of successive clonic discharges for a given seizure are t_k (marked by visual inspection of the EEG traces), then exponential slowing down can be formulated as (Equation 4)

$$IC{I}_k\equiv t_{k+1}-t_k=C_0{e}^{a\hspace{0.5em}{\tau }_k};{\tau }_k\equiv \raisebox{1ex}{$\hspace{0.5em}(t_{k+1}+t_k)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$ (4)

The linear fit between the logarithm of the interclonic interval and the middle time of the interval between each two successive clinic discharges ${\tau }_k$?> provides the quantity that characterizes the decrease of the rate of ‘clonic discharges’.

$$\log \left(ICI\right)\approx a{\tau }_k+\log \left(C_0\right)+\varepsilon$$ (5)

In Equation 5 the fitting parameters and $\log \left(C_0\right)$?> are obtained using the standard MatLab fitting routine polyfit applied to linear order (n = 1). The last term in Equation 5 is a random variable representing the deviation from the fit. Its variation $r=var\left(\varepsilon \right)\hspace{0.5em}$?> is the residual variance after the fit. The residual variance was used to estimate the ‘goodness of fit’ (GOF) of the exponential fit. From Equation 5 it follows that

$$var\left(\text{log}\left(ICI\right)\right)\approx \frac{var\left(ICI\right)}{ICI}=var\left(\varepsilon \right)=r;\hspace{0.5em}GOF\equiv 100\left(1-r\right);\hspace{0.5em}$$ (6)

The total effect of ictal slowing for each seizure is quantified as

$$IC{I}_{terminal}\equiv C_0{e}^{a\hspace{0.5em}{T}_{seizure}}$$ (7)

In the above definition the $C_0$?> and a parameters are derived for each case from the linear fit procedure in Equation 5, and $T_{seizure}$?> is the total duration of the seizure. The actual values of the first and last interclonic interval measured experimentally are influenced by noisy perturbations. We therefore use the projected terminal interclonic interval values assuming that the noisy component, ɛ, in Equation 5 has been largely filtered out by the fitting procedure. We call the quantity defined in Equation 7 projected terminal interclonic interval (ICI_terminal).

To test whether the PGES durations (set to zero if no PGES is detected) $\left\{T_{PGES}\right\}\hspace{0.5em}$?> and the corresponding $\left\{IC{I}_{terminal}\right\}\hspace{0.5em}$?>of the convulsive seizure are functionally related, we used the unidirectional $h^2$?> non-linear association measure (Kalitzin et al., 2007). The association index estimates the variance of one time series, x, that can be explained by the variance of a second time series, y, and in this way quantifies the exactness of the best functional map between the two time series.

$$h^2\left(x,y\right)=1-\frac{var(x|y)}{var(y)}$$ (8)

The unidirectional nature of the index Equation 7, [or the non-symmetric relation $\hspace{0.5em}\hspace{0.5em}{h}^2\left(x,y\right)\ne h^2\left(y,x\right)$?>], reflects the fact that not all functions are invertible. A surrogate-based test that establishes the statistical significance of the $h^2$?> index was derived (i.e. estimates the probability of obtaining the given association index by chance). In the present study we chose the number of bins, the only instrumental parameter needed, as 10. For the statistical significance validation of the associative index, we applied 100 000 surrogate tests. The distributions of the ICI_terminal quantities ρ from Equation 7 and the GOF values from Equation 6 as functions of the PGES duration were estimated. The set $\left\{T_{PGES}\right\}$?> was divided into bins with unequally spaced borders at 0, 10, 50, 100, 200 and 500 s. Significant differences in the corresponding distributions were detected using the non-parametric Kruskall-Wallis test.

Results

Characteristics of the neuronal mass model under stationary parameters

To elucidate the type of dynamics underlying seizure termination and PGES, we created a computational model, which we first analyzed under stationary parameters. The entire system has three different dynamic regimes depending on the connectivity g, shown in Fig. 2 (Koppert et al., 2014). For lower values of g the system is not excitable. This state represents PGES, as an extreme of the postictal state (blue region on the left in Fig. 2). For higher values of g, the system is in a stable state depending on the initial conditions or external perturbations. This represents normal brain functioning. Finally, when g is large, the system has only one asymptotically stable state (attractor), which is a limit cycle of all units oscillating synchronously, representing an epileptic seizure. We reproduced the above model in the interaction term as previously with only the real components of the units (Koppert et al., 2014). Each individual unit has one state (embedded properties), while the system of connected units can have different states. We identify these states and the transitions between them as ‘emergent properties’ of the model.

Characteristics of the neuronal mass model with activity-dependent plastic feedback parameter dynamics

To make the model transition autonomously between seizures, postictal periods and normal periods, we introduced random noise and a negative feedback plasticity rule that drives the connectivity g to smaller values whenever the global synchronized activity of the system exceeds a certain threshold (Equation 2). When random fluctuations bring the system above the ‘recruitment threshold’, the system enters full synchrony or a ‘seizure’ state. Figure 2 shows a simulated trajectory (red line with arrows) as an example of a succession of these dynamic states: from the seizure state and to the non-excitable postictal state and back to the normal state. The transition to the postictal state is determined by the influence of the connectivity change (Equation 2) causing a transition to a temporary state of low inter-unit connectivity, with low values of the connectivity parameter g, where the system is silent and non-excitable. The connectivity then gradually increases again until the system is in its normal state. The system stays in its homeostatic domain (‘normal operation’) most of the time, but it can make a transition to a fully synchronized state (‘seizure’) because of external input or random noise fluctuations exceeding the recruitment threshold.

Predictions about seizure termination according to the neuronal mass model

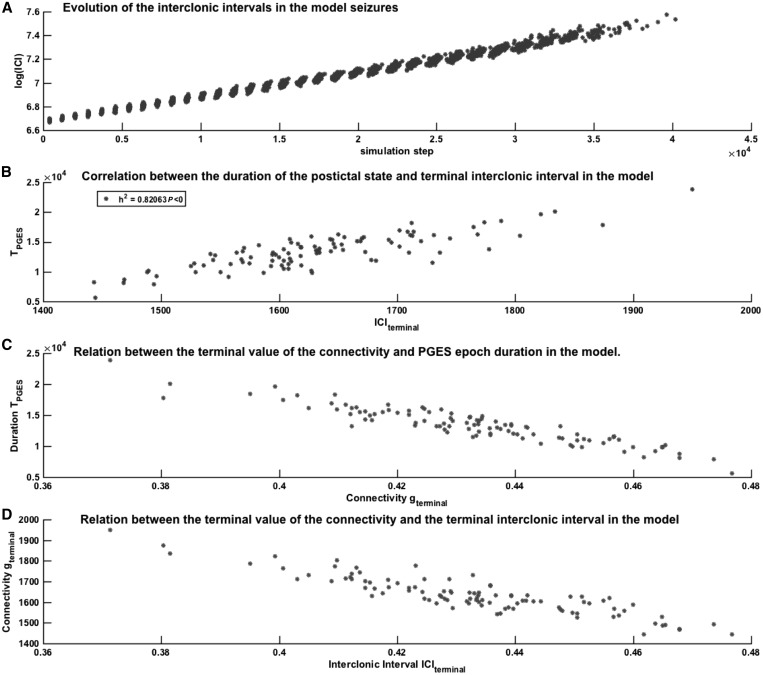
Our computational model has three essential features that were used to analyze the human EEG data of convulsive seizures. First, the shapes of the distributions and the parameter values suggest that the duration of the ‘ictal’ [α = 237.6, 95% confidence interval (CI) 180.1–313.5] and ‘PGES’ (α = 21.2, 95% CI 16.1–27.9) epochs have deterministic properties. In Fig. 3, the distributions of the epoch lengths and their corresponding gamma-distribution fits are shown. This leads to the first hypothesis (Hypothesis 1): the durations of the convulsive seizure and PGES events in humans display distributions corresponding to deterministic termination processes. The second feature of the model is that seizure termination is influenced by the connectivity parameter g. This suggests the existence of a measurable quantity, reflecting changes in connectivity, which changes during a seizure until its termination. In our model, we coupled the evolution of connectivity parameter g to the global level of synchronization of the system as expressed in the first line of Equation 2, enabling the measurement of the interval between modelled clonic bursts or interclonic interval. Figure 4A shows that the interclonic interval increases as a function of the time elapsed from the start of the seizure. The connectivity changes exponentially as the seizure progresses [log(interclonic interval) ∼ time], and the terminal value of the interclonic interval correlates strongly with the duration of the ‘PGES’ state in the model (Fig. 4B, h² = 0.82). Figure 4C shows the relation between connectivity parameter g and PGES duration, and between the terminal interclonic interval and the terminal value of g (Fig. 4D). It was previously observed that interclonic intervals increase in a logarithmic fashion [i.e. interclonic interval ∼ log(time)] towards the end of a convulsive seizure (Jirsa et al., 2014). Our second hypothesis (Hypothesis 2), derived from our model and from clinical observations is that the interclonic intervals increase exponentially towards the end of the seizure (Conradsen et al., 2013; Beniczky et al., 2014). This may be an epiphenomenon of the decrease of the connectivity g facilitating the termination of the seizure in the model. Lastly, our third and most important hypothesis (Hypothesis 3) is that the interclonic interval at the end of a convulsive seizure is associated with the duration of the following PGES period. This is motivated by the observation in our model that the dynamics of the connectivity parameter g during a seizure are involved in seizure termination and lead to a ‘PGES’ state of suppressed activity (Fig. 2). The duration of this period is determined by the time needed for the connectivity parameter g to re-enter the normal operational state. In the absence of noisy input, this time depends on the value of the connectivity parameter g when the seizure terminates. Accordingly, the model shows that the duration of the postictal period is related to the connectivity parameter at the end of the seizure reflected by the oscillatory frequency of the model, which, in Hypothesis 2, corresponds to the interclonic interval.

Figure 3.

Gamma distributions of ictal, postictal and normal period durations in the model. Histograms and fitted gamma functions for the distributions of the ‘seizure’ (top) and ‘postictal’ (bottom) durations as simulated using the model. The estimation of the shape parameter α for the fitted gamma-distribution as well as the 95% CIs are presented in the text boxes. The data were obtained using the standard MatLab® function gamfit.

Figure 4.

Relation between the interclonic interval, connectivity and PGES in the model. (A) Scatter plot showing the relation between the ICI (vertical axis, logarithmic scale) determined by the strength of the connectivity parameter g during simulated seizures and the time elapsed since the beginning of the simulated seizure (horizontal axis, in simulation steps). The different data points at each time point represent different simulations. The figure shows that the interclonic interval is relatively constant at the start of the model seizure, but varies at the end of the seizure. (B) The relation between the model terminal interclonic interval (ICI_terminal, horizontal axis) value and the duration of the PGES state in the model (vertical axis). The non-linear correlation coefficient h² shows that the terminal interclonic interval value explains 82% of the variability of the PGES duration. (C) Scatter plot showing the relation between the durations of the simulated PGES states (vertical axis, in simulation steps) and the value of the connectivity parameter g at the end of the preceding seizure (horizontal axis, dimensionless units). (D) the relationship between the terminal value of the connectivity parameter g and the terminal interclonic interval in the model.

In the next section, these three features deduced from our neuronal model are tested in human EEG recordings of convulsive seizures.

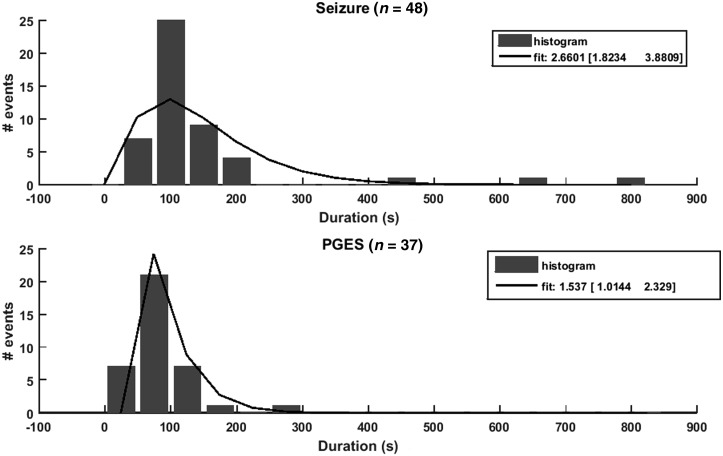
Gamma distribution of human seizure and PGES durations

Of the 48 convulsive seizures, 37 ended with PGES (Table 1). Analogous to the model data, the duration of the seizures and PGES periods was assessed. The distribution of the durations and corresponding gamma-distribution fits are shown in Fig. 5. The seizure duration varied from 45 to 828 s and PGES periods lasted 2 to 252 s. The distribution of the durations of PGES (α = 1.537, 95% CI 1.014–2.32) in human EEG suggests a deterministic process. We confirm previous observations of a deterministic process probably underlying convulsive seizure duration (α = 2.660, 95% CI 1.823–3.880). Both findings are in line with Hypothesis 1 from the model.

Figure 5.

Gamma distribution of ictal and PGES period durations in human EEG data. Histograms and fitted gamma functions (solid lines) for the distributions of the seizure (top) and PGES (bottom) durations as visually detected from the human EEG recordings. The three numbers in the legends give the parameter α (from Equation 3) for the fitted gamma-distribution and the corresponding 95% CI as obtained from the standard MatLab® function gamfit.

Clonic slowing at the end of a convulsive seizure follows an exponential pattern

The convulsive seizures in our sample ended with a clonic frequency between 0.5 and 1.5 Hz, estimated by visual inspection of EEG traces of epileptic discharges and video recordings of corresponding clonic movements (‘clonic discharge’). The clonic frequency decreased exponentially in most seizures. Examples of the linear fit of the logarithm of the interclonic interval from single seizures, as a function of time from clonic phase start, are shown in Fig. 6. The averaged goodness of fit for all 48 convulsive seizures was 73%, with standard deviation 14%. This validates Hypothesis 2 from the model. We compared the exponential fit of the interclonic intervals in our sample of 48 seizures to the logarithmic fit previously reported (Jirsa et al., 2014) and to a power law fit. The results are shown in Supplementary Figs 1–3. The systematic errors of these three fits were similar. The Wilcoxon signed rank test showed that in our sample, the exponential fit was equal to the power law fit, but explained the clonic slowing down better than the logarithmic fit, even if by a moderate margin (Supplementary Fig. 4).

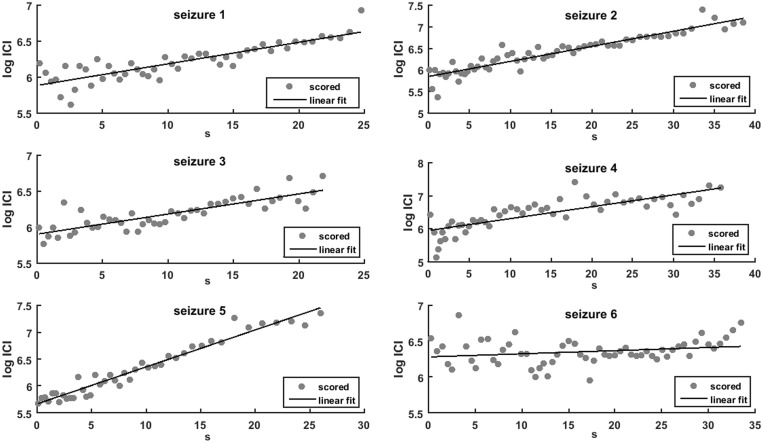
Figure 6.

Linear fit of the interclonic interval in human seizures. Scatter plots of interclonic intervals (circles) and best linear fit (solid line) between the time from the beginning of the convulsive phase (in seconds, horizontal axis) and the logarithm of the interclonic intervals [log(ICI), vertical axis]. The figure illustrates the six first seizures from the dataset, the fitting algorithm was applied to all 48 cases.

Clonic slowing is associated with PGES duration

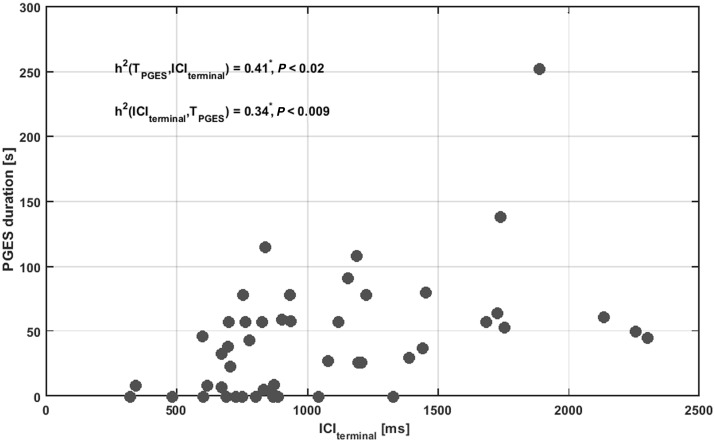
The exponential fit of clonic slowing was used to estimate the terminal value of the connectivity parameter at the end of real seizures, in analogy with the model. This value (projected terminal interclonic interval, ICI_terminal) was then correlated with the occurrence and length of PGES. A scatter plot depicting the ICI_terminal and PGES lengths is shown in Fig. 7. If there was no PGES the value of PGES was set to zero. ICI_terminal explained 41% of the variance in PGES duration: h² = 0.41, P < 0.02. PGES duration explained 34% of the variance in ICI_terminal: h² = 0.34, P < 0.01 (Fig. 7). This is in keeping with Hypothesis 3, that the ICI_terminal, possibly reflecting the decrease in connectivity, is correlated with PGES occurrence and duration. The larger the total deceleration effect, the longer PGES lasts. Several seizures in our sample with a marked interclonic interval increase, however, did not end with PGES, but there were no seizures without interclonic interval increase that ended with PGES. This makes clonic slowing a highly sensitive predictor of PGES in our data sample. The strongest association is seen between clonic slowing leading to a long ICI_terminal and long PGES. The goodness-of-fit increased when seizure termination is followed by a longer PGES period. This corroborates with Hypothesis 3, i.e. that deterministic dynamics, typical of long ICI_terminal, also determine the presence and duration of PGES. In line with previous studies (Lhatoo et al., 2010; Surges et al., 2011; Semmelroch et al., 2012; Seyal et al., 2012), there was no correlation between the duration of the seizure and the ICI_terminal in our sample (h² = 0.15, P = 0.46).

Figure 7.

Relation between interclonic interval and postictal period duration in EEG recordings. Scatter plot showing the relation between the terminal interclonic interval (ICI_terminal) values (in milliseconds, horizontal axis) and PGES duration (in seconds, vertical axis). Convulsive seizures that were not followed by a PGES event were accounted as 0 s. The non-linear association index h² was determined and shows a relatively small, but statistically significant functional relation (P < 0.05, indicated by an asterisk) between PGES duration and ICI_terminal in both directions.

Discussion

We combined computational modelling and human EEG recordings of convulsive seizures, to show that (i) probability distributions of the durations of ictal and postictal periods are indicative of deterministic processes; (ii) the interclonic interval increases in an exponential manner during human seizures, which is in accordance with the model and may reflect a decrease in neuronal network connectivity that in our model leads to seizure termination and PGES; and (iii) the projected terminal interclonic interval (ICI_terminal) is associated with the occurrence and duration of PGES. The results are in agreement with the hypothesis that a neuronal mechanism that underlies transitions from ictal to postictal and from postictal to normal states may be activated in response to total synchronization during a convulsive seizure.

Gradual slowing of epileptic bursts and clonic frequency towards the end of seizures is frequently observed, but not fully understood (Panayiotopoulos et al., 2010; Truccolo et al., 2011; Conradsen et al., 2013). Our findings suggest that this phenomenon may be related to plastic changes in functional connectivity. Several studies report on dynamical changes during the ictal state. Animal models of focal epilepsy have shown that the excitatory-inhibitory balance changes during a seizure, in line with the dynamics in our study (Žiburkus et al., 2013; Boido et al., 2014). Towards the end of a seizure, both excitatory and inhibitory neuron populations become increasingly active; this may lead to increased burst activity and longer interburst intervals (Boido et al., 2014). Interneurons also receive strong excitatory input, leading to continuous activation of the inhibitory inputs to pyramidal cells, and seizure termination (Žiburkus et al., 2013). Recent studies showed changes in high-frequency oscillatory dynamics and increased spatial and temporal correlation in human EEGs during the ictal state, providing additional evidence for plastic changes towards the end of a seizure leading up to seizure termination (Kramer et al., 2012; Stamoulis et al., 2013).

Transitions from ictal to postictal states are clinically important in view of SUDEP following PGES and status epilepticus. Cardiorespiratory mechanisms, possibly mediated by brainstem dysfunction were suggested to play a role in SUDEP (Ryvlin et al., 2013; Mueller et al., 2014; Aiba and Noebels, 2015). The successful modelling of the transition from ictal to postictal state in our neural mass model suggests that a PGES state can be caused by neuronal mechanisms, although other factors may contribute. Neuronal exhaustion was previously suggested as a possible mechanism of PGES, but seizure duration as such, was not associated with PGES in our sample and others, making neuronal exhaustion an unlikely cause of seizure termination and PGES (Lhatoo et al., 2010; Surges et al., 2011; Semmelroch et al., 2012; Seyal et al., 2012; Freitas et al., 2013; Lamberts et al., 2013a, b). It is possible that several pathways lead to PGES: in addition to EEG suppression induced by diffuse cortical inhibition, EEG suppression can also be induced by hypoxia, hypotension and asystole, which may all occur in the postictal state (Surges and Sander, 2012; Bozorgi et al., 2013; Moseley et al., 2013; Ryvlin et al., 2013; van Dijk et al., 2014; Massey et al., 2014).

Our results show characteristics of global seizure dynamics, but cannot exactly predict what neurophysiological substrate causes both seizure termination and PGES. A variety of different mechanisms and mediators may be involved, such as adenosine and potassium. An in vitro study showed that synchronous high-frequency firing of neurons, analogous to the ictal state, causes release of adenosine (Lovatt et al., 2012). In vivo, adenosine concentration rises sharply during the last phase of a seizure in swine and humans, reaching a maximal level after seizure termination (Van Gompel et al., 2014). A model in which the transition from high frequency to low frequency discharges in the course of a seizure is mediated by an increase in the Ca-dependent K⁺ current, leading to an increase of extracellular K⁺ has been proposed (Somjen et al., 2008). The authors show that an overload of [K⁺]_o can initiate spreading depression, and thus termination of seizure discharges (Somjen et al., 2008). Another computational study linked seizure termination and postictal depression to the complex interaction between sodium, potassium and chloride concentrations (Krishnan and Bazhenov, 2011). These two studies demonstrate processes at a microscopic level, which are analogous to the transition from seizure to PGES at a macroscopic level that we describe. These processes may account for the reported decrease of functional connectivity and excitability. The translation from the microscopic level of modelling to the macroscopic level is a matter of further study. Further investigations are needed to determine the exact role of these processes in causing seizure termination and PGES in vivo. We hypothesize that a neuronal seizure termination mechanism serves to restore normal function and to protect the brain from damage arising from neuronal exhaustion and metabolic depletion. Such a mechanism may also prevent status epilepticus or seizure clusters. If this ‘neuronal emergency brake’ is activated too strongly or persistently, PGES occurs.

Excessive clonic slowing in relation to PGES may be considered a feature of a critical transition, in line with observations of slowing as a generic feature and possible early warning signal in systems approaching a critical transition or ‘tipping point’ (Scheffer et al., 2009). Our finding that PGES was always preceded by a marked exponential decrease of clonic frequency is important as it may lead to the development of an algorithm for real-time anticipation of potentially fatal seizures using motion-detection sensors, including remote video detection (Kalitzin et al., 2012, 2016).

Any computational model of complex systems as the human brain can only account for a limited number of properties. Our model is an abstract representation of neuronal dynamics. It is, however, capable to predict relevant phenomena, such as the gradual change of the ictal state towards its termination. When using computational models it is essential to distinguish between ‘embedded’ (created and pre-tuned) and ‘emergent’ (predictive) properties of the model. In our model, the oscillatory state of the individual units is embedded, while the collective dynamics and the transitions between states are emergent properties, with potential predictive value. We consider the existence of oscillatory states, interpreted as model seizures and their deterministic termination mechanism as a built-in property. The existence of ‘PGES’ states and their transient dynamics, however, are emergent properties of the collective system dynamics. The same holds true for the association between the duration of the PGES state and the value of the connectivity parameter g at seizure termination. These emergent properties can be qualitatively explained by the phase-space structure shown in Fig. 2, which can be interpreted as an emergent property in its entirety as it cannot be reduced to the dynamics of the individual units. The predictive power of our model is also due to its autonomous nature. Many computational models of the epileptic condition require the adjustment of their parameters in order to change behaviour from ‘seizure’ to ‘normal’. Such models can describe the individual states but will not provide predictions, or emergent features, from the dynamics of the transition between those states. Our model describes the transitions from ictal to postictal and back to a normal state as an autonomous process without any predefined parameter alterations. The only precipitating factor affecting the deterministic transitions is the stochastic noise present in the system. Parameter and dynamic variables fluctuations alone would result in random-walk type transitions that are described by gamma distributions with α ≤ 1. The case α = 1, or Poisson distribution, is characteristic for random transitions with no memory from the past states while α < 1 represents the more realistic case where the system may still float away from the transition region. A deterministic component that introduces an additional time scale would result a shift of the α parameter to α > 1 values. We did not provide simulation results with various mixing levels of stochasticity versus determinism as this was not the primary objective of our study. The validation of the hypotheses generated by our model with the human data is not a claim of uniqueness of the model but a consistency check. Indeed, any distribution on the positive time axis can be represented as a superposition of an infinite number of exponential functions (Laplace representation) and a (normalized) superposition of exponential distributions, possibly due to a decay process of a multistate system, may also result in a gamma fit with α > 1.

Other types of plastic change may exist in addition to the plasticity of the connectivity parameter we used in the model. We tested several types of plasticity mechanisms, affecting either the unit excitability or the inter-unit connectivity or both. All lead to (i) deterministic seizure termination; and (ii) a transient postictal state with suppressed activity and excitability. In all cases, the duration of the postictal supressed state was associated with the terminal value of the plasticity parameter. It is, however, the particular choice of Equation 2 and the interaction term in Equation 1 that relates the interclonic interval increase during the seizure to the change in connectivity parameter g. Other parameter choices did not produce the same effect. Our model may be used as a starting point to reconstruct the exact properties of the mechanism of seizure termination, using a more detailed model. Our results may not apply to all seizure types. A different type of model, for example, predicts a logarithmic [ICI ∼ log(t)] evolution of the interclonic intervals preceding a homoclinic bifurcation at seizure offset (Jirsa et al., 2014). It was validated in a clinical sample, which does not appear, however, to have been selected based on the same seizure criteria as ours (see ‘Materials and methods’ section). The underlying pathophysiological mechanisms of seizure termination may therefore differ. Interestingly, in our sample the systematic errors of the logarithmic and power law fits differed little from the exponential fit (Supplementary material). Fits based on exponential equations were previously rejected as they can underestimate the interspike interval near the end of seizures and, in certain models, predicted that spikes would continue after the end of the seizure (Jirsa et al., 2014). In our model the parameter evolution law of connectivity parameter g is only valid during the seizure periods; thus our model did not predict that spikes continue after seizures termination. The exponential fit also did not underestimate the terminal value of g linked to the interclonic interval, and correlated with the duration of subsequent PGES. The exponential law is covariant with the reference time, as $IC{I}_t=IC{I}_u{e}^{t-u}=IC{I}_0{e}^t,\hspace{0.5em}IC{I}_0=IC{I}_u{e}^{-u}$?>. The log(t) evolution, however, depends on the exact determination of seizure termination time. If the interclonic intervals are increasing exponentially towards the end of the seizure, their inverse, the instantaneous clonic frequency F = 1 / ICI is decreasing exponentially. We confirmed this hypothesis in a recent study using optic flow video sequences (Kalitzin et al., 2016).

Previous work showed that the probability distribution of the duration of absence seizures in humans and rodent and computational models of epilepsy can, in some cases, also follow a stochastic pattern (Suffczynski et al., 2006). This suggests that the termination mechanism may be defective in certain circumstances, causing seizures to terminate due to random fluctuations.

A computational model is a homogeneous system. We validated its predictions using seizures recordings from different individuals, in whom different mechanisms may contribute to seizure termination. This probably explains the difference in strength of the association between the last interclonic interval and PGES in the model and in humans. Ideally, a large number of seizure EEG recordings from the same individuals would be needed to confirm this hypothesis.

The sample size of our human EEG data is limited and surface EEG for postictal assessment presents some drawbacks. Artefacts (e.g. nursing interventions, muscle activity and breathing activity) may have contaminated the EEG, thereby preventing precise estimation of PGES duration. Despite being a well-defined neurophysiological state that is easier to quantify than postictal slowing in general, PGES duration is inevitably a semi-exact outcome measure. One way to circumvent this is to use intracranial EEG recordings, but because of sparse spatial sampling this will lack a global measure of cortical activity. In our subjects, anti-epileptic drugs were tapered in the course of seizure monitoring. Such tapering may increase the occurrence of PGES (Lamberts et al., 2013a), and may theoretically alter mechanisms of seizure termination.

Our study demonstrates the power of combining computer modelling and neurophysiological observations to formulate testable hypotheses leading to new approaches to elucidate epileptic seizure mechanisms in human EEG data.

Glossary

Abbreviations

ICI

interclonic interval

PGES

postictal generalized EEG suppression

SUDEP

sudden unexpected death in epilepsy