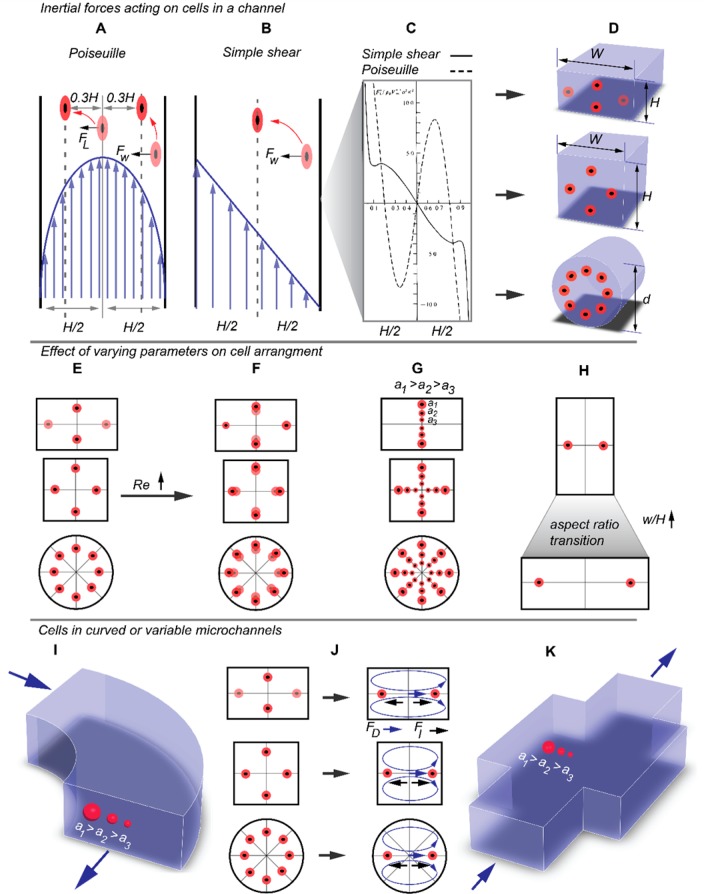
Figure 11.

Hydrodynamic effects on suspended cells in flow. (A) Cells in parabolic flow will be driven away from the center and the wall and find an equilibrium position at 0.3 H away from the center. (B) In simple shear flow, the only effect is the wall effect that drives the cells away from the wall until they find a stable position at the center. (C) Hydrodynamic forces acting on a particle in parabolic (dashed) and simple shear (solid) flow profiles. (D) Stable equilibrium positions for particles in an inertial Poiseuille flow in channels with different cross sections. (E and F) Effect of increasing Re on the stable positions for cells in channels with different cross sections. (G) Effect of the particle size on the inertial lift experienced by the particle. The larger the particle, the bigger the inertial lift forces, and as a result, the particle will find an equilibrium position closer to the walls. (H) Effect of varying the aspect ratio in the stable positions in a rectangular channel. (I) Curved microchannels result in cross-sectional, secondary flows around the bend, which affect the focusing of particles according to their size. (J) Secondary Dean flows occur as a result of mismatching fluid inertia along the curved channel and the resulting migration of the cells due to the interplay between the secondary flow drag force and the inertial lift forces. Two potential equilibrium positions in the vicinity of the inner and outer wall of the curve have been reported in the literature, with the inner wall position being the most frequently reported stable position for particles in curved channels. (K) Steps, converging-diverging channels, and wall irregularities will result in secondary Dean flow recirculation and, similarly to curved channels, induce a size-dependent separation of particles in the channel. (C) Reproduced with permission from ref (160). Copyright 1974 Cambridge University Press.