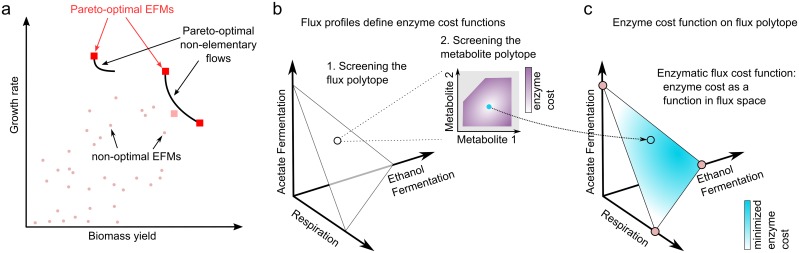
Fig 1. Rate/yield trade-offs and calculation of growth-optimal fluxes.

(a) Rate/yield spectrum of Elementary Flux Modes (EFMs) (schematic drawing). In the scatter plot, EFMs are represented by points indicating biomass yield and maximal achievable growth rate in a given simulation scenario. Pareto-optimal EFMs are marked by red squares. The set of Pareto-optimal flux modes (black lines) contains also non-elementary flux modes. An EFM may be Pareto-optimal when compared to other EFMs, but not when compared to all possible flux modes (e.g. the EFM below the Pareto front marked by a the pink square). Growth rate and yield are positively correlated in the entire point cloud, but the points along the Pareto front show a negative correlation, indicating a trade-off. (b) Enzyme cost of metabolic fluxes. The space of stationary flux distributions is spanned by three EFMs (hypothetical example). The flux modes, scaled to unit biomass production, form a triangle. To compute the enzyme cost of a flux mode, we determine the optimal enzyme and metabolite levels. To do so, we minimize the enzymatic cost on the metabolite polytope (inset graphics) by solving a convex optimality problem called Enzyme Cost Minimization (ECM). (c) Calculation of optimal flux modes. The enzymatic cost is a concave function on the flux polytope, and its optimal points must be polytope vertices. In models without flux bounds, these vertices are EFMs and optimal flux modes can be found by screening all EFMs and choosing the one with the minimal cost.