Signal competition in optical coherence tomography and its relevance for cochlear vibrometry

Abstract

The usual technique for measuring vibration within the cochlear partition is heterodyne interferometry. Recently, spectral domain phase microscopy (SDPM) was introduced and offers improvements over standard heterodyne interferometry. In particular, it has a penetration depth of several mm due to working in the infrared range, has narrow and steep optical sectioning due to using a wideband light source, and is able to measure from several cochlear layers simultaneously. However, SDPM is susceptible to systematic error due to “phase leakage,” in which the signal from one layer competes with the signal from other layers. Here, phase leakage is explored in vibration measurements in the cochlea and a model structure. The similarity between phase leakage and signal competition in heterodyne interferometry is demonstrated both experimentally and theoretically. Due to phase leakage, erroneous vibration amplitudes can be reported in regions of low reflectivity that are near structures of high reflectivity. When vibration amplitudes are greater than ∼0.1 of the light source wavelength, phase leakage can cause reported vibration waveforms to be distorted. To aid in the screening of phase leakage in experimental results, the error is plotted and discussed as a function of the important parameters of signal strength and vibration amplitude.

I. INTRODUCTION

The ability to make simultaneous measurements of the vibration of the cochlear partition's basilar membrane (BM) and tectorial membrane (TM) is vital to understanding the active, nonlinear mechanical processing leading to hair cell stimulation. However, currently the most common method for measuring vibration in the ear is heterodyne interferometry, built around a high-coherence helium neon laser, whose red light is not optimal for penetrating the organ of Corti complex (OCC). In addition, BM and TM vibration cannot be measured simultaneously with this technique since only the vibration of the surface that is in focus is measured. Spectral domain phase microscopy (SDPM), an extension of spectral domain optical coherence tomography (SDOCT) (Choma et al., 2005; Gao et al., 2013), is a recently developed technique that advances cochlear vibrometry. SDOCT uses infrared light to penetrate tissue, and low coherence interferometry to image structures beneath the tissue surface, and has been used to image the cochlea (Lin et al., 2008). Three groups with expertise in auditory mechanics and optics have developed SDPM to measure sound-induced vibration of the structures within the cochlear partition (Wang and Nuttall, 2010; Gao et al., 2013; Lee et al., 2015; Hong and Freeman, 2006). Other groups have used SDPM to measure middle ear motion (Chang et al., 2013). Petrie et al. (2013) described an analysis algorithm.

In this contribution we explore the similarity between SDPM and heterodyne interferometry, particularly as it informs our understanding of the problem of signal competition between nearby reflectors, termed “phase-leakage” in the SDPM literature (Ellerbee and Izatt, 2007). In past work, we described the signal competition problem of heterodyne interferometry, in which light returning from out-of-focus structures competes with light returning from the in-focus structure of interest, leading to erroneous reported vibrations (de La Rochefoucauld et al., 2005). Here we show that SDPM phase leakage is analogous to the signal competition artifact of heterodyne interferometry. We explore signal competition in SDPM with both theory, and measurements in the cochlea and a related test system.

II. ANALYTICAL BACKGROUND

A. Brief introduction to SDOCT imaging

Descriptions of SDOCT and SDPM can be found in the literature (Hendargo et al., 2011; Choma et al., 2005; Izatt and Choma, 2015). Here we provide the skeletal description needed for our purposes: exploring phase leakage in auditory measurements and illustrating the similarity between SDPM and heterodyne interferometry. SDOCT is based on spatial-domain Fourier analysis. The low-coherence light source encompasses a range of wavelengths, λ (or equivalently wavenumber, k = 2π/λ). The light is split into object and reference beams and after reflecting from the object and reference mirror, the beams are recombined and sent through a spectrometer, which disperses the light by λ, and then delivered to a linear array of photodetectors. The pattern of light on the photodetectors, intensity as a function of λ, is the raw data. This function of λ is analytically recast as a function of k. By taking the spatial Fourier transform of the k-domain function, the z-domain representation of reflectors in the axial (z) direction along the object beam path is found. The spatial Fourier transform of the k-domain pattern is a complex function of z. The magnitude of the z-domain function will contain peaks at the z indices of prominent reflectors. (For example, a prominent reflector at one position in z-space gives rise to a ∼sinusoidal pattern in k-space.) This z-domain representation is called an axial-scan, or A-scan (examples of A-scans in our data are in Figs. 2–5). An array of 1024 photodetectors will produce 512 z-indices, spaced by a distance that is set by the center wavelength λ₀ and bandwidth Δλ of the light source, found as Δz₀ = 2π/Δk = λ₀²/Δλ. We use a Thorlabs Telesto SDOCT system and its light source has Δλ ∼ 200 nm and λ₀ ∼ 1300 nm, which corresponds to Δz₀ ∼ 8.4 μm. However, this distance includes a factor of 2 for the back-and-forth of the object beam light, which is reflected from within the preparation, and the relevant spacing of adjacent z-domain indices, corresponding to the depth in the sample, is Δz = Δz₀/2 ∼ 4.2 μm. This expected spacing is close to the actual spacing in the Telesto system.

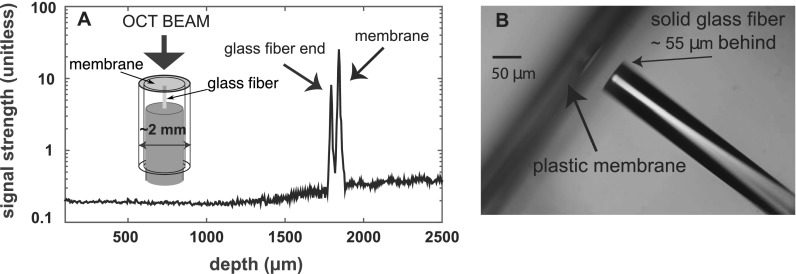
FIG. 2.

(A) A-scan of a sample composed of a transparent membrane ∼2 mm in diameter with a flat-tipped 125 μm diameter glass fiber ∼55 μm behind. Inset on the left is a sketch of the sample. (B) Microscope image of the sample.

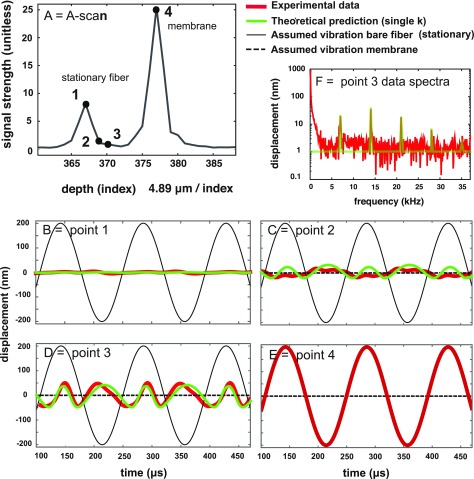
FIG. 3.

(Color online) Responses of the membrane/fiber sample when driven with a 7008 Hz pure tone of a level that resulted in a relatively large, but undistorted 200 nm vibration of the membrane [panel (E)]. (A) A-scan indicating the points of evaluation. (B)–(E) Thick red and mid-thickness green curves are, respectively, the reported and theoretical displacement responses. These responses are shown at the locations of the fiber and the membrane (prominent peaks 1 and 4) and two locations in-between. (F) The frequency spectrum corresponding to the displacement of point 3. Noise has been removed for clarity in the thick red curves of panels (B)–(E), by filtering out frequency components that were beneath the noise floor [see red curve in panel (F) for an example of the noise floor and emerging components]. The theoretical displacement curves (green mid-thickness) were found using the A-scan and vibration results from the fiber and membrane, assuming the fiber was stationary and that the membrane moved as reported [represented by dashed and solid thin black lines, respectively, in panels (B)–(E)].

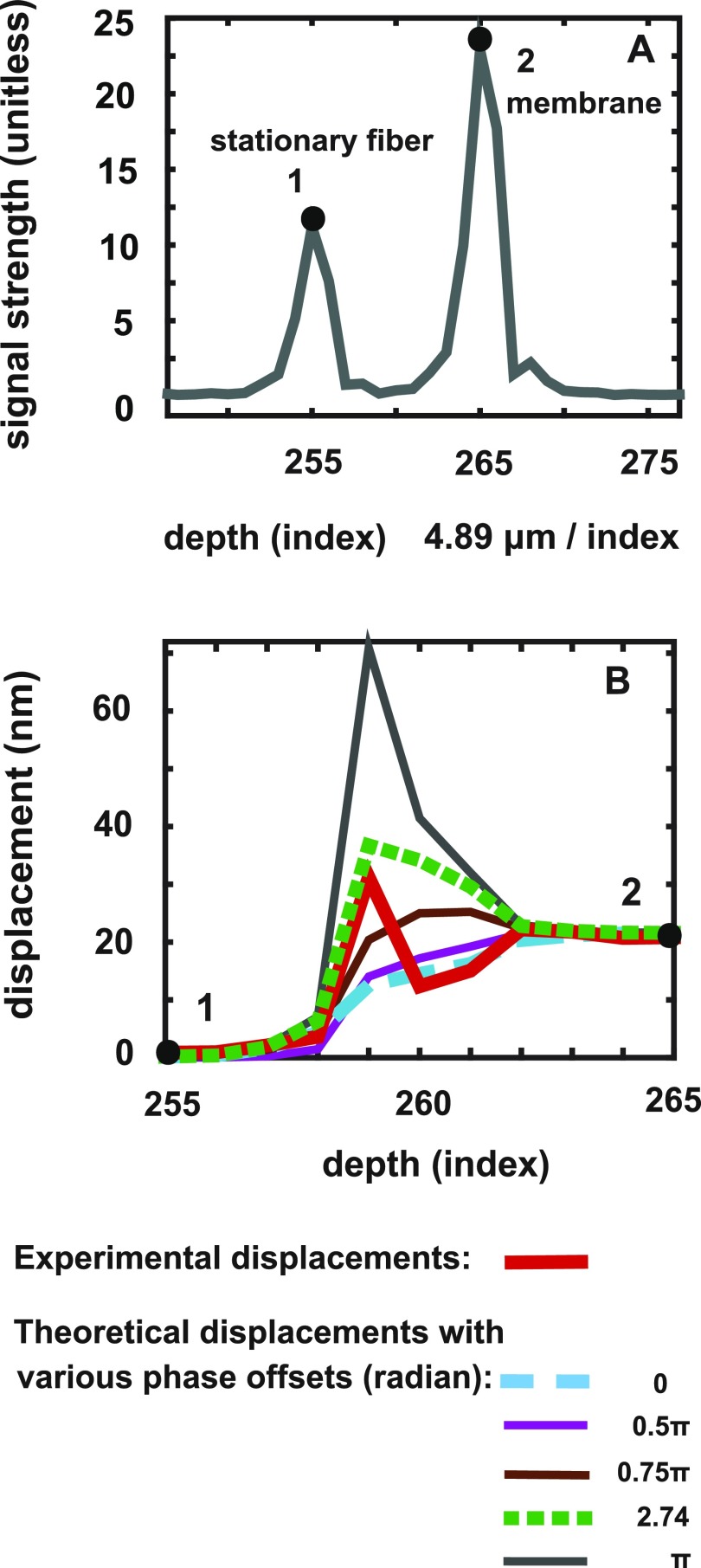
FIG. 4.

(Color online) Responses of the membrane/fiber sample when driven with a 7008 Hz pure tone of a level that resulted in a ∼20 nm vibration of the membrane and no discernible vibration of the fiber. (A) A-scan indicating points 1 and 2 of the stationary fiber and membrane, respectively. (B) Thick red curve: reported response amplitudes at points 1 and 2 and all points in between. (Responses were not distorted, thus waveforms are not shown.) Other curves: theoretical reported displacements when accounting for phase leakage. The calculation used the A-scan and vibration results from the fiber and membrane. Several ΔΘ_AB0 values were used to illustrate the sensitivity of the phase leakage prediction to this value.

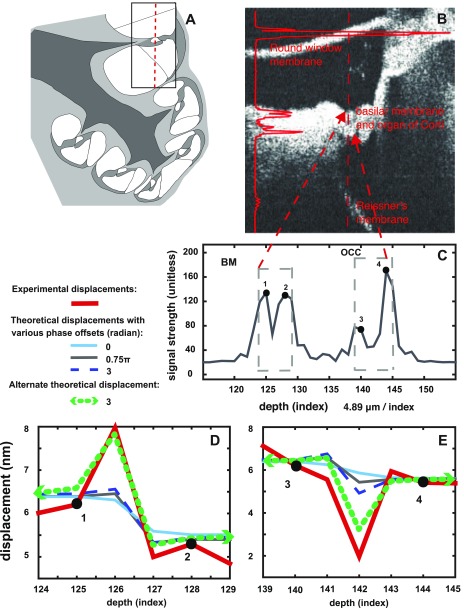
FIG. 5.

(Color online) Cochlear measurements when the ear was driven with a pure tone of frequency 9998 Hz. (A) Sketch of the cochlear region under observation. (B) B-scan, with round window membrane, BM, OCC, and Reissner's membrane surfaces in view. Location of A-scan of vibration measurement is indicated in the red vertical line. The red solid line to the left shows the magnitude of the A-scan, positioned to show the correspondence with structures in the B-scan. (C) A-scan with BM and OCC regions indicated. The regions corresponding to points 1 and 2 (BM region) and points 3 and 4 (OCC regions) are explored in (D) and (E). (D) Thick red curves: reported response amplitudes at points 1 and 2 and in-between and adjacent points. Other curves: theoretical reported displacements when accounting for phase leakage. The calculation used the A-scan and vibration results from the prominent points 1 and 2. Several ΔΘ_AB0 values were used to illustrate the sensitivity of the phase leakage prediction to this value. The thick-dashed green curves show theoretical reported displacement found using a slightly different optical sectioning curve.

B. Comparative background: How heterodyne interferometry measures motion

A brief aside into standard heterodyne interferometry sets the stage for a description of the motion measurement of SDPM (Willemin et al., 1988; Cooper 1999; de La Rochefoucauld et al., 2005). In heterodyne interferometry, a narrowband light source is used, and separated into object and reference beams that have a small offset between their individual frequencies, ω_o and ω_r in radian units. The object beam is focused on a reflector of interest within the tissue, and the reflected object and reference beams are combined at a photodetector. This combined signal contains a component at the difference frequency, ω_c = ω_o – ω_r, termed the carrier frequency. The signal at the carrier frequency can be written as

$$S_{\mathit{H}\mathit{I}}(t)=A_{\mathit{H}\mathit{I}}{e}^{(i({\omega }_{c}t+{\varnothing }_{\mathit{o}\mathit{o}}))},$$ (1)

where ${\varnothing }_{\mathit{o}\mathit{o}}$ is a constant. (The subscript HI indicates “heterodyne interferometry.”) The size of A_HI depends on, among other things, the reflectivity of the object that was focused on. For now, we assume the ideal situation where out-of-focus objects do not reflect significant light, so that there is no signal competition from secondary reflectors. If the object is moving, ω_o is changed by a Doppler shift, $\Delta \omega (t)=2v(t)({\omega }_{\mathrm{o}}/c)$, where $v(t)$ is the velocity of the object. The factor of 2 results because the Doppler shift occurs both on the incident light on and reflected light from the object.

Then,

$$S_{\mathit{H}\mathit{I}}(t)=A_{\mathit{H}\mathit{I}}{e}^{\{i({\omega }_{c}t+(2{\omega }_{\mathrm{o}}/c)\int v(t^{\prime })d{t}^{\prime }+{\varnothing }_{\mathit{o}\mathit{o}})\}}.$$ (2)

Thus,

$$S_{\mathit{H}\mathit{I}}\left(t\right)=A_{\mathit{H}\mathit{I}}{e}^{\left(i\left({\omega }_{c}t+\varnothing \left(t\right)\right)\right)}\hspace{1em}\text{with}\hspace{0.17em}\varnothing \left(t\right)=\frac{2{\omega }_0}{c}{\int }_0^{t}v\left(t^{\prime }\right)d{t}^{\prime }+{\varnothing }_{00}.$$ (3)

Taking the time integral, $\varnothing (t)=(2{\omega }_{\mathrm{o}}/c)\hspace{0.17em}\delta (t)+{\varnothing }_0$, where δ(t) is the displacement of the object and ${\varnothing }_0$ is a constant. Using the relationship ${\omega }_{\mathrm{o}}/c=k_0$, $\varnothing (t)=2k_0\delta (t)+{\varnothing }_0$, and

$$S_{\mathit{H}\mathit{I}}(t)=A_{\mathit{H}\mathit{I}}{e}^{(i({\omega }_{c}t+2k_0\delta (t)+{\varnothing }_0))}.$$ (4)

Displacement is found by analyzing S_HI at the carrier frequency ω_c, and evaluating the phase of the signal $\hspace{0.17em}\varnothing (t)$, resulting in

$$\delta \left(t\right)=\frac{\varnothing \left(t\right)-{\varnothing }_0}{2k_0}=displacement\hspace{0.17em}\hspace{0.17em}found\hspace{0.17em}with\hspace{0.17em}heterodyne\hspace{0.17em}interferometry.$$ (5)

Note, k₀→nk₀ where n is the index of refraction, for measurements that are not in air (n = 1 in air). As will be developed below, the $\hspace{0.17em}{\varnothing }_0$ term has a significant impact when competing signals are present. In practice, the phase of the signal at the carrier frequency ω_c is usually analyzed using an FM demodulator tuned to ω_c and velocity is directly measured rather than displacement.

C. Comparative background: How SDPM measures motion

In SDPM a process similar to that of heterodyne interferometry is used to find motion. SDPM is a functional extension of SDOCT in which the phase of the z-domain signal is used, in addition to the amplitude that was used to form the A-scan.

Using an object at location $Z_0$ to develop an example, the (simplified for brevity) k-domain pattern (termed interferogram) on the photodetector array from this object is

$$S_{\mathit{O}\mathit{C}\mathit{T}}(k)=A_{\mathit{O}\mathit{C}\mathit{T}}(k)e^{ik\{2(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})\}}.$$ (6)

(See, e.g., Izatt and Choma, 2015 for example interferograms.) In general, the path-length difference $(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})$ will not correspond exactly to one of the z-domain indices in the spatial Fourier transform used to go from k to z-space, and this offset will be represented in the phase of the k-domain pattern. Assume $Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}}$ = $Z_p+\delta$, where the position $Z_p$ is perfectly aligned with one of the z-domain indices.

Then,

$$S_{\mathit{O}\mathit{C}\mathit{T}}(k)=A_{\mathit{O}\mathit{C}\mathit{T}}(k)e^{i\{2k{Z}_p+{[2k\delta ]}_0\}}.$$ (7)

${[2k\delta ]}_0\hspace{0.17em}$ is a phase “constant”—it is not a function of k and can be written and thought of as $2k_0\delta$, where $k_0$ is the center wavenumber of the light source and δ is a sub-index distance offset. We are interested in motion, so we write δ = δ₀ + δ(t) and

$$S_{\mathit{O}\mathit{C}\mathit{T}}(k)=A_{\mathit{O}\mathit{C}\mathit{T}}(k)e^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})+\Theta (\mathrm{t})\}},$$ (8)

where

$$\Theta (t)=2k_0{\delta }_0+2k_0\delta (t)={\Theta }_0+2k_0\delta (t).$$

Thus, by looking at the phase in the z-domain Fourier transform of the interferogram, the displacement can be found,

$$\delta \left(t\right)=\frac{\Theta \left(t\right)-{\Theta }_0}{2k_0}=displacement\hspace{0.17em}found\hspace{0.17em}with\hspace{0.17em}SDPM.$$ (9)

As noted above, k₀→nk₀, where n is the index of refraction, for measurements that are not in air.

The similarity between Eqs. (5) and (9) is clear. Just as with heterodyne interferometry, SDPM provides a phase-based method to find displacement. The processing steps are as follows: First we take the spatial Fourier transform of S(k) to cast the signal into the z domain, the A-scan. In order to measure motion, we take a series of A-scans at a fixed lateral position at a rapid sampling rate; the resulting data set is termed an M-scan. We use the magnitude of the A-scan to find the z locations of peaks, indicating reflective structures. We can then find the motion of these reflective structures by evaluating the phase of the M-scan, $\Theta (t)$, at the z indices corresponding to the A-scan peaks. Ideally, one can find the displacement of all the locations in the A-scan simultaneously. However, as developed below, “phase leakage” due to signal competition can lead to erroneous results when measuring motion at z locations in which the A-scan magnitudes are relatively small. As with the case for heterodyne interferometry, the ${\Theta }_0$ term looks like a meaningless offset, but can become important in the case of competing signals. We discuss competing signals next.

D. Competing signals, heterodyne interferometry

In heterodyne interferometry, one focuses the laser on the object of interest, and hopes that the light returning to combine with the reference beam, which forms the signal for displacement analysis, comes only from the in-focus object. However, if there is another illuminated object that is reflective enough, it will compete with the signal from the in-focus object. Call the signal from the in-focus object “A_HI” and the signal from the out-of-focus object “B_HI.” The size of competing signal B_HI depends on how reflective object B is and the focusing strength of the system—its optical sectioning capability. In heterodyne interferometry, the optical sectioning is determined predominately by the numerical aperture of the system's objective lens. For example, the full-width-half-maximum (FWHM) of a lens with NA of 0.25 is ∼14 μm, with broad skirts. The skirts can be steepened with confocal, light-blocking techniques (de La Rochefoucauld et al., 2005; Ren and Nuttall, 2001; Dalhoff et al., 2001).

To continue with the analysis, when there are two signals, with magnitudes A_HI and B_HI, they sum,

$$A_{\mathit{H}\mathit{I}}{e}^{i({\omega }_{c}t+{\varnothing }_A(t))}+B_{\mathit{H}\mathit{I}}{e}^{i({\omega }_{c}t+{\varnothing }_B(t))}=e^{i{\omega }_{c}t}(A_{\mathit{H}\mathit{I}}{e}^{i{\varnothing }_A(t)}+B_{\mathit{H}\mathit{I}}{e}^{i{\varnothing }_B(t)}).$$ (10)

From Eq. (5), the A and B phases are related to the motion of objects A and B as

$${\varnothing }_A(t)=2k_0{\delta }_A(t)+{\varnothing }_{A0}\hspace{0.17em}\text{and}\hspace{0.17em}{\varnothing }_B(t)=2k_0{\delta }_B(t)+{\varnothing }_{B0}.$$ (11)

The common $e^{i{\omega }_{c}t}$ term representing the carrier frequency is factored out, and the phase of the summed signal, which is used to find the reported displacement, is found by writing the bracketed terms in real and imaginary terms

$$A_{\mathit{H}\mathit{I}}{e}^{(i{\varnothing }_A(t))}=A_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\hspace{0.17em}({\varnothing }_A(t))+i{A}_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\hspace{0.17em}({\varnothing }_A(t)),$$

$$B_{\mathit{H}\mathit{I}}{e}^{(i{\varnothing }_B(t))}=B_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\hspace{0.17em}({\varnothing }_B(t))+i{B}_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\hspace{0.17em}({\varnothing }_B(t)).$$

Thus

$$\begin{array}{c}{A}_{\mathit{H}\mathit{I}}{e}^{(i{\varnothing }_A(t))}+B_{\mathit{H}\mathit{I}}{e}^{(i{\varnothing }_B(t))}=A_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\hspace{0.17em}({\varnothing }_A(t))+B_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\hspace{0.17em}({\varnothing }_B(t))+i\{A_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\hspace{0.17em}({\varnothing }_A(t))+B_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\hspace{0.17em}({\varnothing }_B(t))\}.\end{array}$$ (12)

From this we can find the phase, which will be used to report the displacement of the in-focus object via Eq. (5). Note that signal B_HI is competing with (contaminating) the signal A_HI (from the in-focus object) in the determination of the motion of the in-focus object.

Signal-competition, heterodyne interferometry

$$={\varnothing }_T\left(t\right)=\arctan \left\{\frac{A_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\left({\varnothing }_A\left(t\right)\right)+B_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{sin}\left({\varnothing }_B\left(t\right)\right)}{A_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\left({\varnothing }_A\left(t\right)\right)+B_{\mathit{H}\mathit{I}}\hspace{0.17em}\text{cos}\left({\varnothing }_B\left(t\right)\right)}\right\},$$ (13a)

where $\hspace{0.17em}{\varnothing }_A(t)=2k_0{\delta }_A(t)+{\varnothing }_{A0}$ and ${\varnothing }_B(t)=2k_0{\delta }_B(t)+{\varnothing }_{B0}$.

To gain understanding of Eq. (13a), we will initially neglect the constant phases ${\varnothing }_{A0}$ and ${\varnothing }_{B0}$ and come back to them later. Consider the size of the 2k₀δ(t) terms. In the cochlea, δ(t) is almost always less than 100 nm, and for moderate sound levels is less than ∼20 nm. k₀ in the case of a HeNe laser is $2\pi /630\hspace{0.17em}\hspace{0.17em}\text{nm}$, and using 20 nm for the amplitude of δ(t), $2k_0\delta (t)=4\pi (20\hspace{0.17em}\hspace{0.17em}\text{nm})/630\hspace{0.17em}\hspace{0.17em}\text{nm}=0.4\hspace{0.17em}$ radian. This value is small enough that small angle approximations can often be used and offer insight.

Then,

$${\varnothing }_T\left(t\right)\approx \frac{A_{\mathit{H}\mathit{I}}{\varnothing }_A\left(t\right)+B_{\mathit{H}\mathit{I}}{\varnothing }_B\left(t\right)}{A_{\mathit{H}\mathit{I}}+B_{\mathit{H}\mathit{I}}}.$$ (13b)

Thus, the reported phase [leading directly to reported displacement via Eq. (5)] would be a weighted average of the phase corresponding to each of the two competing signals, with the weighting equal to the signal strengths A_HI and B_HI. However, the presence of the phase constants ${\varnothing }_{A0}$ and ${\varnothing }_{B0}$, which are not generally small, makes this simple scheme incorrect. de La Rochefoucauld et al. (2005) showed that due to these phase constant terms, ${\varnothing }_T(t)$ can even be larger or smaller than both of the individual phases, ${\varnothing }_A(t)\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\varnothing }_B(t)$. Nevertheless, the weighted average notion is an intuitively clear reference point for prediction.

E. Competing signals, SDPM

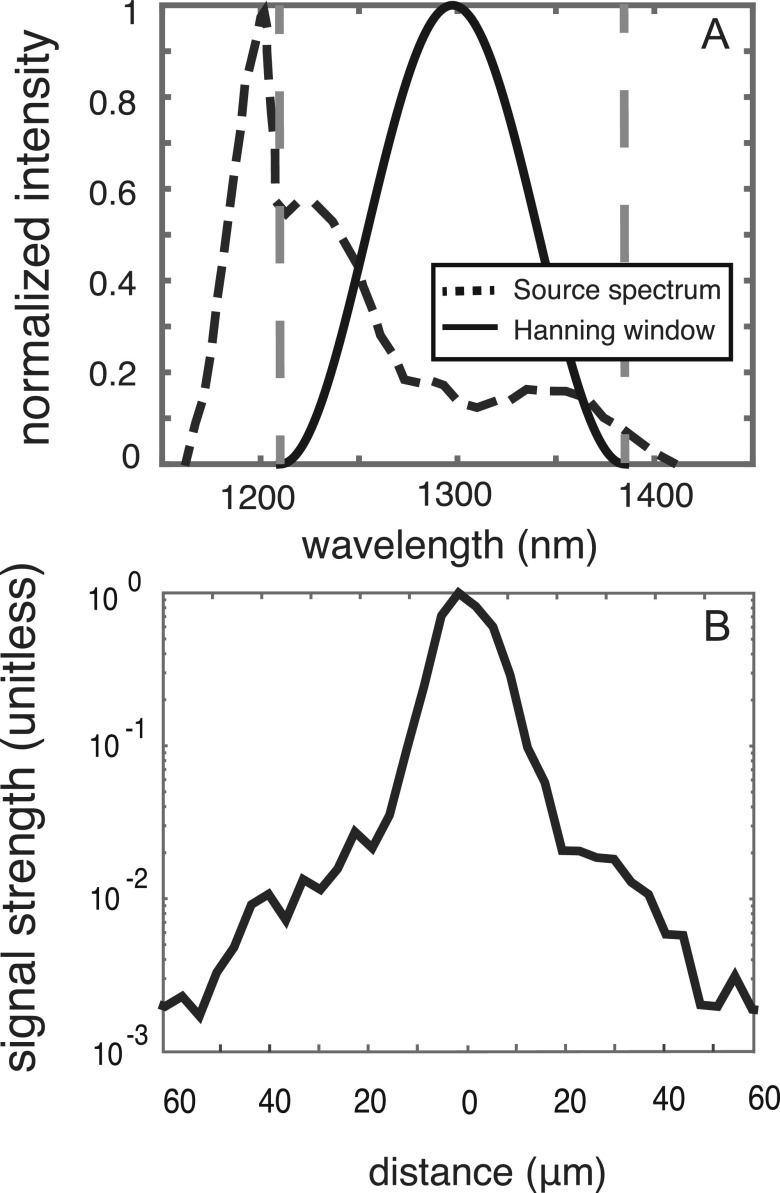
Heterodyne interferometry focuses at one depth and light returning from other depths is unwanted competition. In contrast, with SDPM, the focus is deliberately broad so that light is collected simultaneously from several mm in the direction along the axial beam. In this case the optical sectioning is determined, not by the focusing of the lens, but by the point spread function of the light source, derived from its optical spectrum (Izatt and Choma, 2015). The width of the point spread function is inversely proportional to the bandwidth of the light source. The spectrum of the Telesto's light-source, measured with a Hewlett Packard 70952B Optical Spectrum Analyzer, is shown in Fig. 1(A) as a black dashed line. The region inside the vertical gray dashed lines shows the wavelength range that is actually used by the Telesto, based on our measurements with the reference beam alone. The solid black curve is a Hanning curve that is an ideal light-source spectrum. To more closely attain that ideal spectral shape for the SDOCT analysis, the output of the photodetector array (the raw data) is multiplying by the ratio of the Hanning curve to the actual light source spectrum (Tripathi et al., 2002). The system's optical sectioning curve can be determined experimentally, by imaging a mirror (finding the A-scan magnitude) with the OCT system. Using a mirror's image to experimentally determine the optical sectioning curve has been used for both OCT and heterodyne systems (e.g., Tripathi et al., 2002; Cooper, 1999; de La Rochefoucauld et al., 2005). The optical sectioning curve we measured for the Telesto is in Fig. 1(B). The FWHM is ∼12 μm, with quite steep skirts. Still, a strong reflector's signal can “leak” into the signal of other axial locations.

FIG. 1.

Optical sectioning of the Thorlabs Telesto. (A) The black dashed line shows the measured spectrum of the light source and the vertical gray dashed lines show the approximate spectral range used by the Telesto, with the black line showing a Hanning curve used for spectral correction. (B) The resulting optical sectioning curve of the Telesto, found by taking the A-scan image of a mirror.

The analysis of signal competition in SDPM, termed “phase leakage,” proceeds as for heterodyne interferometry: Imagine we want to find the motion of the point at $Z_0$. The object at or closest to $Z_0$ contributes signal $A_{OCT\_\_Z_0}$ and ideally this is the only signal contributing to the analytical index at $Z_0$. However, imagine that there is another object B, which is not at $Z_0$ (for example, 10 μm deeper or shallower axially). This object will also contribute to the index at $Z_0$. Call $A_{OCT\_Z_0}$ and $B_{OCT\_Z_0}$ the two signal strengths at the index corresponding to $Z_0$. For simplicity, assume A and B are the only two reflectors in the axial line. Then the total signal corresponding to the index at $Z_0$ is

$$\begin{array}{c}{A}_{OCT\_Z_0}{e}^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})+{\Theta }_A\}}+B_{OCT\_Z_0}{e}^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})+{\Theta }_B\}}\\ =e^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})\}}[A_{OCT\_Z_0}{e}^{i{\Theta }_A}+B_{OCT\_Z_0}{e}^{i{\Theta }_B}].\end{array}$$ (14)

The exponential term out front, $e^{i\left\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})\right\}}$, just identifies the location of the reflector at $Z_0$. The bracketed part to the right is used to find the phase of the signal at index $Z_0$, which will be used to find displacement as in Eq. (9). Just as in heterodyne interferometry, the phase of the summed signal can be found by writing the bracketed terms as real and imaginary parts and from this to find the total phase.

Signal-competition, SPDM,

$${\Theta }_T\left(t\right)=\text{arctan}\left\{\frac{A_{OCT\_Z_0}\hspace{0.17em}\text{sin}\left({\Theta }_A\right)+B_{OCT\_Z_0}\hspace{0.17em}\text{sin}\left({\Theta }_B\right)}{A_{OCT\_Z_0}\hspace{0.17em}\text{cos}\left({\Theta }_A\right)+B_{OCT\_Z_0}\hspace{0.17em}\text{cos}\left({\Theta }_B\right)}\right\},$$ (15)

where, from Eq. (9),

$${\Theta }_A=2k_0{\delta }_A(t)+{\Theta }_{A0}\hspace{1em}\text{and}\hspace{0.17em}{\Theta }_B=2k_0{\delta }_B(t)+{\Theta }_{B0}.$$ (16)

The similarity between Eqs. (13a) and (15) is clear. As with heterodyne interferometry, the motions δ(t) are often small enough that, if it were not for the ${\Theta }_{A0}$ and ${\Theta }_{B0}$ terms, the 2k₀δ(t) terms would allow for small angle approximations to apply. This would make the total phase, ${\Theta }_T$, equal to a weighted average of the phases of the summing signals, with the weighting corresponding to the signal strength of each structure in the image, when evaluated at the index of interest. As in heterodyne interferometry, this weighted average approximation is spoiled by the presence of the ${\Theta }_{A0}$ and ${\Theta }_{B0}$ terms, which are not generally small. In SDPM there are as many potential competing signals as there are z indices in the A-scan, N. Thus, we have a sum over N, which is a simple generalization of our two-reflector example. Such a sum over N was in Ellerbee and Izatt (2007). In practice, significant phase leakage usually involves signals from locations with bright reflectors (local maxima in the A-scans) contaminating signals from near-by locations. How close they must be for contamination to occur depends on their relative reflectivity, the signal strength fall-off [found from the optical sectioning curve, e.g., Fig. 1(B)] and the relative size of the displacements. In the discussion section we graph and explore examples.

III. METHODS

Displacement measurements were made with a Thorlabs Telesto I SDOCT, operating at sampling rate of 92 kHz. For the experiments presented here, the photodetector raw data had been preprocessed by the Thorlabs software: the background had been subtracted and curve shaping of the optical spectrum had been applied.

A signal generator (Wavetek) and audio amplifier (Tucker Davis Technologies HB7) and speaker (Fostex FT17H) were used to deliver tones at moderate sound pressure levels. Two types of preparation were used to demonstrate and explore signal competition.

• (1)A test sample composed of two simple reflectors (Fig. 2). A transparent polymer membrane terminating a ∼2 mm diameter glass tube formed one reflector, and a flatly terminated glass fiber 125 μm in diameter, positioned ∼55 μm behind the membrane formed the second. The membrane was created by plunging the glass tube into a beaker of water that had a ∼1 μm thick layer of UV-cured optical adhesive (Norland Products, Cranbury, NJ) floating on its surface. The glass fiber was then threaded into the tube with a micromanipulator (Marzhauser, Germany) to a position with its flat end close to the membrane, and adhered to the tube at the far end. Acoustic tones were delivered open-field to the sample.
• (2)Post-mortem adult Mongolian gerbil (Meriones unguiculatus) cochleae. The gerbils had been euthanized before the experiment. The bulla was opened with blunt forceps to expose the basal cochlea. The head was attached to an angle-varying stage so that the OCT beam could be directed through the round window membrane and the basilar and tectorial membranes could be imaged by the SDOCT system. Acoustic tones were delivered to the ear canal via a tube connected to the speaker.

IV. RESULTS

A. Phase leakage demonstration on fiber/membrane sample

The inset in Fig. 2(A) shows a sketch of the fiber/membrane test sample and its A-scan and Fig. 2(B) is a photograph of the test system, showing the optical fiber end close to the membrane. Figures 3 and 4 show vibration results and theoretical predictions for the test sample. The division between the “high modulation” and “low modulation” cases discussed in de La Rochefoucauld et al. (2005) is at a displacement of ∼1/10λ, corresponding to ∼130 nm. In Fig. 3 the membrane's displacement was 200 nm and the consequences of phase-leakage included substantial distortion, as expected for this “high modulation” case. In Fig. 4 the membrane's motion was small enough that “low modulation” behavior was observed and phase leakage did not cause detectable distortion.

The A-scan in Fig. 3(A) contained two prominent peaks (index 367 = point 1 and index 377 = point 4), corresponding to the fiber tip and membrane, separated by nine z-indices (11 indices total), a distance of ∼55 μm. We were interested in the vibration waveforms reported by the SDOCT system at the z locations corresponding to indices of the peaks and the indices in between the peaks. The reported vibration waveform at each index was found using the phase of the z-domain response at each of the indices as in Eq. (9). This time-domain waveform was cast into the frequency domain, and the amplitudes and phases at the stimulus frequency and harmonics that emerged from the noise were used to create clean time-domain vibration waveforms, in which noise in the waveform had been eliminated. The time domain displacement responses reported at locations 1–4 in the A-scan are shown in the thick red curves in panels (B)–(F). The thick red curves shown at points 2 and 3 (indices 369 and 370) between the membrane and fiber were distorted sinusoids. The reported displacement at point 1 (the fiber) was also a distorted sinusoid. The distortion was not generated by the sound source, which was confirmed by the observation that the reported displacement of the membrane [point 4 shown in panel (E)] did not contain harmonic components above the ∼4 nm noise floor.

Between the membrane and the fiber is a void and the displacement responses reported at locations 2 and 3 were due to phase leakage from the signals of the membrane and fiber. To use the theory developed above to find the expected phase leakage and then the predictions for reported displacement, we assumed that the fiber (point 1) was stationary [dashed black lines at zero displacement in panels (B)–(E), but hidden in (B)] and that the membrane (point 4) was moving with the reported displacement shown in the thick red curve of panel (E): a pure sinusoid with amplitude of 205 nm [thin black line in panels (B)–(E), but hidden in (E)]. These dashed and solid thin black curves are included in all of the panels as a reference. Location 1, the fiber, was expected to be stationary and we did not know if the reported non-zero response [thick red curve in panel (B)] was due to signal competition from the membrane, or actual motion at the fiber. Thus, as noted above, for the theoretical analysis we set the motion at location 1 to zero. Setting it to a small non-zero value did not alter the theoretical predictions.

To summarize: for the theoretical prediction of the reported motion, we assumed that structures were only present at the A-scan peaks corresponding to the fiber and membrane (indices 367 and 377). We computed the theoretical reported displacements, at indices corresponding to points 1, 2, 3, and 4 by evaluating Eq. (15) at each of these indices [mid-thickness green curves in Figs. 3(B)–3(E)]. The coefficients, $A_{OCT\_Z_0}$ and $\hspace{0.17em}{B}_{OCT\_Z_0},$ in Eq. (15) were determined using the signal strength at the peaks corresponding to the fiber (index 367) and membrane (index 377) from the A-scan shown in Fig. 3(A), multiplied by the appropriate value from the optical sectioning curve of Fig. 1(B), given the distance between the peak index and the index of interest. Important free parameters were the phase constants, ${\Theta }_{A0}$ and ${\Theta }_{B0}$ in Eq. (15). When only two signals contribute to the sum (as we are assuming), only their difference, $\Delta {\Theta }_{AB0}$, is important. We used $\Delta {\Theta }_{AB0}$ = 1.35 radian to generate the theoretical predictions in Fig. 3. Also, we recognized that for the broadband SDOCT light source, the “$k_0$” value in Eq. (15) is actually a spread of k values; therefore, we calculated Eq. (15) not only with a central wavenumber of the light source called “single k,” but also with a sum of sines and cosines in the numerator and denominator over a range of k values representing the bandwidth of the light-source. The spread in k calculations usually did not affect the results substantially; therefore, we only show the single k results.

The theoretical predictions based on phase leakage are similar to the reported displacements for the locations between the membrane and fiber where, in fact, nothing was present, and is a clear demonstration of the presence of predictable phase-leakage-based signal competition in SDPM measurements. The harmonic distortion observed is produced by signal competition when the displacements are ≳1/10 the size of the wavelength of the light source, which is the “high modulation” case described in de La Rochefoucauld et al. (2005).

Figure 4 shows results from the same sample as Fig. 3, stimulated at a lower sound pressure level to demonstrate the “low modulation” case, with the membrane displacement amplitude at 19 nm. The reported vibration waveforms at indices between those of the prominent reflectors were not distorted: they did not contain harmonics above the noise floor. We show the amplitude of the responses reported at the indices of the two peaks (point 1 at index 255 → fiber end, and point 2 at index 265 → membrane) and all the nine indices in between [Fig. 4(B)]. The experimentally reported displacements are presented in the thick red line. The three indices closest to point 1 (256–258) report displacements that are relatively low and similar to that of point 1 but are non-zero. The three indices (262–264) closest to the membrane at point 2 report displacement amplitudes similar to point 2's value of 19 nm. However, indices 259–261 show a range of reported displacement amplitudes that in one case, index 259, was substantially larger than that of point 2.

The non-bold-red curves in Fig. 4(B) are theoretical predictions using Eq. (15) and following the same procedure as described above when generating the phase-leakage predictions for Fig. 3. That is, we assumed that the only structures actually present were at points 1 and 2 and used the A-scan values for these points from Fig. 4(A) and the optical sectioning curve of Fig. 1(B) to find the coefficients for entering into Eq. (15). Predictions were found with $\Delta {\Theta }_{AB0}$ varying through a range of values. When $\Delta {\Theta }_{AB0}$ was zero (long-dashed light blue curve) the displacement values between the two reflectors take on the weighted average behavior we described when a small angle approximation was applied to Eq. (15). The theoretical prediction was closest to the experimental result when $\Delta {\Theta }_{AB0}$ = 2.74 radian [short-dashed green curve in panel (B)]. Phase leakage can clearly account for an anomalously large displacement reported at a location that contains comparable signal from two different locations.

B. Phase leakage demonstration on a cochlear sample

Organ of Corti responses due to ear canal stimulation with a 10 kHz pure tone are shown in Fig. 5. The cochlear B-scan image in Fig. 5(B) was reduced to the single vertical line indicated in the red dashed line, to give the A-scan in Fig. 5(C). The A-scan can be considered to be comprised of two important regions: a BM region with prominent peaks 1 and 2 (indices 125 and 128) and an OCC region with prominent peaks 3 and 4 (indices 140 and 144). Experimentally reported displacement amplitudes for those two regions are shown separately in the thick red curves in panels (D) and (E).

In (D), BM region points 1 and 2 reported displacement amplitudes quite similar to each other, slightly greater than 6 and 5 nm, respectively. The point adjacent to 1 (index 125) at index 124 reported a similar displacement amplitude as point 1, and the two points adjacent to 2 (index 128) at 127 and 129 reported displacement amplitudes similar to point 2. The intermediate point at index 126 reported a substantially larger amplitude, 8 nm.

In E, the OCC region, point 3 (index 140) had a reported displacement amplitude of ∼6.2 nm and point 4 (index 144) of ∼5.5 nm. The locations in between these have reported displacement amplitudes similar to those values except index 142, which reported a displacement less than 2 nm.

For the theoretical comparison, the phase leakage prediction was computed as for Figs. 3 and 4, using Eq. (15) and assuming that the only structures were those of the two prominent peaks (points 1 and 2 for the BM region and points 3 and 4 for the OCC region). In reality, the cochlear sample is different from the simple fiber/membrane test sample in that there are structures in between those of the prominent peaks; thus, the phase leakage calculation is only a portrayal of the degree of phase leakage possible.

In Fig. 5(D) the predictions for reported displacements at locations in the BM region are shown in the non-red-bold curves, with $\Delta {\Theta }_{AB0}$ varied through a range of values. In Fig. 5(E) the same is done for the OCC region. The theoretical displacement amplitudes at locations between the prominent reflectors changed as $\Delta {\Theta }_{AB0}$ was varied. The theoretical predictions closest to the experimental result for both regions had $\Delta {\Theta }_{AB0}$ set to 3 radian [long-dashed blue curves in Figs. 5(D) and 5(E)]. Predictions that more closely matched the anomalously large (index 126) and small (index 142) experimental displacement results could be produced by changing the relative contributions of the two reflectors by less than a factor of 2. This could arise with a realistically small discrepancy in the position or steep fall off of the optical sectioning curve [Fig. 1(B)], and reinforces one of the central messages of this report: that locations that are local minima in the A-scan are particularly vulnerable to phase leakage artifacts. Local minima indices 126 and 142 had the most extreme variation in the theoretically reported displacement amplitudes. However, the reported displacements of even the local maxima points 1 and 2 were affected slightly by phase leakage, in that the predicted displacement values varied by ∼5% as the $\Delta {\Theta }_{AB0}$ parameter was changed.

V. DISCUSSION

One objective of this report was to describe the basic similarity between SDPM and heterodyne interferometry, which is useful for auditory physiologists who are familiar with the latter. The second objective was to explore the manifestation of the phase-leakage artifact of the SDPM technique in displacement responses of the cochlea, and demonstrate the core similarity between phase leakage and the signal competition problem of heterodyne interferometry (de La Rochefoucauld et al., 2005). The qualitative agreement between experimental and theoretical reported displacements from the simple test system shown in Figs. 3 and 4 reassures that the theoretical description of phase leakage is appropriate.

The phase-leakage problem in SDPM was first described by Ellerbee and Izatt (2007), who discovered the problem when studying the motion of cardiomyocytes on a coverslip. The relatively bright reflection of the coverslip caused its signal to leak into the locations of the cells, 40 μm away, altering the reported motion of the cells. They demonstrated post-processing methods for correction, in which the static coverslip signal was measured separately and subtracted. This strategy is not available for cochlear mechanics, because the competing reflectors cannot be isolated and characterized separately.

Because of the steep optical sectioning of SDOCT, phase leakage is manageable for cochlear measurements as long as reasonable precautions are taken. As the results above showed, local minima are the most at-risk for phase-leakage artifacts, because they can have nearly equal contributions of signal from adjacent local maxima. In addition to signal strength, the displacement magnitude from a competing signal is also important in determining the degree of leakage, which is intuitively clear in the weighted-sum approximation.

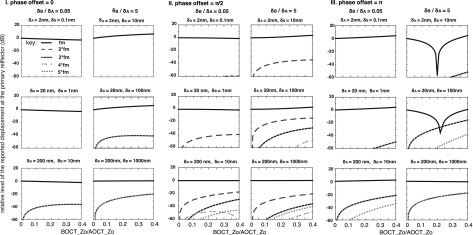
In order to generalize phase leakage results graphically, in Fig. 6 we show predictions of the error in the displacement reported at a location A, due to signal leakage from a location B. Following from what has been learned, for this section we assume that displacement is only being measured at local maxima. Figure 6 would be applied to estimate the effect of the signal from one A-scan local maxima (at B) to the measured displacement at a nearby A-scan local maxima (at A). The true displacements are taken to be pure sinusoids with different amplitudes. For this illustration, we use displacement amplitude ratios of 5 (where structure B vibrates with a larger amplitude than A) and 0.05 (where structure A moves more than B). The x axis is the ratio of the signal from B (the contaminating signal) to the signal from A: the ratio of the coefficient $\hspace{0.17em}{B}_{OCT\_Z_0}$ to $A_{OCT\_Z_0}$ in Eq. (15). The y axis shows the difference of the reported displacement at A, relative to the true displacement at A. To make this clear with two examples: a value of 0 dB in the fundamental (solid-line) curve signifies a reported displacement at the fundamental frequency that is equal to the actual displacement at the fundamental frequency—so no error, whereas a value of 4 dB in this curve signifies a reported displacement at the fundamental frequency 4 dB greater than the actual displacement at the fundamental. As the second example, a value of −40 dB in a harmonic curve corresponds to a reported displacement at the harmonic frequency that is 40 dB less than actual displacement at the fundamental frequency. The harmonic curves show the appearance of these components, which would not be present without phase leakage. In order to make use of these graphs, one must first determine the optical sectioning curve of the OCT system in use, by taking the A-scan of a mirror to generate an optical sectioning curve like that of Fig. 1(B). With this curve and an A-scan of the sample, one can estimate the strength of a signal from one location (B) that has leaked to the location (A) of interest.

FIG. 6.

Effect of phase leakage as a function of several parameters. The x axis in all the figures is the ratio of the signal from B (the contaminating signal) to the signal from A at the location Z₀, where A is located. The y-axis presents the difference between the reported vibration displacement amplitude and the actual displacement at location A, due to phase leakage from location B. The actual displacement amplitude of A and B is noted at the top of each panel. The ratio of B to A displacement is the same for each column, and noted at the top. For this figure we show ratios of 5 and 0.05 in sets of two columns; another case, for which the displacements are similar, is treated in the discussion text. Three different phase offsets are analyzed, 0, π/2, and π, as noted at the top of each set of two columns. These were chosen because values close to π typically give the most extreme variations in amplitude and the value of π/2 introduces more harmonics into the reported waveform.

It is apparent from the graphs in Fig. 6 that for relatively large displacements (more than ∼1/10th of the light source wavelength, ∼100 nm for our system), significant harmonics can be erroneously reported even for quite small signal strength ratios (most apparent in third row of panels). If the x axis were extended to signal strength ratios close to 1 (situation that can occur at local minima in the A-scan), larger and more numerous harmonics would develop, such as were apparent in the experimental data of Fig. 3 (and see de La Rochefoucauld et al., 2005). These large, numerous harmonics emerge when the sizes of the two competing signals are nearly equal, which apparently occurred in our experiments at a measurement location between two bright reflectors.

A reassuring message from Fig. 6 is that for signal strength ratios below 0.1, and motions less than 100 nm, the effect of signal competition is reasonably small. From Fig. 1(B), at a distance of ∼10 μm the optical sectioning curve is down to a value of 0.1. Thus, experimentally measured displacements from local maxima are predicted to be correct to a within a few percent, and to not be distorted.

In SDOCT measurements, displacement can be calculated at every location in the A-scan and often a structure will span more than one axial index. In our system, the axial indices were separated by ∼5 μm, and at that distance the optical sectioning curve [Fig. 1(B)] is down to a value of ∼0.5. Thus, a question that is particularly relevant to SDOCT measurements, is what effect will signal from neighboring points that are moving with the same vibration have on each other? The answer that emerges from the theory is reassuring. Going back Eq. (14), the total signal corresponding to the index at $Z_0$, due to signals A and B was $e^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})\}}[A_{OCT\_Z_0}{e}^{i{\Theta }_A}+B_{OCT\_Z_0}{e}^{i{\Theta }_B}]$, where ${\Theta }_A=2k_0{\delta }_A(t)+{\Theta }_{A0}$ and ${\Theta }_B=2k_0{\delta }_B(t)+{\Theta }_{B0}$. In the special case we are investigating here, ${\delta }_A(t)={\delta }_B(t)$, so the term proportional to ${\delta }_A(t)$ can be factored out and the total signal becomes $e^{i\{2k(Z_0-Z_{\mathit{r}\mathit{e}\mathit{f}})\}}{e}^{i\{2k_0{\delta }_A(t)\}}[A_{OCT\_Z_0}{e}^{i{\Theta }_{A0}}+B_{OCT\_Z_0}{e}^{i{\Theta }_{B0}}]$. The bracketed term with the problematic phase-offset terms is not time dependent, and the phase corresponding to this term will only give rise to a DC offset to the reported displacement. Thus, the interesting time-dependent variations in displacement will be reported accurately from the time dependent part of the phase, $2k_0{\delta }_A(t)$.

In most of the previous measurements of intracochlear motion using SDPM, local maxima in the A-scans have been the points at which displacement was reported. This choice was largely made because the local maxima were identified with cochlear structures, and thus of intrinsic interest. Fortunately, this choice also avoided significant phase leakage artifacts. Moreover, a recent article explicitly stated that displacement measurements were made at local A-scan maxima in order to avoid phase-leakage artifacts (Lee et al., 2016). Earlier heterodyne-OCT vibration measurements explored signal discrimination: Hong and Freeman (2006) showed that the motion of two surfaces, one stationary and the other vibrating at an amplitude of ∼17 nm, could be discriminated as long as their separation was at least 10 μm. For smaller separations, the stationary object was reported to vibrate and the vibrating object was reported to move with an even larger vibration, ∼21 nm. Thus, phase leakage artifacts appeared in this early heterodyne-OCT vibration study.

In conclusion, the issue of signal discrimination has been a concern of optical vibration measurements in the cochlea for decades. In this study, we showed that the core analysis of the signal competition problem in SDOCT is the same as that in heterodyne interferometry. We demonstrated the ability of this analysis to predict experimental results, including substantial harmonic distortion and anomalously large and small displacements reported at locations between bright reflectors. The core similarity between SDOCT and heterodyne interferometry allows for the transfer of understanding of signal competition from heterodyne interferometry to the next generation of optical measurements in the cochlea.