Density overwrites of Internal Tumor Volumes in Intensity Modulated Proton Therapy plans for mobile lung tumors

Abstract

The purpose of this study was to investigate Internal Tumor Volume (ITV) density overwrite strategies to minimize Intensity Modulated Proton Therapy (IMPT) plan degradation of mobile lung tumors.

Four planning paradigms were compared for nine lung cancer patients. IGTV and ICTV structures were defined encompassing their respective volumes in every 4DCT phase. The paradigms use different planning CT (pCT) created from the Average Intensity Projection (AIP) of the 4DCT, overwriting the density within the IGTV to account for movement. The density overwrites were: a) constant filling with 100 HU (C100) or b) 50 HU (C50), c) Maximum Intensity Projection (MIP) across phases, and d) Water Equivalent Path Length (WEPL) consideration from beam’s-eye-view. Plans were created optimizing dose-influence matrices calculated with fast GPU Monte Carlo (MC) simulations in each pCT. Plans were evaluated with MC on the 4DCTs using a model of the beam delivery time structure. Dose accumulation was performed using deformable image registration. Interplay effect was addressed applying 10 times rescanning.

Significantly less DVH metrics degradation occurred when using MIP and WEPL approaches. Target coverage (D99 ≥ 70 Gy(RBE)) was fulfilled in most cases with MIP and WEPL (D99_WEPL = 69.2 ± 4.0 Gy(RBE)), keeping dose heterogeneity low (D5 − D95_WEPL = 3.9 ± 2.0 Gy(RBE)). The mean lung dose was kept lowest by the WEPL strategy, as well as the maximum dose to organs at risk (OARs). The impact on dose levels in the heart, spinal cord and esophagus were patient specific.

Overall, the WEPL strategy gives the best performance and should be preferred when using a 3D static geometry for lung cancer IMPT treatment planning. Newly available fast MC methods using make it possible to handle long simulations based on 4D data sets to perform studies with high accuracy and efficiency, even prior to individual treatment planning.

1. Introduction

Radiation therapy is the mainstay of treatment for inoperable non-small-cell lung cancer (NSCLC). However, NSCLC tumors usually show significant respiratory motion, to which particle therapy is especially sensitive due to the resulting range variations (Knopf and Lomax, 2013). Additionally, the tumor often moves in an orthogonal direction from beam’s-eye-view, which may exacerbate the effect. There are techniques to reduce the dosimetric effects of motion during delivery of a certain plan. Gated therapy can be employed to deliver the plan only when the tumor is within a predefined region; rescanning of IMPT can be employed to give a more homogeneous dose by reducing the interplay effect between the pencil beam scanning delivery pattern of the IMPT plan and the tumor movement; or even delivering the treatment without limitations with the free breathing technique. Regardless of the delivery approach, the tumor motion must be taken into account during the planning stage. It is common practice to define an internal tumor volume (ITV) extracted from a 4-dimensional CT (4DCT), representing the patient geometry and the variations the field would encounter during delivery. By planning in such contour, the plan is more robust towards dosimetric effects caused by geometry changes.

Protons have the potential to offer a dosimetric advantage over photons because they stop within the patient releasing most of their energy at a certain position. This adds an extra degree of freedom for treatment optimization (Lomax, 1999; Lomax et al., 2004) but also introduces additional uncertainties due to the need to precisely predict the range in patients (Lomax, 2008a, 2008b; Paganetti, 2012; Unkelbach et al., 2009). The range uncertainty is particularly important in lung due to the low density of lung tissue and high-density areas in the beam path such as ribs. For this site it has been shown that analytical dose calculation algorithms as available in proton planning systems are significantly less accurate than Monte Carlo (MC) simulations (Grassberger et al., 2014; Schuemann et al., 2015; Yamashita et al., 2012; Zheng et al., 2016; Zvolanek et al., 2017). Precise dose calculations and plan evaluation with MC methods is therefore important for proton therapy for non-small cell lung cancer (NSCLC).

The low convergence rate of MC methods has prevented researchers from studying 4D treatment planning approaches with high accuracy, thus focusing mainly on retrospective data analysis. In 4D treatment planning, each plan should be evaluated on each phase of the 4DCT, which, due to the MC simulation times, is often unpractical. However, recent developments in computing architectures, such as graphical units processors (GPU), offer the possibility to exploit the parallelizable nature of MC methods while keeping high accuracy (Jia et al., 2012; Tseung et al., 2015). Another tool necessary to study the effect of patient movement on the delivered dose distribution is deformable image registration (DIR). DIR allows the registration of the different 4DCT phases to a reference phase. The cubic B-spline algorithm has been reported to have sufficient accuracy for dose accumulation in the thorax region (Murphy et al., 2011). Fast implementations of this algorithm for GPUs allow fast registration of the 4DCT phases (Shackleford et al., 2010). As a consequence of these GPU based developments, it is now possible to perform prospective planning studies in 4D based on MC dose calculations.

The efforts found in the literature towards 4D treatment planning can be clustered in two main directions. One is to perform plan optimization on the 4DCT using time-resolved optimization matrices (Engelsman et al., 2006; Graeff, 2017). A simpler and more clinically efficient approach that has been reported to yield good results is to perform plan optimization on one or more static 3D planning CT constructed from the 4DCT that represent the moving geometry (Engelsman and Kooy, 2005; Graeff et al., 2012; Grassberger et al., 2015; Kang et al., 2007; Knopf et al., 2013; Wang et al., 2013). The goal of this work was to perform a comparison of 4DCT-based IMPT planning strategies using ITV density overwrites for NSCLC cases. Additionally, it was intended to demonstrate that such studies are feasible with high accuracy dose calculation using state of the art dose calculations techniques to improve accuracy. To this end we have developed a GPU-based framework to study 4D treatment planning approaches in IMPT for NSCLC.

In particular we studied 4 strategies for the definition of internal tumor volumes (ITVs). For all strategies, the intensities of the planning CT outside the internal gross tumor volume (IGTV) were defined by the average image projection (AIP) across the 4DCT. Within the IGTV, intensities were set according to four different intensity fillings: constant intensity fillings of 100 HU (C100) and 50 HU (C50), maximum image projection (MIP) filling, and water equivalent path length (WEPL) dependent filling. The reason behind choosing these strategies was that they have been already proposed in the literature as potentially working solutions, but they had not been compared consistently. Kang et al. (Kang et al., 2007) have compared AIP CT, free breathing CT, MIP CT and C100 filling of the IGTV within AIP CT, demonstrating that the latter gave the best results. Graeff et al. (Graeff et al., 2012) has reported that a WEPL strategy similar to the concept introduced here yields better results than a purely geometric definition of the ITV. Knopf et al. (Knopf et al., 2013) also compared a geometrical definition of the ITV contour with a WEPL-adapted definition, proving the latter to be superior; Grassberger et al. (Grassberger et al., 2015) used a C50 filling within AIP CT. Wang et al. (Wang et al., 2013) reported the MIP approach presented in their study to be the best when compared with AIP and end-exhale images. All four techniques, although some with different implementations, have been included in our study.

2. Materials and Methods

The steps followed in this study were as follow: first, targets were defined for each patient; next, for each patient, the CT intensities within the IGTV was filled following four different strategies and the intensities outside the IGTV were set to the average of the 4DCT; next, treatment plans were optimized for each strategy with the beamlets data calculated with GPU MC; finally, a 4D evaluation was performed applying GPU MC.

2.1. Patient cohort and contour definition

A set of nine NSCLC patients with a representative range of tumor volumes and movement amplitudes was used for this retrospective study under IRB-approved protocol. For each patient, the gross tumor volume (GTV) was manually contoured at end-of-expiration phase of the 4DCT (50% or p50). The clinical target volume (CTV) was defined as an isotropic 8 mm expansion of the GTV to account for microscopic disease. The internal GTV (IGTV) and internal CTV (ICTV) were defined in the maximum intensity projection (MIP) CT, encompassing the GTV and CTV in every phase of the 4DCT. Both were validated in the 4DCT by examining the entire respiratory cycle. The liver and the tumor overlapped in the MIP in one case, for which the IGTV was created as the union of the GTV in all phases. The planning target volume (PTV) was defined as a 5 mm expansion of the ICTV, accounting for patient setup and DIR uncertainties. Normal lung was defined in the planning CT as the combination of both lungs minus the IGTV and at the reference phase as the combination of both lungs minus the GTV.

Table 1 summarizes the patient cohort. Tumor volumes ranged from 2.6 to 100.0 cm³, tumor movement amplitude was between 4.5 and 30.6 mm. The dice coefficient, measuring the overlap between the tumor positions during the respiratory cycle ranged between 0.64 and 0.93, meaning that at any respiratory phase at least 64% of the tumor volume overlaps with the volume at a different phase.

Table 1.

Patient characteristics. Amplitude is peak-to-peak motion amplitude. The Dice coefficient is a measure of the minimum overlap between GTVs as defined in two phases of the 4DCT.

Patient number	GTV vol. (cm3)	Amplitude (mm)	Min. GTV Dice coefficient	Number of fields: angles
1	21.1	30.6	0.70	4: 150, 180, 220, 270
2	64.9	3.5	0.87	2: 180, 270
3	26.0	10.7	0.92	2: 90, 180
4	4.0	14.6	0.64	2: 60, 140
5	21.7	10.0	0.84	2: 100, 210
6	2.6	5.1	0.82	2: 240, 310
7	15.4	15.1	0.74	2: 50, 120
8	24.5	9.1	0.87	3: 0, 40, 270
9	100.0	6.5	0.93	2: 250, 330
Average:	31.1 ± 31.5	11.7 ± 8.1	0.8 ± 0.1	–

2.2. Strategies to define planning CTs

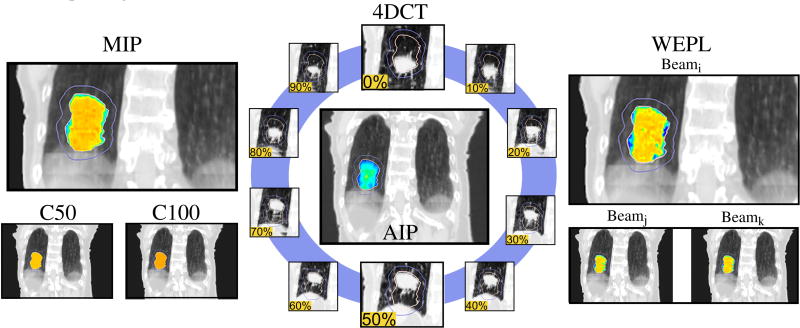
Treatment plans were designed for each patient in four different planning CTs. Each of the planning CTs was defined following a different strategy to mitigate the effect of patient movement and limit plan degradation. For all planning CTs we defined two components: the average intensity projection (AIP) of the 4DCT outside the IGTV and the intensity filling overwrite inside the IGTV. For all strategies, the intensities of the planning CT outside the IGTV were defined by the AIP. Within the IGTV, intensities were set according to four different strategies: constant intensity fillings of 100 HU (C100) and 50 HU (C50), MIP filling, and water equivalent path length (WEPL) dependent filling. Choosing the AIP around the target was a measure to balance under- and overestimations of the range to the proximal end of the target. Underestimations would then be taken into account by selecting conservative fillings of the IGTV.

In C100 and C50, the intensity values in the IGTV were set to 100 and 50 HU, respectively (expression 1). The values chosen for the constant fillings were inspired by literature, from previous studies on 4D planning (Grassberger et al., 2013; Kang et al., 2007) and studies of tissue changes after treatment, where values of 50–100 HU are shown to represent tumor intensities (Mayer et al., 1998; Akimoto et al., 2015). From the cohort here included, the chosen values have been observed to be close representations of the 99 and 70 percentiles of intensity distribution of the GTV of all patients on all phases combined. Specifically for our patients, these values correspond to 99 and 48 HU. Therefore, the two selected values represent two conservative measures of GTV intensities (figure 2c). Both referenced 4D studies have reported the constant fillings to maintain tumor coverage at acceptable dose to normal tissue. C100 is more conservative than C50 in terms of maintaining target dose levels to plan quality, but with potentially higher OAR doses.

$$I_i=100\text{ or }{I}_i=50\forall i\in \text{IGTV}$$ (1)

Figure 2.

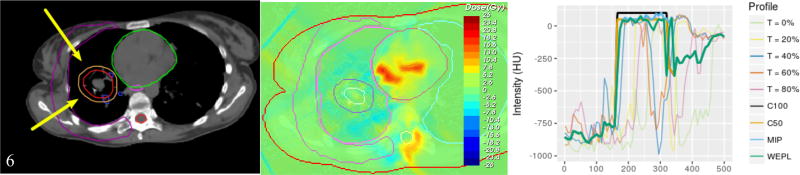
a) Structures and field arrangements for patient 6. b) Dose difference between the planned and the 4D evaluated dose for the MIP strategy. c) Intensity profiles on a line across the phases of the 4DCT.

The MIP filling sets each voxel in the IGTV to its maximum intensity across the 4DCT phases (expression 2). Due to the tumor densities observed across the patients, the MIP filled IGTV usually presents lower intensities than the constant fillings, although in some points it may have higher intensities. The MIP essentially selects the most conservative intensity value across the phases. The scope of the technique is therefore limited to changes in the IGTV.

$$I_i=\text{max}(I_{i,p})\forall i\in \text{IGTV},p\in 4\text{DCT}$$ (2)

The WEPL adjusted target sets the intensity of each voxel in the IGTV to the intensity it has in the 4DCT phase presenting the biggest WEPL at the voxel position. (expression 3). The procedure is as follows: first, the WEPL is calculated per each voxel in each phase, secondly the WEPLs are compared and lastly the voxel is set to the intensity corresponding to the biggest WEPL. This method considers CT intensities outside of IGTV region on a phase by phase basis, because the WEPL is integrated along the beam path. Consequently, this strategy defines a planning CT per treatment field. The resultant intensity values in the IGTV are, by definition, equal or smaller than the intensity values set with the MIP method.

$$I_i=I_{i,p}\text{ where }{I}_{i,p}=\underset{I_{i,p}}{\text{argmax}}\text{ WEPL}(I_{i,p})\forall i\in \text{IGTV},p\in 4\text{DCT}$$ (3)

Figure 1 illustrates the strategies differences.

Figure 1.

Illustration of planning strategies: Each planning CT (C50, C100, MIP, WEPL) was created from the 4DCT (blue circle) and its average image projection (AIP, center). The AIP was applied outside the IGTV, while the IGTV filling depends on the strategy. A color scale was added in the IGTV to help the reader, representing low intensities with blue and higher with red. Images extracted from patient 1.

2.3. Treatment planning

For each patient, 4 IMPT plans were created using the different planning CTs described above. The prescription dose was 70 Gy(RBE), delivered to at least 99% of the ICTV and 95% of the PTV. Dose was limited in both target structures to V110 ≤ 20%. Normal tissue constraints (Marks et al., 2010) were satisfied in all plans. Specifically for the lung, the mean dose was kept below 20 Gy(RBE) and V20 < 30%. Hotspots were avoided in the esophagus and spinal cord. The beams were chosen as orthogonal to the main motion direction (superior-inferior). Most cases consisted of two coplanar fields. Gantry angles were chosen to minimize normal tissue dose and to avoid placing a critical structure at the distal end of the beam. A constant RBE of 1.1 was used.

Table 1 shows the field angles for each patient. Figure 2a shows patient 6 structures and fields arrangement. Figure 2b shows the dose difference between the plan and the 4D evaluation using the results from the same patient. Figure 2c shows the intensity profiles across the 4DCT phases and the intensity profiles assigned by each strategy.

All dose calculations were performed with gPMC, a previously validated fast Monte Carlo (MC) for graphics processing units (GPU) (Qin et al., 2016). gPMC was employed to generate the dose-influence matrix (d_ij) of each field in each planning CT. IMPT optimization of the d_ijs was performed with Opt4D, an in-house optimization tool originally developed for temporo-spatial studies (Trofimov et al., 2005).

2.4. Evaluation

For evaluation, each plan was split into 10 subplans, one for each 4DCT phase. Dose for each subplan was computed on the corresponding phase, and finally the total dose was accumulated. The subplans were generated using a model of the beam delivery time structure at our institution and assuming a fixed duration per 4DCT phase of 0.5 s. To avoid a bias in the results caused by the interplay effect, we performed 10 times rescanning by setting the initial respiratory phase during the assignment to the subplans at every 4DCT phase and averaging the subplan dose. This corresponds to 10× phase-averaged rescanning and has been shown to eliminate the effect (Grassberger et al., 2013; Seco et al., 2009). The dose delivered by each subplan was then accumulated into the reference phase. The dose was warped with vector fields generated by DIR between each phase and the reference. The DIR and the dose warping were performed in Plastimatch, an open source suite for radiotherapy and medical imaging, using its GPU parallelized B-spline algorithm (Shackleford; Shackleford et al., 2010). The correctness of the registrations was visually verified.

Target coverage was evaluated in the CTV of the reference phase after 4D simulation and dose accumulation. The metrics analyzed were D99, V110 and D5-D95. Normal lung was evaluated with mean lung dose (MLD), maximum dose and V20Gy(RBE). Maximum dose was used for the spinal cord and esophagus. Strategy comparison was performed after 4D evaluation. Because the same set of objectives and constrains are applied for all the strategies, the final 4D-evaluated dose distribution is the only measure of the goodness of each strategy.

Specific comparisons between strategies were performed. The patient-by-patient difference between strategies for a given quantity X was calculated and one-tailed paired t-tests to compare the resultant distribution were applied (H₀: mean(x_j − x_i) > 0 or mean(x_j − x_i) < 0, depending on the case). This approach is discussed in detail in the following section.

3. Results and Discussion

Assessing the performance of the different strategies can be approached in two ways, either with the study of the relative changes between the plan and the 4D accumulated dose or the absolute plan performance at 4D evaluation.

When studying plan changes, there is an inconsistency in the plan baseline. Because each strategy is designed with different densities in the target, different spots will be selected by the optimizer to deliver the most optimal dose. This causes the plan dose distribution to be different for different strategies within the same patient. As such, accidental differences in plan quality arise between strategies, yielding no well-defined baseline per patient to study plan changes. Additionally, the facts that proton dose distribution is very sensitive to patient density heterogeneities (Schuemann et al., 2014) and that the planning CTs are somewhat an artificial construct, suggest that the planned dose distribution is as well an artificial construct. Hence, studying its change might not be meaningful. Therefore, as introduced in the previous section, strategy comparisons we performed after 4D evaluation. The results are summarized in table 2.

Table 2.

Strategy averages across patients per contour and dose metric. WEPL in absolute values, others as a difference with respect to WEPL values. One tailed paired t-tests where perform to assess the significance of the difference between strategies, with null hypothesis H₀: mean(x_i − x_WEPL) > 0.

Structure	Metric Gy(RBE), unless specified		Strategy
			WEPL (absolute)	MIP		C50		C100
				(average absolute difference w.r.t. WEPL and p-value)
CTV	D99		69.2 ± 4.0	−0.3 ± 0.9	0.92	−3.3 ± 2.8	>0.99	−3.3 ± 2.8	>0.99
	V110	(%)	2.7 ± 6.1	2.1 ± 3.1	0.04	6.9 ± 9.8	0.03	8.9 ± 13.6	0.04
	D5-D95		3.9 ± 2.0	1.1 ± 1.7	0.05	4.9 ± 3.7	<0.01	5.2 ± 4.0	<0.01
Lung	D̅		6.9 ± 2.6	0.1 ± 0.1	0.09	0.2 ± 0.4	0.06	0.3 ± 0.5	0.06
	V20Gy(RBE)	(%)	11.9 ± 4.6	0.2 ± 0.3	0.08	0.8 ± 1.3	0.04	1.0 ± 1.4	0.04
	Dmax		76.7 ± 3.0	1.1 ± 1.3	0.02	5.3 ± 5.2	0.01	5.2 ± 4.5	<0.01
Spinal Cord	Dmax		7.8 ± 13.5	1.4 ± 2.8	0.08	3.5 ± 7.0	0.09	3.9 ± 7.1	0.07
Heart	V25Gy	(%)	6.3 ± 10.4	−0.2 ± 1.1	0.64	0.2 ± 0.5	0.12	0.5 ± 0.4	0.01
	(without Pat. 6)		2.6 ± 3.6	0.2 ± 0.4	0.13	0.4 ± 0.4	0.03	0.5 ± 0.5	0.02
Esophagus	Dmax		15.1±18.0	1.5 ± 1.7	0.02	2.1 ± 8.0	0.24	1.8 ± 7.5	0.26

The boxplots in this section show the 1^st (Q₁), 2^nd (Q₂) and 3^rd (Q₃) quartiles with the colored box, the lower fence is the smallest observation bigger than Q₁ − 1.5 · IQR and the upper fence is the largest observation smaller than Q₃ + 1.5 · IQR. The IQR is the inter-quartile range (Q₃ − Q₁). The two fences are shown with the vertical lines. Data points beyond the fences are outliers. Individual patient points have been plotted over the boxplots to allow outlier identification.

3.1. Framework performance

4D plan simulation with GPU MC takes an average of 5 minutes per patient on one GPU unit (NVIDIA Tesla K40C). The total process, including DIR of the 4DCT phases to the reference phase takes place in 10 minutes if serial calculations are performed. Parallel calculations in a cluster could speed up the process considerably. Both, MC and DIR could be parallelized on multiple CPUs to perform the 4D plan evaluation in less than 1 minute.

3.2. Target coverage

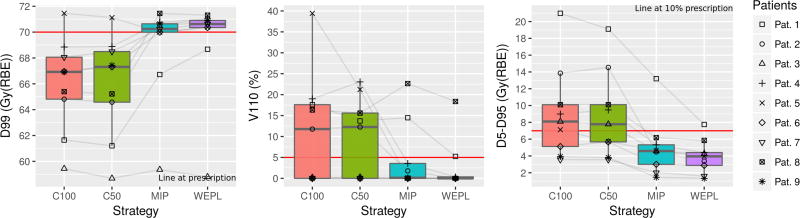
Figure 3 shows the target coverage metrics for each strategy after 4D dose simulation. In all metrics C100 and C50 have been observed to perform more poorly than the MIP and WEPL strategies.

Figure 3.

Target (CTV) coverage metrics. From left to right: D99, V110 and D5-D95. C100 and C50 provide inappropriate coverage. MIP and WEPL provide coverage, having WEPL a higher D99 index and lower V110 and D5-D95.

The delivered D99 meets at least the prescription dose in 7 out of 9 cases (77.7%) planned with the MIP and WEPL strategy. The average D99 with the MIP and WEPL strategies were 68.9 ± 3.8 and 69.2 ± 4.0 Gy(RBE), respectively. The 2 patients not fulfilling the prescribed dose present an average D99 = 63.4 Gy(RBE), 9.4% below prescription. Performing the MIP and WEPL comparison as described at the beginning of this section shows that the WEPL strategy consistently yields a higher D99 (p = 0.08).

V110 was also similar for the MIP and WEPL strategies. Their average V110 were 4.7 ± 8.2 and 2.7 ± 6.1 %, respectively. Most cases show a V110 below 5% of prescription dose. The WEPL strategy produces less hotspots than the MIP strategy (p = 0.04), which results in a higher average D5-D95 for the MIP strategy than for the WEPL, with 5.0 ± 3.4 and 3.9 ± 2.0 Gy(RBE). The WEPL strategy produces more homogeneous dose than the MIP (p = 0.05).

Patient 1 was the only outlier in all three target metrics with the MIP and WEPL strategies. As shown in table 1, this case presents the biggest amplitude in the patient cohort with 30.6 mm, which may explain the observed behavior. In this case, the WEPL strategy has a higher V99 than the MIP, with 95.3% and 82.1%, respectively, but is insufficient to provide target coverage.

3.3. Lung dose

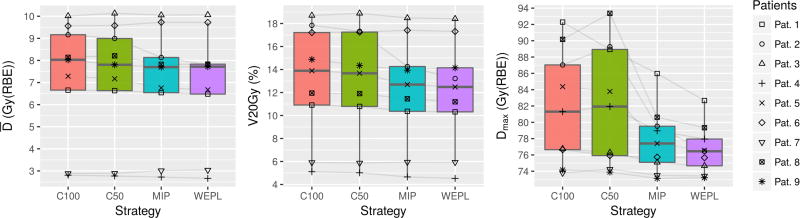
Figure 4 shows the mean lung dose (left), V20Gy(RBE) (center) and maximum dose (right) for each strategy after 4D dose simulation and accumulation. The difference between strategies is not as clear as in the target dose levels (figure 3). Still, C100 and C50 are seen to perform poorer than the MIP and WEPL strategies, giving higher MLD, V20Gy(RBE) and maximum dose. The maximum lung dose is not a clinical constraint but it serves to estimate the magnitude of hotspots that could arise in normal tissue close to the target, where other critical structures such as esophagus might be located in certain patients.

Figure 4.

Lung dose metrics. From left to right: mean dose, V20Gy(RBE) and Max dose. Lower dose levels are given by the WEPL strategy.

The MLD is kept by all strategies below 20 Gy(RBE) and V20Gy(RBE) is also below 30%, fulfilling the plan constrains. The average MLD for C100, C50, MIP and WEPL are 7.2 ± 2.7, 7.1 ± 2.7, 6.9 ± 2.6 and 6.9 ± 2.6 Gy. The MLD ranges from 2.7 to 10.1 Gy(RBE).

Hotspots are present in normal lung when employing C100 and C50 (fig. 4(c)). MIP and WEPL reduce the hotspots. Comparing MIP and WEPL, the latter produces lower MLD, V20Gy(RBE) and maximum dose (p = 0.09, p = 0.09 and p = 0.02, respectively).

3.4. Impact on other OARs

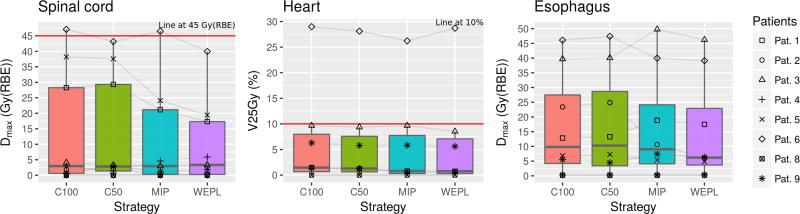
Dose to OARs downstream the target, mainly the heart, esophagus and spinal cord, depends on the specific combination of tumor movement, spot maps and beam angles. As such, the dose per patient in these OARs presented a wide range. This can be seen in figure 5.

Figure 5.

Dose metrics for spinal cord, heart and esophagus. From left to right: max dose to spinal cord, V25Gy(RBE) in the heart and max dose to esophagus. Lower dose levels are given by the WEPL strategy.

The maximum dose to the spinal cord is kept within the constraints for all patients by C50 and WEPL, as shown in Fig. 5(left). The average maximum dose is, however, significantly lower in the WEPL case than in C50: 9.8 ± 13.5 and 13.3 ± 17.9 Gy(RBE). MIP and WEPL are the strategies with lowest average maximum doses. The dose level for MIP is 11.2 ± 16.2 Gy(RBE). The patient-by-patient comparison shows the WEPL gives smaller maximum dose to the spinal cord (p = 0.08).

As shown in figures 5(center) and 2b, patient 6 presents hotspots in the heart, spinal cord and esophagus as a result of tumor movement. However, it is only in the case of the heart that patient 6 can be considered an outlier. The fact that the WEPL strategy has a higher V25Gy(RBE) for this patient increases its average, thus making it higher than with the MIP strategy. Removing this patient from the analysis shows that the WEPL strategy consistently produces lower V25Gy(RBE) in the heart than the MIP (p = 0.13). In summary, the WEPL strategy usually delivers less dose (V25Gy(RBE)) to the heart than the other strategies. The WEPL strategy also limits the average maximum dose in the esophagus.

3.5 Discussion

As shown in figures 3, 4, 5 and table 2, the WEPL strategy is superior to the MIP, C50 and C100 strategies in the current study. Target coverage is provided by the WEPL and MIP strategies, with less overdose given by the WEPL. The dose to OARs was kept lower by the WEPL strategy as well. OARs other than the lung show big differences between patients, but, with some outliers, the WEPL strategy consistently showed better dose metrics.

The fundamental idea behind the WEPL strategy here studied has already been introduced previously (Graeff et al., 2012, Knopf et al., 2013). In any WEPL-dependent approach, field specific information has to be included in the planning process, either before or after the creation of the D_ij for optimization. In the approach by Knopf et al., field specific ITVs as a function of the WEPL are generated making the D_ij agnostic of the movement information. However, the lack of a common or generalized target contour implies a limitation for IMPT planning as it can only be jointly optimized using single field uniform dose (SFUD) conditions or by joining the ITVs, considerably augmenting the target volume. On the other hand, the methods by Graeff et al. and the one introduced in our work include the movement information in the optimization matrix itself, providing a well-defined target for full IMPT optimization. The only difference between the two approaches is that, contrary to our approach, Graeff et al. define adapted intensity-WEPL conversion curves for each beamlet in each field. These curves scale the WEPL seen inside the target by the dose calculation algorithm to cover the minimum and maximum WEPL found along the beamlet across the phases of the 4DCT. After being calculated with this curve, each beamlet is included in the D_ij for optimization. This method, depending on the specific implementation, should yield similar results to the WEPL method presented in this manuscript, although out approach is simpler. Note that, if the plans are done with the SFUD method, all three WEPL dependent methods will yield very similar results.

In order to apply the WEPL method here discussed, the treatment planning system has to be able to deal with as many CTs as fields in the plan during the D_ij calculations.

One main caveat in this study is the assumption that the 4DCT is a good representation of the breathing pattern of the patient at treatment time. Some studies have reported significant changes in the tumor baseline and tumor motion pattern as the treatment progresses (Phillips et al., 2015; Takao et al., 2016; Yi et al., 2011; Zhang et al., 2013). Some deformation of the tumor may also occur during this time (Yi et al., 2011). These effects are not captured in the current study design, which relies on the 4DCT. Nevertheless, from the data presented in this study it can be hypothesized that the MIP and WEPL strategies are the most robust towards these changes as well. As shown in figure 2c, strategies C100 and C50 are the most conservative because they force the optimizer to employ beamlets with higher energy due to the higher density overwrite. Therefore, they could be expected to be more robust than MIP and WEPL against patient geometry changes not captured in the 4DCT that involve an increase in patient water-equivalent thickness from beam’s eye view. Nevertheless, even in this case, being C100 and C50 more robust does not mean that their plan quality would be superior to the MIP and WEPL strategies because the performance baseline, as studied in this manuscript, is better in the latter strategies. More importantly, in lung cancer, especially during a prolonged treatment regimen with concurrent chemotherapy, tumor shrinkage is usually more likely, which would lead to more beamlets being placed behind the target in the constant overwrite strategies (C50/100). The same argument could potentially be employed with other patient-specific constant fillings. Any constant filling strategy would be deduced mainly from the study of the tumor intensity spectra across the 4DCT, ultimately simplifying it to a single point. On the contrary, non-constant fillings do not show this limitation, hence including more information. In summary, the robustness of these strategies towards patient changes should be compared, although the authors do not expect differences in plan degradation to overcome the plan quality baseline differences seen in this study. Other constant filling strategies remain to be investigated; however, the authors do not expect an improvement on the MIP or WEPL strategies analyzed herein.

4. Conclusions

Respiratory motion degrades the planned IMPT dose distribution. Four strategies to limit the plan degradation produced by the patient’s respiratory motion were studied using state of the art Monte Carlo simulations. A fast GPU-framework was developed for treatment planning and 4D dose evaluation. Of the four considered strategies, the AIP of the 4DCT along with the WEPL-dependent IGTV filling best capture different patient geometries represented in the 4DCT in one planning CT. This strategy keeps prescription dose levels to the target, while maintaining low dose to OARs. The WEPL strategy is accordingly recommended as a good approach in any case involving collapsing different patient geometries, such as respiratory phases, into a representative construct. Concerning its applicability, the treatment planning system has to be able to handle as many CT volumes as fields in the plan for the generation of the optimization matrices. No other no special requirements are necessary for the IMPT optimization.

Additionally, we show that it is possible to assess the quality of a treatment plan on 4D geometries on a patient-per-patient basis with high accuracy calculations. Assuming the 4DCT is a representative geometry of the patient’s breathing cycle during delivery, the developed GPU MC framework could be implemented as a treatment plan validation of NSCLC proton therapy.