Major influence of a ‘smoke and mirrors’ effect caused by wave reflection on early diastolic coronary arterial wave intensity

Abstract

Key points

• Coronary wave intensity analysis (WIA) is an emerging technique for assessing upstream and downstream influences on myocardial perfusion.

• It is thought that a dominant backward decompression wave (BDW_dia) is generated by a distal suction effect, while early‐diastolic forward decompression (FDW_dia) and compression (FCW_dia) waves originate in the aorta.

• We show that wave reflection also makes a substantial contribution to FDW_dia, FCW_dia and BDW_dia, as quantified by a novel method. In 18 sheep, wave reflection accounted for ∼70% of BDW_dia, whereas distal suction dominated in a computer model representing a hypertensive human.

• Non‐linear addition/subtraction of mechanistically distinct waves (e.g. wave reflection and distal suction) obfuscates the true contribution of upstream and downstream forces on measured waves (the ‘smoke and mirrors’ effect).

• The mechanisms underlying coronary WIA are more complex than previously thought and the impact of wave reflection should be considered when interpreting clinical and experimental data.

Abstract

Coronary arterial wave intensity analysis (WIA) is thought to provide clear insight into upstream and downstream forces on coronary flow, with a large early‐diastolic surge in coronary flow accompanied by a prominent backward decompression wave (BDW_dia), as well as a forward decompression wave (FDW_dia) and forward compression wave (FCW_dia). The BDW_dia is believed to arise from distal suction due to release of extravascular compression by relaxing myocardium, while FDW_dia and FCW_dia are thought to be transmitted from the aorta into the coronary arteries. Based on an established multi‐scale computational model and high‐fidelity measurements from the proximal circumflex artery (Cx) of 18 anaesthetized sheep, we present evidence that wave reflection has a major impact on each of these three waves, with a non‐linear addition/subtraction of reflected waves obscuring the true influence of upstream and downstream forces through concealment and exaggeration, i.e. a ‘smoke and mirrors’ effect. We also describe methods, requiring additional measurement of aortic WIA, for unravelling the separate influences of wave reflection versus active upstream/downstream forces on coronary waves. Distal wave reflection accounted for ∼70% of the BDW_dia in sheep, but had a lesser influence (∼25%) in the computer model representing a hypertensive human. Negative reflection of the BDW_dia at the coronary–aortic junction attenuated the Cx FDW_dia (by ∼40% in sheep) and augmented Cx FCW_dia (∼5‐fold), relative to the corresponding aortic waves. We conclude that wave reflection has a major influence on early‐diastolic WIA, and thus needs to be considered when interpreting coronary WIA profiles.

Key points

• Coronary wave intensity analysis (WIA) is an emerging technique for assessing upstream and downstream influences on myocardial perfusion.

• It is thought that a dominant backward decompression wave (BDW_dia) is generated by a distal suction effect, while early‐diastolic forward decompression (FDW_dia) and compression (FCW_dia) waves originate in the aorta.

• We show that wave reflection also makes a substantial contribution to FDW_dia, FCW_dia and BDW_dia, as quantified by a novel method. In 18 sheep, wave reflection accounted for ∼70% of BDW_dia, whereas distal suction dominated in a computer model representing a hypertensive human.

• Non‐linear addition/subtraction of mechanistically distinct waves (e.g. wave reflection and distal suction) obfuscates the true contribution of upstream and downstream forces on measured waves (the ‘smoke and mirrors’ effect).

• The mechanisms underlying coronary WIA are more complex than previously thought and the impact of wave reflection should be considered when interpreting clinical and experimental data.

Introduction

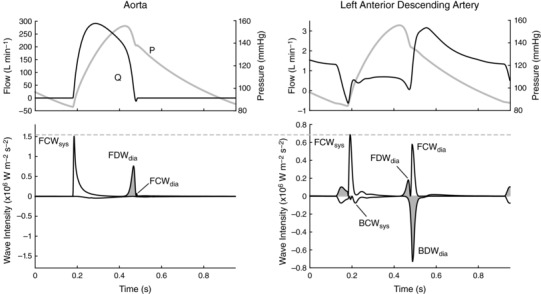
Wave intensity analysis (WIA) has been used to study the upstream and downstream forces contributing to the distinctive pattern of coronary arterial blood flow (Sun et al. 2000, 2004; Davies et al. 2006a; Hadjiloizou et al. 2008; Smolich & Mynard, 2016), with ‘waves’ (i.e. incremental changes in blood pressure and velocity) arising from active forces such as myocardial contraction/relaxation or from wave reflection. Given the diastolic dominance of coronary arterial flow, there has been particular interest in the wave dynamics underlying the early‐diastolic flow surge and how waves around this time are affected by various forms of heart disease and medical intervention (Davies et al. 2006a, 2011; Kyriacou et al. 2012; Lockie et al. 2012; De Silva et al. 2013; Claridge et al. 2015). Three main waves have been consistently identified during this early‐diastolic phase of the cardiac cycle (Fig. 1). [In this paper ‘early‐diastole’ refers to the period soon after the left ventricle starts to relax, and hence encompasses the short period before aortic valve closure, sometimes referred to as protodiastole.] A flow‐increasing backward decompression wave (BDW_dia) is believed to arise from the release of extravascular compressive forces on intramyocardial vessels, producing a suction effect that propagates back towards the coronary ostium (Davies et al. 2006a). In addition, two forward waves, a flow‐decreasing forward decompression wave (FDW_dia) and a flow‐increasing forward compression wave (FCW_dia), are thought to arise from transmission of corresponding aortic waves into the coronary arteries; these aortic waves are generated by the early diastolic fall in left ventricular (LV) cavity pressure and the pressure/flow ‘rebound’ caused by aortic valve closure respectively (Davies et al. 2006a).

Figure 1. Circumflex coronary pressure (P), flow (Q) and wave intensity from an adult sheep.

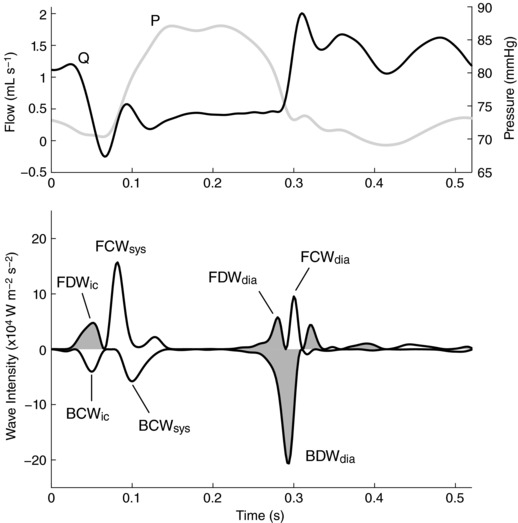
The major waves, which are also present in humans, are labelled according to wave type (FCW, FDW, BCW, BDW; forward/backward compression/decompression wave) and phase of the cardiac cycle (ic, isovolumic contraction; sys, early‐systole; dia, early‐diastole). Decompression (i.e. pressure‐decreasing) waves are shaded.

While the current explanations for early‐diastolic coronary arterial waves are intuitive, they have not been confirmed by any direct approach, while close inspection of published coronary WIA data suggest that the picture is not yet complete. Specifically, although correlations have been observed between BDW_dia magnitude and indices of isovolumic relaxation derived from LV cavity pressure, the reported R ² values (0.21–0.35) suggest that more than 60% of the variability in BDW_dia magnitude is currently unexplained (Kyriacou et al. 2012; Ladwiniec et al. 2016). Indeed, it is unclear why the BDW_dia is much larger than a backward compression wave occurring during isovolumic contraction (BCW_ic, Fig. 1), despite published data suggesting that the rate of change of intramyocardial pressure rise (leading to BCW_ic) and fall (leading to BDW_dia) are comparable (Heineman & Grayson, 1985; Stein et al. 1985; Rabbany et al. 1989). In addition, although it is generally assumed that the FDW_dia and FCW_dia are simply transmitted from the aorta into the coronary arteries (Davies et al. 2006a), several published figures suggest that the FDW_dia and FCW_dia may be less and more prominent, respectively, in the coronary arteries than aorta (Hughes et al. 2008; Lu et al. 2012), with the basis of such differences yet to be defined.

A potentially significant but largely unexplored factor that may influence the early‐diastolic coronary waves is wave reflection, with backward waves reflecting proximally at the coronary ostium and forward waves reflecting distally in the coronary arterial network. Due to the large impedance mismatch between the coronary arteries and aorta (Davies et al. 2006a), the BCW_ic is considered to undergo near‐complete negative reflection at the coronary ostium, leading to a subsequent forward decompression wave (FDW_ic, Fig. 1); however, it is unclear whether the BDW_dia also undergoes such reflection and what effect this might have on the FCW_dia and FDW_dia. In addition, partial reflection of the early‐systolic forward compression wave (FCW_sys) in the coronary arterial bed leads to a second backward compression wave (BCW_sys), but it is unclear whether the FDW_dia is similarly reflected, and whether the resulting reflected decompression wave might contribute to the BDW_dia.

The foregoing phenomena have particular relevance due to the possibility that a measured wave intensity peak (herein referred to as a ‘wave’) may arise from a combination of factors, such as the simultaneous influence of an active force and wave reflection. Intuitively, the combination of two mechanistically distinct waves would be expected to have an additive effect if both waves are compression waves or both are decompression waves, or a cancelling effect if compression and decompression waves combine. However, the specific nature of such additive or cancelling effects, and a method for unravelling the separate contributions of an active force and wave reflection to a composite wave, have yet to be defined.

The aim of this study was to investigate the extent to which each of the three main early diastolic coronary waves, currently presumed to simply arise from upstream (FDW_dia and FCW_dia) and downstream (BDW_dia) active forces (Davies et al. 2006a), are also influenced by wave reflection. We first demonstrate that there is a non‐linear additive or cancelling effect on wave intensity when two mechanisms contribute to a measured wave. Using a previously described multi‐scale computational model of the coronary circulation (Mynard et al. 2014; Mynard & Smolich, 2016a), we show that wave reflection effects lead to concealment of the coronary FDW_dia and augmentation of the BDW_dia and FCW_dia, which we term a ‘smoke and mirrors’ effect. We also describe methods for unravelling the contributions of active forces and wave reflection underlying measured coronary waves. These principles and methods were initially tested with the computational model and then examined in an experimental model where simultaneous aortic and coronary WIA were obtained under baseline conditions and following an increase in arterial blood pressure, with or without coronary vasoconstriction.

Methods

Ethical approval

Experimental studies (described towards the end of this section) were approved by the Monash University Animal Ethics Committee and conformed to the guidelines of the National Health and Medical Research Council of Australia.

Wave intensity

Wave intensity is defined as the product of incremental changes in pressure and velocity (dPdU) (Parker & Jones, 1990). Since this quantity is sample time‐dependent, a time‐corrected wave intensity is often used, calculated as WI = (dP/dt)(dU/dt) (Ramsey & Sugawara, 1997; Penny et al. 2008). The forward component (WI₊) and backward component (WI₋) of wave intensity are calculated via WI_± = ±(dP/dt ± ρc dU/dt)²/(4ρc), with forward waves having positive WI and backward waves having negative WI. Cumulative wave intensity (CI), related to the energy of a wave (Davies et al. 2006a; Mynard & Smolich, 2016b), is defined as the integral of WI_± over the duration of a given wave. Waves that have a pressure‐increasing effect are called ‘compression waves’, whereas waves that have a pressure‐decreasing effect are called ‘decompression waves’ (sometimes also referred to as ‘suction’ or ‘expansion’ waves). The four possible wave types are forward compression (FCW), forward decompression (FDW), backward compression (BCW) and backward decompression (BDW) waves.

Non‐linear addition and subtraction of coronary waves

Since coronary arterial waves may arise from an active mechanism (e.g. a distal suction effect arising in the intramyocardial vessels) and also from wave reflection, it is possible that both phenomena could simultaneously influence the wave intensity profile. In this section, we show that the addition or subtraction of two mechanistically distinct waves is non‐linear (i.e. 1 + 1 ≠ 2). For simplicity of notation, in this section we use the non‐time‐corrected form of wave intensity, but the same principles also apply to the time‐corrected form.

Consider the situation where two waves propagate in the same direction, but one arises via passive reflection of some incident wave (dPdU _reflected) and the other is generated from an active process such as a change in extravascular pressure due to myocardial relaxation (dPdU _active). If these two mechanistically distinct waves affect pressure and velocity at the same time, the total change in pressure will be dP _reflected + dP _active and the total change in velocity will be dU _reflected + dU _active. The wave intensity of the resulting combined wave is therefore

$$\begin{array}{ccc}\hfill \mathrm{d}P\mathrm{d}{U}_{\mathrm{combined}}& =& (\mathrm{d}{P}_{\mathrm{reflected}}+\mathrm{d}{P}_{\mathrm{active}})(\mathrm{d}{U}_{\mathrm{reflected}}\hfill \\ & & +\mathrm{d}{U}_{\mathrm{active}})\hfill \end{array}$$ (1)

Importantly, we see that these waves do not add linearly, that is

$$\mathrm{d}P\mathrm{d}{U}_{\mathrm{combined}}\ne \mathrm{d}P\mathrm{d}{U}_{\mathrm{reflected}}+\mathrm{d}P\mathrm{d}{U}_{\mathrm{active}}$$ (2)

For example, consider two backward decompression waves (BDW₁ and BDW₂) for which dP and dU have numerical values of −5 and 5 respectively for both waves, with BDW₁ arising from wave reflection and BDW₂ arising from myocardial relaxation (Fig. 2 A). Wave intensity of each wave in isolation would be −25 (dPdU = −5 × 5). However, if these two waves occur at the same time, the resulting combined BDW will not have an amplitude of −50, but rather dPdU _combined = (−5 − 5) × (5 + 5) = −100. This illustrates the principle that when two compression waves or two decompression waves combine, the resultant wave is much larger than the sum of the contributing waves in isolation.

Figure 2. Illustration of non‐linear wave addition and subtraction.

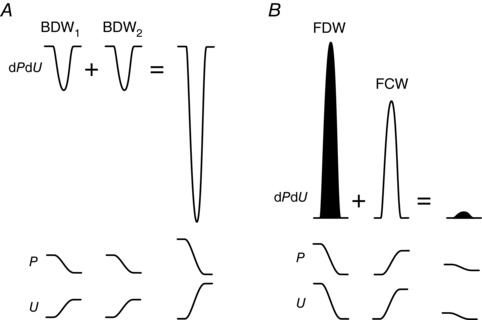
A, when two backward decompression waves (BDW₁ and BDW₂) combine, the wave intensity (dPdU) of the resultant single combined wave is greater than the sum of the dPdU of the two waves in isolation. B, when a forward decompression wave (FDW) combines with a forward compression wave (FCW), there is a non‐linear cancelling effect. The non‐linear nature of wave intensity addition and subtraction may be understood by assessing the underlying pressure (P) and velocity (U) changes associated with the waves.

Now consider what happens if two waves with opposing pressure effects combine. For example, if an FDW with wave intensity dPdU = −5 × −6 = 30 combines with an FCW with wave intensity dPdU = 4 × 5 = 20, the resulting combined wave does not have an amplitude of 20 + 30 = 50, nor is it 30 − 20 = 10; rather it is dPdU _combined = (4 − 5) × (5 − 6) = 1 (Fig. 2 B). Thus, there is a non‐linear cancelling effect when a compression wave combines with a decompression wave.

Coronary reflection and myocardial contraction/relaxation

With these principles of wave addition and subtraction in mind, we therefore tested two main hypotheses:

• Hypothesis 1 (Fig. 3 A): The measured early‐diastolic coronary BDW (BDW_dia) arises from a combination of two distinct processes, (i) an active suction effect caused by a rapid fall in vascular external compression due to myocardial relaxation (mr), which in isolation would cause a backward decompression wave designated BDW_mr; and (ii) passive distal reflection of the early diastolic FDW transmitted from the aorta into the coronary arteries (FDW_A→C), which in isolation would cause a wave designated BDW_ref. The BDW_mr and BDW_ref add non‐linearly to produce the BDW_dia, which is thus substantially larger than the sum of the intensities of the individual waves. This hypothesis is illustrated in Fig. 3 A.

• Hypothesis 2 (Fig. 3 B): The coronary BDW_dia undergoes almost complete negative reflection when it reaches the coronary ostium due to the much lower impedance of the aorta compared with the coronary artery. The resulting reflected FCW (FCW_ref) has a non‐linear cancelling effect on the aortic FDW transmitted into the coronary arteries (FDW_A→C), with the resultant measured coronary wave (FDW_dia) being relatively small compared with aortic FDW_dia. In addition, the FCW_ref has a non‐linear additive effect on the FCW related to valve closure that is transmitted from the aorta into the coronary arteries (FDW_A→C), with the resultant combined coronary wave (FDW_dia) being relatively large compared with aortic FDW_dia. This hypothesis is illustrated in Fig. 3 B.

Figure 3. Illustration of the mechanisms underlying early diastolic coronary waves.

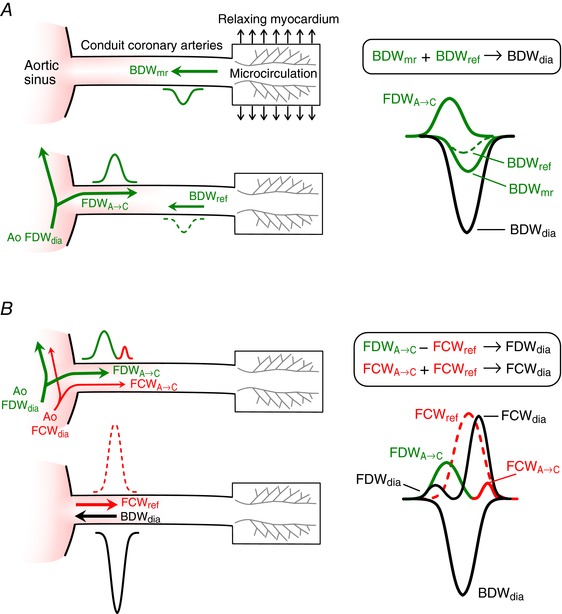
A, the measured BDW_dia arises in part from a distal suction effect caused by myocardial relaxation (BDW_mr); a second contribution to BDW_dia arises from distal reflection (BDW_ref) of the aortic forward decompression wave (Ao FDW_dia) that passes into the coronary arteries (FDW_A→C). The BDW_mr and BDW_ref add non‐linearly to produce a prominent BDW_dia. B, the BDW_dia undergoes near‐complete negative reflection at the coronary ostium, where it encounters a large drop in characteristic impedance. This produces a reflected forward compression wave (FCW_ref) that non‐linearly subtracts from the FDW_A→C and augments the valve closure‐related forward compression wave (FCW_A→C) that originates in the aorta (Ao FCW_dia), leading to the measured early‐diastolic forward waves (FDW_dia and FCW_dia). Measured waves are indicated in black while component compression and decompression waves are indicated in red and green respectively (colour in online version only). Waves arising from reflection are indicated with dashed lines. [Color figure can be viewed at wileyonlinelibrary.com]

Distinguishing wave reflection and upstream/downstream forces

Based on the above principles, we propose that the coronary FDW_A→C, i.e. the coronary FDW_dia that would occur in the absence of BDW_dia reflection, may be estimated by assuming that the aortic FCW_sys and FDW_dia are identically transmitted into the coronary artery, and hence the following ratios (known as transmission coefficients) should also be approximately equal:

$$\frac{\mathrm{Coronary}\mathrm{FD}{\mathrm{W}}_{\mathrm{A}\to \mathrm{C}}}{\mathrm{Aortic}\mathrm{FD}{\mathrm{W}}_{\mathrm{dia}}}\approx \frac{\mathrm{Coronary}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}}{\mathrm{Aortic}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}}$$ (3)

This may be rearranged to estimate the coronary FDW_A→C, which is the only unknown:

$$\begin{array}{ccc}\hfill \mathrm{Coronary}\mathrm{FD}{\mathrm{W}}_{\mathrm{A}\to \mathrm{C}}& \approx & \mathrm{Coronary}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}\hfill \\ & & \times \left(\frac{\mathrm{Aortic}\mathrm{FD}{\mathrm{W}}_{\mathrm{dia}}}{\mathrm{Aortic}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}}\right)\hfill \end{array}$$ (4)

In the same way, the coronary FCW_A→C may also be estimated as

$$\begin{array}{ccc}\hfill \mathrm{Coronary}\mathrm{FC}{\mathrm{W}}_{\mathrm{A}\to \mathrm{C}}& \approx & \mathrm{Coronary}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}\hfill \\ & & \times \left(\frac{\mathrm{Aortic}\mathrm{FC}{\mathrm{W}}_{\mathrm{dia}}}{\mathrm{Aortic}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}}\right)\hfill \end{array}$$ (5)

If we calculate an early systolic coronary reflection index as BCW_sys/FCW_sys and assume that the same degree of wave reflection occurs during early diastole (this assumption will be examined in the Results section using the computational model), then the BDW_ref can be estimated from FDW_A→C via

$$\begin{array}{ccc}\hfill \mathrm{Coronary}\mathrm{BD}{\mathrm{W}}_{\mathrm{ref}}& \approx & \mathrm{Coronary}\mathrm{FD}{\mathrm{W}}_{\mathrm{A}\to \mathrm{C}}\hfill \\ & & \times \left(\frac{\mathrm{Coronary}\mathrm{BC}{\mathrm{W}}_{\mathrm{sys}}}{\mathrm{Coronary}\mathrm{FC}{\mathrm{W}}_{\mathrm{sys}}}\right)\hfill \end{array}$$ (6)

Equations (4) to (6) can be applied to peak wave intensity, cumulative intensity (wave area) or incremental changes in pressure and velocity (dP _± and dU _±). The coronary BDW_mr intensity can then be estimated by (i) calculating dP ₋ and dU ₋ associated with BDW_ref, via eqn (6), (ii) calculating dP ₋ and dU ₋ associated with BDW_mr, by subtracting values for BDW_ref from values for BDW_dia, and (iii) calculating BDW_mr wave intensity as the product of the resulting BDW_mr dP ₋ and dU ₋ values. This may be expressed as

$$\begin{array}{ccc}\hfill \mathrm{Coronary}\mathrm{BD}{\mathrm{W}}_{\mathrm{mr}}& =& \mathrm{d}{P}_{\mathrm{mr}-}\mathrm{d}{U}_{\mathrm{mr}-}=(\mathrm{d}{P}_{\mathrm{dia}-}-\mathrm{d}{P}_{\mathrm{ref}-})\hfill \\ & & \times (\mathrm{d}{U}_{\mathrm{dia}-}-\mathrm{d}{U}_{\mathrm{ref}-})\hfill \end{array}$$ (7)

In this equation, dP and dU may be replaced by dP ₋/dt and dU ₋/dt for calculation of time‐corrected BDW_mr. The contribution of BDW_mr to the measured BDW_dia may then be quantified as

$$\mathrm{BD}{\mathrm{W}}_{\mathrm{mr}}\mathrm{contribution}=\frac{\mathrm{BD}{\mathrm{W}}_{\mathrm{mr}}}{\mathrm{BD}{\mathrm{W}}_{\mathrm{mr}}+\mathrm{BD}{\mathrm{W}}_{\mathrm{ref}}}$$ (8)

and expressed as a percentage, noting that this is not the same as BDW_mr/BDW_dia due to the non‐linear addition effects described above. Note that eqn (7), and hence also eqn (8), depend on instantaneous values of dP and dU and can therefore only be used in relation to peak intensity. This means that the cumulative intensity of the BDW_ref but not the BDW_mr can be estimated.

Model description

The model used in this study is based on our previous work (Mynard et al. 2012, 2014; Mynard & Smolich, 2016a). Aside from some input parameters discussed below, all aspects of the model have been described in these previous papers and we therefore provide only a brief summary below. Model parameters are provided in the Appendix.

First, a one‐dimensional (1D) model of the major right dominant conduit coronary arterial system was derived from measurements obtained in humans by Dodge et al. (1992) (Fig. 4 A). The standard non‐linear 1D equations in these networks were solved as in Mynard & Nithiarasu (2008), making use of a physiologically realistic non‐linear elastic pressure–area relationship (Mynard et al. 2012) and the approximate velocity profile method of Bessems et al. (2007) to estimate the viscous friction term.

Figure 4. Schematics of the model components.

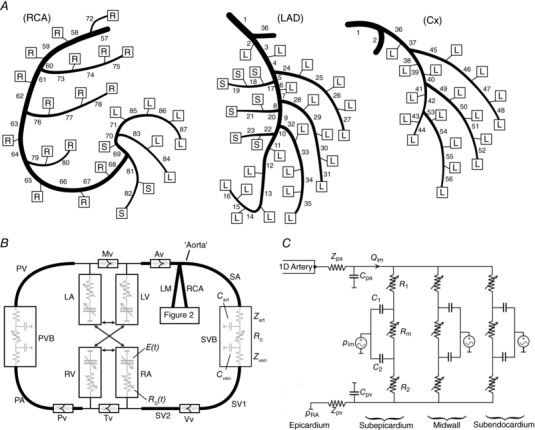
A, one‐dimensional (1D) model of the conduit coronary arteries; B, closed‐loop cardiovascular model within which the coronary model resides; C, the coronary microcirculation model. Boxes in A indicate attachment of terminal 1D segments to instances of the lumped parameter microcirculatory model shown in C, which supply parts of the right ventricular free wall (‘R’ boxes), left ventricular free wall (‘L’ boxes) or septum (‘S’ boxes). Full details of the right dominant coronary network shown in A are provided in Mynard & Smolich (2016a). Note that the proximal end of the SA segment is referred to as the aorta. Abbreviations: Av, aortic valve; Cx, circumflex coronary artery; LA, left atrium; LM, left main coronary artery; LV, left ventricle; Mv, mitral valve; PA, pulmonary artery; Pv, pulmonary valve; PV, pulmonary vein; PVB, pulmonary vascular bed; RA, right atrium; RCA, right coronary artery; RV, right ventricle; SA, systemic artery; SVB, systemic vascular bed; SV, systemic vein; Tv, tricuspid valve; Vv, venous valve.

Second, the coronary model was placed within a closed‐loop model of the cardiovascular system (Mynard et al. 2012) that included the four heart chambers and valves, lumped systemic and pulmonary vascular beds, and single 1D segments approximating each of the major vascular networks (Fig. 4 B); a similar model but with anatomically based vascular networks was described by Mynard and Smolich (2015), but this level of detail is not required for the present study.

Third, the coronary microcirculation was represented by a lumped parameter model (Fig. 4 C), instances of which were inserted at all distal outlets of the 1D conduit artery model (boxes in Fig. 4 A). This microvascular model, based on studies by Bruinsma et al. (1988) and Spaan et al. (2000), was divided into subepicardial, midwall and subendocardial layers. Each layer consisted of two compartments, whose volumes were governed by the compliances C ₁ and C ₂, approximately corresponding to small arteries and veins respectively in the layer. Each layer also contained three volume‐dependent resistances, R ₁ and R ₂, which were modulated by the volume in compartments 1 and 2 respectively, and a middle resistance (R _m) modulated by the volume in both compartments. Compartment volume depended on the difference between intravascular pressure and intramyocardial pressure (p _im). As in Mynard et al. (2014), we assumed that p _im arises from (i) cavity‐induced extracellular pressure (CEP), i.e. transmission of ventricular cavity pressure into the ventricular wall, and (ii) shortening‐induced intracellular pressure (SIP), arising from the thickening of shortening myofibrils that leads to compression of adjacent blood vessels (Heineman & Grayson, 1985; Rabbany et al. 1989; Algranati et al. 2010). For a full description of the model, including equations, see Mynard et al. (2014).

Parameters for the cardiovascular model are provided in the Appendix and were chosen to represent an older adult with stage I hypertension, typical of patients encountered in clinical studies of coronary wave intensity (Davies et al. 2006a; Hadjiloizou et al. 2008; Narayan et al. 2015), with aortic pressures of 155/84 mmHg, cardiac output 4.9 L min⁻¹, systemic vascular resistance 1.8 mmHg.s mL⁻¹ and aortic wave speed 9.0 m s⁻¹ (Mitchell et al. 2003). Distributed arterial wave reflection was approximated by introducing linear tapering in the single equivalent systemic artery. Coronary resistance was adjusted using an iterative algorithm (Mynard et al. 2014; Mynard & Smolich, 2016a) to achieve a total coronary flow equal to 4.5% of cardiac output; due to the higher perfusion pressure, a 52–90% increase in intramyocardial resistance was required compared with the original model, depending on the region and transmural layer. Note that the model was not intended to represent the sheep studied in the experimental model; rather, it was used to investigate wave dynamics in a system approximately representative of patients encountered clinically.

Model‐based analysis of coronary wave mechanisms

With the reference simulation of coronary haemodynamics established, we sought to elucidate the mechanisms underlying observed waves with two ‘virtual experiments’.

First, to identify waves generated from within the myocardium, aortic waves were prevented from passing into the coronary arteries by enforcing a reflection coefficient of −1 at the coronary ostia, achieved by prescribing a constant end‐diastolic pressure at the boundary; this maintained the same reflection conditions for backward‐running coronary waves. To ensure this did not cause any indirect changes to the intramyocardial pump effect, we also prescribed the same time‐varying intramyocardial pressures and resistances as in the reference case.

Second, to elucidate the interactions between waves transmitted from the aorta into the coronary arteries and those originating in the coronary microcirculation, we took the aortic pressure waveform from the reference case and prescribed this at the coronary inlets after applying a phase shift (i.e. time delay) that varied between −110 ms and +110 ms in 10‐ms steps (a total of 23 simulations). This meant that all aortic waves passing into the coronary arteries were variably delayed whereas waves arising from intramyocardial pump effects in the microcirculation were fixed, allowing clear identification of the origin of different waves and the effects of wave addition and subtraction.

We also tested the assumption that the coronary reflection index is similar during early systole and early diastole. Starting with the reference simulation, this was done by (i) removing the intramyocardial pressure source (p _im in Fig. 4 C) to ensure backward waves arose only via reflection and (ii) retaining the p _im‐related changes in coronary resistance from the reference simulation, noting that changes in resistance are likely to be a key factor determining the instantaneous reflection index. Then, the reflection index (BCW_sys/FCW_sys) at different times in the cardiac cycle was assessed in the proximal left anterior descending artery (LAD) by introducing delays in the incoming aortic waves. Distal reflection indexes during early systole (BCW_sys/FCW_sys) and early diastole (BDW_dia/FDW_dia) were also assessed in all terminal 1D vessels (no delays applied).

Unless otherwise stated, results are presented for the proximal LAD, since this is frequently the subject of clinical investigation, but similar findings were also obtained in other vessels, including the circumflex artery. A sensitivity analysis was performed to evaluate to what extent the contribution of wave reflection versus myocardial relaxation on BDW_dia depends on aortic mean and pulse pressures (adjusted via systemic vascular bed resistance and aortic wave speed respectively), intramyocardial resistance (parallel combination of R ₁ from all layers, see Fig. 4 C) or compliance (C ₁ and C _pa), monitoring location along the entire length of the LAD or coronary wave speed.

Experimental preparation

The experimental preparation was similar to that described previously (Penny et al. 2008). Eighteen Border‐Leicester cross ewes weighing 49.6 ± 4.8 kg (mean ± SD) were anaesthetized with an intramuscular injection of ketamine (5 mg kg⁻¹) and xylazine (0.1 mg kg⁻¹) followed by intravenous α‐chloralose (25–50 mg kg⁻¹). Anaesthesia was maintained with intravenous α‐chloralose infused at a rate of 12–25 mg kg h⁻¹. After intubation of the trachea, animals were ventilated with a large animal respirator (model 607; Harvard Apparatus, Dover, MA, USA) with ventilation adjusted to maintain arterial O₂ tension at 100–120 mmHg and arterial CO₂ tension at 35–40 mmHg. Body temperature was maintained at 39–40°C with a heating pad and towel covering.

The neck was incised in the midline, and polyvinyl catheters were advanced through the left external jugular vein to the superior vena cava for fluid and drug infusion. A 5‐Fr. micromanometer‐tipped catheter (MPC‐500; Millar Instruments, Houston, TX, USA) was inserted into the left common carotid artery, and its tip was advanced into the ascending aorta, just above the leaflets of the aortic valve, to measure high‐fidelity blood pressure. After exposure of the heart and central vessels through a left thoracotomy performed in the fourth intercostal space and incision of the pericardium over the pulmonary trunk and left atrium, cannulae were inserted through purse string sutures in the aortic arch and left atrial appendage, and connected to fluid‐filled polyvinyl tubing. Transit time flow probes (Transonics Systems, Ithaca, NY, USA) were placed around the ascending aorta (20 or 24 mm) and proximal circumflex coronary artery (2 or 4 mm). A second MPC‐500 catheter was inserted through the roof of the left atrium and passed across the mitral valve into the LV cavity.

Experimental protocol

Aortic blood pressure measured via the fluid‐filled catheter was referenced to atmospheric pressure at the level of the mid‐thoracic vertebral spines and calibrated against a manometer before each experiment. Aortic and LV micromanometers were connected to transducer control units (TCB‐500; Millar Instruments), while ascending aortic and coronary flow probes were interfaced with a flowmeter (model T206; Transonic Systems). Animals underwent one of two interventions: (i) in 11 animals, aortic blood pressure and coronary vascular resistance were increased by inhibition of NO synthesis via intravenous infusion of the stereospecific NO synthase inhibitor N ^ω‐nitro‐l‐arginine (l‐NNA, 25 mg kg⁻¹) over 10 min (Penny & Smolich, 2002); (ii) in seven animals, mean central aortic blood pressure was raised to a similar level as in the l‐NNA studies via constriction of the thoracic descending aorta and brachiocephalic trunk using adjustable snares. Recordings of 20 s duration were digitized at 500 Hz under baseline conditions, and after haemodynamics had stabilized after each intervention. At the end of the study, animals were killed with an overdose of pentobarbitone sodium (100 mg kg⁻¹).

Data analysis

Experimental data were analysed with a custom script written in Spike2 (Cambridge Electronic Design, Cambridge, UK). Signals were low pass filtered (cut‐off 48 Hz) to remove electrical interference and beat onset was defined as the time when LV pressure began to rise, detected via signal curvature according to a validated algorithm (Mynard et al. 2008). Analysis was performed on ensemble‐averaged data derived from at least 10 individual beats.

For WIA, mean blood velocity (U) was estimated from measured flow and cross‐sectional area derived from the flow probe diameter (Hollander et al. 2001; Penny et al. 2008). Proximal circumflex coronary blood pressure (at the location of flow measurement) was assumed to be identical to ascending aortic blood pressure (Pijls et al. 2000; Brosh et al. 2002), aside from a small time delay determined by aligning the early systolic upstroke of pressure and coronary flow. Blood density (ρ) was assumed to be 1.05 g cm⁻³. Wave speed (c) was calculated via the PU‐loop method for the aorta (Khir et al. 2001) and via the sum of squares method for the circumflex coronary artery (Davies et al. 2006b).

Coronary vascular resistance was calculated as [mean aortic pressure – mean left atrial pressure]/mean circumflex artery (Cx) flow. To define the association between the coronary BDW_dia and myocardial relaxation, the peak negative rate of change of LV pressure (LV dP/dt _min) and the time constant of relaxation (τ) were calculated (Mirsky, 1984). The latter was obtained by fitting the equation LVP = a ₁ exp[−(t − t ₀)/τ] + a ₀ to LV pressure (LVP), where a ₀ and a ₁ are fit coefficients, t ₀ is the time of dP/dt _min and the fit was performed between t ₀ and the time at which pressure had dropped to a value of P _min + 0.1(P _dpdtmin − P _min), where P _min and P _dpdtmin are the minimum diastolic pressure and the pressure at dP/dt _min.

Statistical analysis

Statistical analysis of the experimental data was performed with the MATLAB and Statistics Toolbox 2016a (The MathWorks, Inc., Natick, MA, USA). Data were tested for normality using the Lilliefors test and logarithmically transformed when non‐normal. When comparing wave magnitude between aortic and coronary arterial sites, wave intensities were normalized to the peak intensity of the FCW_sys in the respective site. Comparisons were performed with repeated measures one‐way analysis of variance. Simple and stepwise multiple linear regression with pooled data was used to test for correlations between BDW_dia magnitude and (i) LV dP/dt_min, (ii) LV τ and (iii) aortic FDW_dia. Strength of correlation is reported as adjusted R ² and interpreted as strong (0.5 < R ² ≤ 1), moderate (0.3 < R ² ≤ 0.5), weak (0.1 < R ² ≤ 0.3) or very weak (R ² ≤ 0.1). Data are reported as mean ± standard deviation, with significance defined as P < 0.05.

Results

Model‐derived data

Simulated pressure, flow and wave intensity signals in the aorta and coronary artery of the virtual older adult human are shown in Fig. 5. The coronary wave intensity profile contains all of the waves commonly identified in clinical studies, and the relative timing and magnitude of the respective waves is representative of published clinical data (Davies et al. 2006a). Importantly, the coronary FDW_dia is almost half the size of the aortic FDW_dia, relative to the FCW_sys, whereas a prominent coronary FCW_dia is present despite a negligibly small aortic FCW_dia.

Figure 5. Pressure (P), flow (Q) and wave intensity from the aorta and proximal left anterior descending artery (LAD) of the computational model.

Decompression waves are shaded.

Figure 6 shows the effects of preventing all aortic waves from passing into the coronary arteries. This abolished both the coronary FCW_sys and BCW_sys, indicating that the BCW_sys arises solely from reflection of the FCW_sys. The FDW_dia was also abolished as expected, but not the FCW_dia, with the remaining wave (designated FCW_ref) clearly arising from negative reflection of the BDW_mr, just as the FDW_ic arises from negative reflection of the BCW_ic. The remaining BDW_mr peak was 69% smaller than the BDW_dia, consistent with a contribution of wave reflection to the BDW_dia (keeping in mind that the reflected wave adds non‐linearly to BDW_mr).

Figure 6. Results of a virtual experiment in which all aortic waves were prevented from passing into the coronary arteries.

 

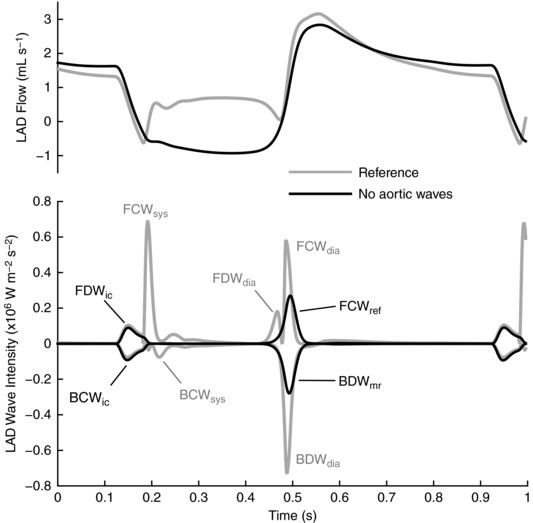
Figure 7 shows wave intensity profiles in a series of simulations in which a variable time delay (t _d) was applied to waves entering the coronary arteries from the aorta, where t _d = 0 corresponds to the reference simulation (noting that only the late systolic and early‐to‐mid diastolic periods are shown); Fig. 8 shows the corresponding peak intensity and cumulative intensity of observed waves versus t _d. With a large negative or positive delay, an ensemble of three waves related to changes in aortic pressure are seen, namely the FDW_A→C, which is reflected as a BDW_ref, then re‐reflected as a forward compression wave, referred to as FCW_ref1. This wave ensemble shifts with changing t _d, whereas the two waves arising distally from myocardial relaxation are fixed (BDW_mr and its reflected wave, FCW_ref2). Importantly, when −20 ≤ t _d ≤ 30 ms, the BDW_ref and BDW_mr overlap and only a single combined wave (BDW_dia) is apparent, which is substantially larger (peak intensity 0.76 × 10⁶ W m⁻² s⁻²) than the sum of the BDW_ref and BDW_mr waves in isolation (0.44 × 10⁶ W m⁻² s⁻²). Similarly, when the FCW_ref1 and FCW_ref2 overlap, the combined single wave (FCW_dia) is larger (0.74 × 10⁶ W m⁻² s⁻²) than the sum of the two component waves in isolation (0.31 × 10⁶ W m⁻² s⁻²). Finally, a cancelling effect of FCW_ref2 on FDW_A→C led to a resultant FDW_dia that was up to 97% smaller than the FDW_A→C. However, even when this cancellation was maximal (at t _d = 30 ms), a prominent contribution of BDW_ref remained (black arrow in Fig. 7).

Figure 7. Results of a virtual experiment in which coronary ostial pressure was shifted with a variable time delay (t _d), revealing the mechanistically distinct waves that combine (i.e. add or subtract) non‐linearly when aligned (selected time points are displayed from 23 simulations).

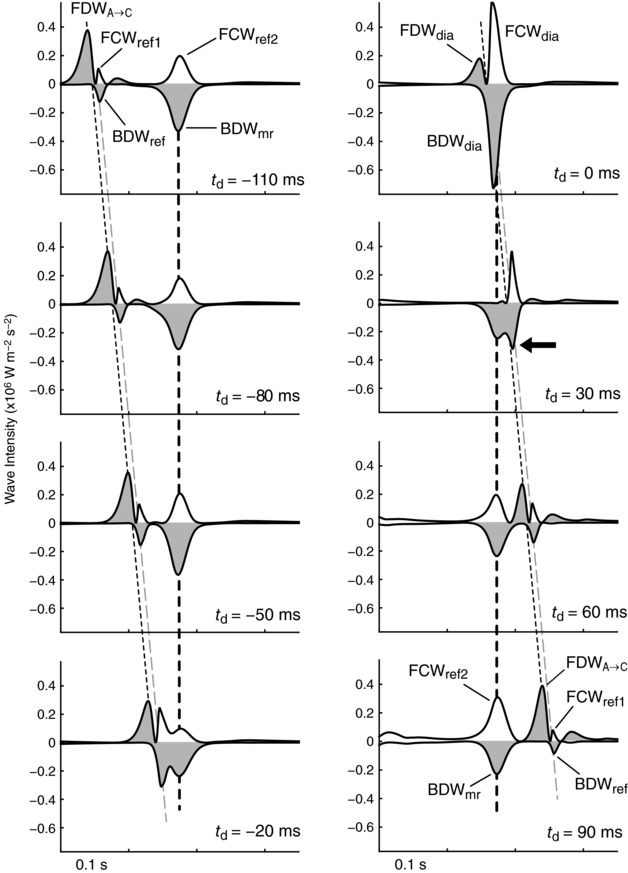
The initial ensemble of three waves seen when t _d ≤ −50 ms arise from the passage of a forward decompression wave from the aorta into the coronary arteries (FDW_A→C), and its distal reflection (BDW_ref) and proximal re‐reflection (FCW_ref1). The BDW_mr arises from a distal suction effect and is then reflected proximally (FCW_ref2). The reference case shown in Fig. 5 corresponds to t _d = 0. Dashed lines indicate the times of peak FDW_A→C (thin black line), BDW_ref (grey line) and BDW_mr (thick black line). Decompression waves are shaded.

Figure 8. Peak intensity and cumulative intensity of forward and backward waves shown in Fig. 7 versus the delay time (t _d).

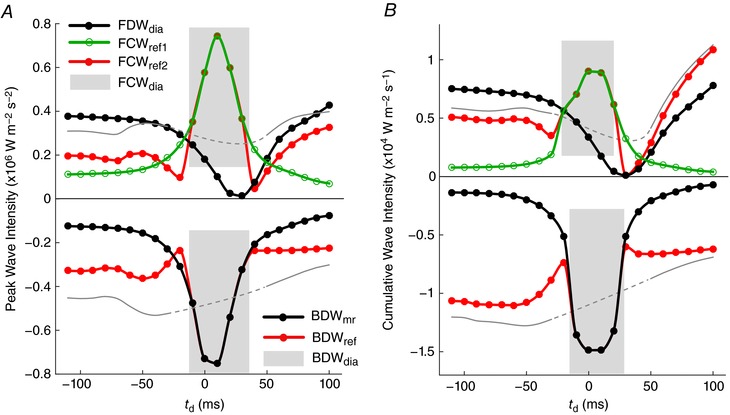
Shaded areas indicated where two waves overlap and appear as a single wave peak. Thin grey lines indicate the linear sum FCW_ref1 + FCW_ref2 (top) or BDW_mr + BDW_ref (bottom), while the dashed segments indicate an approximate interpolation; these may be compared with the observed wave magnitude, which results from non‐linear summation. Note that FDW_A→C in Fig. 7 refers to FDW_dia in the absence of interactions with reflected waves. [Color figure can be viewed at wileyonlinelibrary.com]

Based on the simulations in Fig. 7, BDW_mr accounted for 74% of the BDW_dia (peak intensity), which was similar to the value of 80% estimated from the reference simulation (t _d = 0) via eqn (7); the contribution of wave reflection was thus underestimated by 6%. Figure 9 A shows that coronary reflection index was higher during systole than diastole (difference of 0.08), as expected given the higher coronary impedance during systole. However, this value was almost identical during the early systolic and early diastolic periods in the proximal LAD (0.21 and 0.22 respectively, see shaded bars in Fig. 9 A). Further analysis revealed that the time variation of proximal LAD reflection index was similar to the resistance variation of resistance arteries (R ₁) in the intramyocardial circulation (Fig. 9 B, showing data for the terminal LAD segment, where R ₁ is the parallel sum from the three transmural layers, cf. Fig. 4 C). Combining data from all terminal arteries supplying the LV free wall and septum, R ₁ was 12 ± 3% higher (P < 0.001) during the early diastolic period (‘dia’) than early systolic (‘sys’) period (Fig. 9 C), leading to a 9 ± 8% higher reflection index during early diastole (P < 0.001, Fig. 9 D).

Figure 9. Assessment of the variation in model‐based reflection index over the cardiac cycle, obtained by setting the intramyocardial pressure source (p _im in Fig. 4 C) to zero but retaining the p _im‐related changes in intramyocardial resistance (R ₁, R _m, R ₂ in Fig. 4 C).

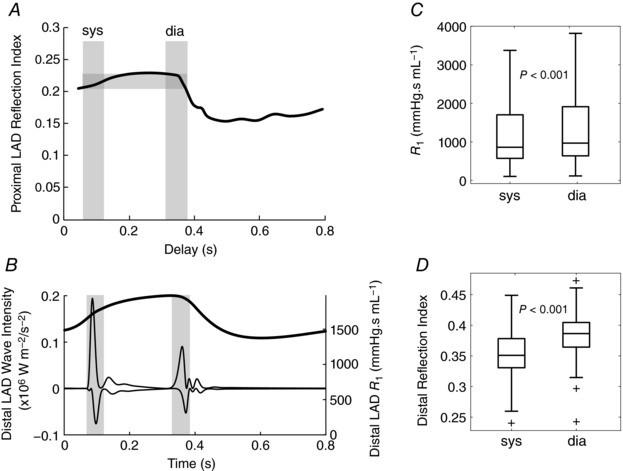
A, reflection index calculated from BCW_sys/FCW_sys cumulative intensity ratio in the proximal left anterior descending artery (LAD), with intra‐cycle variations obtained by introducing delays in coronary ostial pressure and hence the timing of incident waves (delay time based on peak BCW_sys). Grey bars indicate the early systolic period (sys) and early diastolic period (dia), which span from the start of the incident wave to the end of the reflected wave. B, wave intensity at the end of the terminal LAD segment and time‐varying R ₁ (parallel combination from all layers) in the connecting 0D microcirculation compartment. C and D, time‐averaged R ₁ during the ‘sys’ and ‘dia’ periods (C), and reflection index calculated from the local incident and reflected waves (D), obtained from all terminal 1D segments supplying the left ventricular free wall and septum.

As shown in Fig. 10, the contribution of myocardial relaxation to BCW_dia displayed minor sensitivity to changes in aortic mean pressure, intramyocardial compliance, coronary wave speed and monitoring location along the LAD; moderate sensitivity to aortic pulse pressure; and high sensitivity to intramyocardial resistance (R ₁). Overall, estimation of this contribution via eqn (7) was 6 ± 5% higher than the actual contribution obtained via the wave shifting approach. These results support the applicability of eqn (7) and suggest that small differences in reflection index between early systole and early diastole are likely to cause minor overestimation and underestimation of the contributions of myocardial relaxation and wave reflection respectively.

Figure 10. Model sensitivity analysis of key variables to the percentage contribution of myocardial relaxation to the BCW_dia .

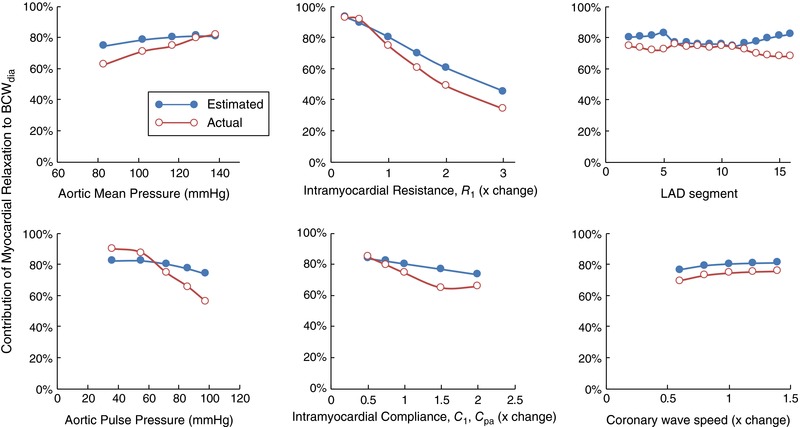
Aortic mean and pulse pressures were adjusted by varying systemic vascular resistance and aortic wave speed respectively. Intramyocardial resistance (R ₁) and compliances (C ₁ and C _pa) are indicated in Fig. 4 C. ‘LAD segment’ refers to the 1D segment numbers shown in Fig. 4 A. ‘Estimated’ refers to values estimated via eqn (7) and ‘actual’ refers to values obtained by shifting ostial pressure by −60 ms, which separates the BDW_mr and BDW_ref (cf. Fig. 7). [Color figure can be viewed at wileyonlinelibrary.com]

The difference between true coronary FDW_A→C (based on simulations in Fig. 7) and that estimated from eqn (4) (when t _d = 0) was less than 5%. True coronary FCW_A→C could not be ascertained for comparison with eqn (5) due to re‐reflection of the BDW_ref at the coronary ostium.

In vivo data

Haemodynamics

A summary of relevant haemodynamic data is provided in Table 1. Heart rate and cardiac output decreased after l‐NNA (P < 0.05) but did not change with aortic constriction. Systolic blood pressure increased by a similar amount with l‐NNA and aortic constriction (P = 0.13) but was related to an increase in mean pressure in the former and pulse pressure in the latter. Cx flow was similar in both groups at baseline (P = 0.7) but increased more with aortic constriction than l‐NNA (by 26.5 ± 9.8 vs. 13.7 ± 12.3 mL min⁻¹, P = 0.03) despite a higher diastolic pressure with l‐NNA (P = 0.03, Table 1). Coronary vascular resistance increased by ∼30% after l‐NNA (P = 0.04) but did not change with aortic constriction (P = 0.28). LV dP/dt _min and τ were similar in both groups at baseline (P > 0.5) and displayed similar (P > 0.3) changes with afterload increase.

Table 1.

Haemodynamic data for the in vivo experiments

	l‐NNA group (n = 11)		Constriction group (n = 7)
	Baseline	l‐NNA	Baseline	Aortic constriction
Heart rate (bpm)	110 ± 14	100 ± 14a	105 ± 17	111 ± 17
Cardiac output (L min−1)	3.12 ± 0.68	2.56 ± 0.44a	3.07 ± 0.65	3.67 ± 0.88
Cx flow (mL min−1)	29.5 ± 11.6	43.2 ± 17.7b	32.1 ± 16.1	58.6 ± 19.9c
Cx effective vascular resistance (mmHg.min mL−1)	2.44 ± 1.18	3.13 ± 1.60a	2.37 ± 0.99	2.13 ± 0.80
Ao systolic BP (mmHg)	75.5 ± 7.7	134.5 ± 11.9c	79.5 ± 7.6	147.4 ± 7.6c
Ao mean BP (mmHg)	66.3 ± 9.1	123.9 ± 11.2c	70.5 ± 9.2	121.8 ± 8.8c
Ao diastolic BP (mmHg)	58.1 ± 10.0	115.5 ± 10.6c	62.4 ± 10.5	103.0 ± 11.4c
Ao pulse BP (mmHg)	17.4 ± 3.9	19.0 ± 2.6	17.0 ± 4.3	44.3 ± 9.9c
LV dP/dtmin (mmHg s−1)	−1195 ± 191	−1878 ± 370c	−1271 ±294	−2126 ± 443c
LV τ (ms)	27.8 ± 4.7	19.3 ± 4.6c	29.1 ± 5.9	21.5 ± 8.7a

Ao, aortic; BP, blood pressure; Cx, circumflex coronary artery; dP/dt_min, maximal rate of pressure fall; LV, left ventricular; τ, time constant of isovolumic relaxation.

^a P < 0.05, ^b P ≤ 0.01, ^c P < 0.001 compared with baseline.

Baseline variables between l‐NNA and aortic constriction groups were not significantly different.

Systolic waves

Wave intensity data are summarized in Table 2 and a representative example is shown in Fig. 11. Results are here discussed in relation to peak intensity unless otherwise stated, but similar findings pertain to cumulative intensity (Table 3). Aortic (Ao) and Cx FCW_sys decreased substantially with l‐NNA (P < 0.004) but did not change with aortic constriction (P = 0.7). The concept that Cx BCW_sys arises from reflection of the Cx FCW_sys was supported by a strong correlation between these waves (R ² = 0.62; P < 0.001), along with a relatively consistent delay of 23.9 ± 6.6 ms that did not change with increased afterload (P > 0.4). Moreover, the reflection index Cx BCW_sys/FCW_sys (0.26 ± 0.20 at baseline) more than doubled after l‐NNA infusion (P < 0.001), but was unaffected by aortic constriction (P = 0.8).

Table 2.

Peak wave intensity for the in vivo study

	Baseline	l‐NNA	Baseline	Aortic constriction
Systolic waves
Ao FCWsys	81.8 ± 55.9	19.1 ± 4.5b	86.5 ± 56.7	95.6 ± 43.7
Cx FCWsys	14.6 ± 8.0	2.0 ± 1.1c	18.6 ± 11.1	20.7 ± 13.6
Cx BCWsys	−3.1 ± 2.2	−1.1 ± 0.4b	−6.0 ± 5.1	−6.6 ± 5.8
Cx | BCWsys/FCWsys |	0.21 ± 0.08	0.64 ± 0.31c	0.35 ± 0.30	0.32 ± 0.14
Diastolic waves
Ao FDWdia	74.3 ± 18.3	106.6 ± 30.9c	86.8 ± 25.9	152.6 ± 81.2a
Ao FCWdia	21.9 ± 14.1	28.0 ± 16.8	30.2 ± 29.6	27.7 ± 51.4
Cx FDWdia	6.0 ± 3.0	5.3 ± 2.6	5.5 ± 2.3	9.2 ± 4.8
Cx FDWA → C (eqn 4)	14.9 ± 6.4	10.5 ± 5.5	17.9 ± 5.3	31.9 ± 22.2
Cx FCWdia	13.1 ± 5.7	16.0 ± 10.3	18.7 ± 13.5	15.8 ± 12.7
Cx FCWA → C (eqn 5)	3.9 ± 2.2	3.0 ± 2.6	6.7 ± 7.1	4.0 ± 5.4
Cx BDWdia	−8.5 ± 6.2	−10.3 ± 5.5	−13.2 ± 7.7	−22.8 ± 17.1
Cx BDWref (eqn 6)	−3.2 ± 1.9	−5.7 ± 1.9 b	−5.5 ± 4.1	−9.7 ± 7.5
Cx BDWmr (eqn 7)	−2.2 ± 3.3	−1.1 ± 1.4	−2.5 ± 2.7	−3.2 ± 2.6
Cx BDWmr /(BDWmr + BDWref)	30 ± 34%	13%± 16%	31 ± 27%	24 ± 21%

Time‐corrected wave intensity units: 10⁴ W m⁻² s⁻².

^a P < 0.05, ^b P ≤ 0.01, ^c P < 0.001 compared with the respective baseline.

Items in italics refer to component waves that were estimated via the indicated equation. There were no significant differences between baselines of l‐NNA and aortic constriction groups for any quantity.

Figure 11. Representative example of simultaneously acquired wave intensity in the sheep aortic trunk (left) and circumflex coronary artery (right) in relation to blood pressure (P) and flow (Q) waveforms.

High‐fidelity pressure was measured in the aortic trunk and was assumed to be the same as circumflex coronary pressure (aside from a time offset applied to align early‐systolic pressure and flow upstrokes). Wave abbreviations: BCW, backward compression wave; BDW, backward decompression wave; FCW, forward compression wave; FDW, forward decompression wave. Decompression waves are shaded. The main waves occur during early systole (‘sys’) and early diastole (‘dia’).

Table 3.

Cumulative wave intensity (i.e. area under the wave)

	Baseline	l‐NNA	Baseline	Aortic constriction
Systolic waves
Ao FCWsys	22.46 ± 12.86	9.81 ± 3.10b	24.93 ± 14.14	27.44 ± 9.02
Cx FCWsys	2.83 ± 1.61	0.86 ± 0.40b	3.80 ± 2.08	4.23 ± 3.25
Cx BCWsys	−0.81 ± 0.56	−0.53 ± 0.28	−1.42 ± 1.11	−1.47 ± 1.11
Cx | BCWsys/FCWsys |	0.29 ± 0.11	0.61 ± 0.20c	0.39 ± 0.26	0.39 ± 0.20
Diastolic waves
Ao FDWdia	14.38 ± 3.52	18.57 ± 4.33b	16.86 ± 3.38	31.72 ± 11.27b
Ao FCWdia	2.42 ± 1.51	2.69 ± 1.65	3.62 ± 3.41	2.36 ± 4.64
Cx FDWdia	1.00 ± 0.51	0.70 ± 0.31a	0.92 ± 0.48	1.72 ± 1.16
Cx FDWA → C (eqn 4)	1.93 ± 0.85	1.60 ± 0.56 a	2.62 ± 1.30	4.68 ± 2.72
Cx FCWdia	1.62 ± 0.68	1.77 ± 1.11	2.32 ± 1.84	1.62 ± 1.38
Cx FCWA → C (eqn 5)	0.30 ± 0.17	0.22 ± 0.17	0.64 ± 0.79	0.24 ± 0.37
Cx BDWdia	−1.95 ± 0.83	−2.10 ± 0.87	−2.60 ± 1.15	−4.80 ± 2.42a
Cx BDWref (eqn 6)	−0.57 ± 0.32	−0.95 ± 0.34 a	−0.87 ± 0.51	−1.63 ± 1.16

Cumulative wave intensity units: 10³ W m⁻² s⁻¹.

^a P < 0.05, ^b P ≤ 0.01, ^c P < 0.001 compared with the respective baseline.

Items in italics refer to component waves that were estimated via the indicated equation. There were no significant differences between baseline of Group 1 and baseline of Group 2 for any quantity. Note that BDW_mr cumulative intensity cannot be calculated as for peak intensity.

Diastolic waves

Large differences in the relative intensity of early‐diastolic forward waves were found when comparing Ao and Cx sites (Fig. 12). After normalization to FCW_sys, Cx FDW_dia was smaller than Ao FDW_dia in every recording (by 40 ± 16% overall), whereas Cx FCW_dia was always much larger than Ao FCW_dia (by 512 ± 373%).

Figure 12. Comparison of early diastolic forward wave magnitude in the ascending aorta vs. the circumflex coronary artery at (A) baseline (all animals, n = 18), (B) after aortic constriction (n = 7) and (C) after administration of l‐NNA (n = 11, note the difference in y‐axis scale).

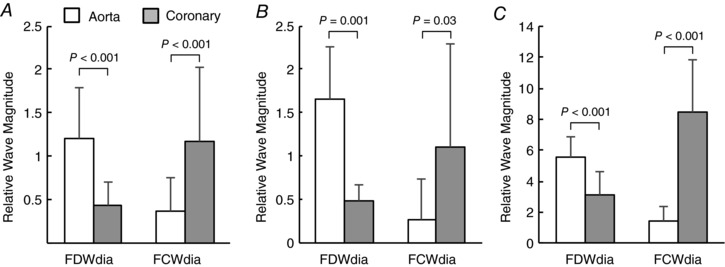
Peak wave intensities of FDW_dia and FCW_dia are expressed relative to that of FCW_sys in the respective measurement location.

The estimated Cx BDW_ref almost doubled with l‐NNA (P = 0.007) but did not increase significantly with aortic constriction (P = 0.12). Cx BDW_mr accounted for only ∼30% of the measured BDW_dia at baseline (eqn 8), with a trend for this contribution to decrease after LNNA (to 13%, P = 0.09, Table 2).

With simple linear regression, no correlation was detected between Cx BDW_dia and LV τ (R ² < 0.1, P > 0.05, Fig. 13, left panels), but a weak‐to‐moderate correlation was found between normalized Cx BDW_dia magnitude and LV dP/dt_min (R ² = 0.3, P ≤ 0.001, Fig. 13, middle panels). Conversely, a strong correlation was found between Cx BDW_dia and Ao FDW_dia (R ² > 0.6, P < 10⁻⁷, Fig. 13, right panels). Upon multiple linear regression analysis, LV dP/dt_min did not provide additional predictive value over Ao FDW_dia (P = 0.4), again suggesting that reflection of FDW_A→C made a greater contributor to BDW_dia than distal suction effects.

Figure 13. Linear regression analyses investigating relationships between the circumflex coronary (Cx) BDW_dia and LV isovolumic time constant (τ), LV dP/dt _min and aortic (Ao) FDW_dia, with wave magnitude quantified via peak wave intensity (top panels) and cumulative intensity (bottom panels) normalized to the respective FCW_sys .

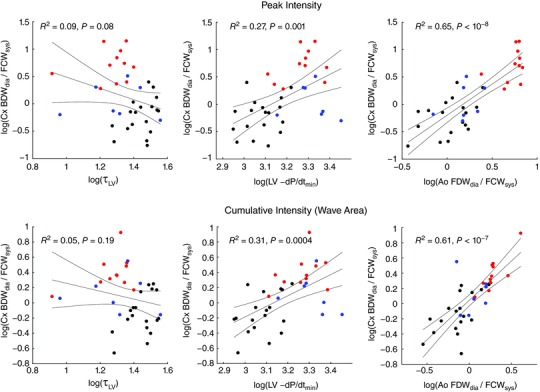
Data point colours (online version only) refer to baseline (black, both groups), l‐NNA infusion (red) and aortic constriction (blue). [Color figure can be viewed at wileyonlinelibrary.com]

Discussion

A skilled magician uses smoke and mirrors to conceal, exaggerate and mislead. This study uncovered a phenomenon whereby coronary wave reflection acts in a similar way, obscuring the true influence of active upstream and downstream forces on early diastolic waves in conduit arteries. Specifically, although distal myocardial relaxation generates a backward‐running decompression (or ‘suction’) wave, as is currently believed (Davies et al. 2006a), distal reflection of a forward decompression wave can have a major ‘exaggerating’ effect on the measured backward wave (BDW_dia), due to a non‐linear wave addition phenomenon. Moreover, near‐complete negative reflection of the BDW_dia at the coronary ostium produces a forward compression wave (FCW_ref) that conceals the aortic FDW_dia and exaggerates the aortic FCW_dia when viewed from the coronary arteries.

While an oft‐stated benefit of coronary wave intensity is that it allows clear assessment of upstream and downstream processes (Siebes et al. 2009; Lu et al. 2011; Kyriacou et al. 2012; Rolandi et al. 2012; Claridge et al. 2015; Lee et al. 2016; Raphael et al. 2016), a key conclusion of this study is that, mechanistically, both upstream and downstream processes can have a significant effect on the magnitude of both forward and backward waves (directly and via wave reflection). However, with additional knowledge of aortic wave intensity, we have described a novel method to unmask the effect of wave reflection and recover information about upstream and downstream forces (such as distal suction) on early‐diastolic coronary waves.

Wave reflection in coronary arteries

Limited information exists about wave reflection in coronary arteries. Rumberger et al. (1979) posited wave reflection as an explanation for prominent pressure and velocity oscillations observed in distal coronary arteries of the horse, while Arts et al. (1979) concluded that, in dogs, frequencies below 7 Hz are reflected at the coronary peripheral resistance, whereas higher frequencies undergo minimal reflection. The study by Arts et al. (1979), and in particular a recent detailed morphometric and theoretical study by Rivolo et al. (2016), suggested that the major conduit coronary arteries are relatively well matched in the forward direction, as was assumed in the design of our 1D model. This implies that wave reflection occurs mainly in the small resistance arteries.

Davies et al. (2006a) proposed reflection of FCW_sys as a likely mechanism underlying the BCW_sys. This was supported by our modelling study, in which blocking the aortic FCW_sys from passing into the coronary arteries abolished the BCW_sys (Fig. 6). Further support for this interpretation was provided by experimental data showing a strong correlation between BCW_sys and FCW_sys, a consistent delay between these waves and a wave intensity‐based reflection index that increased dramatically with coronary vasoconstriction.

Along with distal reflection, Davies et al. (2006a) also proposed that backward‐running waves arriving at the coronary ostium are likely to undergo near‐complete negative reflection, due to the large impedance decrease at this junction. Hence, during isovolumic contraction, an FDW_ic was postulated to arise from negative reflection of the BCW_ic; this explanation was supported by our virtual experiments in which preventing aortic waves from passing into the coronary arteries did not affect FDW_ic (Fig. 6).

In contrast to its recognized major influence during early systole, however, the potential role of wave reflection in modulating the coronary wave intensity profile during early diastole has largely been ignored until the present study.

Early‐diastolic backward decompression wave (BDW_dia)

The BDW_dia is considered the most important coronary wave physiologically, as it appears to be the primary actuator of diastolic coronary blood flow and is influenced by factors such as ageing, exercise, aortic stenosis, LV hypertrophy, coronary stenosis and myocardial resynchronization therapy (Davies et al. 2006a; Kyriacou et al. 2012; Lockie et al. 2012; De Silva et al. 2013; Claridge et al. 2015; Narayan et al. 2015). The BDW_dia is currently interpreted as arising solely from a suction effect within the coronary microcirculation, as the relaxing myocardium releases the external (intramyocardial) pressure developed during systole (Davies et al. 2006a; Kyriacou et al. 2012; Narayan et al. 2015). Lee et al. (2016) investigated the sensitivity of the major coronary waves to several key parameters in their model and found a dependence of BDW_dia on myocardial relaxation rate and degree of dysynchrony, consistent with the distal suction mechanism; however, a possible contribution of wave reflection was not explored.

Our experimental and computational data provide strong evidence that wave reflection makes an important contribution to the BDW_dia. In the computational model, preventing aortic waves from passing into the coronary arteries caused BDW_dia amplitude to fall by 69%, suggesting a contribution of reflection to this wave. In the experimental data, a strong correlation was found between the size of the incident wave (FDW_A→C) and BDW_dia (R ² > 0.6), but there was no correlation with LV τ and only a weak‐to‐moderate correlation with LV dP/dt _min (R ² = 0.3) that lost significance in a multivariate model. Previous studies have reported R ² values of 0.21−0.35 between LV dP/dt _min and the coronary BDW_dia, in agreement with our findings (Kyriacou et al. 2012; Ladwiniec et al. 2016), although Ladwiniec and colleagues also reported a correlation (R ² = 0.35) between LV τ and BDW_dia (Ladwiniec et al. 2016).

A surprising finding of our study was that the distal suction mechanism (i.e. BDW_mr) accounted for only 30% of the measured BDW_dia in the experimental study, and hence wave reflection appeared to be the dominant mechanism. Moreover, coronary vasoconstriction with l‐NNA increased the reflection‐related wave (BDW_ref) and tended to reduce the contribution of distal suction (see Table 2). However, these data in healthy, young sheep contrasted with the computational model representing an older, hypertensive human in which the distal suction mechanism was dominant, accounting for ∼75% of the BDW_dia. The contribution of distal suction to BDW_dia may therefore be quite variable and influenced by a variety of (patho)physiological factors; these should be investigated in more detail in future studies.

We showed for the first time that, due to the definition of wave intensity as dPdU, the addition of two mechanistically distinct waves is non‐linear. In other words, when BDW_ref and BDW_mr combine, the resultant wave (BDW_dia) is substantially greater than simply BDW_ref + BDW_mr (by ∼60% at baseline in our sheep studies). This may partly explain why the BDW_dia is so prominent in many published figures, much more so than the BCW_ic despite in vivo data suggesting that intramyocardial pressure rises (during isovolumic contraction) and falls (during isovolumic relaxation) at a similar rate (Rabbany et al. 1989). An important implication of this non‐linear addition principle is that any delay between BDW_ref and BDW_mr may substantially influence the intensity of the combined or partially combined wave (e.g. compare t _d = −20 ms and t _d = 0 ms in Fig. 7). That the BDW_ref and BDW_mr may not always be aligned is suggested by numerous published figures in which multiple BDW peaks are evident in the early diastolic period, although this could also be due to other factors such as dyssynchronous relaxation (Hadjiloizou et al. 2008; Davies et al. 2011; Kyriacou et al. 2012; Lu et al. 2012; De Silva et al. 2014; Broyd et al. 2016; Raphael et al. 2016).

Early‐diastolic forward decompression wave (FDW_dia)

Based on the seminal work of Parker et al. (1988), the FDW_dia is widely regarded as the second major wave in the aortic wave intensity profile and is associated with a fall in pressure and flow prior to valve closure. An FDW_dia also appears in the coronary wave intensity profile and is believed to arise from transmission of the aortic FDW_dia into the coronary arteries (Davies et al. 2006a). However, we found that the coronary FDW_dia was ∼60% smaller (peak intensity, after normalization to FCW_sys) than the aortic FDW_dia. Closer inspection revealed that the FDW entering the coronary arteries from the aorta (FDW_A→C) is partially cancelled by negative reflection of the BDW_dia at the coronary ostium (see Fig. 3 B). Such reflection produces a forward compression wave (FCW_ref) which has a cancelling/concealing effect on the FDW_A→C.

Introduction of a variable delay between aortic‐originating waves and distally generated waves in a virtual experiment indicated that this cancelling effect can cause the FDW_A→C to essentially disappear under certain circumstances (Fig. 7). It is tempting to conclude that if the measured coronary FDW_dia is small or even absent, wave reflection must make a negligible contribution to the BDW_dia. However, we found that a prominent BDW_ref may still be present in such circumstances, apparently because the BDW_ref arises from reflection of the concealed FDW_A→C (see t _d = 30 ms in Fig. 7). For this reason, the true influence of wave reflection on the BDW_dia should be assessed with respect to FDW_A→C as the incident wave, rather than FDW_dia.

Diastolic forward compression wave (FCW_dia)

An aortic FCW_dia arises from the transitory increase in pressure and flow associated with the dicrotic notch as the valve closes. This wave is also commonly observed in the coronary arterial wave intensity profile (Davies et al. 2006a; Hadjiloizou et al. 2008; Kyriacou et al. 2012; Lu et al. 2012; Ladwiniec et al. 2016; Raphael et al. 2016) and has been interpreted to arise from transmission of the aortic FCW_dia into the coronary arteries (Davies et al. 2006a; Narayan et al. 2015). However, inspection of published figures from these two locations suggest that the FCW_dia is generally more prominent in coronary arteries (Davies et al. 2006a; Kyriacou et al. 2012; Lu et al. 2012; Sinclair et al. 2015; Raphael et al. 2016) than in the aorta (Parker & Jones, 1990; Jones et al. 2002; Khir & Parker, 2005; Penny et al. 2008; Lu et al. 2012). Consistent with this impression, our comparison of concurrent aortic and coronary wave intensity profiles indicated that the coronary FCW_dia peak intensity was 2–21 times higher than aortic FCW_dia, relative to FCW_sys (see Fig. 12); in the computational studies, aortic FCW_dia was of negligible size but the coronary FCW_dia was very prominent (see Fig. 5).

The combination of experimental and computational data suggested that two mechanisms contributed to the FCW_dia. As expected, the first was transmission of the aortic FCW_dia into coronary arteries. However, the second and perhaps dominant mechanism was negative reflection of the BDW_dia at the coronary ostium (FCW_ref), which was clearly demonstrated with a virtual experiment in which aortic waves were prevented from passing into the coronary arteries (see Fig. 6).

Overcoming the smoke and mirrors effect

A major conclusion of this study is that wave reflection obscures the true (i.e. wave reflection‐independent) influence of upstream and downstream forces on the early diastolic forward and backward waves. However, by making use of information from concurrent aortic wave intensity, we proposed novel techniques for estimating the reflection‐independent waves that pass from the aorta into the coronary arteries (FDW_A→C and FCW_A→C) and arise from distal suction effects (BCW_mr), as well as the reflection‐related contribution to BDW_dia (i.e. BDW_ref). In silico validation with our model suggested that these waves can be estimated with errors of less than 10%.

The proposed wave estimation techniques depend on several assumptions being satisfied. The first is that aorto‐coronary wave transmission does not vary significantly between early systole and early diastole; indeed, based on transmission line theory, we calculated differences in transmission coefficient of less than 5% (Mynard et al. 2017). The second assumption (required for estimation of BDW_ref and BCW_mr) is that the coronary reflection coefficient is similar during early systole and early diastole (when FCW_sys and FDW_dia occur). When we tested this assumption using our model, we found that model‐predicted reflection index was comparable to that in the experimental studies (0.21 vs. 0.29) and changed by less than 0.01 between early systole and early diastole (Fig. 9 A). Model data also suggested that both intramyocardial resistance and distal reflection index were ∼10% higher during early diastole than early systole (Fig. 9 B–D), which, if anything, would tend to cause the contribution of wave reflection on BDW_dia to be underestimated.

Study limitations

This study had a number of limitations. Experimental studies were performed in healthy, young, anaesthetized open‐chest sheep undergoing mechanical ventilation, and thus caution should be applied in extrapolating results to humans and other species with or without pathophysiology undergoing spontaneous respiration. While previous studies suggest that the anaesthetic alpha‐chloralose has (Covert et al. 1989) or does not have (Cox, 1972) a vasoconstrictive effect, systemic vascular resistance at baseline in this study (21.9 ± 4.4 mmHg.L min⁻¹) was only slightly higher than the range 18.8–21.2 mmHg.L min⁻¹ in chronically instrumented conscious sheep (Kemp et al. 1995) and effective circumflex coronary resistance in this study (2.4 ± 1.1 mmHg.min mL⁻¹) was the same as that derived from data in conscious sheep (Bednarik & May, 1995; Parkes et al. 1997). However, we cannot exclude the possibility that some coronary vasoconstriction could have led to a greater influence of wave reflection on the BDW_dia, although any such effect is likely to be small.

The computational model is based on findings of many physiological studies from other research groups (Fisher et al. 1982; Spaan, 1985; Bruinsma et al. 1988; Rabbany et al. 1989; Dodge et al. 1992; Spaan et al. 2000; Algranati et al. 2010), has been validated in sheep (Mynard et al. 2014) and produced wave intensity profiles that were very consistent with published in vivo waveforms (Davies et al. 2006a). However, a number of factors were not accounted for in the model, such as the effects of cardiac motion (Ramaswamy et al. 2004), wave propagation effects in the microcirculation (Guiot et al. 1990) and the effects of external constraint on conduit arteries (Liu et al. 2008). The coronary microcirculation was modelled using lumped elements and simplifying assumptions were made about intramyocardial pressure. More detailed microvascular models, such as the poromechanical model described by Lee et al. (2016), may be useful for further investigating some of the issues raised in this paper.

While this study highlighted the complexity of coronary arterial wave dynamics, we did not study the effect of multiple re‐reflections. In the sheep under baseline conditions, the magnitude of second‐ and third‐generation waves would be expected to be in the order of ∼6% and ∼1.5% that of initial incident wave, not accounting for wave dispersion and dissipation. However, in cases where wave reflection is high (e.g. vasoconstriction or stenosis), these re‐reflections may be more influential. Use of the theoretical framework described in this paper could be used in future to investigate these wave dynamics in even greater detail, although the limited fidelity of experimental data may make this challenging. We also did not investigate issues related to the ‘windkesselness’ of the coronary arterial network, which can lead to errors when calculating wave speed and separating wave intensity into forward and backward components (Kolyva et al. 2008; Siebes et al. 2009).

Conclusions

This study revealed a ‘smoke and mirrors’ effect caused by wave reflection that obscures the true upstream and downstream contributions to early diastolic coronary waves. Experimental and computational data supported our hypothesis that the FDW_dia, FCW_dia and BDW_dia are all affected by wave reflection and, hence, both upstream and downstream forces. In particular, the dominant BDW_dia appears to arise from a combination of distal suction and wave reflection, with non‐linear addition of the two component waves being a significant factor underlying the prominence of this wave. The FDW_dia and FCW_dia are attenuated and augmented respectively by negative reflection of the BDW_dia at the coronary ostium. These findings have significant implications for the prevailing interpretation of the coronary wave intensity profile. We also proposed techniques for recovering the waves arising from non‐reflection‐related upstream forces (for forward waves) and downstream forces (for backward waves). While the precise contribution of wave reflection and active mechanisms in humans under various conditions must be established in future studies, the principles and techniques described in this study are likely to have an important impact on the interpretation of coronary wave intensity profiles in health and disease.

Additional information

Conflicts of interest

None.

Author contributions

JPM: conception and design, computational studies, data analysis, preparation of figures and manuscript; DJP and JJS: design and conduct of laboratory experiments. All authors edited and revised the manuscript, approved the final version and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

JPM was supported by a CJ Martin Early Career Research Fellowship from the National Health and Medical Research Council of Australia. This work was supported by the Victorian Government's Operational Infrastructure Support Program.

Translational perspective

Wave intensity analysis is an emerging technique that is being used to unravel the upstream (aortic) and downstream (intramyocardial) forces that determine coronary blood flow. A dominant backward decompression wave (BDW_dia) accompanies the early‐diastolic surge in coronary flow and, based on a number of published studies, has been shown to have potential clinical value. To date, it has been widely held that the BDW_dia is generated in the coronary microvasculature via a suction effect caused by myocardial relaxation. Our study provides evidence that another mechanism contributes to the BDW_dia, namely passive wave reflection of a forward wave entering the coronary arteries from the aorta. We also show that summation of the wave reflection and myocardial relaxation forces is non‐linear, i.e. the resultant combined wave is substantially larger than the simple sum of waves from each mechanism acting in isolation. This finding may impact on the interpretation of clinical studies assessing BDW_dia magnitude under healthy or disease conditions and how it changes with intervention. With an additional measurement of ascending aortic wave intensity, the separate contributions of wave reflection and myocardial relaxation to BDW_dia may be estimated, thus providing more detailed and accurate insights into the upstream and downstream forces that determine coronary flow.

Appendix 1.

Model parameters

Cardiovascular model

Parameters for the closed‐loop cardiovascular model were taken from Mynard et al. (2012) and adjusted to represent an older adult arterial system with target haemodynamic values described in the Methods. Parameters governing the heart chambers, valves, 1D segments and vascular beds shown in Fig. 4 are given in A1, A2, A3, A4.

Table A1.

Model parameters for heart chambers

	LV	RV	LA	RA
E max (mmHg mL−1)	2.2	0.35	0.13	0.09
E min (mmHg mL−1)	0.07	0.035	0.09	0.045
V 0 (mL)	10	60	3	7
Vt  = 0 (mL)	150	155	80	60
K S (10−3 s mL−1)	1.00	1.00	0.25	0.50
τ1 (s)	0.215	0.215	0.042	0.042
τ2 (s)	0.362	0.362	0.138	0.138
m 1 (–)	1.32	1.32	1.99	1.99
m 2 (–)	21.9	21.9	11.2	11.2
κ (–)	6	6	2	2
μAV (g cm−7 s−1)	0	0	0.033	0.05
t onset (s)	0	0	0.65	0.65

E _max, maximum free wall elastance; E _min, minimum free wall elastance; V ₀, pressure‐axis intercept of the pressure–volume relation; V_{t  = 0}, initial chamber volume; K _S, source resistance coefficient; τ₁/τ₂, contraction/relaxation time constants; m ₁/m ₂, contraction/relaxation rate constants; κ, septal elastance constant (ventricular interaction via the septum); μ_AV, atrioventricular plane piston constant (atrioventricular interaction); t _onset, onset time of contraction. Note: no pericardial constraint was applied. See Mynard and Smolich (2015) for an explanation of these parameters.

Table A2.

Model parameters for heart valves

	Av	Pv	Mv	Tv	Vv
A eff,max (cm2)	4.9	5.7	5.1	6	6
A eff,min (cm2)	0.0	0.0	0.0	0.0	0.0
l eff (cm)	1.5	1.5	2	2	1.5
K vo (cm2 s2 g−1)	0.02	0.02	0.02	0.03	0.03
K vc (cm2 s2 g−1)	0.02	0.02	0.04	0.04	0.03

A _eff,max, maximum effective valve area (when fully open); A _eff,max, minimum effective valve area (when closed); l _eff, effective length; K _vo, valve opening rate coefficient; K _vc, valve closure rate coefficient. Valve abbreviations: Av, aortic valve; Pv, pulmonary valve; Mv, mitral valve; Tv, tricuspid valve; Vv, venous valve. See Mynard et al. (2012) and Mynard and Smolich (2015) for an explanation of these parameters.

Table A3.

Model parameters for one‐dimensional segments of the cardiovascular model (see Fig. 4 B)

	L (cm)	A 0 (cm2)	c 0 (cm/s)	P 0 (mmHg)
LVot	1	7.2	900	90
AoRt	1	7.2	900	90
SA	40	7.2 → 5.0	900 → 1286	90
SV1	10	6	150	4.5
SV2	5	6	150	4.5
RVot	1	7.1	250	14
PA	5	7.1 → 10.6	250	14
PV	5	10	150	8.5

L is segment length. A ₀, c ₀ and P ₀ are reference cross‐sectional area, wave speed and pressure. Abbreviations: LVot, left ventricular outflow tract; AoRt, aortic root proximal to the coronary ostia; SA, systemic artery; SV, systemic vein (two segments separated by a venous valve); RVot, right ventricular outflow tract; PA, pulmonary artery; PV, pulmonary vein. Arrows indicate linear tapering from proximal to distal values.

Table A4.

Model parameters for the vascular beds in the cardiovascular model (see Fig. 4 B)

	R 0 (mmHg.s mL−1)	C art (mL mmHg−1)	C ven (mL mmHg−1)
SVB	1.8	0.5	11
PVB	0.05	5.0	15

R ₀, reference resistance; C _art, arterial compliance; C _ven, venous compliance. Vascular bed abbreviations: SVB, systemic vascular bed; PVB, pulmonary vascular bed. Note that arterial and venous characteristic impedances (Z _0,art, Z _0,ven in Fig. 4 B) were calculated from the connecting 1D segment as ρc ₀/A ₀, where ρ = 1.06 g cm⁻³ is blood density (see A3).

One‐dimensional conduit coronary arteries

The geometry of the right‐dominant 1D coronary conduit arterial model (i.e. reference cross‐sectional area, length and connectivity of all 1D segments) was identical to that in Mynard & Smolich (2016a) and is therefore not reproduced here. The only difference was that, compared with the model in Mynard & Smolich (2016a), the wave speed of all segments was increased by 250% compared with those representing a healthy young circulation, resulting in a proximal LAD wave speed of 20.8 m s⁻¹, similar to reported values in older adult patients (Davies et al. 2006a; Rolandi et al. 2012).

Coronary microcirculation model

Terminal 1D segments perfuse parts of the LV free wall (LVfw), right ventricular free wall (RVfw) and septum (Sep). As in previous work (Mynard et al. 2014; Mynard & Smolich, 2016a), total microcirculatory resistance (i.e. R ₁ + R _m + R ₂ in Fig. 4 C) was determined iteratively to achieve a target mean flow (2.54%, 0.66% and 1.35% of cardiac output, for the LVfw, RVfw and septum respectively). This flow was distributed amongst instances of the 0D model in proportion to their myocardial weights, which in turn were distributed according to the inverse cube of penetrating artery radii (i.e. Murray's law). Total weights for the adult human LVfw, RVfw and septum of 104, 46 and 54 g respectively were taken from Lorenz et al. (1999). Subendocardial‐to‐subepicardial flow ratios (1.24 and 1.18 for LVfw and RVfw) and left‐to‐right septal flow ratios (1.37) were taken from Fisher et al. (1982). We assumed R ₁ = 1.2R _m and R ₂ = 0.5R _m in all myocardial regions and that 75% of R _m is dependent on the volume of chamber 1 and the remainder is dependent on chamber 2 (Spaan et al. 2000). Compliances were set to C ₁ = 0.013 and C ₂ = 0.254 mL mmHg⁻¹/100 g, and reference volumes V _0,1 = 2.5 and V _0,2 = 8.0 mL/100 g, both with a subendocardial‐to‐subepicardial (or left‐to‐right septal) ratio of 1.14 (Weiss & Winbury, 1974; Bruinsma et al. 1988). CEP was assumed to decline linearly from ventricular cavity pressure at the endocardium to pericardial pressure (assumed to be zero) at the epicardium, while SIP was assumed to be the same in each transmural layer, with a peak value equal to 20% of cavity pressure and a waveform shape identical to the ventricular chamber elastance curve (Mynard et al. 2014).