Fig. 3.

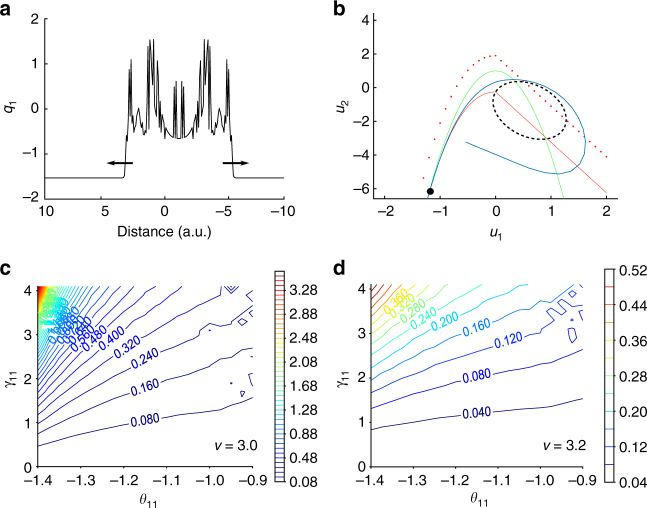
Seizure propagation via slow-traveling ictal wavefront in the Epileptor field model. a Plot of a traveling front solution in the fast population. b Phase space for the fast population variables (u₁ and u₂). In the interictal state, the system is on the left stable fixed point (black dot) at the crossing of the cubic-linear nullcline ${\stackrel{°}{u}}_1=0$ (full red line) of Eq. 1 and the squared nullcline ${\stackrel{°}{u}}_2=0$ (green line) of Eq. 2 (Methods). After seizure onset, excitation through local coupling moves the red nullcline of neighboring Epileptors upward (dashed red line) until disappearance of the left stable fixed point, resulting in the activity (blue line) to jump to the stable limit cycle (black dashed line). c Speed of propagation (a.u.) of the ictal wavefront as a function of the activation threshold θ₁₁ and the connection strength γ₁₁, with the permittivity variable set to v = 3.0. The speed of propagation is slow if the threshold of activation θ₁₁ is higher than the value of the fast population activity (u₁) in the interictal state. d Same conventions as in c for a permittivity variable v = 3.2. The speed of propagation remains slow for other values of the permittivity variable