iDoComp: a compression scheme for assembled genomes

Abstract

Motivation: With the release of the latest next-generation sequencing (NGS) machine, the HiSeq X by Illumina, the cost of sequencing a Human has dropped to a mere $4000. Thus we are approaching a milestone in the sequencing history, known as the $1000 genome era, where the sequencing of individuals is affordable, opening the doors to effective personalized medicine. Massive generation of genomic data, including assembled genomes, is expected in the following years. There is crucial need for compression of genomes guaranteed of performing well simultaneously on different species, from simple bacteria to humans, which will ease their transmission, dissemination and analysis. Further, most of the new genomes to be compressed will correspond to individuals of a species from which a reference already exists on the database. Thus, it is natural to propose compression schemes that assume and exploit the availability of such references.

Results: We propose iDoComp, a compressor of assembled genomes presented in FASTA format that compresses an individual genome using a reference genome for both the compression and the decompression. In terms of compression efficiency, iDoComp outperforms previously proposed algorithms in most of the studied cases, with comparable or better running time. For example, we observe compression gains of up to 60% in several cases, including H.sapiens data, when comparing with the best compression performance among the previously proposed algorithms.

Availability: iDoComp is written in C and can be downloaded from: http://www.stanford.edu/~iochoa/iDoComp.html (We also provide a full explanation on how to run the program and an example with all the necessary files to run it.).

Contact: iochoa@stanford.edu

Supplementary information: Supplementary Data are available at Bioinformatics online.

1 Introduction

In 2000, US president Bill Clinton declared the success of the Human Genome Project (Int. Human Genome Sequencing Consortium, 2001), calling it ‘the most important scientific discovery of the 20th century’ (although it was not until 2003 that the human genome assembly was completed). It was the end of a project that took almost 13 years to complete and cost 3 billion dollars ($1 per base pair).

Fortunately, sequencing cost has drastically decreased in recent years. While in 2004 the cost of sequencing a full-human genome was around $20 million, in 2008 it dropped to a million, and in 2014 to a mere $4000 (www.genome.gov/sequencingcosts). Thanks to Illumina’s latest NGS machine, the HiSeq X, we are approaching the $1000 human genome milestone. The rate of this price drop is surpassing Moore’s law, which suggests that efficient compression will be crucial for sustaining this growth. As an example, the sequencing data generated by the 1000 Genomes Project (www.1000genoms.org) in the first 6 months exceeded the sequence data accumulated during 21 years in the NCBI GenBank database (Pennisi, 2011).

The compression algorithms proposed previously in the literature can be classified into two main categories: (i) Compression of raw NGS data (namely FASTQ and SAM/BAM files) and (ii) Compression of assembled data, i.e. the compression of FASTA files containing assembled genomes. See the articles by Zhu et al., 2015 and Deorowicz and Grabowski (2013a) for an extended review. Moreover, within each of these categories the compression can be made either with or without a reference. We focus here on what will likely quickly become a prevalent mode: compression of assembled genomes, with a reference. Specifically, we consider pair-wise compression, i.e. compression of a target genome given a reference available both for the compression and the decompression.

Although there exists a need for compression of raw sequencing data (FASTQ, SAM/BAM), compression of assembled genomes presented in FASTA format is also important. For example, whereas an uncompressed Human genome occupies around 3 GB, its equivalent compressed form is in general smaller than 10 MB, thus easing the transfer and download of genomes, e.g. it can be attached to an email. Moreover, with the improvements in the sequencing technology, increasing amounts of assembled genomes are expected in the near future.

1.1 Compression schemes for assembled genomes

Although there exist general-purpose compression schemes like gzip, bzip2 and 7zip (www.gzip.org, www.bzip.org and www.7zip.org, respectively) that can be directly applied to FASTA files containing assembled genomes, they do not exploit the particularities of these data, yielding relatively low compression gains (Deorowicz and Grabowski, 2013a; Zhu et al., 2015). With this gap in mind in compression ratios, several compression algorithms were proposed in the last two decades. On one hand, dictionary based algorithms as BioCompress2 (Grumbach and Tahi, 1994) and DNACompress (Chen et al., 2002) compress the genome by identifying low complexity substrings as repeats or palindromes and replacing them by the corresponding codeword from the codebook. On the other hand, statistics-based algorithms such as XM (Cao et al., 2007) generate a statistical model of the genome and then use entropy coding that relies on the previously computed probabilities.

Although the aforementioned algorithms perform very well over data of relatively small size, such as mitochondrial DNA, they are impractical for larger sequences (recall that the size of the human genome is on the order of several gigabytes). Further, they focus on compressing a single genome without the use of a reference sequence, and thus do not exploit the similarities across genomes of the same species.

It was in 2009 that interest in reference-based compression started to rise with the publication of DNAzip (Christley et al., 2009) and the proposal from Brandon et al., 2009. In DNAzip, the authors compressed the genome of James Watson (JW) to a mere 4 MB based on the mapping from the JW genome to a human reference and using a public database of the most common single nucleotide polymorphisms (SNPs) existing in humans. Pavlichin et al. (2013) further improved the DNAzip approach by performing a parametric fitting of the distribution of the mapping integers. The main limitation of these two proposals is that they rely on a database of SNPs available only for humans and further assume that the mapping from the target to the reference is given. Thus, while they set a high-performance benchmark for whole human genome compression, they are currently not applicable beyond this specific setting.

Kuruppu et al. (2010a) proposed the Relative Lempel-Ziv Compression of Genomes (RLZ) algorithm for reference-based compression of a set of genomes. The authors improved the algorithm in a subsequent publication, yielding the RLZ-opt algorithm (Kuruppu et al., 2011). The RLZ algorithms are based on parsing the target genome into the reference sequence in order to find longest matches. While in RLZ the parsing is done in a greedy manner (i.e. always selecting the longest match), in the optimized version, RLZ-opt, the authors proposed a non-greedy parsing technique that improved the performance of the previous version. Each of the matches is composed of two values: the position of the reference where the match starts (a.k.a. offset) and the length of the match. Once the set of matches is found, some heuristics are used to reduce the size of the set. For example, short matches may be more efficiently stored as a run of base-pairs (a.k.a. literals) than as a match (i.e. a position and a length). Finally, the remaining set together with the set of literals is entropy encoded.

Deorowicz and Grabowski (2011) proposed the Genome Differential Compressor (GDC) algorithm, which is based on the RLZ-opt. One of the differences between the two is that GDC performs the non-greedy parsing of the target into the reference by hashing rather than using a suffix array. It also performs different heuristics for reducing the size of the set of matches, such as allowing for partial matches and allowing or denying large “jumps” in the reference for subsequent matches. GDC offers several variants, some optimized for compression of large collections of genomes, e.g. the ultra variant. Finally, Deorowicz and Grabowski (2011) showed in their paper that GDC outperforms (in terms of compression ratio) RLZ-opt and, consequently, all the previous algorithms proposed in the literature. It is worth mentioning that the authors of RLZ did create an improved version of RLZ-opt whose performance is similar to that of GDC. However, Deorowicz and Grabowski (2011) showed that it was very slow and that it could not handle a data set with 70 human genomes.

At the same time, two other algorithms, namely GRS and GReEn (Wang and Zhang, 2011) and (Pinho et al., 2012), respectively, were proposed. The main difference between the aforementioned ones and GRS and GReEN is that in the later two the authors only consider the compression of a single genome based on a reference, rather than a set of genomes. Moreover, they assume that the reference is available and need not be compressed. It was shown in (Deorowiczand Grabowski, 2011; Pinho et al., 2012) that GRS only considers pairs of targets and references that are very similar. Pinho et al., 2012 proposed an algorithm based on arithmetic coding. They use the reference to generate the statistics and then they perform the compression of the target using arithmetic coding, which uses the previously computed statistics. They showed clearly that GReEn was superior to both GRS and the non-optimized RLZ. However, Zhu et al., 2015 showed in their review paper that there were some cases where GRS clearly outperformed GReEn in both compression ratio and speed. Interestingly, this phenomenon was observed only in cases of bacteria and yeast, which have genomes of relatively small size.

In 2012, another compression algorithm was presented in (Chern et al., 2012), where they showed some improved compression results with respect to GReEn. However, the algorithm they proposed has relatively high running time when applied to big datasets and it does not work in several cases (see Supplementary Data, Section VI for the results.). Also in 2012, Wandelt and Ulf, 2012 proposed a compression algorithm for single genomes that trades off compression time and space requirements while achieving comparable compression rates to that of GDC. The algorithm divides the reference sequence in blocks of fixed size, and constructs a suffix tree for each of the blocks, which are later used to parse the target into the reference.

Although it is straightforward to adapt GReEn to the database scenario in order to compare it with the other state-of-the-art algorithm GDC, in the review paper by Zhu et al., 2015 they did not perform any comparison between them. Moreover, the algorithm introduced in Wandelt and Ulf, 2012 was not mentioned. On the other hand, in the review paper by Deorowicz and Grabowski, 2013a the authors did compare all the algorithms stating that GDC and (Wandelt and Ulf, 2012) achieved the highest compression ratios. However, no empirical evidence in support of that statement was shown in the article. Finally, in (Deorowicz et al., 2013b) they showed that GDC achieved better compression ratios than (Wandelt and Ulf, 2012) in the considered data sets.

After having examined all the available comparisons in the literature, we consider GReEN and GDC to be the state-of-the-art algorithms in reference-based genomic data compression. Thus, we use these algorithms as benchmark. (We do not use the algorithm proposed in (Wandelt et al., 2012) because we were unable to run the algorithm.) However, we also add GRS to the comparison base in the cases where (Zhu et al., 2015) showed that GRS outperformed GReEn.

Although in this work we do not focus on compression of collection of genomes, for completeness we introduce the main algorithms designed for this task. As mentioned above, the version GDC-Ultra introduced in (Deorowicz and Grabowski, 2011) specializes in compression of a collection of genomes. In 2013, a new algorithm designed for the same purpose, FRESCO, was presented in (Wandelt and Ulf, 2013). The main innovations of FRESCO include a method for reference selection and reference rewriting, and an implementation of a second-order compression. FRESCO offers lower running times than GDC-Ultra, with comparable compression ratios. Finally, in Deorowicz et al. (2013b) they showed that in this scenario a boost in compression ratio is possible if one considers the genomes are given as variations with respect to a reference, in VCF format (Danecek et al., 2011), and the similarity of the variations across genomes is exploited.

In the next section we present the proposed algorithm iDoComp. It is based on a combination of ideas proposed in Christley et al. (2009), Brandon et al. (2009) and Chern et al. (2012).

2 Methods and algorithms

In this section, we start by describing the proposed algorithm iDoComp, whose goal is to compress an individual genome assuming a reference is available both for the compression and the decompression. We then present the data used to compare the performance of the different algorithms, and the machine specifications where the simulations were conducted.

2.1 iDoComp

The input to the algorithm is a target string $T\in {\Sigma }^t$ of length t over the alphabet Σ, and a reference string $S\in {\Sigma }^s$ of length s over the same alphabet. Note that, in contrast to (Kuruppu et al., 2011), the algorithm does not impose the condition that the specific pair of target and reference contain the same characters, e.g. the target T may contain the character N even if it is not present in the reference S. As outlined above, the goal of iDoComp is to compress the target sequence T using only the reference sequence S, i.e. no other aid is provided to the algorithm.

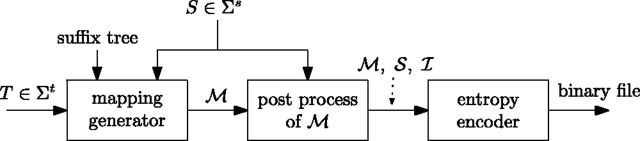
iDoComp is composed of mainly three steps (see Fig. 1): (i) the mapping generation, whose aim is to express the target genome T in terms of the reference genome S, (ii) the post-processing of the mapping, geared toward decreasing the prospective size of the mapping, and (iii) the entropy encoder, that further compresses the mapping and generates the compressed file. Next, we describe these steps in more detail.

Fig. 1.

Diagram of the main steps of the proposed algorithm iDoComp

2.1.1 Mapping generation

The goal of this step is to create the parsing of the sequence T relative to S. A parsing of T relative to S is defined as a sequence $({\omega }_1,{\omega }_2,\dots ,{\omega }_N)$ of substrings of S that when concatenated together in order yield the target sequence T. For reasons that will become clear later, we slightly modify the above definition and re-define the parsing as $({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_N)$, where ${\tilde{\omega }}_i=({\omega }_i,C_i)$, ω_i being a sub-string of S and $C_i\in \Sigma$ a mismatched character that appears after ω_i in T but not in S. Note that the concatenation of the $\tilde{\omega }$, i.e. both the sub-strings and mismatched characters, should still yield the target sequence T.

A very useful way of expressing the sub-string ${\tilde{\omega }}_i$ is as the triplet $m_i=(p_i,l_i,C_i)$, with $p_i,l_i\in (1,\dots ,s)$, where p_i is the position in the reference where ω_i starts and l_i is the length of ω_i. If there is a letter X in the target that does not appear in the reference, then the match $(p_{i-1}+l_{i-1},0,X)$ will be generated, where $p_{i-1}$ and $l_{i-1}$ are the position and length of the previous match, respectively (We assume $p_0=l_0=0$.). In addition, note that if ω_i appears in more than one place in the reference, any of the starting positions is a valid choice.

With this notation, the parsing of T relative to S can be defined as the sequence of matches $\mathcal{M}={\{m_i=(p_i,l_i,C_i)\}}_{i=1}^N$.

In this work, we propose the use of suffix arrays to parse the target into the reference due to its attractive memory requirements, especially when compared to other index structures such as suffix trees (Gusfield, 1997). This makes the compression and decompression of a human genome doable on a computer with a mere 2 GB of RAM. Also, the use of suffix arrays is only needed for compression, i.e. no suffix arrays are used for the decompression. Finally, we assume throughout the paper that the suffix array of the reference is already pre-computed and stored in the hard drive.

Once the suffix array of the reference is loaded into memory, we perform a greedy parsing of the target as previously described to obtain the sequence of matches $\mathcal{M}={\left\{m_i\right\}}_{i=1}^N$ (A detailed description of this step is provided in the Supplementary Data, Section II). Deorowicz and Grabowski (2011) and Kuruppu et al. (2011) showed that a greedy parsing leads to suboptimal results. However, we are not performing the greedy parsing as described in (Kuruppu et al., 2010b), since every time a mismatch is found we record the mismatched letter and advance one position in the target. Since most of the variations between genomes of different individuals within the same species are SNPs (substitutions), recording the mismatch character leads to a more efficient ‘greedy’ mapping.

Moreover, note that at this stage the sequence of matches $\mathcal{M}$ suffices to reconstruct the target sequence T given the reference sequence S. However, in the next step we perform some post-processing over $\mathcal{M}$ in order to reduce its prospective size, which will translate to better compression ratios. This is similar to the heuristic used by (Deorowicz and Grabowski, 2011) and (Kuruppu et al., 2011) for their non-greedy mapping.

2.1.2 Postprocessing of the sequence of matches $\mathcal{M}$

After the sequence of matches $\mathcal{M}$ is computed, a post-processing is performed on them. The goal is to reduce the total number of elements that will be later compressed by the entropy encoder. Recall that each of the matches m_i contained in $\mathcal{M}$ is composed of two integers in the range $(1,\dots ,s)$ and a character on the alphabet Σ. Since $|\Sigma |\ll s$, the number of unique integers that appear in $\mathcal{M}$ will be in general larger than $|\Sigma |$. Thus, the compression of the integers will require in general more bits than those needed to compress the characters. Therefore, the aim of this step is mainly to reduce the number of different integers needed to represent T as a parse of S, which will translate to improved compression ratios.

Specifically, in the post-processing step we look for consecutive matches $m_{i-1}$ and m_i that can be merged together and converted into an approximate match. By doing this we reduce the cardinality of $\mathcal{M}$ at a cost of storing the divergences of the approximate matchings with regards to the exact matchings. We classify these divergences as either SNPs (substitutions) or insertions, forming the new sets $\mathcal{S}$ and $\mathcal{I}$, respectively.

For the case of the SNPs, if we find two consecutive matches $m_{i-1}$ and m_i that can be merged at the cost of recording a SNP that occurs between them, we add to the set $\mathcal{S}$ an element of the form $s_i=(p_i,C_i)$, where p_i is the position of the target where the SNP occurs, with $T[p_i]=C_i$. Then we merge matches $m_{i-1}$ and m_i together into a new match $m\leftarrow (p_{i-1},l_{i-1}+l_i+1,C_i)$. Hence, with this simple process we have reduced the number of integers from 4 to 3.

We constrain the insertions to be of length one; that is, we do not explicitly store short runs of literals (together with its position and length). This is in contrast to the argument of Deorowicz and Grabowski (2011) and Kuruppu et al. (2011) stating that storing short runs of literals is more efficient than storing their respective matching. However, as we show next, we store them as a concatenation of SNPs. Although this might seem inefficient, the motivation behind it is that storing short runs of literals will in general add new unique integers, which incurs a high cost, since the entropy encoder (based on arithmetic coding) will assign to them a larger amount of bits. We found that encoding them as SNPs and then storing the difference between consecutive positions of SNPs is more efficient. This process is explained next in more detail.

As pointed out by Kuruppu et al. (2011), the majority of the matches m_i belong to the Longest Increasing Sub-Sequence (LISS) of the p_i. In other words, most of the consecutive p_i’s satisfy $p_i\le p_{i+1}\le \dots \le p_j$, for i < j, and thus they belong to the LISS. From the m_i’s whose p_i value does not belong to the LISS, we examine those whose length l_i is less than a given parameter L and whose gap to their contiguous instruction is more than Δ. Among them, those whose number of SNPs is less than a given parameter ρ, or are short enough ($<\Lambda$), are classified as several SNPs.

That is, if the match m_i fulfills any of the above conditions, we merge the instructions $m_{i-1}$ and m_i as described above. Note that the match m_i was pointing to the length l_i sub-string starting at position p_i of the reference, whereas now (after merging it to $m_{i-1}$) it points to the one that starts at position $p_{i-1}+l_{i-1}+1$. Therefore, we need to add to the set $\mathcal{S}$ as many SNPs as differences between these two substrings.

Note that this operation gets rid of the small-length matches whose p_i’s are far apart from their “natural” position in the LISS. These particular matches will harm our compression scheme as they generate new large integers in most of the cases. On the other hand, if the matches were either long, or with several SNP’s, and/or extremely close to their contiguous matchings, then storing them as SNP’s would not be beneficial. Therefore, the values of L, Δ, ρ and Λ are chosen such that the expected size of the new generated subset of SNPs is less than that of the match m_i under consideration. This procedure is similar to the heuristic used by Deorowicz and Grabowski (2011) to allow or deny ‘jumps’ in the reference while computing the parsing.

The flowchart of this part of the post-processing is depicted in Figure 2. For a more detailed flowchart, we refer the reader to the Supplementary Data, Section III.

Fig. 2.

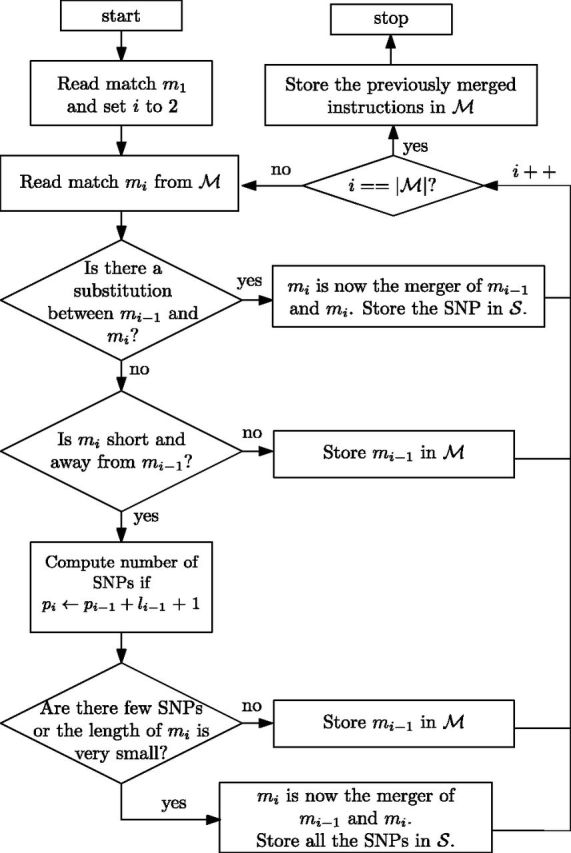
Flowchart of the post-processing of the sequence of matches $\mathcal{M}$ to generate the set $\mathcal{S}$

We perform an analogous procedure to find insertions in the sequence of matches $\mathcal{M}$. Since we only consider length-1 insertions, each insertion in the set $\mathcal{I}$ is of the form (p, C), where p indicates the position in the target where the insertion occurs, and C the character to be inserted. As mentioned earlier, the short runs of literals have been taken care of in the last step of the SNP set generation.

After the postprocessing described above is concluded, the sequence of matches $\mathcal{M}$ and the two sets $\mathcal{S}$ and $\mathcal{I}$ are fed to the entropy encoder.

2.1.3 Entropy encoder

The goal of the entropy encoder is to compress the instructions contained in the sequence of matches $\mathcal{M}$ and the sets $\mathcal{S},\mathcal{I}$ generated in the two previous steps. Recall that the elements in $\mathcal{M},\mathcal{S}$, and $\mathcal{I}$ are given by integers and/or characters, which will be compressed in a different manner. Specifically, we first create two vectors $\mathbf{\pi }$ and $\mathit{\gamma }$ containing all the integers and characters, respectively, from $\mathcal{M},\mathcal{S}$, and $\mathcal{I}$. In order to be able to determine to which instruction each integer and character belongs, at the beginning of $\mathit{\pi }$ we add the cardinalities of $\mathcal{M},\mathcal{S}$, and $\mathcal{I}$, as well as the number of chromosomes.

To store the integers, first note that all the positions p_i in $\mathcal{S}$ and $\mathcal{I}$ are ordered in ascending order, thus we can freely store the p_i’s as $p_i\leftarrow p_i-p_{i-1}$, for $i\ge 2$; that is, as the difference between successive ones. We perform a similar computation with the p_i’s of $\mathcal{M}$. Specifically, we store each p_i as $p_i\leftarrow |p_i-(p_{i-1}+l_{i-1})|$, for $i\ge 2$. However, since some of the matches may not belong to the LISS, there will be cases where $p_{i-1}+l_{i-1}>p_i$. Hence, a sign vector s is needed in this case to save the sign of the newly computed positions in $\mathcal{M}$. Finally, the lengths $l_i\in \mathcal{M}$ are also stored in $\mathit{\pi }$.

Once the vector $\mathit{\pi }$ is constructed, it is encoded by a byte-based adaptive arithmetic encoder, yielding the binary stream $A_{\pi }(\mathit{\pi })$. Specifically, we represent each integer with 4 B , and encode each of the bytes independently, i.e. with a different model. (We chose 4 B as it is the least number of bytes needed to represent all possible integers.) This avoids the need of having to store the alphabet, which can be a large overhead in some cases. Moreover, the statistics of each of the bytes are updated sequentially (adaptively), and thus they do not need to be previously computed.

The vector $\mathit{\gamma }$ is constructed by storing all the characters belonging to $\mathcal{M},\mathcal{S}$, and $\mathcal{I}$. First, note that since the reference is available at both the encoder and the decoder, they both can access any position of the reference. Thus, for each of the characters $C_i\in \mathit{\gamma }$ we can access its corresponding mismatched character in the reference, that we denote as R_i. Thus, we generate a tuple of the form (R, C) for all the mismatched characters of the parsing. We then employ a different model for the adaptive Arithmetic encoder for each of the different R’s, and encode each $C_i\in \mathit{\gamma }$ using the model associated to its corresponding R_i. Note that by doing this, one or two bits per letter can be saved in comparison with the traditional one-code-for-all approach.

Finally, the binary output stream is the concatenation of $A_{\pi }(\mathit{\pi })$, s and $A_{\gamma }(\mathit{\gamma })$ (the arithmetic-compressed vector $\mathit{\gamma }$).

2.2 Data

To assess the performance of the proposed algorithm iDoComp, we consider pair-wise compression applied to different datasets. Specifically, we consider the scenario where a reference genome is used to compress another individual of the same species (the target genome). (The target and the reference do not necessarily need to belong to the same species, although better compression ratios are achieved if the target and the reference are highly similar.) This would be the case when there is already a database of sequences from a particular species, and a new genome of the same species is assembled and thus needs to be stored (and therefore compressed).

The data used for the pair-wise compression are summarized in Table 1. This scenario was already considered (Brandon et al., 2009; Christley et al., 2009; Deorowicz and Grabowski, 2011; Pinho et al., 2012; Wang and Zhang, 2011; Zhu et al., 2015) for assessing the performance of their algorithms, and thus the data presented in Table 1 include the ensemble of all the datasets used in the previously mentioned articles.

Table 1.

Genomic sequence datasets used for the pair-wise compression evaluation

Species	Chr.		Assembly	Retrieved from
L.pneumohilia	1	T:	NC_017526.1	ncbi.nlm.nih.gov
		R:	NC_017525.1
E.coli	1	T:	NC_017652.1	ncbi.nlm.nih.gov
		R:	NC_017651.1
S.cerevisiae	17	T:	sacCer3	ucsc.edu
		R:	sacCer2
C.elegans	7	T:	ce10	genome.ucsc.edu
		R:	ce6
A.thaliana	7	T:	TAIR10	arabidopsis.org
		R:	TAIR9
Oryza sativa	12	T:	TIGR6.0	rice.plantbiology.msu.edu
		R:	TIGR5.0
D.melanogaster	6	T:	dmelr41	fruitfly.org
		R:	dmelr31
H.sapiens 1	25	T:	hg19	ncbi.nlm.nih.gov
		R:	hg18
H.sapiens 2	25	T:	KOREF_20090224	koreangenome.org
		R:	KOREF_20090131
H.sapiens 3	25	T:	YH	yh.genomics.org.cn
		R:	hg18	ncbi.nlm.nih.gov
H.sapiens 4	25	T:	hg18	ncbi.nlm.nih.gov
		R:	YH	yh.genomics.org.cn
H.sapiens 5	25	T:	YH	yh.genomics.org.cn
		R:	hg19	ncbi.nlm.nih.gov
H.sapiens 6	25	T:	hg18	ncbi.nlm.nih.gov
		R:	hg19

Note: Each row specifies the species, the number of chromosomes they contain and the target and the reference assemblies with the corresponding locations from which they were retrieved. T. and R. stand for the Target and the Reference, respectively.

As evident in Table 1, we include in our simulations datasets from a variety of species. These datasets are also of very different characteristics in terms for example of the alphabet size, the number of chromosomes they include, and the total length of the target genome that needs to be compressed.

2.3 Machine specifications

The machine used to perform the experiments and estimate the running time of the different algorithms has the following specifications: 39 GB RAM, Intel Core i7-930 CPU at 2.80 GHz × 8 and Ubuntu 12.04 LTS.

3 Results

Next we show the performance of the proposed algorithm iDoComp in terms of both compression and running time, and compare the results with the previously proposed compression algorithms.

As mentioned, we consider pair-wise compression for assessing the performance of the proposed algorithm. Specifically, we consider the compression of a single genome (target genome) given a reference genome available both at the compression and the decompression. We use the target and reference pairs introduced in Table 1 to assess the performance of the algorithm. Although in all the simulations the target and the reference belong to the same species, note that this is not a requirement of iDoComp, which also works for the case where the genomes are from different species.

To evaluate the performance of the different algorithms, we look at the compression ratio, as well as at the running time of both the compression and the decompression. We compare the performance of iDoComp with those of GDC, GReEn, and GRS.

When performing the simulations, we run both GReEn and GRS with the default parameters. The results presented for GDC correspond to the best compression among the advanced and the normal variant configurations, as specified in the Supplementary Data presented in Deorowicz and Grabowski (2011). Note that the parameter configuration for the H.sapiens differs from that of the other species. We modify it accordingly for the different datasets. Regarding iDoComp, all the simulations are performed with the same parameters (default parameters), which are hard-coded in the code (Please refer to the Supplementary Data, Section IV for more information regarding the values of the default parameters used for the simulations in iDoComp, as well as for the versions and options used for the other algorithms.).

For ease of exhibition, for each simulation we only show the results of iDoComp, GDC and the best among GReEn and GRS. The results are summarized in Table 2. For each species, the target and the reference are as specified in Table 1. To be fair across the different algorithms, especially when comparing the results obtained in the small datasets, we do not include the cost of storing the headers in the computation of the final size for any of the algorithms. The last two columns show the gain obtained by our algorithm iDoComp with respect to the performance of GReEn/GRS and GDC. For example, a reduction from 100 kB to 80 kB represents a 20% gain (improvement). Note that with this metric a 0% gain means the file size remains the same, a 100% improvement is not possible, as this will mean the new file is of size 0, and a negative gain means that the new file is of bigger size.

Table 2.

Compression results for the pairwise compression

Species	Raw Size	GReEn/GRSa			GDC			iDoComp			Gain
	(MB)	Size (kB)	C. time	D. time	Size (kB)	C. time	D. time	Size (kB)	C. time	D. time	GR	GDC
L.pneumohilia	2.7	0.122a	1a	1a	0.229b	0.3	0.03	0.084	0.1	0.1	31%	63%
E.coli	5.1	0.119	1	0.6	0.242b	0.6	0.06	0.086	0.2	0.2	30%	64%
S.cerevisiae	12.4	5.65a	5a	5a	6.47b	1	1	2.53	0.4	0.4	55%	61%
C.elegans	102.3	170	45	47	48.7	1	1	13.3	3	4	92%	73%
A.thaliana	121.2	6.6	54	56	6.32	21	2	2.09	4	5	68%	67%
O.sativa	378.5	125.5	140	146	128.6b	80	6	105.4	11	15	16%	18%
D.melanogaster	120.7	390.6	51	2	433.7	23	1	364.4	4	4	7%	16%
H.sapiens 1	3100	11 200	1687	1701	2770	2636	67	1025	95	130	91%	63%
H.sapiens 2	3100	18 000	652	721	11 973	511	78	7247	120	126	60%	39%
H.sapiens 3	3100	10 300	434	495	6840	141	65	6290	118	125	39%	8%
H.sapiens 4	3100	6500	352	372	6426	191	70	5767	115	130	11%	10%
H.sapiens 5	3100	35 500	1761	1846	11 873b	249	62	11 560	122	130	67%	3%
H.sapiens 6	3100	10 560	1686	1775	6939	2348	70	5241	100	120	50%	24%

Note: C. time and D. time stand for compression and decompression time (s), respectively. The results in bold correspond to the best compression performance among the different algorithms. We use the International System of Units for the prefixes, that is, 1 MB and 1 kB stands for 10⁶ and 10³ bytes, respectively.

^aDenotes the cases where GRS outperformed GReEn. In these cases, i.e. L.pneumohilia and S.cerevisiae, the compression achieved by GReEn is 495 kB and 304.2 kB, respectively.

^bDenotes the cases where GDC-advanced outperformed GDC normal.

As seen in Table 2, the proposed algorithm outperforms in compression ratio the previously proposed algorithms in all cases. Moreover, we observe that whereas GReEn/GRS seem to achieve better compression in those datasets that are small and GDC in the H.sapiens datasets, iDoComp achieves good compression ratios in all the datasets, regardless of their size, the alphabet and/or the species under consideration.

In cases of bacteria (small size DNA), the proposed algorithm obtains compression gains that vary from 30% against GReEn/GRS to up to 64% when compared with GDC. For the S.cerevisae dataset, also of small size, iDoComp does 55% (61%) better in compression ratio than GRS (GDC). For the case of medium size DNA (C.elegans, A.thaliana, O.sativa and D.melanogaster) we observe similar results. iDoComp again outperforms the other algorithms in terms of compression, with gains up to 92%.

Finally, for the H.sapiens datasets, we observe that iDoComp consistently performs better than GReEn, with gains above 50% in four out of the six datasets considered, and up to 91%. With respect to GDC, we also observe that iDoComp produces better compression results, with gains that vary from 3% to 63%.

Based on these results, we can conclude that GDC and the proposed algorithm iDoComp are the ones that produce better compression results on the H.sapiens genomes. In order to get more insight into the compression capabilities of both algorithms when dealing with Human genomes, in the Supplementary Data, Section VII we provide more simulation results. Specifically, we simulate twenty pair-wise compressions, and show that on average iDoComp employs 7.7 MB per genome, whereas GDC employs 8.4 MB. Moreover, the gain of iDoComp with respect to GDC for the considered cases is on average 9.92%.

Regarding the running time, we observe that the compression and the decompression time employed by iDoComp is linearly dependent on the size of the target to be compressed. This is not the case of GReEn, for example, whose running times are highly variable. In GDC we also observe some variability in the time needed for compression. However, the decompression time is more consistent among the different datasets (in terms of the size), and it is in general the smallest among all the algorithms we considered. iDoComp and GReEn take approximately the same time to compress and decompress. Overall, iDoComp’s running time is seen to be highly competitive with that of the existing methods. However, note that the time needed to generate the suffix array is not counted in the compression time of iDoComp, whereas the compression time of the other algorithms may include construction of index structures, like in the case of GDC (see the Supplementary Data, Section V for details on the construction of the suffix arrays.).

Finally, we briefly discuss the memory consumption of the different algorithms. We focus on the compression and decompression of the H.sapiens datasets, as they represent the larger files and thus the memory consumption in those cases is the most significant. iDoComp employs around 1.2 GB for compression, and around 2 GB for decompression. GReEn consumes around 1.7 GB both for compression and decompression. Finally, the algorithm GDC employs 0.9 GB for compression and 0.7 GB for decompression.

4 Discussion

Inspection of the empirical results of the previous section shows the superior performance of the proposed scheme across a wide range of datasets, from simple bacteria to the more complex humans, without the need of adjusting any parameters. This is a clear advantage over algorithms like GDC, where the configuration must be modified depending on the species being compressed.

Although iDoComp has some internal parameters, namely, L, Δ, Λ and ρ, the default values that are hard-coded in the code perform very well for all the datasets, as we have shown in the previous section. (See the Post-Processing step in section 2 for more details.) However, the user could modify these parameters data-dependently and achieve better compression ratios. Future work will explore the extent of the performance gain (which we believe will be substantial) due to optimizing for these parameters.

We believe that the improved compression ratios achieved by iDoComp are due largely to the post-processing step of the algorithm, which modifies the set of instructions in a way that is beneficial to the entropy encoder. In other words, we modify the elements contained in the sets so as to facilitate their compression by the arithmetic encoder.

Moreover, the proposed scheme is universal in the sense that it works regardless of the alphabet used by the FASTA files containing the genomic data. This is also the case with GDC and GReEn, but not with previous algorithms like GRS or RLZ-opt which only work with A, C, G, T, and N as the alphabet.

It is also worth mentioning that the reconstructed files of both iDoComp and GDC are exactly the original files, whereas the reconstructed files under GReEn do not include the header and the sequence is expressed in a single line (instead of several lines).

Another advantage of the proposed algorithm is that the scheme employed for compression is very intuitive, in the sense that the compression consists mainly of generating instructions composed of the sequence of matches $\mathcal{M}$ and the two sets $\mathcal{S}$ and $\mathcal{I}$ that suffice to reconstruct the target genome given the reference genome. This information by itself can be beneficial for researchers and gives insight into how two genomes are related to each other. Moreover, the list of SNPs generated by our algorithm could be compared with available datasets of known SNPs. For example, the NCBI dbSNP database contains known SNPs of the H.sapiens species.

Finally, regarding iDoComp, note that we have not included in Table 2 the time needed to generate the suffix array of the reference, only that needed to load it into memory, which is already included in the total compression time. (We refer the reader to the Supplementary Data, Section V for information on the time needed to generate the suffix arrays.) The reason is that we devise these algorithms based on pair-wise compression as the perfect tool for compressing several individuals of the same species. In this scenario, one can always use the same reference for compression, and thus the suffix array can be reused as many times as the number of new genomes that need to be compressed.

Regarding compression of sets, any pair-wise compression algorithm can be trivially used to compress a set of genomes. One has merely to choose a reference and then compress each genome in the set against the chosen reference. However, as was shown in Deorowicz and Grabowski (2011) with their GDC-ultra version of the algorithm, and as can be expected, an intelligent selection of the references can lead to significant boosts in the compression ratios. Therefore, in order to obtain high compression ratios in sets it is of ultimate importance to provide the pair-wise compression algorithms with a good reference-finding method. This could be thought of as an add-on that could be applied to any pair-wise compression algorithm. For example, one could first analyze the genomes contained in the set to detect similarity among genomes, and then use this information to boost the final compression. (A similar approach is used in Wandelt et al. (2013) The latter is a different problem that needs to (and will) be addressed separately. However, for completeness, we have included some results on compression of sets and on the influence of the choice of the reference in the Supplementary Data, Sections VIII and IX.

5 Conclusion

In this article, we introduce iDoComp, an algorithm for compression of assembled genomes. Specifically, the algorithm considers pair-wise compression, i.e. compression of a target genome given that a reference genome is available both for the compression and the decompression. This algorithm is universal in the sense of being applicable for any dataset, from simple bacteria to more complex organisms such as humans, and accepts genomic sequences of an extended alphabet. We show that the proposed algorithm achieves better compression than the previously proposed algorithms in the literature, in most cases. These gains are up to 92% in medium size DNA and up to 91% in humans when compared with GReEn and GRS. When compared with GDC, the gains are up to 73% and 63% in medium size DNA and humans, respectively.

Funding

This work is partially funded by a Stanford Graduate Fellowships Program in Science and Engineering, a fellowship from the Basque Government, a grant from the Center for Science of Information (CSoI) and 1157849-1-QAZCC NSF grant.

Conflict of interest: none declared.