Evolutionary dynamics of the leaf phenological cycle in an oak metapopulation along an elevation gradient

Abstract

It has been predicted that environmental changes will radically alter the selective pressures on phenological traits. Long-lived species, such as trees, will be particularly affected, as they may need to undergo major adaptive change over only one or a few generations. The traits describing the annual life cycle of trees are generally highly evolvable, but nothing is known about the strength of their genetic correlations. Tight correlations can impose strong evolutionary constraints, potentially hampering the adaptation of multivariate phenological phenotypes. In this study, we investigated the evolutionary, genetic and environmental components of the timing of leaf unfolding and senescence within an oak metapopulation along an elevation gradient. Population divergence, estimated from in situ and common garden data, was compared to expectations under neutral selection, based on microsatellite markers. This approach made it possible (1) to evaluate the influence of genetic correlation on multivariate local adaptation to elevation and (2) to identify traits probably exposed to past selective pressures due to the colder climate at high elevation. The genetic correlation was positive but very weak, indicating that genetic constraints did not shape the local adaptation pattern for leaf phenology. Both spring and fall (leaf unfolding and senescence, respectively) phenology timings were involved in local adaptation, but leaf unfolding was probably the trait most exposed to climate change-induced selection. Our data indicated that genetic variation makes a much smaller contribution to adaptation than the considerable plastic variation displayed by a tree during its lifetime. The evolutionary potential of leaf phenology is, therefore, probably not the most critical aspect for short-term population survival in a changing climate.

Introduction

The capacity of populations to cope with environmental changes depends on their ability to track a fitness optimum moving over the phenotypic space. This process involves adaptive plasticity (environmentally induced phenotypic change) and non-neutral genetic changes (microevolution) (Nussey et al., 2007; Lande, 2009). The contribution of microevolution to short-term responses to new climatic conditions remains a matter of debate (Gienapp et al., 2008; Merilä, 2012; Franks et al., 2014; Teplitsky & Millien, 2014). By contrast, climate has long been recognized to be a major, ubiquitous driver of evolutionary dynamics over longer time scales (Hunt & Roy, 2006; Erwin, 2009).

Plastic responses may be insufficient for immediate fitness optimum tracking. In this situation, the existence of abundant additive genetic variation for traits important for fitness is particularly crucial for the survival of tree populations exposed to climatic variation (Kremer et al., 2014). Trees are sessile, perennial organisms, and, as such, they have slow migration rates, hampering the spatial tracking of their climatic niche (Aitken et al., 2008; Lindner et al., 2010). Furthermore, trees have long generation times, and they may therefore have to adapt to abrupt changes in environmental conditions over only one or a few generations. This is the case for individuals colonizing extreme environments, from established populations that may be exposed to sudden environmental changes. The capacity for evolutionary change therefore depends principally on standing genetic variation in tree populations. Detailed quantitative genetics investigations are therefore required to understand the contribution of selection-based adaptive responses to environmental change in tree populations.

Such investigations must include: (1) measurement of the loss of fitness due to a new environment (i.e., the strength of directional and stabilizing selection on traits of adaptive significance) (Lande & Arnold, 1983) and (2) evaluation of the distribution of genetic variation for traits subject to climatic selection. It is difficult to assess the loss of fitness in species mating over long distances, such as trees. This task therefore requires the use of molecular marker information to assign offspring to parents within a spatially explicit context (e.g., Klein et al., 2011). Estimation of the distribution of genetic variation for fitness-related traits is more straightforward. Such estimations are commonly made in open-pollinated progeny tests in common garden experiments, in which genetic variance can be estimated together with genetic differentiation between populations (reviewed in Alberto et al., 2013a). This makes it possible to compare within-population genetic variability to the genetic divergence of populations along a climatic gradient. Inferences can then be made about the ways in which climate-related selective processes have interacted with the genetic architecture of traits to shape the observed evolutionary trajectories.

Such inferences are based on the theory of multivariate genetic constraints first formalized by Lande (1979) as $\Delta \overline{z}=\mathbf{\text{G}}\beta .$ In other words, the magnitude of the mean phenotypic change $\Delta \overline{z}$ of a set of traits z_i exposed to a multivariate selection gradient β depends on G, the matrix of the additive genetic variance and covariance of the traits. Genetic covariances between traits typically result from pleiotropy or linkage disequilibrium. The ways in which these processes influence evolution and adaptation is thus accounted for by the G matrix, and there is growing evidence to suggest that G can predict the trajectory of phenotypic evolution (Hansen & Houle, 2008; Bolstad et al., 2014; Teplitsky et al., 2014b).

When considering the response to selection of a focal trait z_i, ignoring its genetic covariation with other traits may lead to misleading conclusions. If z_i is correlated with other traits subject to stabilizing selection (or to directional selection acting in the opposite direction to that acting on z_i), part of the evolutionary potential of z_i is captured by selective constraints in other dimensions of the phenotypic space (i.e., the concept of conditional genetic variance introduced by Hansen, 2003). In this case, the adaptive potential of populations facing environmental changes can be overestimated (Etterson & Shaw, 2001; Duputié et al., 2012). Conversely, if the directional selection vector aligns with the main axes of genetic variation in the multivariate phenotypic space, the response to selection may be accelerated (e.g., Schluter, 1996; Hansen & Voje, 2011), highlighting the limitations of univariate approaches focusing on a single key phenotypic trait.

Phenological traits — the dates or durations of key events in the lifecycle of the organism — are typically expected to be exposed to selection induced by environmental change (Rehfeldt et al., 1999; Forrest & Miller-Rushing, 2010; Gienapp et al., 2014). The phenological cycle of the leaves of deciduous temperate tree species can be described on the basis of two timing traits: the date of leaf unfolding (LU) and the date of leaf senescence (LS). Canopy duration (CD) is also a highly biologically meaningful trait as it determines annual growth (Churkina et al., 2005). However, this third trait cannot be considered to be independent, as it is determined by the other two timing traits: CD = LS – LU. Genetic differentiation between populations has been documented for various phenological measurements in several tree species (review in: Alberto et al., 2013a).

Spring phenology (here LU) is known to be highly sensitive to new climatic conditions and has therefore been investigated in detail (Aitken et al., 2008; Alberto et al., 2013a). By contrast, fall phenology has been largely neglected (Gallinat et al., 2015), but several recent studies have highlighted its importance for deciduous tree populations in the context of global warming (Gill et al., 2015; Xie et al., 2015). Investigations of the evolutionary relevance of the various biological aspects of adaptation to climate will require the positioning of the phenological cycle within a multivariate quantitative genetic framework for exploring the evolutionary interplay between spring and fall phenology. Leaf phenological traits in the spring and fall have been shown to be positively correlated between years, at the scale of the ecosystem (Keenan & Richardson, 2015). However, it remains unclear whether this correlation has a genetic basis.

The different biological implications of the three traits described above may explain why they are usually analyzed separately (e.g. Savolainen et al., 2004; Alberto et al., 2011). For example, in oaks, leaf unfolding takes place at the same time as flowering and pollen emission. Thus, assortative mating through long-distance pollen flows would be expected to interact with local adaptation in the evolution of this trait (Soularue & Kremer, 2012; 2014). No such interaction would be expected for the date of leaf senescence. The timing of leaf senescence in the fall is influenced by photoperiod (Richardson et al., 2006; Delpierre et al., 2009; Vitasse et al., 2011), whereas the principal environmental factor controlling leaf unfolding date is temperature (Menzel & Fabian, 1999; Chmielewski & Rötzer, 2001; Vitasse et al., 2009c). Earlier flushing and later senescence dates maximize canopy duration, resulting in a longer period of photosynthetic activity and faster growth, with possible increases in seed production (Caignard et al., 2017) and tree fitness. However, these two “timing” traits are both subject to a trade-off between the maximization of canopy duration on the one hand (favoring earlier flushing and later senescence) and the avoidance of late-spring and early-fall frost damage to the canopy on the other (favoring later flushing and earlier senescence). Canopy frost damage is associated with high fitness costs (for a review: Vitasse et al., 2014), including physical damage to soft tissues in the spring and leaf abscission before the total resorption of nitrogen content by hard tissues in the fall (Norby et al., 2003). Days are longer and solar radiation is stronger in spring than in the fall, so the gain of one day of photosynthesis in the spring is more beneficial than the gain of an extra day in the fall (Vitasse et al., 2009c). Conversely, frost damage on young tissues in the spring is likely to compromise the entire photosynthetic period, whereas frost damage to older leaf tissues in the fall would have a much lesser impact. Thus, the fitness trade-off for timing traits would be expected to be more critical in the spring, for leaf unfolding date.

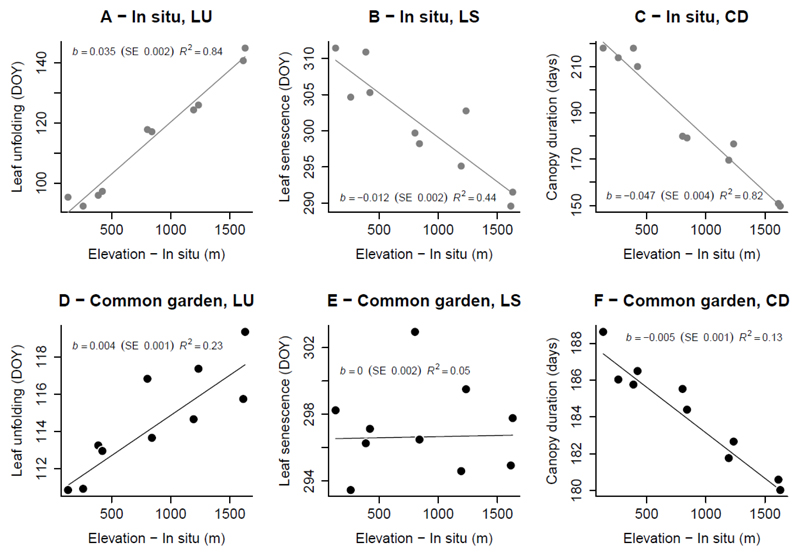
We studied sessile oak (Quercus petraea (Matt.) Liebl.) populations spread along a replicated elevation gradient in two valleys in the Pyrenees (France). The distribution of these populations encompasses the entire elevation range for this species in the Pyrenees (100 – 1600 m), and previous studies have documented substantial phenotypic and genetic covariation of phenological traits with elevation (Vitasse et al., 2009a; Alberto et al., 2011). Indeed, in situ, high-elevation populations (Fig. 1, A, B, C) flush, on average, about 52 days later, and senesce about 18 days earlier than low-elevation populations, and therefore have a shorter canopy duration, of about 70 days (all coefficients are displayed in the panels of Fig. 1). Common garden (Fig. 1, D, E, F) populations from high elevations flush six days later and have a canopy duration seven days shorter than that of populations from low elevations. Considerable genetic differentiation was observed for senescence timing (range: 9 days), but no significant trend with respect to elevation of origin was observed.

Fig. 1.

Summary of population divergence patterns for the phenological traits leaf unfolding (LU), leaf senescence (LS) and canopy duration (CD), as a function of elevation (in situ, A-C) and elevation of origin (in the common garden, D-E). Regression slopes b (in days/meters above sea level) are shown on each graph, along with their standard error (SE) and the corresponding R². Regressions were estimated with linear mixed-effect models fitted by restricted maximum likelihood methods, with phenology as a response variable and elevation as an explanatory variable. Population, mother (for the common garden only) and individual (repeated measures) were included as random effects. This figure summarizes and updates previous studies of Q. petraea in the Pyrenean elevation gradient system (Vitasse et al., 2009a; Alberto et al., 2011). DOY: date of the year.

This study system therefore provided us with an ideal biological context for investigating multivariate genetic adaptation of the phenological cycle in populations facing extreme environmental changes. However, all these previous studies focused on a single trait. No multivariate study has yet been conducted to explore how genetic constraints drive evolutionary changes to the phenological cycle in oaks. This study based on a highly replicated dataset (multiyear assessments) provides a precise comparison of genetic and environmental variation, and added value due to the exploration of a more integrative approach to analyzing and combining in situ and common garden observations in a multivariate quantitative genetics framework.

We performed an integrative quantitative genetic dissection of the leaf phenological cycle, to address the following questions:

• (1)Which phenological trait is most likely to drive the evolutionary dynamics of the phenological cycle: leaf unfolding, senescence, canopy duration, or a combination of these traits?
• (2)What evolutionary scenario shaped the current distribution of genetic and evolutionary variation along the elevation gradient? In particular, were genetic constraints responsible for the multivariate pattern of population divergence?

Materials and Methods

Natural populations and the common garden experiment

This study was based on a combination of in situ and common-garden designs for simultaneous estimation of the components of genetic differentiation, and of genetic and environmental (within-population) variation in oak populations along a replicated elevation gradient on the northern side of the Pyrenees. The experimental design is described briefly below, and further details about the study sites and the measurement protocols for the assessment of spring and fall leaf phenological traits can be obtained from Alberto et al. (2010; 2011; 2013b), Vitasse et al. (2009a; 2009c) and Appendix S1.

We monitored spring and fall phenological traits in 10 populations from two Pyrenean valleys along an elevation gradient extending from 131 to 1630 m above sea level annually (except for 2008 and 2013), from the spring of 2005 to the fall of 2015. This elevation gradient encompasses the entire elevation distribution of Q. petraea in the Pyrenees.

Open-pollinated acorns from mother trees from the same populations growing in situ were collected in 2006, germinated in greenhouse in 2007 and transplanted in 2008 to a common garden at sea level (Toulenne Research Station, South-East France), with favorable conditions for vegetative development (warm temperatures beginning early in spring and no frost until late fall). We sampled 152 mother trees (mean of 15 mother trees per population; range: 7 - 33). The mean number of offspring per tree was 23.0 (range: 1 - 123). The common garden was flooded in 2010. As a result, some of the trees died and sample size decreased slightly from 2009 to 2015, to 12.1 mother trees per population (range: 2 - 33) and 10.7 offspring per tree (range: 1 - 88).

Leaf unfolding date was assessed over nine (2005-2007, 2009-2012 and 2014-2015) years in situ and seven (2009-2015) years in the common garden. Leaf senescence date was evaluated over seven (2005-2007 and 2009-2012) years in situ and five years (2009 and 2012-2015) in the common garden. Canopy duration and covariation between traits were thus analyzed on the basis of estimates for seven years in situ and five years for the common garden, resulting in estimates of the genetic values more robust than those based on single-year measurements (Alberto et al., 2011). The database used for the analysis has 15659 entries in total (see Supplementary Table 1). Genotypic arrays of 16 microsatellite markers from Alberto et al. (2010) were reanalyzed, to compare differentiation between phenological traits and neutral markers, by comparing Q_ST and F_ST. The genotyping procedure is described in detail in the study by Alberto et al. (2010) and in the supplementary material for this study.

Genetic dissection of the phenological cycle

The evolutionary dynamics of the components of a tree apical bud phenological cycle can be modeled by assuming that the duration of bud extension (or canopy duration, CD) is a composite trait dependent on the timing of bud burst (here, leaf unfolding date, LU) and the timing of bud set (here, leaf senescence, LS). For any individual phenotype i, we have CD_i = LS_i − LU_i. A phenological cycle therefore comprises traits measured on two different types of scale: an interval scale for “timing” traits (i.e. no natural zero point for LU and LS) and a ratio scale for canopy duration (i.e. there is a natural, biologically meaningful, zero point for CD). All three traits may be considered to be subject to selection, but the variance of CD is simply a component of the variance of the two timing traits: σ²(CD) = σ²(LU) + σ²(LS) − 2σ(LU, LS), assuming an absence of bias due to measurement error for LU and LS. It is straightforward to show that the least-square regression slope of CD on LU is b_CD,LU = b_LS,LU − 1, reflecting the fact that our dataset includes three traits but only two dimensions. The variance components of CD can therefore be deduced from the variance components of LU and LS, and it could be argued that the analysis of CD provides no additional information. However, as one of our aims was to compare the distribution of traits potentially subject to selection in our study system, we performed an analogous univariate analysis for CD too. Nevertheless, it should be borne in mind that this trait is not a true third trait, but simply a component of the variation of the two timing traits. Below, we apply the principle of Lande’s (1979) equation to this phenological cycle:

$$\{\begin{array}{c}\Delta \overline{LS}={\sigma }_a^2(LS){\beta }_{LS}+{\sigma }_a(LS,LU){\beta }_{LU}\\ \Delta \overline{LU}={\sigma }_a^2(LU){\beta }_{LU}+{\sigma }_a(LS,LU){\beta }_{LS}\end{array},$$

describing evolutionary change in the two timing traits as a function of their G-matrix elements (additive (co)variances ${\sigma }_a^2$ and σ_a) and the selection gradients (β) exerted on these traits. By estimating G-matrices and comparing them with population divergence patterns (e.g. Schluter, 1996; Hansen & Houle, 2008), we were able to evaluate the influence of genetic correlations on the evolutionary dynamics of the phenological cycle. This analysis was combined with a Q_ST-F_ST approach (Leinonen et al., 2013), to evaluate the role of prior diversifying selection acting on these traits.

Estimation of genetic variances and covariances for combined in situ and common garden assessments

Alberto et al. (2011) found that genetic variance for leaf unfolding date was much smaller for populations at high elevations (more than 1000 m above sea level) than for populations at lower elevations. We therefore replicated all analyses for low- and high-elevation populations separately, with the same partitioning (i.e. three sites per valley for low elevations and two sites per valley for high elevations). Due to the small number of mother trees growing in situ within each population (see Appendix S1), the sample was too small to obtain reliable estimates of G for each population separately. We therefore estimated average G-matrices for the gradient and for the low and high population subsets (Alberto et al., 2011).

An integrative statistical model combining information from both in situ and common garden designs was fitted to the data. The (co)variance of phenological traits in the system was simultaneously partitioned within and between populations, with the following mixed-effect model (in which upper-case letters denote fixed effects and lower-case letters denote random effects):

$$z_{jkmno}=D_j+(D_j)B_k+(D_j){(Bp)}_{km}+(D_j)p_m+a_{jkmn}+d_{jkmn}+{\epsilon }_{jkmno}$$ [1]

where for any trait z, D denotes the fixed effect of experimental design j (i.e. in situ or in the common garden), B is the fixed effect of block k (in the common garden only), p is the random effect of population m, with each of these terms estimated separately within each design (with a block × population term in common garden). The model was fitted and between-population (co)variances were estimated separately within each experiment: in situ and in the common garden. a and d denote breeding value and the non-genetic individual effect of the individual n, respectively, and ε is the within-individual variation, corresponding to between-year replicates o. The d term is the permanent environmental effect (Lynch & Walsh, 1998; Kruuk, 2004), grouping between-year measurements replicated on the same individual; it estimates inter-individual non-genetic effects (e.g. Coltman et al., 2003; Bolstad et al., 2014). The final residuals ε therefore quantify within-individual (co)variance between years. This approach made it possible to compare the level of within-individual variance with other components of population variance. The variance component ${\sigma }_a^2$ estimates the genetic variance in an ‘animal model’ framework (Kruuk, 2004). When applied to a simple open-pollinated offspring design for which parental phenotypic values are available, an animal model accounts for both half-sib and mother-offspring relatedness, making it possible to combine in situ (mother) and common garden (half-sibs) measurements to obtain a better estimate of the trait’s genetic variance ${\sigma }_a^2.$ As in most quantitative genetic studies of forest trees, we were not able to As in most quantitative genetic studies of forest trees, we were not able to disentangle the maternal and the additive genetic effects. However, a parentage analysis-based preliminary study in Q. petraea indicates negligible amount of maternal variance for phenology (Firmat C., Ducousso A., Kremer A., unpublished data). Univariate analyses were carried out for the three phenological traits. A bivariate variance model was estimated for LU and LS. In this analysis we assumed that there was no gene by environment (G×E) interaction. This assumption is supported by preliminary analyses showing an absence of variation in the response of tree genotypes to annual temperature (Soularue J.-P., Firmat C., Ronce O., Caignard T., Delzon S., Kremer A., submitted).

Model [1] was fitted under the Bayesian framework implemented in the MCMCglmm R package (Hadfield, 2010). For the priors of the Bayesian model, we used zero-mean normal distributions with large variances (10⁸) for the fixed effects, half-Cauchy distributions with a scale parameter of 30 (“weakly informative prior distribution”, Gelman, 2006) for the variance components, and inverse-Wishart distributions for the residuals, with a matrix parameter Vcorresponding to a crude guess estimated from the phenotypic variance-covariance matrix, and a parameter n set to 0.002 and 1.002 for the uni- and bivariate situations, respectively (Hadfield, 2010). Parameter estimates were not sensitive to change in the priors. The model was run for 52,000 iterations, including a burn-in of 2000 iterations and a thinning interval of 50 iterations. Autocorrelation coefficients in the Markov chain-Monte Carlo (MCMC) resampling were consistently below 0.10.

At the population level, the model was constructed so as to partition (co)variances separately in situ and in common garden conditions, ${\sigma }_{p-insitu}^2$ and ${\sigma }_{p-common}^2,$ respectively. The former encompass both genetic and environmental sources of differentiation, whereas the latter includes genetic differentiation. Differences between populations in the relationship between LU and LS were estimated from the least squares regression slope of LS on LU: $b_p={\sigma }_p(LU,LS)/{\sigma }_p^2(LU).$ The separate partition of variances made it possible to measure the discrepancy between bivariate genetic and phenotypic population differentiation (due to large-scale environmental effects acting in situ), by calculating b_p−common − b_{p−in situ}.

The genetic correlation between traits was estimated from the bivariate component ${\sigma }_a^2$ in Eq. 1. It provides information about the tightness of genetic integration and the preferential direction of the response to selection. We therefore report both the squared genetic squared correlation coefficient $({\text{R}}_{\text{a}}^2)$ and the genetic regression slope (b_a) of LS on LU. Both ${\text{R}}_{\text{a}}^2$ and b_a can be interpreted within a theoretical context (Houle et al., 2011). In the bivariate case, the genetic R² is directly interpretable as the trait’s conditional evolutionary potential, with the (1 – R²) value giving the proportion of the genetic variance of one trait available to respond to directional selection when evolution of the other trait is fixed by stabilizing selection (Hansen 2003). Lande (1979) pointed out that the genetic regression slope of trait y on trait x equals the trajectory of the evolutionary change on the y-x plane when selection acts only on x. In this case, the observed evolutionary regression (b_p−common) can be compared with the genetic regression predicting the trajectory of evolutionary change expected if selection acts only on LU, as suggested by the previous results summarized in Figure 1.

Using ${\sigma }_a^2,$ the mean component of within-population genetic variation, we estimated the heritability accounting for between-year within-individual plastic variation in the denominator ${\sigma }_{\epsilon }^2$ as $h_{d+\epsilon }^2={\sigma }_a^2/({\sigma }_a^2+{\sigma }_d^2+{\sigma }_{\epsilon }^2),$ with ${\sigma }_d^2$ the permanent environmental effect variance (see equation [1]). The interpretation of heritability measures depends on the terms included in the denominator (Wilson, 2008). $h_{d+\epsilon }^2$ indicates the importance of genetic variance relative to the total phenotypic variance available to a tree for tracking a fitness optimum that fluctuates from year to year. However, this integrative estimate is not comparable to an heritability calculated for a given year, as described by Alberto et al. (2011) for our study system. A comparable measurement can be obtained by excluding the intra-individual variation from the denominator: $h_d^2={\sigma }_a^2/({\sigma }_a^2+{\sigma }_d^2),$ providing a mean estimate of heritabilities calculated for each year separately. Evolvability (Houle, 1992; Hansen et al., 2011) was estimated (in percent) for canopy duration as $e=100\times {\sigma }_a^2(CD)/{\overline{CD}}^2,$ with ${\overline{CD}}^2$ the squared mean of CD.

F_ST-Q_ST comparisons

The divergence patterns of the various traits were compared by considering the Q_ST parameter (for a comprehensive review: Leinonen et al., 2013) calculated as: $Q_{\text{ST}}={\sigma }_{p-common}^2/({\sigma }_{p-common}^2+2{\sigma }_a^2),$ where ${\sigma }_p^2$ is the between-population genetic variance component and ${\sigma }_a^2$ is the mean within-population genetic variance, both estimated from the model in equation [1]. Ovaskainen et al. (2011) suggested a multivariate F_ST-Q_ST comparison method. Here, we needed to analyze CD separately to avoid spurious correlations (due to the two-dimensional nature of our dataset, see above) and LU and LS were mostly uncorrelated (sensu Hansen (2003): genetic R² < 0.05, see Results). We therefore carried out classical univariate Bayesian estimations, the results of which can be interpreted intuitively in this case. The full distribution of MCMC samples was included in each comparison to account for uncertainty in the Q_ST estimates. We used F_ST values estimated from the 16 microsatellite markers studied by Alberto et al. (2010) as the baseline for the evaluation of a stochastic scenario of trait divergence. Two of these markers with differentiation levels suggestive of deviation from neutrality (i.e. high Fst values, Alberto et al., 2010) were not discarded, to provide a conservative test of the hypothesis of directional selection acting on phenological traits (Q_ST > F_ST). As recommended by Whitlock (2008), the Q_ST distribution was compared to the extreme tail of the F_ST distribution: a 95% upper bound was calculated from the mean F_ST assuming a χ² distribution with (n_populations − 1) degrees of freedom, i.e. the Lewontin-Krakauer distribution (Lewontin & Krakauer, 1973; Whitlock, 2008). Locus-specific F_ST values were also estimated, to compare Q_ST estimates with the actual range of genetic differentiation within the genome. All F_ST estimates were replicated for low-elevation, high-elevation and all populations, with the R hierfstat package (Goudet, 2005). Q_ST is generally poorly estimated for small numbers of populations (O'Hara & Merilä, 2005; Whitlock, 2008). This limitation was borne in mind during interpretations of estimates for each population subsets.

Results

Within-population (co)variation

Each phenological trait displayed considerable variation (Table 1), but the genetic variance ${\sigma }_a^2$ of LS was at least twice that for LU. For each trait, most of the variation of the averaged individual phenotypic value was explained by genetic effects, as indicated by the heritability estimates $(h_d^2)$ close to one for each trait. Genetic variance was markedly lower at high elevation than at low elevation (Table 1, Fig. 2): 58% lower for LU, 71% lower for LS, and 45% lower for CD (from values in Table 1). Consistent with these results, the evolvability of CD was 0.05% for low-elevation populations, but fell to 0.03% for high-elevation populations, although this difference was not significant. A very large proportion of the phenotypic variance of the traits (LU: 91%, LS: 87%, CD: 94%) was intra-individual $({\sigma }_{\epsilon }^2).$ This finding reflects the strong plastic variation observed for each of the traits studied, but the individual phenotypic means for each trait were nevertheless largely explained by genetic effects ($0.95<{\text{h}}_{\text{d}}^2<1$ for all traits at the scale of the gradient, Table 1). Accounting for the high within-individual variance in the denominator, heritability $({\text{h}}_{\text{d}+\epsilon }^2)$ fell to between 6% and 13%, but remained different from zero. The environmental variance $({\sigma }_{\epsilon }^2)$ was similar between high- and low-elevation populations for LU, but was markedly higher at low elevations for LS and CD (Table 1).

Table 1. Univariate variance component analysis applied to the three phenological traits and derived statistics.

Traits	Leaf unfolding timing (LU)			Leaf senescence timing (LS)			Canopy duration (CD)
Components	All populations	Low elevation	High elevation	All populations	Low elevation	High elevation	All populations	Low elevation	High elevation
${\mathit{\sigma }}_{\mathit{\text{p}}-\mathit{\text{In}}\mathit{\text{situ}}}^{\mathbf{2}}({\text{day}}^2)$	481.81 (158.19, 1352.49)	212.8 (36.14, 1072.88)	282.7 (19.74, 2546.45)	70.10 (17.69, 205.85)	40.62 (0.12, 221.1)	66.97 (1.46, 973.04)	843.91 (275.63, 2336.86)	537.44 (112.12, 2449.74)	376.94 (29.67, 8450.06)
${\mathit{\sigma }}_{\mathit{\text{p}}-\mathit{\text{Common}}}^{\mathbf{2}}({\text{day}}^2)$	9.01 (3.37, 22.23)	8.07 (1.21, 34.65)	9.76 (1.17, 159.68)	10.85 (3.09, 32.12)	16.67 (0.15, 141.04)	14.17 (0.55, 121.18)	8.95 (1.54, 24.88)	5.79 (0.00, 34.48)	1.92 (0.00, 47.81)
${\mathit{\sigma }}_{\mathit{\text{a}}}^2({\text{day}}^2)$	4.35 (3.78, 4.88)	6.64 (5.48, 7.72)	2.75 (2.21, 3.35)	9.32 (6.93, 11.91)	15.67 (10.56, 21.33)	4.48 (2.6, 6.86)	12.9 (9.67, 16.02)	17.28 (11.15, 23.6)	9.48 (6.71, 13.01)
${\mathit{\sigma }}_{\mathit{\text{d}}}^{\mathbf{2}}({\text{day}}^2)$	0.01 (0.00, 0.09)	0.03 (0.00, 0.27)	0.02 (0.00, 0.14)	0.17 (0.00, 1.43)	0.50 (0.00, 3.61)	0.21 (0.00, 1.63)	0.21 (0.00, 1.61)	0.63 (0.00, 4.32)	0.21 (0.00, 1.55)
${\mathit{\sigma }}_{\mathit{\epsilon }}^{\mathbf{2}}({\text{day}}^2)$	44.21 (43.25, 45.13)	44.42 (42.97, 46.12)	44.00 (42.92, 45.31)	129.68 (125.31, 133.6)	147.79 (140.47, 155.59)	117.53 (112.58, 122.2)	150.48 (146, 155.57)	172.67 (164.38, 183.1)	136.16 (130.00, 141.33)
QST	0.51 (0.30, 0.74)	0.38 (0.12, 0.74)	0.64 (0.32, 1)	0.37 (0.14, 0.64)	0.35 (0.09, 0.86)	0.62 (0.23, 0.98)	0.26 (0.07, 0.51)	0.14 (0.00, 0.51)	0.09 (0.00, 0.72)
${\mathbf{\text{h}}}_{\mathbf{\text{d}}}^{\mathbf{2}}$	1 (0.98, 1.00)	1 (0.96, 1.00)	0.99 (0.95, 1.00)	0.98 (0.86, 1.00)	0.97 (0.78, 1.00)	0.95 (0.69, 1.00)	0.98 (0.89, 1.00)	0.97 (0.78, 1.00)	0.98 (0.85, 1.00)
${\mathit{\text{h}}}_{\mathit{\text{d}}+\mathit{\epsilon }}^{\mathbf{2}}$	0.09 (0.08, 0.10)	0.13 (0.11, 0.15)	0.06 (0.05, 0.07)	0.07 (0.05, 0.08)	0.09 (0.06, 0.13)	0.04 (0.02, 0.06)	0.08 (0.06, 0.10)	0.09 (0.06, 0.12)	0.06 (0.05, 0.09)
e (%)	-	-	-	-	-	-	0.04 (0.03, 0.05)	0.05 (0.03, 0.07)	0.03 (0.02, 0.04)

The variance components p, a, d and ε quantify variation at the between-population (in situ and in common garden conditions), genetic, individual non-genetic and within-individual (environmental) levels, respectively, see the Methods section (equation [1]). The 95% credible intervals are indicated in brackets. See the Methods section for a description of Q_ST, heritabilities ${\mathit{\text{h}}}_{\mathit{\text{d}}}^{\mathbf{2}}$ and ${\mathit{\text{h}}}_{\mathit{\text{d}}+\mathit{\epsilon }}^{\mathbf{2}}$, and evolvability (e) estimates. The CD values used for computing e were 186.21, 187.00 and 183.57 days for all populations, low elevation and high elevation subsets, respectively. Q_ST values for subsets of populations (low- and high-elevation populations) were computed from ${\mathit{\sigma }}_{\mathit{\text{p}}-\mathit{\text{Common}}}^{\mathbf{2}}$ and ${\mathit{\sigma }}_{\mathit{\text{a}}}^{\mathbf{2}}$ estimated separately for each of these two population subsets.

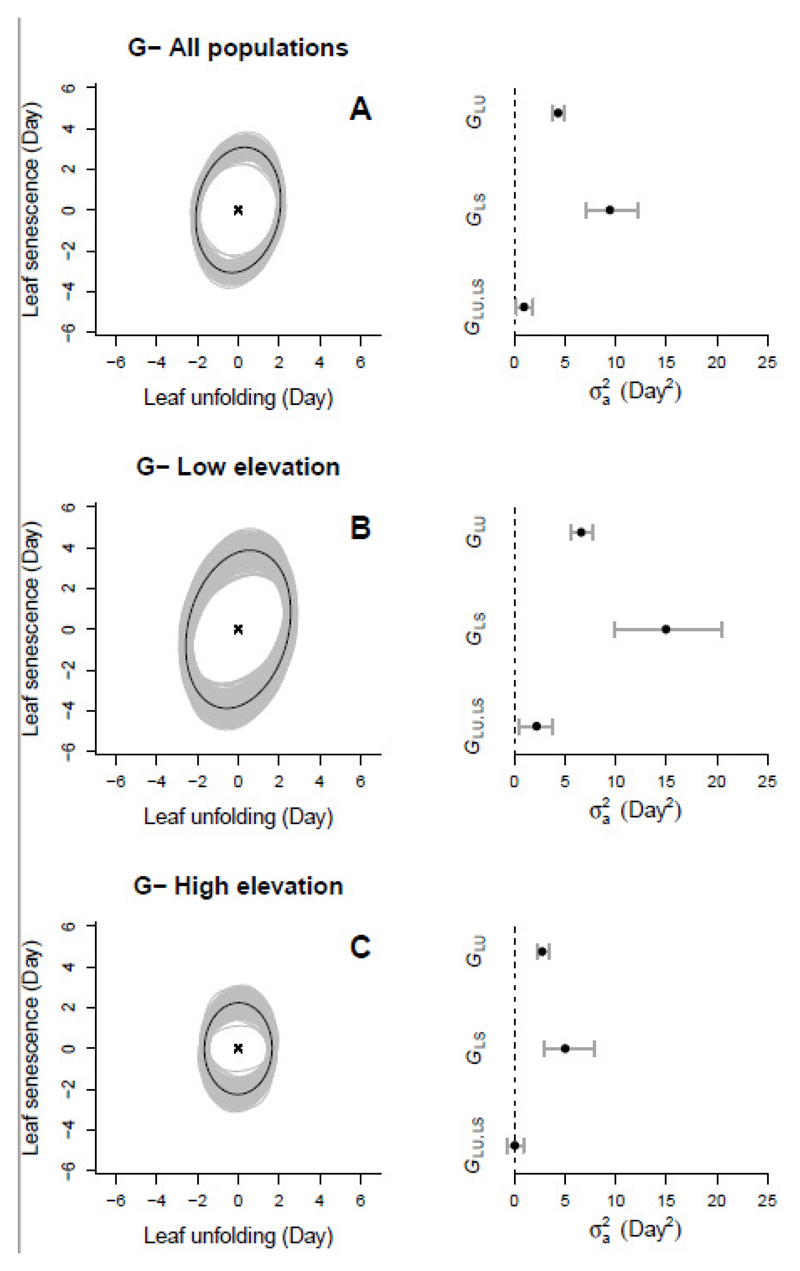
Fig. 2.

Patterns of genetic variance and covariance for the two timing traits: leaf unfolding and (LU) and leaf senescence (LS) dates estimated for different sets of populations: all populations (A), and populations at low (< 1000 m, B) and high (> 1000 m, C) elevations. Left panels: Bivariate representation of the estimated G-matrices (black ellipse) and the corresponding posterior distribution (gray ellipse). The ellipses represent the distribution of the bivariate breeding values centered on zero. Right panels: the same information represented as (co)variance estimates (black dots) and their 95% posterior credible intervals (gray segments).

The estimated G-matrices for LU and LS suggested that there was no close genetic relationship between these traits (Fig. 2, Table 2). The genetic ${\text{R}}_{\text{a}}^2,$ which estimates the trait’s evolutionary potential conditioned by the variance of the other trait (see Methods), did not exceed 5% for any of the sets of populations. Thus, almost all the variance for a particular trait (i.e. at least 95%) remained available when the other trait was subject to stabilizing selection. The slope of the genetic regression line (b_a) for LS on LU was therefore shallow (Fig. 2, Table 2), indicating an absence of strong correlated response to selection on one trait when directional selection acts on the other. However, the genetic relationship between these traits, although very weak for the full set of populations and for those at low-elevation sites (${\text{R}}_{\text{a}}^2=0.02\text{and}0.05,$ respectively, Table 2), was non-zero and positive, indicating a weak genetic relationship between phenological traits. With the marked decrease in the variance of each trait at higher elevations, their genetic covariance σ_a(LS, LU) reached zero (Fig. 2 C, Table 2).

Table 2. Bivariate variance component analysis applied to the timing of leaf unfolding (LU) and leaf senescence (LS), and derived statistics. For each component, the first line indicates the least squares regression slope b and the second line, the R² of the relationship as an estimate of the conditional variance of the traits (see Hansen 2003).

Components	All populations	Low elevation	High elevation
bp−ln situ*	-0.30 (-0.48, -0.09) 0.64 (0.12, 0.97)	-0.29 (-0.84, 0.08) 0.41 (0, 0.89)	-0.11 (-1, 0.71) 0.18 (0, 0.79)
bp−Common	0.45 (-0.29, 1.07) 0.22 (0, 0.64)	0.65 (-0.61, 1.85) 0.27 (0, 0.81)	0.47 (-1.36, 2.58) 0.28 (0, 0.85)
Contrast bp †	0.74 (0.01, 1.42)	0.96 (-0.35, 2.07)	0.65 (-1.25, 2.98)
ba	0.22 (0.04, 0.43) 0.02 (0, 0.07)	0.33 (0.08, 0.55) 0.05 (0, 0.12)	0.02 (-0.24, 0.33) 0.01 (0, 0.05)
bd	0.03 (-20.93, 20.11) 0.07 (0, 0.46)	-0.03 (-18.17, 27.29) 0.16 (0, 0.75)	0.12 (-19.03, 20.76) 0.16 (0, 0.78)
bε	0.25 (0.21, 0.29) 0.02 (0.02, 0.03)	0.22 (0.16, 0.29) 0.01 (0.01, 0.02)	0.27 (0.22, 0.32) 0.03 (0.02, 0.04)

^*Each slope estimate corresponds to b = σ(LU, LS)/σ²(LU), with the indices p, a, d and ε denoting the regression slopes estimated at the between-population (for in situ and common garden experimental designs), genetic, individual non-genetic and within-individual levels, respectively, see the Methods section (equation [1]). 95% credible intervals for b and R² are indicated in brackets.

^†Contrast b_p is calculated as follows: b_p–Common garden – b_p–ln situ.

Regression slopes were estimated for each bivariate variance component of Eq. 1, but the error term of the model $({\sigma }_{\epsilon }^2)$ was the only term yielding a non-zero estimated slope in each case (Table 2). Thus, the two traits display positive environmental covariance σ_ε(LS, LU),, but this covariance accounts for only a small proportion of the variance in the correlated trait (LS) at this level, with all ${\text{R}}_{\epsilon }^2$ values below 3%. The total phenotypic correlation within populations, including the within-individual term, was also positive and very low $({\text{R}}_{\text{a}+\text{d}+\epsilon }^2=0.023[0.000,0.065]).$

Between-population (co)variation

All traits displayed considerable between-population differentiation both in situ and in common garden conditions, with credible intervals excluding zero (Table 1). Only common garden estimates for between-population variance in canopy duration at low and high elevation were not significantly different from zero. Between-population variance is generally much lower in common gardens than in situ (Table 1, Fig. 3), highlighting a strong effect on environment on population phenotypic divergence (Table 1, Fig. 3).

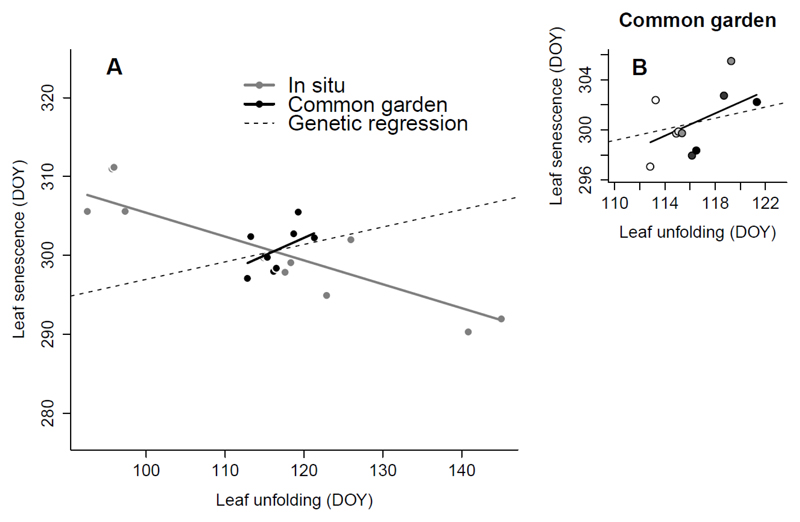
Fig. 3.

Bivariate population divergence between the timing of leaf unfolding (LU) and the timing of leaf senescence (LS). The within-population genetic regression slope (dashed line) is provided for comparison (b_a = 0.22, R² = 0.02). A. This figure illustrates the range of variation and the substantial difference between the phenotypic (in situ, negative: b_p = -0.30, R² = 0.63) and genetic (common garden, positive: b_p = 0.45, R² = 0.22) regression slopes for between-population bivariate divergence (see Table 2). B. Focus on the population (co)variation in the common garden. The darkness of the dots is proportional to the elevation at the original sampling site (range: 131-1630 m). Population estimates are the best linear unbiased predictors (BLUBs) for populations estimated with a mixed-effect model. DOY: day of the year (number of days since January 1^st).

A strongly negative relationship between LU and LS was observed for in situ conditions (Fig. 3). By contrast, a positive relationship was observed for the much narrower range of populations grown in common-garden conditions (Fig. 3), but its credible interval was not distinct from zero (b_p-common = 0.45 [-0.29, 1.07], R² = 0.22). However, the difference between the two slopes was significant (b_p-common - b_{p-in situ} = 0.74 [0.01, 1.42], Table 2).The slope of the within-population genetic regression line (b_a = 0.22 [0.04, 0.43], Fig. 3, Table 2) was shallower than that for genetic divergence between populations (b_p-common). Together with the weak intra-population genetic correlation mentioned above, this finding supports the hypothesis that selection on LU alone is unlikely to have generated the observed pattern of LS divergence.

F_ST-Q_ST comparisons

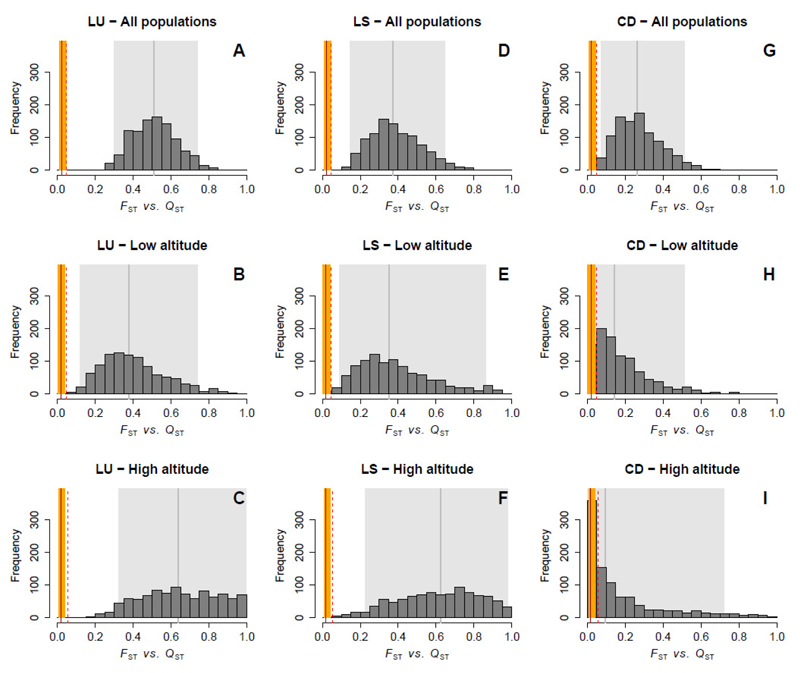
The F_ST values were about 2-3% (Fig. 4) and were reliably estimated, as indicated by the narrow bootstrap-based confidence interval obtained for each set of populations: F_ST = 0.026 (95% confidence interval based on 500 bootstrap replicates: 0.021, 0.031) for all populations, F_ST = 0.022 (0.017, 0.027) for populations at low elevation and F_ST = 0.026 (0.021, 0.033) for populations at high elevation. The 95% upper bound (extreme tail) of the F_ST distribution, assuming a Lewontin-Krakauer distribution, was 0.047 for all populations, 0.046 for low-elevation populations, and 0.055 for high-elevation populations.

Fig. 4.

Q_ST-F_ST comparisons for each phenological trait: leaf unfolding (A-C), and leaf senescence (D-F) dates, and canopy duration (G-I). The analysis is replicated for all populations (upper row) and for populations at low (< 1000 m, middle row) and high (> 1000 m, lower row) elevations. The continuous vertical red line and its surrounding orange area indicate the mean F_ST value for the corresponding set of populations and its range of variation over the 16 microsatellite loci, respectively. The dotted vertical red line represents the 95% upper bound of the confidence interval of a Lewontin-Krakauer distribution estimated for the same loci. The histogram shows the Bayesian posterior distribution (1000 samples) for Q_ST. The vertical gray bar is the median Q_ST and the shaded area is the 95% credible interval obtained from this posterior distribution (see Table 1).

There was evidence for a strong pattern of non-neutral differentiation for LU, with high Q_ST estimates, ranging from 38 to 64%, with the lower limit of the 95% credible interval (CrI) always exceeding the extreme tail of the neutral (F_ST) expectation for each subset of populations (Fig. 4 A-C, Table 1). A similar but less clear pattern was observed for LS, with Q_ST estimates ranging from 35 to 62% (Fig. 4 D-F, Table 1). The 95% CrIs of Q_ST systematically excluded the extreme tail of the F_ST distribution. A different pattern was obtained for CD (Fig.4 G-I), with Q_ST values ranging from 9 to 26%. In this case, the upper tail of the F_ST distribution was included within the 95% CrIs of Q_ST for populations at low and high elevations. However, for the full set of populations, the 95% CIs of Q_ST excluded the neutral expectation, suggesting that this trait was subject to directional selection.

The between-population variance component was systematically slightly lower for CD than for the other traits and the CrI included zero (Table 1). These lower Q_ST values were, therefore, not merely a consequence of the particularly high level of within-population genetic variance estimated for this trait. They also resulted from weaker between-population differentiation for CD than for the other traits. Thus, on the basis of Q_ST -F_ST comparisons, scenarios involving strong directional selection across the elevation gradient seem less likely for CD than for the two timing traits, LU and LS.

Discussion

Phenological traits are known to be extremely plastic in trees (e.g. Vitasse et al., 2010) and phenotypic values can therefore fluctuate strongly from year to year, affecting estimates of genetic parameters. Here, each estimate was based on at least five measurements per tree, replicated across years, providing a unique opportunity to obtain more realistic averaged breeding and phenotypic values, together with population averages. Thanks to the high degree of replication in this dataset, we were also able to evaluate environmental variation and compare it with genetic variation. By performing an overall dissection of the phenological cycle and assessing these traits in situ and in a common garden, we were able to identify the target traits involved in local adaptation and driving the evolutionary dynamics of the phenological cycle.

Targets of selection

The genetic divergence of quantitative traits (Q_ST) markedly exceeded neutral expectations (F_ST) at all elevations, for both leaf unfolding (LU) and leaf senescence (LS) dates. For canopy duration (CD), the pattern was less clear, as the credible intervals for Q_ST values for low and high elevations included the F_ST. This discrepancy may reflect the lack of statistical precision for Q_ST estimates obtained for a small number of populations (O'Hara & Merilä, 2005; Whitlock, 2008). However, we cannot exclude the possibility that this trait was subject to a lower level of directional selection than the other two traits as Q_ST ≫ F_ST for LU and LS for the same subset of populations, and Q_ST was lower for CD than for LU and LS when the full set of populations was analyzed. CD may display a lower level of differentiation due to partial compensation for the two traits, with a temporal displacement of the growing season. Thus, a positive offset in the response of LU to selection for an advanced flushing date may have led to a positive response for LS (positive evolutionary covariation in the common garden), leading to a pattern more closely resembling stabilizing selection for CD and a buffering of the decrease in CD. This scenario is consistent with the weak but positive relationship between the mean genetic values of the two traits across populations. A clear Q_ST ≫ F_ST pattern was recently reported for fall phenology in Populus angustifolia but not for other phenological traits (Evans et al., 2016). Thus depending on the species, timing traits (either LU or LS) appear to be more strongly targeted by selection than CD.

In summary, both timing traits considered here have been exposed to divergent selection associated with local adaption to elevation, with LU possibly subject to stronger selection than LS. Different abiotic and biotic drivers of directional selection on LU in oaks have been identified. Evolutionary changes in LU may have enabled the trees to avoid early frosts (Dantec et al., 2015). Responses to biotic pressures may also trigger changes in LU, as shifts in LU have been shown to enable plants to avoid insect herbivory (Crawley & Akhteruzzaman, 1988; Tikkanen & Julkunen-Tiitto, 2003; Wesołowskia & Rowińskib, 2008). Finally, pathogens displaying population expansions during the oak flushing period, such as the powdery mildew fungus, are likely to alter the timing of leaf unfolding (Desprez-Loustau et al., 2010; Dantec et al., 2015).

Canopy duration is correlated with annual carbon intake and, thus, growth, a crucial trait for juvenile tree fitness in a context of harsh competition for light. Growth was shown to decrease substantially with increasing elevation of provenance in a study with a similar experimental design (Vitasse et al., 2009a), consistent with the decrease in CD with increasing elevation reported here. This slower growth of high-elevation populations, with a shorter CD in optimal common garden conditions, is consistent with a fitness cost of CD reduction. LS may thus have evolved to compensate, at least in part, for the delay in leaf unfolding in spring. The fitness cost of flushing occurring to early may be substantial, due to frost damage. The cost of senescence occurring “too late” is probably smaller. However, early frosts in the fall may induce leaf abscission, impairing the resorption of nitrogen and carbon (Norby et al., 2003). However, a “risk-taking” genotype with a long CD at high elevation might be at an advantage in terms of its greater ability to fix carbon during the most favorable years (first frosts in the late fall), compensating for incomplete nutrient resorption in the least favorable years (first frosts in the early fall). However, the problem is actually more complex, due to differences in photoperiod and photosynthetic capacity between the spring and the fall. Thus, an additional day of CD in the fall cannot necessarily compensate for the loss of a single day in the spring (see Vitasse et al., 2010; Bauerle et al., 2012 and references therein). This may account for the stronger selection on spring phenology observed here.

Most (about 90%) phenological variation is expressed at the within-individual level (referred to as ‘environmental variability’ hereafter). For instance, only two environmental standard deviations for LU (i.e. 2×√44 = 13 days, taking the residual variance estimate from Table 1) encompass 25% of the large-scale in situ phenotypic differentiation (about 52 days, Figure 1, i.e. 13/52 = 0.25): the within-individual variation was therefore considerable relative to large-scale phenotypic differentiation. If this environmental source of variability contributes to the short-term maintenance of fitness in a changing environment (Merilä, 2012), then it might explain the much weaker genetic differentiation in common garden conditions than in situ. A recent comparative analysis (Tansey et al., 2017) provided support for this hypothesis: adaptive plasticity for spring phenology in plants (including Q. petraea) was found to be common and to allow populations to track their thermal optima.

This strong environmental variability paradoxically contrasts with the high heritability commonly reported for phenological traits in trees (Howe et al., 2003). This paradox can be explained simply by the fact that most studies include measurements for only one year or analyze several years of data independently (e.g. Alberto et al., 2011): this is illustrated by the contrast we found between our two estimates of heritability (accounting for environmental variability in the denominator and not accounting for this variability, ${\text{h}}_{\text{d}+\epsilon }^2$ and ${\text{h}}_{\text{d}}^2,$ respectively). For future quantitative genetic studies in plant populations, we would recommend quantifying, whenever possible, environmental (within-individual) variability and comparing it with genetic variability. One appropriate strategy would be the introduction of a permanent environmental effect into the model, as in this study.

Patterns of population divergence

The positive evolutionary relationship between the two traits was weakly supported due to the narrow range of variation in common garden conditions, but both LU and LS displayed strong between-population differentiation. This suggests that local adaptation to elevation involves both spring and fall phenology, and is therefore dependent on the full phenological cycle of the apical buds. Temperature may contribute to the genetic codivergence of these traits in Q. petraea, as LU and LS are both negatively correlated with temperature at the site of origin (Vitasse et al., 2009a).

Given the almost total absence of a genetic correlation between these traits, the hypothesis that evolutionary variation in one trait (e.g. LS) was generated by directional selection on the other (e.g. LU) can be definitively ruled out: no correlated response would be expected from such a weak genetic correlation. Even with a much closer genetic relationship, Lande’s (1979) equation predicts that a one-day offset in LU due to selection on this trait alone would imply an expected correlated LS response of only 0.22. An evolutionary slope twice as high as that actually observed (b_LU,LS = 0.45, see Fig. 3) is therefore incompatible with the scenario of a strictly correlated response for LS. Thus, some degree of divergent selection on LS has probably contributed to the evolution of the phenological cycle to cope with the harsh conditions at high elevation. Genetic correlations are often expected to slow the rate of adaptation and range expansion (e.g. Etterson & Shaw, 2001; Duputié et al., 2012), but this does not appear to be the case for leaf phenology in sessile oak in the Pyrenees. These results corroborate the long-standing assumption that spring phenology is the primary trait affected by climate-mediated selection. Nevertheless, the similar, albeit probably weaker, divergence observed for LS suggests that greater attention should be paid to the role of fall phenology in the long-term adaptation of trees to a changing climate (e.g. Gill et al., 2015; Xie et al., 2015).

Inversion of the between-population correlation

A surprising finding of this study was the different sign of the between-populations correlation between the two timing traits: the correlation coefficient was positive for the common garden and negative when estimated in situ. The strong inverse correlation in situ is therefore entirely driven by environmental effects, i.e. the large-scale in situ climatic conditions related to elevation. In situ, a delay of one day in LU would lead to an expected change in LS of 0.30 days. In the common garden, a delay of one day in LU would lead to a change in LS date of +0.45 days. This difference is substantial, as indicated by a comparison of the two slopes (Table 2, Fig. 3). Population covariation in common garden conditions is assumed to be of purely genetic origin. Taking this covariation as a reference, this implies that, at the scale of the elevational gradient, one or several environmental factors act on the two traits to generate this strong negative covariation. This suggests that the environmental effects on LU and LS at the elevational scale (metapopulation level) act in opposite directions (Pélabon et al., 2013 for a detailled graphical model). However, when the environmental correlation between the traits was measured over a temporal scale (i.e. within individual trees from the replicated interannual measurements, by the ultimate error term of the equation [1], see Methods), a positive correlation was found. This indicates that reaction norms over time (interannual within-site variation) are of the same sign. This may be beneficial for tree fitness, as it may make it possible to compensate in the fall for a canopy duration shortened by cold temperatures in the spring. This study therefore sheds light on two distinct patterns of environmental covariation between phenological traits.

In cold years, the later establishment of the canopy in the spring may be compensated plastically by a later shedding of the canopy in the fall, but this pattern does not hold at the scale of the elevation gradient, which includes harsh climatic conditions: the negative covariance is the expression of macro-environmental constraints that translate into a shorter canopy duration at high elevation. At this macro-environmental level, plasticity may be “passive” and non-adaptive in nature (Westneat et al., 2015), being mostly driven by purely physical processes that vary over the gradient, such as spring temperature or leaf abscission due to early frosts in the fall.

Evolution of genetic (co)variances: causes and consequences

A spectacular erosion of about 50% of the genetic variance along the elevation gradient has been reported for LU (Alberto et al., 2011). We observed a similar pattern for LS and CD. The evolutionary potential of the entire phenological cycle therefore decreased with adaptation to high elevation. Evolvability, a standardized measurement of evolutionary potential (Hansen et al., 2011), can be calculated for CD only, and was found to be 40% lower at high elevation than at low elevation. However, this large decrease in evolvability would be unlikely to slow local adaptation to the point of jeopardizing population survival. First, the evolvability of CD, even at high elevation (e = 0.03%), remained within the range of evolvabilities capable of producing a substantial change in the trait mean over a limited number of generations under average selection intensity (Hansen et al., 2011). Furthermore, the almost total absence of genetic correlation between traits results in almost all (here, more than 95%) the variation of one trait being available to respond to selection if the other trait is fixed by stabilizing selection. In addition, substantial amounts of genetic variation can be maintained by long-distance gene flow in trees (Kremer et al., 2012; 2014).

Finally, correlated selection is thought to align the major axis of the G-matrix (Schluter (1996)’s “g-max”) with the main features of the adaptive landscape, thus influencing the pattern of genetic variation, as predicted by theoretical models (Arnold et al., 2008; Pavlicev et al., 2010; Jones et al., 2014). However, it remains unclear how much the major axis of G can be altered by selection in natura (e.g. Roff & Fairbairn, 2012; Firmat et al., 2014; Teplitsky et al., 2014a), as there are too few empirical data to support or refute this hypothesis. As discussed above, the adaptation to high elevation in our study system probably resulted from positive directional selection on the two timing traits. Theoretically, G would therefore be predicted to be aligned with the direction of bivariate divergence (i.e. a positive genetic correlation would appear). However, the between-trait genetic relationship did not evolve to match the main vector of population divergence. Instead, genetic covariation tended to vanish. This suggests that the orientation of G may be robust to the influence of strong directional selection. Finally, canopy duration, as a compound trait, can evolve only through changes in LU and/or LS. Its expected capacity to respond to selection is given by ${\sigma }_a^2(CD)={\sigma }_a^2(LU)+{\sigma }_a^2(LS)-2{\sigma }_a(LU,LS):$ the evolutionary potential of CD is decreased by a strong positive genetic covariance between the traits. Thus, as CD is a trait determining growth rate and, thus, fitness (see above), we cannot exclude the possibility that selection favors a genetic decoupling of LU and LS. For example, in a global warming context, the optimum LU would occur earlier (i.e., negative selection differential. For Q. petraea see Vitasse et al., 2009b) and the optimum LS would occur later (i.e., positive selection differential). The weak positive genetic correlation found between these traits would not be expected to impose constraints on the evolutionary response to negative correlative selection induced by a warming of the climate.

Concluding remarks and summary

We describe here the first integrated evolutionary quantitative genetic dissection of a full leaf phenological cycle for yearly tree growth. Our results confirm that the timing of leaf unfolding is a critical trait for local adaptation but that leaf senescence is also involved, although its relationship to elevation remains unclear. Adaptation to a broad range of climatic conditions probably involves correlative selection on leaf senescence timing to maximize canopy duration in extreme environments. We found that spring and fall traits displayed only very weak genetic integration and were, therefore, free to evolve independently of each other. Given the weak genetic integration of phenological traits, their high levels of genetic variation and their impressive environmental variability, our results suggest that phenological evolution will not be a limiting component of short-term adaptation to global warming in sessile oak.

Supplementary Material

Additional Supporting Information may be found online in the supporting information tab for this article:

Appendix S1. Supplementary Methods section: Details of the study sites and the Toulenne common garden design – Methods for the assessment of phenological traits.