Abstract
The false positive rates (FPR) for surface-based group analysis of cortical thickness, surface area, and volume were evaluated for parametric and non-parametric clusterwise correction for multiple comparisons for a range of smoothing levels and cluster-forming thresholds (CFT) using real data under group assignments that should not yield significant results. For whole cortical surface analysis, thickness showed modest inflation in parametric FPRs above the nominal level (10% versus 5%). Surface area and volume FPRs were much higher (20–30%). In the analysis of interhemispheric thickness asymmetries, FPRs were well controlled by parametric correction, but FPRs for surface area and volume asymmetries were still inflated. In all cases, non-parametric permutation adequately controlled the FPRs. It was found that inflated parametric FPRs were caused by violations in the parametric assumptions, namely a heavier-than-Gaussian spatial correlation. The non-Gaussian spatial correlation originates from anatomical features unique to individuals (e.g., a patch of cortex slightly thicker or thinner than average) and is not a by-product of scanning or processing. Thickness performed better than surface area and volume because thickness does not require a Jacobian correction.
Introduction
Doing science is like solving a jigsaw puzzle where each piece is a conclusion from a study. However, unlike a real jigsaw puzzle, not all the pieces are correct. The more incorrect pieces, the harder it is to assemble them into a big picture, so controlling the fraction of wrong pieces is important. Scientific journals generally require that authors compute the probability that their positive conclusions could arise under the null hypothesis (the false positive rate, FPR) and generally (and arbitrarily) require that this probability be less than 5% for publication (Benjamin et al., 2017). In the field of neuroimaging, the computation of the FPR is complicated by the fact there are tens of thousands of measurements (voxels) in an image of the brain. Since it is not generally known where an effect of interest will occur, an FPR is usually computed separately for each voxel (so-called “mass-univariate analysis”). These univariate FPRs must then be corrected for tests across multiple voxels to compute a final FPR for the conclusion of the study (also known as the family-wise error rate (FWE)). This is the problem of multiple comparisons.
Several techniques exist to solve the multiple comparisons problem. Historically, random field theory (RFT, Worsley et al., 1992; Friston et al., 1994; Forman et al., 1995) has been a very popular solution for fMRI (Carp, 2012). RFT is a parametric method that that corrects for multiple comparisons using either the maximum statistic or statistics derived from clusters of spatially connected voxels. For the clusterwise analysis, the image is reduced to sets of contiguous voxels (clusters) whose univariate p-values are more significant than some (arbitrarily-defined) cluster-forming threshold (CFT). The final FPR is then the probability of seeing a cluster of that size by chance. Clusterwise RFT correction requires that the CFT and smoothing levels be high; violations of this requirement result in conservative FPRs (Friston et al., 1994; Hayasaka et al., 2003). Monte Carlo (MC) simulations can be used to overcome these requirements (Hayasaka et al., 2003). In MC simulation, white noise is smoothed and thresholded and then clusters extracted; after many iterations, the distribution of cluster sizes under the null is determined and used to compute the p-value of the clusters in the real data. While MC simulations avoid constraints on the CFT and level of smoothness, they are still parametric in the sense that there are still assumptions on the shape of the smoothing kernel (usually Gaussian) and that the underlying noise is Gaussian distributed. RFT, MC, and permutation generally assume that the smoothness itself is constant across the image (i.e., spatial stationarity), though methods exist to relax this assumption (see Discussion).
Concern about controlling false positives in neuroimaging has grown recently. Eklund et al., 2016, ran tests on resting state fMRI data analyzed as task and found that the p-values generated by both RFT and MC simulation clusterwise correction were between 10 and 60%, far exceeding the nominal 5% level (Woo et al., 2014, found a similar effect). This raised the possibility that the conclusions from many published fMRI studies are partially or entirely incorrect. The RFT FPRs were brought into line by using a higher CFT and smoothing levels. Eklund, et al, 2016, concluded that the source of the problem was that a key assumption of both RFT and MC was not being met, namely that the data did not have Gaussian spatial smoothness. Cox et al., 2017 also came to the same conclusion. Non-Gaussian spatial smoothness has been noticed in fMRI before (Kriegeskorte et al., 2008). Eklund, et al, 2016, found that, in most cases, permutation (Nichols et al., 2001; Winkler et al., 2014) gave adequate control of FPRs. Elevated FPRs can be mitigated slightly by sampling into a lower resolution group space (Flandin et al., 2016; Mueller et al., 2017).
The Eklund and Woo results are limited to fMRI brain imaging. A few papers have addressed morphological analysis using voxel-based morphometry (VBM, Ashburner et al., 2000). Silver et al., 2011, found highly elevated FPRs, in the range of 10–50%, when using RFT cluster correction; permutation resulted in well-controlled FPRs. Scarpazza et al., 2013, found inflated FPRs when a single subject was compared to a group using RFT cluster correction; a subsequent analysis (Scarpazza et al., 2016) showed that permutation-based cluster correction had adequate FPR control. Scarpazza et al., 2015 and Meyer-Lindenberg et al., 2008 found that RFT adequately controls FPRs in when the maximum statistic is used, though Salmond et al., 2002, found elevated FPRs unless the smoothing level was greater than 8mm FWHM.
Surface-based analysis is an alternative to VBM for morphological analysis. In Surface-based analysis, the cerebral cortex is modeled as a 2D sheet from which thickness, surface area, and volume can be computed at each point. These quantities can be analyzed in a group surface space after surface-based registration and surface-based smoothing. Thousands of surface-based studies have been performed, mainly using FreeSurfer1 (www.freesurfer.net) with clusterwise correction computed with parametric Gaussian-based MC simulations to compute the FPR2. In this manuscript, we evaluate the validity of FPRs computed in this way using real data analyzed in FreeSurfer.
Methods
the data sets used in this study came from the 1000 Functional Connectomes data base (1000 Functional Connectomes, fcon_1000.projects.nitrc.org/fcpClassic/FcpTable.html). This is a public data base of anonymized data. The data were collected according to procedures approved by the local ethics board at each site. The institutional review boards of NYU Langone Medical Center and New Jersey Medical School approved the receipt and dissemination of the data (Biswal et al., 2010). While best known for fMRI, the 1000 Functional Connectomes also has anatomical MRI data from which we analyzed 499 subjects. The set of subjects was identical to that used in Eklund et al., 2016: Beijing (198 subjects), Cambridge (198 subjects), and Oulu (103 subjects), all at 3T. The subjects ranged in age from 18–30y. The voxel size was Beijing: 1.3×1×1mm, Cambridge: 1.2×1.2×1.2mm, Oulu: .94×.94×1mm.
All subjects were analyzed in FreeSurfer (www.surfer.nmr.mgh.harvard.edu) to provide detailed anatomical information customized for each subject (Dale et al., 1999; Fischl et al., 1999a). Version 5.3 was used for most of the analysis, but the Oulu data was also analyzed in Version 6.0 to gauge consistency. The FreeSurfer analysis stream includes intensity bias field removal, skull stripping, and assigning a neuroanatomical label (e.g., hippocampus, amygdala, etc.) to each voxel (Fischl et al., 2002; Segonne et al., 2004). In addition to the volume-based analysis, FreeSurfer constructs models of the cortical surface. A surface model consists of a mesh of triangles. The location of the mesh is controlled by adjusting the location of the vertices. A vertex is the place where the points of neighboring triangles meet (typically about 1mm apart). The vertex positions are adjusted such that the surface follows the T1 intensity gradient between cortical white matter (WM) and cortical gray matter (GM). Smoothness constraints allow the surface to cut through a voxel to model partial volume effects and provide subvoxel accuracy of the location of the surface. A second surface is also fit to the outside of the brain (between the GM and the pia). The first surface is called the “white” surface, and the second is called the “pial” surface. The left hemisphere (LH) and right hemisphere (RH) are modeled separately. All surfaces are constructed in the individual anatomical space.
The distance between the white and pial surfaces at a vertex is defined to be the cortical thickness at that vertex (Fischl et al., 2000). The thickness at a vertex is computed as the average of two distances. The first is the distance from the white surface vertex to the closest point on the pial surface (not necessarily at a pial vertex); the second is the distance from the corresponding pial vertex to the closest point on the white surface (again, not necessarily at a vertex). The area of a vertex is defined as the average area of the triangles of which the vertex is a member. The GM volume3 of a vertex is defined as the area times the thickness4. The surface curvature5 at a vertex can be computed based on its spatial relationship to neighboring vertices. The curvature is a quantification of the geometry of the folding patterns. Thus, at each point along the subject’s surface, the thickness, area, volume, and curvature can be quantified, all with subvoxel accuracy.
The folding pattern quantification is used to drive a non-linear surface-based inter-subject registration procedure that aligns the cortical folding patterns of each subject to a standard surface space (Fischl et al., 1999b). This approach is similar to performing a volume-based registration to Talairach or MNI space but is significantly more accurate for cortical areas (Fischl et al., 2008; Klein et al., 2010) and uses geometry instead of voxel intensity. The registration minimizes two competing terms: (1) the difference between the atlas geometry and the individual geometry and (2) the local metric distortion (i.e., how much the surface must be stretched or compressed from the original to match the atlas). The registration is performed in spherical space, i.e., the atlas exists as a sphere (a 7th order icosahedron). First, the subject’s white surface is “inflated” to the shape of a sphere, and the geometry quantification of the white surface is transferred to the sphere. The location of the vertices on the sphere are then adjusted to minimize the overall cost described above to establish the correspondence.
The surface registration is applied in one of two ways depending upon whether the total quantity being mapped needs to be conserved (e.g., area, volume) or not (e.g., thickness, fMRI, PET). In both cases, the target atlas is a surface (“fsaverage”) with 163,842 vertices (individuals tend to have about 120,000 vertices). In the non-conserving case, for each target vertex, the closest source vertex in the individual’s spherical surface is found. The value of the quantity to be mapped (e.g., thickness) is then assigned from the individual’s vertex to the target vertex thus assigning each target vertex a value. If a given source vertex maps to multiple targets, then its value is simply replicated at each target. There is the possibility that some vertices from the individual are never the closest to any target vertex and so are not represented in the output. To account for this, we reverse the processes, going through each unrepresented source vertex and mapping it to the closest target vertex. If a target vertex receives multiple source vertices, the value at the target is the average of the sources.
In the quantity-conserving case, the method is the same but with adjustments to preserve the total value. When there are multiple target vertices for a single source vertex, the value assigned to each target is set to the source value divided by the number of targets (rather than replication). When multiple source vertices map to a single target vertex, the value at the target is set to the sum (rather than the average) of the sources. These adjustments can be thought of as a “Jacobian correction” (similar to that described in Winkler et al., 2012) to account for local stretching or compression in the registration. After these modifications, the sum of the values of the vertices in the target is equal to that in the source. This is important for area and volume because we do not want the total quantity to change. This correction is not needed for thickness because it is measured along a vector normal to any stretching or compression. For volume and surface area maps, the values are divided by an estimate of total intracranial volume (eTIV, Buckner et al., 2004) for each subject; this is done to account for differences in volume and surface area purely due to differences in head size.
Smoothing is applied after resampling into the target space. This process is repeated for each subject after which their maps can be concatenated into a stack ready for vertexwise analysis. Spatial smoothing on the surface in FreeSurfer is implemented using iterative nearest neighbor averaging. This is an approximation to Gaussian smoothing where the number of iterations is related to the desired full-width/half-max (FWHM).
A laterality analysis was also performed using the tools described in Greve et al., 2013. The laterality analysis looks for cortical asymmetries in thickness, area, and volume (e.g., language areas have strong anatomical differences between left and right hemispheres (Keller et al., 2011)). In the asymmetry analysis, the left and right hemispheres were surface-registered to a symmetric atlas. After spatial smoothing, a laterality index (LI) was computed at each vertex as LI = (L−R)/(L+R), where L is the value at a vertex in the left hemisphere and R is the value at the homologous vertex in the right hemisphere. The laterality analysis is being performed to document the performance for the evaluation of previously published studies that have used this method and to also help elucidate the source of false positives more generally.
Following Eklund et al., 2016, 20 or 40 subjects6 were randomly selected from a site and randomly assigned to one of two groups (10/group or 20/group). Thickness, surface area, and volume maps from each subject were mapped into the atlas surface space, surface smoothed (2, 4 6, 8, 10, and 12mm FWHM), after which a vertexwise two-group GLM analysis was performed. Clusters were formed by thresholding the vertexwise maps at CFT =.05, .01, .005, and .001. A positive was declared if there were one or more clusters with a clusterwise p-value of less than .05. We do not expect any real group differences since the subjects are young, narrow in age, and group membership is randomly assigned, so any positives are interpreted as false positives. The use of young subjects reduces the chance that age-related changes could produce actual true positives. The analysis was repeated 1000 times, and the number of false positives counted. We would expect 50/1000=5% false positives. A secondary analysis was also performed to determine the maximum nominal cluster p-value for which the actual FPR was 5%. This is useful for evaluating the actual FPR for previously published studies.
p-values for clusters were computed based on smoothed Gaussian Monte Carlo (MCZ) simulations7 (Hagler et al., 2006) and permutation (Hayasaka et al., 2004). In the MCZ method (the default in FreeSurfer), we created look up tables of p-values based on simulations in which a z-field was synthesized on the atlas surface. The z-field was Gaussian smoothed, rescaled to unit standard deviation, and then thresholded; the size of the largest cluster was then extracted. This was repeated 10,000 times for thresholds of p<.05, .01, .005, .001, .0005, and .0001 over a FWHM range of 1–30mm allowing us to compute the probability of a cluster of a given size for a given threshold at a given smoothness level. These tables are distributed in FreeSurfer. When a user analyzes a data set, clusters are extracted from the significance map from the GLM. The p-value for the cluster is determined by indexing into the table based the size of the cluster, the threshold used to form the cluster, and an estimate of the global FWHM (see below). The parametric assumption is that the true data have a Gaussian smoothness describe by the estimated FWHM. Clusters are extracted separately for both hemispheres. The final p-value of a cluster is then corrected for both hemispheres by multiplying the p-value by 2 (i.e., an N=2 Bonferroni correction). This last correction is not applied to the laterality analysis since there is only one surface. Permutation correction was done by permuting the design matrix, recomputing the significance map, thresholding, and extracting the largest cluster over 1000 iterations. The p-value for a cluster in the real data was then computed as the probability of seeing a maximum cluster of that size or larger in a given hemisphere, followed by the correction for two hemispheres (if needed).
The global FWHM of a given analysis is estimated by computing the correlation coefficient between the residuals of nearest neighbors (this is the first lag of a spatial autoregressive series, i.e., the AR1). The residuals are computed from the GLM by subtracting the fitted data from the actual data. The AR1 is averaged over all vertices and then used to compute the estimated FWHM based on an isotropic smooth 2D Gaussian field: , where D is the average inter-vertex distance (Kiebel et al., 1999; Jenkinson, 2000). The FWHM is rounded to the nearest integer for indexing into the cluster probability look up table. To compute the full ACF, the AR calculation is computed at different distances (i.e., second nearest neighbors, third nearest neighbors, etc.).
Simulation Studies: we performed several simulation studies to validate the software as well as to help determine where the false positives were coming from. In the first simulation, we simply replaced the thickness values in native space with spatially white Gaussian noise (WGN-N) after which it was sent through the full pipeline identical with the thickness analysis. Next, we synthesized white Gaussian noise in the atlas space (WGN-A) and sent it through the pipeline. The difference between WGN-A and WGN-N is that WGN-A is not transformed into the atlas space. Third, we replaced the vertex volume/area values in the native space with a map where the value at every vertex was 1.0 (we refer to this as the “JAC” simulation). This was then analyzed as if it were volume or area (i.e., divide by eTIV and perform Jacobian correction). The JAC simulation is designed to isolate the effects of Jacobian correction from individual differences in thickness, area, and volume. Finally, we created simulations of raw MRI images by adding WGN to the MRI volume for a given subject. Twenty such noise instantiations were generated for a single subject. All were then independently analyzed through the full FreeSurfer stream; thickness, area, and volume were extracted and mapped to atlas space; the group of 20 inputs was analyzed in a GLM; finally, the ACF was computed from the residual. This simulation allows us to see how FreeSurfer processing, particularly smoothness constraints on surface placement, affects the ACF.
Longitudinal Analysis: we will argue in the Discussion that elevated FPRs are due to heavy-tailed ACFs which are due to anatomical features unique to individuals. If heavy-tailed ACFs are caused by unique features, then the heavy-tailedness should disappear when the unique features are removed. To evaluate this claim, we analyzed 20 subjects for which we have two measurements for each subject from the MIRIAD data set (Malone et al., 2013; www.ucl.ac.uk/drc/research/methods/miriad-scan-database; 9 female; average age 69.7y). Each subject has two MRIs collected during the same scanning session. These were analyzed separately in FS8 to compute thickness, area, and volume for each time point, which were then mapped into fsaverage space as described above. We then subtracted scan 1 from scan 2 (i.e., a paired difference); this should remove unique anatomical features since the brain will not have changed in the minutes between the two scans. Residuals were computed by subtracting the mean difference over the 20 subjects at each vertex from each of the 20 values. The ACFs were then computed from the paired difference data residuals as well as from each scan separately. The paired difference data is like a longitudinal study where each subject is scanned multiple times to track changes over time. The individual scan data is a cross-sectional study similar to those analyzed above.
Confidence Intervals (CI): 95% CIs appearing in figures were computed assuming a binomial model with frequency of 5% and 1000 trials. As pointed out in Eklund, et al, 2016, this model is not exact for resampling with replacement because the samples are not independent. However, Eklund found that the biggest errors were for a sample size of 40. For most of this study, we use a sample size of 20. For N=20, Eklund, et al, 2016, found that the binomial CIs were very close to the empirically computed CIs.
Results
The WGN-A and WGN-N simulation studies were very close to each other, with average MCZ FPRs being 4.1% and 3.8%, respectively with little or no dependence on applied smoothing level or CFT. Of the 24 FWHM and CFT combinations, WGN-A had 15 FPR measurements within the 95% confidence range with the rest being slightly conservative; WGN-N had 16 FPR measurements within the 95% confidence range with the rest being slightly conservative. The conservativeness is probably due to the MCZ lookup table being generated from a z-map whereas the WGN p-values are computed via a t-map.
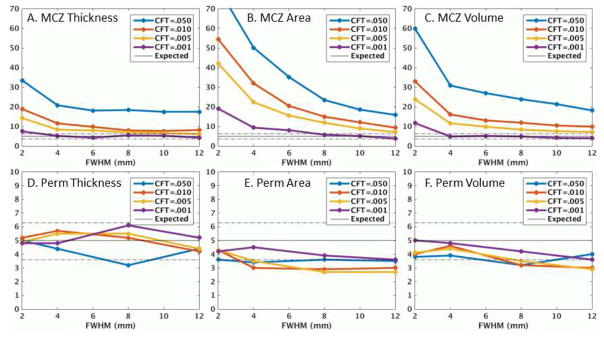
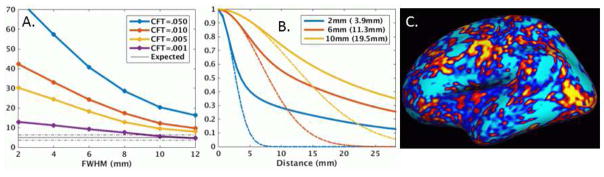
The results for all three sites were very similar (See Figure S1) as were the results across version (Figure S2) and for N=40 (Figure S3), so we report only on the Beijing N=20 sample using version 5.3. Figure 1 shows the FPRs for thickness, surface area, and volume for MCZ and permutation. For MCZ, the FPRs are inflated beyond the expected 5% range, with all showing some smoothing and CFT dependency. Thickness is the best behaved with little dependency on smoothing and threshold (excluding CFT=.05) with many of the FPRs approaching the 95% confidence interval of the nominal FPR. For CFT=.001, almost all data points were within the 95% range. Surface area performs the poorest with strong dependence on smoothing and CFT and FPRs that exceed 20%. The volume measure performs in between thickness and surface area. Figure S4 shows the spatial frequency of false clusters for MCZ FWHM=6mm, CFT=.01. For thickness, the clusters are so sparse, it is hard to say whether they are really concentrated anywhere. Surface area (and JAC) clusters tend to be concentrated in temporal, occipital, and frontal areas. The spatial distribution of false clusters in the volume analysis appears to be fairly random. Returning to Figure 1, the permutation FPRs are almost all within the 95% confidence intervals for the nominal 5% for thickness, area, and volume across all smoothing levels and CFTs.
Figure 1.
Clusterwise false positive rates (%) versus applied smoothing level for thickness, surface area, and volume using either Monte Carlo simulation (MCZ) or permutation (Perm) tests for the Beijing data. Dashed lines are the 95% confidence interval around the ideal 5% value. Note the difference in vertical range between the top and bottom rows.
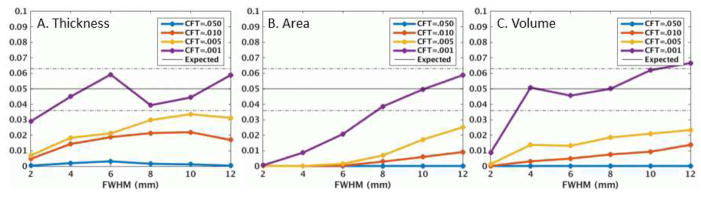
The results in Figure 1 show the actual FPRs when the desired FPR is 5%. However, this figure indicates what is happening for only those clusters near the 5% level. Strong effects, i.e., clusters with MCZ p-values much less than .05, may still have an actual FPR that is less than 5%. To evaluate this, we used the data from Figure 1 to determine the maximum MCZ cluster p-value that would result in the actual FPR being 5%; the results are shown in Figure 2. For a thickness study with CFT<=.01 and FWHM>=6, a cluster would need to have a nominal p-value of .02 or less to be truly significant at the .05 level. For surface area, the nominal p-value would need to be much more significant, and volume somewhere in between. These results are helpful for assessing the true significance of historical data. Numerical values can be found in Tables S1, S2, and S3.
Figure 2.
Maximum nominal MCZ cluster p-value that allows for the actual cluster p-value to be .05 or better. See Tables S1, S2, and S3 in the supplementary data for actual values.
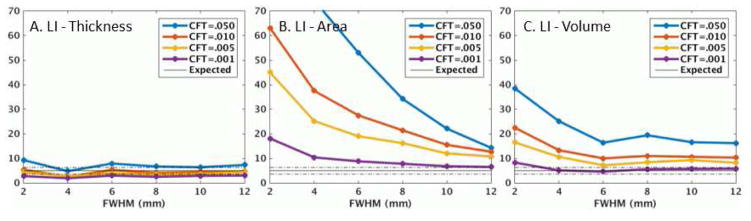
Figure 3 shows the MCZ FPRs for the laterality analysis. In a dramatic departure from the unlateralized analysis, the thickness FPRs are almost all in the 95% confidence interval, even for CFT=.05 and low smoothing levels. In contrast, the laterality analysis has little effect on the surface area FPRs (they actually get slightly worse). The volume FPRs get a little bit better but still very high.
Figure 3.
MCZ clusterwise false positive rate (%) for laterality index (LI) analysis. The values cut off for CFT=.050 in panel B are 96% for FWHM=2mm and 74% for FWHM=4mm. A laterality analysis evaluates asymmetries between the left and right hemispheres.
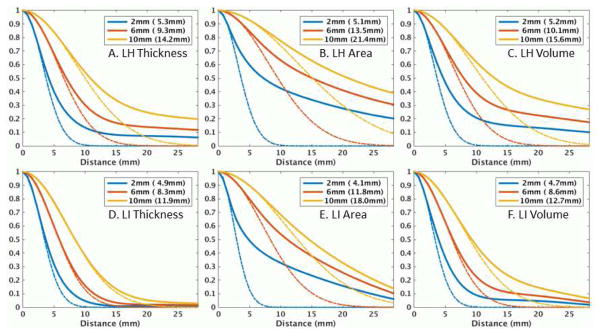
Figure 4 shows the ACFs for the left hemisphere (lh) and the laterality analysis (LI) for set 806 of the Beijing sample for thickness, area, and volume. The dashed line is the ACF for a Gaussian with FWHM based on the AR1 measured from the residuals. The legend has two values; the first value is the applied FWHM, and the value in parentheses is the measured FWHM. The measured FWHM is always greater (sometime much greater) than the applied FWHM indicating the presence of endogenous spatial correlation. All have heavy-tailed (HT) ACFs, with surface area being the worst. The HT ACF is a violation of the Gaussian smoothness assumption in MCZ. As the applied smoothness is increased, the deviation from Gaussianity decreases. In all cases, the overall smoothness and HT drops in the LI analysis. However, for surface area, the reduction in HT is much less than for thickness. This is brought out in Figure S5 which shows a plot of the difference between the expected and actual ACFs for FWHM=6mm. For surface area, the HT reduction does not happen until a distance of 12mm whereas the reduction happens at a much shorter radius for thickness. For this reason, the LI analysis does not affect the MCZ FPRs much for area, whereas it helps considerably for thickness. The LI results suggest that whatever is causing the HT is somewhat symmetric across the hemispheres.
Figure 4.
Residual autocorrelation functions (ACF) for left hemisphere (LH) or laterality index (LI) of Beijing set 806 for nominal smoothing levels of 2, 6, and 10mm. The values in the parentheses are the measured FWHM based on the AR1 value. The dashed lines are the ideal Gaussian ACF based on the measured FWHM. An ACF is heavy-tailed if the actual ACF is greater than the Gaussian ACF. The Distance is the distance along the surface.
Figure 5 shows the residual for a representative subject (sub30556, the 15th subject from the Beijing 806 set) for thickness, surface area, thickness LI, and for WGN smoothed to the FWHM measured from the residuals of the thickness analysis. We show an individual here to demonstrate the unique anatomical features that we will argue in the Discussion are responsible for heavy tails in the ACF. For the unlateralized thickness and area, there are large patches of cortex that have the same sign indicating that those regions deviate from the group mean in the same way (i.e., spatial correlation). These patches represent anatomical properties that are unique to the individual. For the LI thickness analysis, the patches are much smaller. The WGN shows what the patches look like under the ideal case -- the patches are much smaller than the real data, though similar to the LI thickness analysis.
Figure 5.
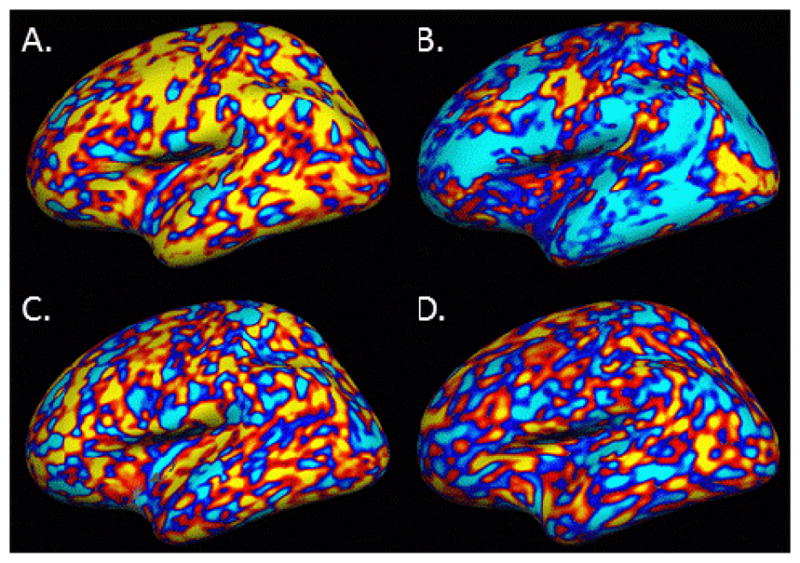
Residual from Subject 15 of Beijing Set 806 (sub30556) displayed on the inflated average surface. A. Thickness, B. Surface Area, C. Thickness laterality index (LI), D. White Gaussian noise smoothed to actual FWHM of Thickness. Red/yellow is a positive difference with the group; blue/cyan is a negative. Patches of same-sign residual indicate anatomical features unique to this subject. A scale bar is not supplied because only the sign of the difference is important for appreciating the patches.
Figure 6 shows the FPRs, the ACF, and residual for the JAC simulation. The FPRs are highly inflated and strongly dependent on smoothing level and CFT. The ACF is also strongly non-Gaussian. The JAC curves are quite similar to those for surface area. There are large patches in the residual similar to those in Figure 5B.
Figure 6.
Results of the JAC simulation. (A) MCZ clusterwise false positive rates. (B) Autocorrelation function (see Figure 4 for explanation). (C) Residual from Subject 15 of Beijing Set 806; note the similarity to Figure 5B.
Figure S6 shows the ACFs for the simulation subject for thickness, area, and volume. The tails are not nearly as heavy for any of the three measurements as compared to when different subjects make up the group, and the overall smoothness is much less. Interestingly, area and volume have about the same smoothness and tail heaviness as thickness.
Figure S7 shows the ACFs for the longitudinal analysis. The two individual time points are very similar to those shown in Figure 4, i.e., heavy tails for all three measurements with area being the worse. The two time points are nearly identical showing good repeatability. However, computing the difference between the two time points caused a substantial drop in smoothness and HT, and the difference between thickness and area or volume becomes much less.
Discussion
This study tested whether parametrically computed clusterwise FPRs are statistically valid in morphological surface-based analysis of cortical thickness, surface area, and volume. Thickness analysis showed slightly inflated FPRs in the range of 5–10% for CFTs<=.01 and FWHM>=4mm, not nearly as bad as for fMRI at matching smoothness and CFT levels. At CFT=.05, the FPR was only 20% (Eklund, et al, did not test at this liberal CFT, but one can assume that the fMRI FPRs would have been much worse). The values are much worse for VBM (Silver et al., 2011) at all CFTs. The thickness FPRs were not strongly dependent on either applied smoothing level or CFT. On the other hand, surface area and volume showed much higher FPRs, in the range of 10–20% at FWHM=6mm and CFT<=.01. This is more in line with the results of Silver et al., 2011 for VBM. Both volume and area FPRs were highly dependent on CFT and applied smoothing. These results were consistent across site, FreeSurfer version, and number of subjects in the group analysis. For thickness interhemispheric (LI) analysis, the MCZ FPRs were almost perfectly controlled, even at CFT=.05. For surface area and volume, the FPRs did not change substantially from the ipsilateral analysis.
As with Eklund et al., 2016, the source of the problem with MCZ was determined to be a HT spatial ACF, which violates the parametric Gaussian assumption. It does not appear that the HT is due to smoothness constraints imposed during surface placement (Figure S6) or some artifact of scanning, since it appears in the results from four different sites. Rather, several pieces of evidence point toward true anatomical features which are unique to each subject as the underlying source of the HT correlation. First, HT is reduced in the cross-hemisphere analysis; this clearly points to an anatomical feature and not an artifact. Second, if HT is caused by unique anatomical features, then HT should be reduced in longitudinal analysis where subtraction of one time point from the next should remove these features; this is indeed what we observe. Visually, these unique features manifest themselves as large same-sign patches in the residual in an individual as shown in Figures 5A, 5B, and 6C.
Surface area and volume both produced much higher FPRs than thickness as well as heavier tailed ACFs. They also produced larger patches in the individual residual (Fig 5A vs 5B and 6C). The JAC simulation shows that even when area or volume vertices are set to 1.0 for all vertices and subjects, the FPRs are inflated and dependent on smoothing level and CFT. The JAC ACF is also strongly non-Gaussian, and there are very large subject-specific patches in the residual (Figure 6C) just as in the volume and area analyses. These are likely caused by the Jacobian correction, which is needed to conserve the total quantity (area or volume) in the presence of stretching and compression in the nonlinear intersubject registration. It is not surprising that large patches of the Jacobian would have the same sign for a subject since an entire gyrus or sulcus needs to be stretched or compressed to fit the atlas. Nor is it surprising that the Jacobian patches would be unique to a subject since they represent the registration of that subject to the atlas. The HT in area and volume is reduced somewhat in the cross-hemisphere analysis and reduced substantially in the longitudinal analysis. In the simulation of the individual subject, the ACFs for area and volume are very similar to thickness. These all point in the direction of the Jacobian correction being a unique anatomical feature that exacerbates the HT in the ACF beyond that seen in thickness alone but that can be reduced through subtraction from the contralateral hemisphere or another time point.
This Jacobian effect will likely be present in any analysis that has Jacobian correction, such as voxel-based morphometry (VBM, Ashburner et al., 2000)). Indeed, Silver et al., 2011 found highly elevated FPRs in VBM when using RFT cluster correction and Scarpazza et al., 2013, found inflated FPRs when using clusterwise RFT correction in a single subject, though neither examined the ACF.
While thickness does not require a Jacobian correction, the stretching and compression are still taken into account through local averaging or replication which could theoretically have an effect on the FPRs. This does not appear to have a significant effect as the WGN-N experiment (where the averaging/replication is present) had near identical FPRs to those of the WGN-A experiment (where the averaging/replication is not present). The FPR differences between thickness and area/volume/VBM caused by Jacobian correction have implications for statistical power and choice of anatomical measure. Consider the case where thickness and volume studies have the same power curve (i.e., the true positive rate (TPR) vs. FPR) where positives are declared when the RFT/MC cluster p-value less than .05 with CFT=.01. Under these conditions, both studies would be operating at an actual FPR of greater than 5%, but the actual FPR of the volume study would be much greater than that of the thickness study. This would push the volume study further out on the power curve and give it an apparently higher TPR than the thickness study even though, by construction, they are the same. This could make thickness studies appear to have less power than volume studies (or any study where the underlying measure requires a Jacobian correction). In these cases, permutation must be used to assure that the two methods are operating at the same FPR. It is impossible to say from this data whether the actual power curves are different between thickness and area/volume/VBM; the question may not make sense given that they are all measuring different features. However, we can say that any measure requiring Jacobian correction will have to have a much larger cluster size than thickness because large clusters are so much more frequent under the null.
The implications for previously published studies that use MCZ are mixed. The majority of the surface-based morphometry studies are thickness-based, and many of those use CFT<=.01 and FWHM>5mm (FreeSurfer does not have default CFT or FWHM values). In those cases, the FPRs will only be slightly inflated. Further, the results in Figure 1A only apply to clusters that were significant at the p=.05 level. Larger, more significant clusters (“strong effects”) might still be significant at the .05 level as indicated in Figure 2. Thickness lateralization/asymmetry studies would need no caveats. For surface area studies, the repercussions are much more worrisome as one really needs to use CFT=.001 and smooth by 8–10mm to achieve a nominal FPR, and effects would have to be very strong to stay significant. For volume analysis, one also needs CFT=.001 for weak effects, but for strong effects, a cluster would need p=.005 at CFT<=.01 and FWHM>=6mm to stay significant at the 5% level. We did not test MCZ FPRs in longitudinal analysis, but the improved Gaussianity we observed should result in fairly well controlled MCZ FPRs.
For future studies, there are several options. For thickness or volume studies, one could use MCZ with CFT<=.001 with any smoothness level or CFT<=.005 with FWHM>10mm. For surface area, one would need CFT<=.001 and FWHM>10mm. The problem with such stringent CFTs is that there are often no voxels that survive; this is a huge disadvantage as it will greatly reduce the TPR/power. Permutation is attractive because it makes fewer assumptions about the data than parametric methods, and, perhaps more importantly, it allows for less stringent CFTs. Permutation has some disadvantages, however. The correction is computationally intensive, though it is possible to reduce the computation time by fitting the tails to an analytic formula (Winkler et al., 2016). Permutation requires that the data be exchangeable across subject. Exchangeability is a complicated topic in permutation but generally requires that the joint distribution of the noise across measurements not change under permutation. This can be violated in very simple and common circumstances like the presence of a nuisance age effect (i.e., non-orthogonal design matrices). This is potentially a significant drawback because the vast majority of studies have such nuisance variables. However, there are approximations that seem to work well (Winkler et al., 2014). Exchangeability may be violated when two groups have different variances, though this can be overcome through sign flipping (Winkler et al., 2014). Permutation is less powerful than its parametric counterpart when the parametric assumptions are met (Nichols et al., 2001), though the loss of power may be small (Winkler et al., 2014). Permutation is more complicated to set up, especially for complicated designs like mixed effects models; this will be an added burden to the neuroimager who is not statistically savvy. Software to perform surface-based permutation analysis does exist. The FreeSurfer mri_glmfit-sim script can be run with the –perm option; the currently released version can only be applied to orthogonal designs, but we have recently created a software patch to handle non-orthogonal designs using the ter Braak approximation tested in Winkler et al., 2014. Winkler et al., 2014, recommend the Freeman-Lane method over ter Braak, but ter Braak performed similarly on power but was only a little more liberal. We implemented the ter Braak method because it fit easily within our current framework, making a simple software patch possible; we will implement Freeman-Lane for release in future FreeSurfer versions. Permutation Analysis of Linear Models (PALM, fsl.fmrib.ox.ac.uk/fsl/fslwiki/PALM) provides extensive permutation functionality and can be run in a surface-based mode. Another parametric solution is to measure the ACF in a data set and then perform the Monte Carlo analysis by smoothing WGN using the empirical ACF, as is now offered by AFNI (afni.nimh.nih.gov, Cox et al., 2017) for volume-based analysis. However, while this is fast for volume-based analysis that can use the FFT, it will be very slow for surface-based analysis because the iterative nearest neighbor smoothing operation is slow. It would not be possible to distribute pre-computed tables as we do now, so a user would have to run the simulation on a case-by-case basis. In this case, the time is probably better spent doing permutation.
The analysis we have presented makes the assumption that the surface maps have uniform smoothness as measured by the FWHM. Non-stationarity affects RFT and MC as well as permutation. In RFT and MC, a global estimate of the FWHM is computed and used to perform the correction. Non-stationarity will cause clusters in areas of higher-than-average smoothness to have too small a p-value, increasing false positives in these areas, while causing areas of lower-than-normal smoothness to be too conservative. To overcome this in RFT, Worsley et al., 1999 used a voxel-specific measure of the FWHM to adjust the size of the cluster, though this method will still be sensitive to the non-Gaussian smoothness discussed here. A stationary permutation test properly controls the FPR under non-stationary conditions but loses sensitivity less-smooth areas. Hayasaka et al., 2004 and Salimi-Khorshidi et al., 2011 implemented a permutation method in which the cluster size used to compute the null distribution was adjusted by the local FWHM. Spatial non-stationarity has been observed in both fMRI (Hayasaka et al., 2004) and VBM (Ashburner et al., 2000). Non-stationarity has not been fully evaluated for surface-based operations. However, the MCZ false cluster frequency maps (Figure S4) indicate the false clusters are not uniformly distributed across cortex; this non-uniformity is evidence of non-stationarity. It is our intention to incorporate non-stationarity into the FreeSurfer permutation test.
Conclusions
False positives are an inevitable part of science and should not be seen as catastrophic. Nevertheless, software developers and researchers need to take steps to understand and adequately control for false positives. In this study, inflated parametric FPRs were found for surface-based morphological analysis of cortical thickness, surface area, and volume. For thickness, the FPRs were in the range of 10% instead of the desired 5% for typical analysis parameters, much less than has been found for fMRI or VBM analysis at matching cluster forming thresholds. For surface area and volume, the FPRs were much higher, at times rivaling that of fMRI and VBM. The inflated FPRs were driven by non-Gaussian, heavy-tailed ACFs resulting from large patches where a subject’s unique anatomy differed from that of the group; these were made worse by the Jacobian correction implicitly used for area and volume analysis. Fortunately, most surface-based studies using FreeSurfer use thickness. In inter-hemispheric analysis, where one compares a vertex value to its homologous vertex on the opposite hemisphere, we found good parametric control of FPRs for thickness but not for surface area or volume. It is likely that longitudinal studies will have good control of MCZ FPRs, although this was not explicitly tested. As with fMRI and VBM, the FPRs were brought into line by using high thresholds and smoothing levels or by using non-parametric permutation instead of Gaussian-based MCZ. The presence of inflated FPRs does not necessarily invalidate previous studies because many have strong effects that would have been significant even after adequate control of FPRs.
Supplementary Material
Acknowledgments
Support for this research was provided in part by the National Institutes of Biomedical Imaging and Bioengineering (1R01EB023281, 1R21EB018964-01, P41EB015896, R01EB006758, R21EB018907, R01EB019956), the National Institute on Aging (5R01AG008122, R01AG016495), the National Institute of Diabetes and Digestive and Kidney Diseases (1-R21-DK-108277-01), the National Institute for Neurological Disorders and Stroke (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625), and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by the NIH Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project. We would like to thank the contributors to and curators of the 1000 Functional Connectomes data set. Some of data used in the preparation of this article were obtained from the MIRIAD database. The MIRIAD investigators did not participate in analysis or writing of this report. The MIRIAD dataset is made available through the support of the UK Alzheimer’s Society (Grant RF116). The original MIRIAD data collection was funded through an unrestricted educational grant from GlaxoSmithKline (Grant 6GKC). We would also like to thank Lee Terrill and Dr. Martin Reuter for their assistance on the MIRIAD data set.
Footnotes
The authors are two of the primary developers of FreeSurfer.
The RFT-based SurfStat package (www.math.mcgill.ca/keith/surfstat; Chung et al., 2010) has also been used.
We emphasize here that volume is computed from the surface and should not be confused with VBM.
FreeSurfer 6.0 computes volume using a truncated trilateral pyramid (Winkler et al., 2017).
By “curvature” we mean the spatially smoothed mean curvature, which is the average of the two principal curvatures.
For the N=40 analysis, only the left hemisphere thickness in the Beijing group was analyzed.
Eklund, et al, 2016, found a small bug in the AFNI MC simulator (alphasim). This bug is not present in the FreeSurfer MC simulation program and ended up having a minor effect on the AFNI FPRs (Cox et al., 2017).
We did not use the specialized FreeSurfer longitudinal pipeline to maintain consistency with the other analyses in this manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ashburner J, Friston KJ. Voxel-based morphometry--the methods. Neuroimage. 2000;11(6 Pt 1):805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Benjamin DJ, Berger JO, Johnson VE. Commentary: Redefine statistical significance. Nature Human Behaviour. 2017 doi: 10.1038/s41562-017-0189-z. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Head D, Parker J, Fotenos AF, Marcus D, Morris JC, Snyder AZ. A unified approach for morphometric and functional data analysis in young, old, and demented adults using automated atlas-based head size normalization: reliability and validation against manual measurement of total intracranial volume. Neuroimage. 2004;23(2):724–738. doi: 10.1016/j.neuroimage.2004.06.018. [DOI] [PubMed] [Google Scholar]
- Carp J. The secret lives of experiments: methods reporting in the fMRI literature. Neuroimage. 2012;63(1):289–300. doi: 10.1016/j.neuroimage.2012.07.004. [DOI] [PubMed] [Google Scholar]
- Chung MK, Worsley KJ, Nacewicz BM, Dalton KM, Davidson RJ. General multivariate linear modeling of surface shapes using SurfStat. Neuroimage. 2010;53(2):491–505. doi: 10.1016/j.neuroimage.2010.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW, Chen G, Glen DR, Reynolds RC, Taylor PA. FMRI Clustering in AFNI: False-Positive Rates Redux. Brain Connect. 2017;7(3):152–171. doi: 10.1089/brain.2016.0475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Eklund A, Nichols TE, Knutsson H. Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proc Natl Acad Sci U S A. 2016;113(28):7900–7905. doi: 10.1073/pnas.1602413113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences. 2000;97:11044–11049. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo BT, … Zilles K. Cortical folding patterns and predicting cytoarchitecture. Cereb Cortex. 2008;18(8):1973–1980. doi: 10.1093/cercor/bhm225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Albert M, Dieterich M, Haselgrove C, Kouwe Avd, … Dale AM. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999a;9(2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RBH, Dale AM. High-resolution inter-subject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1999b;8(4):272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flandin G, Friston K. Analysis of family-wise error rates in statistical parametric mapping using random field theory. 2016 doi: 10.1002/hbm.23839. https://arxiv.org/abs/1606.08199. [DOI] [PMC free article] [PubMed]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magn Reson Med. 1995;33(5):636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Worsley KJ, Frackowiak RS, Mazziotta JC, Evans AC. Assessing the significance of focal activations using their spatial extent. Hum Brain Mapp. 1994;1(3):210–220. doi: 10.1002/hbm.460010306. [DOI] [PubMed] [Google Scholar]
- Greve DN, Van der Haegen L, Cai Q, Stufflebeam S, Sabuncu MR, Fischl B, Brysbaert M. A surface-based analysis of language lateralization and cortical asymmetry. J Cogn Neurosci. 2013;25(9):1477–1492. doi: 10.1162/jocn_a_00405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagler DJ, Jr, Saygin AP, Sereno MI. Smoothing and cluster thresholding for cortical surface-based group analysis of fMRI data. Neuroimage. 2006;33(4):1093–1103. doi: 10.1016/j.neuroimage.2006.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayasaka S, Nichols TE. Validating cluster size inference: random field and permutation methods. Neuroimage. 2003;20(4):2343–2356. doi: 10.1016/j.neuroimage.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Hayasaka S, Phan KL, Liberzon I, Worsley KJ, Nichols TE. Nonstationary cluster-size inference with random field and permutation methods. Neuroimage. 2004;22(2):676–687. doi: 10.1016/j.neuroimage.2004.01.041. [DOI] [PubMed] [Google Scholar]
- Jenkinson M. Technical Report TR00MJ3: Estimation of Smoothness from the Residual Field. 2000 https://www.fmrib.ox.ac.uk/datasets/techrep/tr00mj3/tr00mj3.pdf.
- Keller SS, Roberts N, Garcia-Finana M, Mohammadi S, Ringelstein EB, Knecht S, Deppe M. Can the language-dominant hemisphere be predicted by brain anatomy? J Cogn Neurosci. 2011;23(8):2013–2029. doi: 10.1162/jocn.2010.21563. [DOI] [PubMed] [Google Scholar]
- Kiebel SJ, Poline JB, Friston KJ, Holmes AP, Worsley KJ. Robust smoothness estimation in statistical parametric maps using standardized residuals from the general linear model. Neuroimage. 1999;10(6):756–766. doi: 10.1006/nimg.1999.0508. [DOI] [PubMed] [Google Scholar]
- Klein A, Ghosh SS, Avants B, Yeo BT, Fischl B, Ardekani B, … Parsey RV. Evaluation of volume-based and surface-based brain image registration methods. Neuroimage. 2010;51(1):214–220. doi: 10.1016/j.neuroimage.2010.01.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Bodurka J, Bendettini P. Artifactual Time-Course Correlations in Echo-Planar fMRI with Implications for Studies of Brain Function. International Journal of Imaging Systems and Technology. 2008;18:345–349. [Google Scholar]
- Malone IB, Cash D, Ridgway GR, MacManus DG, Ourselin S, Fox NC, Schott JM. MIRIAD--Public release of a multiple time point Alzheimer’s MR imaging dataset. Neuroimage. 2013;70:33–36. doi: 10.1016/j.neuroimage.2012.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Lindenberg A, Nicodemus KK, Egan MF, Callicott JH, Mattay V, Weinberger DR. False positives in imaging genetics. Neuroimage. 2008;40(2):655–661. doi: 10.1016/j.neuroimage.2007.11.058. [DOI] [PubMed] [Google Scholar]
- Mueller K, Lepsien J, Möller HE, Lohmann G. Commentary: Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rate. Frontiers in Human Neuroscience. 2017;11:345. doi: 10.3389/fnhum.2017.00345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric Permutation Tests for functional Neuroimaging: A Primer with Examples. Human Brain Mapping. 2001;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Smith SM, Nichols TE. Adjusting the effect of nonstationarity in cluster-based and TFCE inference. Neuroimage. 2011;54(3):2006–2019. doi: 10.1016/j.neuroimage.2010.09.088. [DOI] [PubMed] [Google Scholar]
- Salmond CH, Ashburner J, Vargha-Khadem F, Connelly A, Gadian DG, Friston KJ. Distributional assumptions in voxel-based morphometry. Neuroimage. 2002;17(2):1027–1030. [PubMed] [Google Scholar]
- Scarpazza C, Nichols TE, Seramondi D, Maumet C, Sartori G, Mechelli A. When the Single Matters more than the Group (II): Addressing the Problem of High False Positive Rates in Single Case Voxel Based Morphometry Using Non-parametric Statistics. Front Neurosci. 2016;10:6. doi: 10.3389/fnins.2016.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarpazza C, Sartori G, De Simone MS, Mechelli A. When the single matters more than the group: very high false positive rates in single case Voxel Based Morphometry. Neuroimage. 2013;70:175–188. doi: 10.1016/j.neuroimage.2012.12.045. [DOI] [PubMed] [Google Scholar]
- Scarpazza C, Tognin S, Frisciata S, Sartori G, Mechelli A. False positive rates in Voxel-based Morphometry studies of the human brain: should we be worried? Neurosci Biobehav Rev. 2015;52:49–55. doi: 10.1016/j.neubiorev.2015.02.008. [DOI] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22(3):1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Silver M, Montana G, Nichols TE Alzheimer’s Disease Neuroimaging I. False positives in neuroimaging genetics using voxel-based morphometry data. Neuroimage. 2011;54(2):992–1000. doi: 10.1016/j.neuroimage.2010.08.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler AM, Greve DN, Bjuland KJ, Nichols TE, Sabuncu MR, Haberg AK, … Rimol LM. Joint analysis of cortical area and thickness as a replacement for the analysis of the volume of the cerebral cortex. Cereb Cortex. 2017 doi: 10.1093/cercor/bhx308. Accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler AM, Ridgway GR, Douaud G, Nichols TE, Smith SM. Faster permutation inference in brain imaging. Neuroimage. 2016;141:502–516. doi: 10.1016/j.neuroimage.2016.05.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014;92:381–397. doi: 10.1016/j.neuroimage.2014.01.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler AM, Sabuncu MR, Yeo BT, Fischl B, Greve DN, Kochunov P, … Glahn DC. Measuring and comparing brain cortical surface area and other areal quantities. Neuroimage. 2012;61(4):1428–1443. doi: 10.1016/j.neuroimage.2012.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo CW, Krishnan A, Wager TD. Cluster-extent based thresholding in fMRI analyses: pitfalls and recommendations. Neuroimage. 2014;91:412–419. doi: 10.1016/j.neuroimage.2013.12.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley KJ, Andermann M, Koulis T, MacDonald D, Evans AC. Detecting changes in nonisotropic images. Hum Brain Mapp. 1999;8(2–3):98–101. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<98::AID-HBM5>3.0.CO;2-F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley KJ, Evans AC, Marrett S, Neelin P. A Three Dimensional Statistical Analysis for CBF Activation Studies in Human Brain. Journal of Cerebral Blood Flow and Metabolism. 1992;12:900–918. doi: 10.1038/jcbfm.1992.127. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.