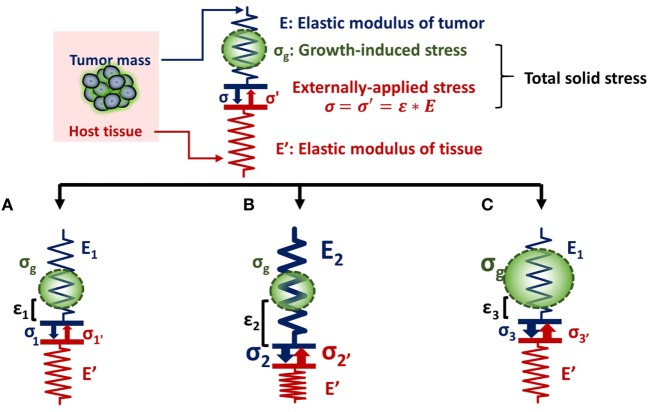
Figure 1.

Solid stress and stiffness are two distinct biomechanical abnormalities present in the tumor microenvironment. (A) According to the simple analogy of a spring that obeys Hooke’s law σ = E ⋅ ε, when a tumor grows and pushes the surrounding host tissue of elastic modulus E’, it results in a deformation ε₁ and a stress, σ₁. As a consequence, the host tissue returns an equal and opposite stress σ₁′, which is defined as externally applied solid stress (σ₁ = σ₁′). This externally applied stress, in combination with the growth-induced stress (σ_g), generated from mechanical interactions within the tumor, constitutes the total solid stress transmitted in the tumor interior. (B) In the case that the tumor stiffens so that E₂ is greater than E₁ (E₂ > E₁), the tumor can increase in size and the deformation ε₂ is greater than ε₁ (ε₂ > ε₁). The externally applied stress (σ₂′) and finally the total solid stress accumulated in the tumor interior are greater than that in (A) without any change in the growth-induced stress. (C) The growth-induced solid stress, however, increases during growth, while tumor stiffening might remain the same (16). In this case, the externally applied solid stress σ₃′ can be equal to σ₁′, but total solid stress increases. Therefore, the resultant stress transmitted in the tumor interior is greater than that in (A) without any change in tumor stiffness.