BEESEM: estimation of binding energy models using HT-SELEX data

Abstract

Motivation

Characterizing the binding specificities of transcription factors (TFs) is crucial to the study of gene expression regulation. Recently developed high-throughput experimental methods, including protein binding microarrays (PBM) and high-throughput SELEX (HT-SELEX), have enabled rapid measurements of the specificities for hundreds of TFs. However, few studies have developed efficient algorithms for estimating binding motifs based on HT-SELEX data. Also the simple method of constructing a position weight matrix (PWM) by comparing the frequency of the preferred sequence with single-nucleotide variants has the risk of generating motifs with higher information content than the true binding specificity.

Results

We developed an algorithm called BEESEM that builds on a comprehensive biophysical model of protein–DNA interactions, which is trained using the expectation maximization method. BEESEM is capable of selecting the optimal motif length and calculating the confidence intervals of estimated parameters. By comparing BEESEM with the published motifs estimated using the same HT-SELEX data, we demonstrate that BEESEM provides significant improvements. We also evaluate several motif discovery algorithms on independent PBM and ChIP-seq data. BEESEM provides significantly better fits to in vitro data, but its performance is similar to some other methods on in vivo data under the criterion of the area under the receiver operating characteristic curve (AUROC). This highlights the limitations of the purely rank-based AUROC criterion. Using quantitative binding data to assess models, however, demonstrates that BEESEM improves on prior models.

Availability and Implementation

Freely available on the web at http://stormo.wustl.edu/resources.html.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Sequence-specific, DNA-binding transcription factors (TFs) control the expression of genes in all organisms. In most species they constitute between 5% and 10% of all genes (de Boer and Hughes, 2012; Rhee et al., 2014; Vaquerizas et al., 2009). Variations in either the TFs or their binding sites are associated with changes in gene expression, often with deleterious phenotypes, but are also associated with evolutionary divergence between species (Carroll, 2005; Zheng et al., 2011). Despite the importance of these TFs, the sequence specificity is known for only a small fraction of them. Even in most well-studied species, the majority of TFs have unknown specificity (Weirauch et al., 2014).

Several high-throughput experimental methods have been developed for determining the specificity of TFs (reviewed in Stormo and Zhao, 2010). Some methods measure the fluorescence from TFs over thousands of DNA probes that contain millions of different possible DNA binding sites. Others take advantage of high-throughput sequencing technologies to determine selective enrichments of binding sites from millions of short sequence reads. Regardless of the technology used, computational analysis of the data is required to extract the desired specificity information for the TF and different programs vary widely in their ability to make accurate predictions of binding sites over a wide range of affinities (Weirauch et al., 2013).

Protein binding microarrays (PBMs), and related methods (Berger et al., 2006; Nutiu et al., 2011; Puckett et al., 2007), utilize arrays of double-stranded DNA to which TF binding can be assayed with fluorescent antibodies to the proteins. Several large-scale PBM experiments have been published in which the specificities of several hundred (Badis et al., 2008, 2009; Berger et al., 2008; Gordan et al., 2011; Najafabadi et al., 2015; Narasimhan et al., 2015), and even over 1000 (Weirauch et al., 2014), TFs have been determined. It was shown that the quality of the motif, the fit to the data and the ability to predict TF binding in an independent experiment varied considerably depending on the algorithm used (Zhao and Stormo, 2011). In a detailed comparison of 26 different algorithms for analyzing PBM data a wide range of accuracies were found (Weirauch et al., 2013). For the vast majority of TFs (∼90%), simple position weight matrices (PWMs), additive models with scores assigned to each base at each position, fit the data as well as more complex models when the best algorithms were used. The best methods employed a biophysical model of protein–DNA interactions (Djordjevic et al., 2003; Foat et al., 2006; Zhao et al., 2009). Recent enhancements to the FeatureREDUCE algorithm provide further improvements to the accuracy of motif inference from PBM data (Riley et al., 2015). The BindSter algorithm (Locke and Morozov, 2015) also provides improved motif inference for both PBM and MITOMI (Rockel et al., 2012) data.

SELEX (Tuerk and Gold, 1990) has also been adapted to utilize high-throughput sequencing (Jolma et al., 2010; Ogawa and Biggin, 2012; Riley et al., 2014; Slattery et al., 2011; Wong et al., 2011; Zykovich et al., 2009; Zhao et al., 2009), most commonly called high-throughput SELEX (HT-SELEX) or alternatively SELEX-seq. After one or more rounds of selection, the bound fraction, as well as the input DNA, are sequenced to high depth. Those sequences are used to infer a model of specificity, typically a PWM, for the TF. Some methods using biophysical models have been developed for the HT-SELEX problem (Atherton et al., 2012; Orenstein and Shamir, 2015; Riley et al., 2014) but only HTS-IBIS has been widely tested. In addition, the recent DeepBind algorithm (Alipanahi et al., 2015), which is based on deep convolutional neural networks, reports improved predictions of in vivo data, even when it is trained on in vitro HT-SELEX data. The most commonly used method for inferring motifs from HT-SELEX data uses the most highly selected sites from later rounds and builds a PWM by comparing the frequency of the preferred site with single-nucleotide variants (Jolma et al., 2010, 2013; Nitta et al., 2015). This approach does not take advantage of the entire range of binding affinities and has the risk of producing ‘over-specified’ motifs, with higher information content than the true binding specificity. In a comparison of methods for the zinc finger protein Bcl6 we found that motifs inferred from PBM and bacterial one-hybrid data were very similar to each other and also to a motif inferred using MEME on ChIP-seq data (Gupta et al., 2014). The HT-SELEX motif for Bcl6 had much higher information content and was less effective in identifying binding sites in the ChIP-seq dataset (at equivalent P-value cutoffs), suggesting the over-specification phenomenon. In another comparison between PBM and HT-SELEX motifs for the same TFs, Orenstein and Shamir (2014) also found that the PBM motifs fit the quantitative binding data better, but they found that the HT-SELEX motifs performed better on ChIP-seq data, using the criterion of the area under the receiver operating characteristic curve (AUROC).

We introduced the BEEML (Binding Energy Estimates using Maximum Likelihood) method that finds the best fit to the data over the parameters of the PWM and the TF concentration (Zhao et al., 2009). The biophysical model underlying BEEML is suitable for the analysis of HT-SELEX data, but BEEML assumes the location of the binding site on each sequence is known (only the orientation has to be inferred). In a general HT-SELEX experiment, however, the randomized region is much longer than the binding site; typical randomized regions are 20 bp or more while most binding motifs are 10 bp or less. Thus BEEML is limited to HT-SELEX experiments with short randomized regions.

This paper has two main purposes. First, we introduce BEESEM (short for Binding Energy Estimation on SELEX with Expectation Maximization), which extends BEEML to work on HT-SELEX data with long randomized regions. We extend the biophysical model used in BEEML to the case with long sequences containing shorter binding sites so that the sites must be inferred in addition to the motif. We do this using an expectation maximization (EM) approach similar to a previously introduced method for motif discovery on unaligned co-regulated gene sets (Lawrence and Reilly, 1990), but including nonlinear regression to fit the quantitative enrichment data as part of the maximization step. The method also allows us to calculate confidence intervals on the estimated parameters. Second, we assess BEESEM against other modeling approaches using HT-SELEX data, as well as PBM and ChIP-seq data from independent experiments. The results demonstrate that the BEESEM motifs achieve significantly better fits to the quantitative HT-SELEX data and we also show that they perform much better than other HT-SELEX binding models on PBM data and equally well or better on ChIP-seq data.

2 Materials and methods

2.1 Materials

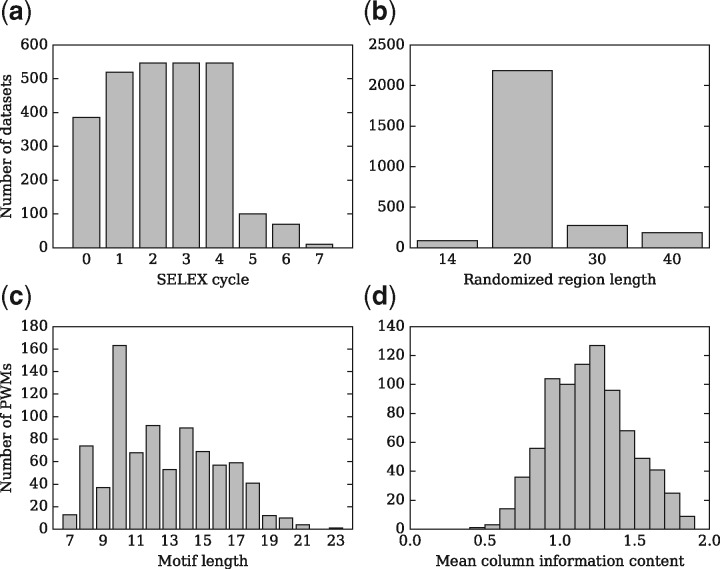
A total of 2726 HT-SELEX sequencing datasets generated by Jolma et al. (2013) were retrieved from the European Nucleotide Archive (www.ebi.ac.uk/ena). These datasets were grouped into 547 HT-SELEX experiments, each of which is composed of 4 to 7 SELEX cycles (Fig. 1a). A total of 463 distinct TFs were surveyed in these experiments. In a typical experiment, the TF of interest binds to DNA probes that consist of a randomized region and two constant flanking regions. The length of the randomized region varies between experiments (Fig. 1b). We focus on the experiments in which the randomized region is 20 bp because they form the largest group. A total of 843 PWMs were also published in Jolma et al. (2013), which we refer to as the J2013 PWMs. To assess their specificity, we calculated the mean column information content (MCIC), which is defined as the average information content of all the columns in a matrix. Figure 1d shows that the average MCIC of the J2013 PWMs is 1.20 bit.

Fig. 1.

The HT-SELEX experiments and the J2013 PWMs. (a) Most of the HT-SELEX experiments have 4 cycles. By convention, the 0th SELEX cycle denotes the initial library of randomly generated DNA probes. Multiple HT-SELEX experiments share the same initial library. 27 sequencing datasets corresponding to the 1st cycle are missing from the database. (b) In 80% of the datasets, the randomized region is 20 bp long. (c) The length of the J2013 PWMs ranges from 7 to 23; the mean length is 12.7 bp. (d) The average mean column information content of the J2013 PWMs is 1.20 bit. The information content is computed based on a uniform background distribution of the four nucleotides

2.2 Biophysical model

The biophysical model underlying BEESEM characterizes the interaction between a TF and DNA sequences of different affinities. It generalizes the BEEML model (Zhao et al., 2009) and allows simultaneous estimation of the binding motif and the locations of binding sites. The BEEML model states that the probability of finding a sequence S_i among all the DNA molecules bound by the TF is

$$P(S_i|B)=\frac{P(S_i)}{P(B)}\frac{e^{-E_i}}{e^{-E_i}+e^{-\mu }}.$$ (1)

$P(S_i)$ is the proportion of sequence S_i before TF binding and P(B) is the overall probability of a DNA molecule being bound by the TF. In addition, B represents the collection of bound DNA molecules, E_i is the binding energy of sequence S_i and μ is the chemical potential of the TF. Equation (1) assumes that the DNA sequence length l is the same as the motif length m. However, l is generally larger than m and the binding site may be located anywhere on the sequence. As a result, each protein–DNA complex has $2(l-m+1)$ possible configurations, if we account for both orientations. To keep track of the different complexes and their configurations, we use $T·S_i^k$ to denote the kth configuration of the protein–DNA complex of S_i, where T represents the TF, $k=1,2,\dots ,2(l-m+1)$. Under this notation, $S_i^k$ can also be interpreted as the binding sequence in $T·S_i^k$ and is therefore associated with a binding energy (denoted by $E(S_i^k)$). $E(S_i^k)$ is entirely determined by the DNA sequence of $S_i^k$, regardless of its location on sequence S_i. Specifically, we assume the binding energy can be represented by the inner product of an energy PWM (Stormo, 2013) and the encoding vector of a DNA sequence. Thus $E(S_i^k)$ can also be written as $E(s_j)$, if $S_i^k=s_j$, where s_j represents the DNA sequence of a specific m-mer. To generalize Equation (1), we rearrange it and replace the symbol S_i with s_j, namely

$$\frac{P(s_j|B)}{\tilde{P}(s_j)}=\frac{1}{P(B)}\frac{e^{-E(s_j)}}{e^{-E(s_j)}+e^{-\mu }}.$$ (2)

$\tilde{P}(s_j)$ represents the effective proportion of s_j prior to TF binding, where ‘effective’ means the sequence count of s_j is discounted because we assume that two or more proteins cannot bind to the same sequence at the same time. For example, let us consider the scenario that the same m-mer s₁ occurs twice on a DNA sequence. Since at most one of them can be bound by the TF due to physical hindrance, the effective count of s₁ on this DNA sequence is only one. To simplify the LHS of Equation (2), we use R_j to denote the ratio $P(s_j|B)/\tilde{P}(s_j)$. In the following section, we will show how to use the EM algorithm to compute R_j from data. By fitting Equation (2) to the computed R_j, we can estimate the unknown parameters in our model (collectively represented by a vector $\mathit{\theta }$), which include the PWM (which contains the energy of each base relative to the preferred base in units of kT), the chemical potential and some auxiliary parameters (see Supplementary information for a detailed description of the model and its parameters).

2.3 Algorithm

2.3.1 Parameter estimation

BEESEM uses the EM algorithm to iteratively find both the optimal PWM and the most likely binding position on each sequence read. The EM algorithm consists of multiple rounds and each round has two steps: an expectation step (E step) and a maximization step (M step). In the E step, we use the current estimate of the PWM (or an initial guess) to calculate the probability distribution of binding sites on each sequence. Specifically, we assume the probability of an m-mer subsequence being the binding site is proportional to its affinity score predicted by the current PWM. Also we require that the probabilities of all the m-mers on sequence S_i sum to $P(1|S_i)$. $P(1|S_i)$ represents the probability that S_i is bound by the TF and therefore contains a binding site, and it can be computed using the Bayes’ theorem:

$$P(1|S_i)=\frac{P(S_i|1)P(1)}{P(S_i|1)P(1)+P(S_i|0)P(0)}.$$ (3)

In the above equation, $P(S_i|1)$ is the proportion of S_i among bound sequence reads, $P(S_i|0)$ is the proportion of S_i among unbound sequence reads, P(1) is the ex ante probability that a sequence read is bound by the TF, and P(0) is the probability of the complementary event, thus $P(0)=1-P(1)$. P(1) can be approximated by the mean of the $P(1|S_i)$ values from the previous round. After computing the probability distribution of binding sites on each sequence, we can easily calculate the probability $P(s_j|B)$ in Equation (2) and finally the ratio R_j. In the M step, we search for a parameter vector $\mathit{\theta }$ that maximizes the probability of observing the R_j values computed in the E step. R_j is a ratio of two positive numbers, so it likely follows a log-normal distribution. However, for convenience, we assume it can be approximated by a normal distribution in the regime of the data, and define the maximum likelihood estimate of $\mathit{\theta }$ by fitting Equation (2) with least squares minimization. In other words, the objective function of the nth round is

(4)

where $R_j^{(n)}$ denotes the computed R_j value in the nth round and $R_j(\mathit{\theta })$ represents the RHS of Equation (2). The Supplementary information contains a proof that Equation (4) is the correct objective function and therefore the procedure described above is indeed an EM algorithm. The minimization is performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Zhu et al., 1997), which is a quasi-Newton hill-climbing method for solving nonlinear optimization problems. A major challenge for any hill-climbing method is that the search for a global minimum of the objective function may be attracted to a local minimum. Thus it is important to select a proper starting point (denoted by ${\mathit{\theta }}_0$), since it largely determines the endpoint of a search. Conventionally ${\mathit{\theta }}_0$ is randomly generated and multiple searches are attempted. However, our preliminary results (unpublished data) indicate that θ may change significantly between successive rounds, if random starting points are used. In order to facilitate the convergence of θ, we always use to initialize a search in the nth round. This modification greatly improves the stability of the θ series. The iterative EM algorithm keeps refining θ until the maximum number of rounds (10 by default) is reached (see Supplementary information for data on convergence assessment).

2.3.2 Confidence intervals

The confidence interval for each parameter in the θ vector is computable too. It can be proved that the θ generated by BEESEM is both asymptotically unbiased and asymptotically normal (Rice, 2007). Thus we can assume that θ obeys a multivariate normal distribution, namely , where λ is the mean vector and Σ represents the covariance matrix. Since Equation (4) gives an (asymptotically) unbiased estimate of λ, the only unknown parameter of the multivariate normal distribution is Σ. The covariance matrix is related to the Hessian matrix of the objective function in Equation (4). To proceed, we assume that the measurement errors of R_j are independent and obey the same normal distribution $N(0,{\sigma }^2)$. ${\sigma }^2$ can be estimated using the sum of squared residuals, which equals to the value of the objective function at θ. If $R_j(\mathit{\theta })$, namely the RHS of Equation (4), is linear with respect to θ, it can be shown that (Rice, 2007)

$$\Sigma ={\sigma }^2{\mathbf{H}}^{-1}.$$ (5)

In this equation, H represents the Hessian matrix of the objective function. Although $R_j(\mathit{\theta })$ is actually a nonlinear function with respect to θ, we can assume that the objective function is well approximated by a parabola in the vicinity of a minimum (namely the Laplacian approximation). This approximation enables us to compute the confidence intervals using second order derivatives, which means Equation (5) still holds.

2.3.3 Motif length selection

BEESEM can infer the optimal motif length if a user-defined value is not supplied. To optimize the motif length, BEESEM first generates a series of energy PWMs, ranging from 7 to 10 bp. Then the candidate PWM that contains the k-mer submatrix (k defaults to 5) with the highest MCIC is identified and it is called the core PWM. Next, BEESEM collects any candidate PWM that meets the following three criteria: (i) it is longer than the core PWM, (ii) one of its k-mer submatrices is highly correlated with any submatrix in the core PWM and (iii) it does not contain a non-informative position at either end. A non-informative position is a PWM column with low information content (less than 0.25 bit by default). Finally, BEESEM chooses the longest one from the collected PWMs (including the core PWM).

2.3.4 Types of BEESEM PWMs

We generated a total of 660 PWMs by applying BEESEM to the aforementioned HT-SELEX datasets. Each BEESEM PWM comes in two types: seeded and unseeded. When generating seeded PWMs, BEESEM uses the consensus sequences of the J2013 PWMs as starting points (initial guesses). The unseeded PWMs, by contrast, were estimated without any prior knowledge of the motifs (see Supplementary information for details). The percentages of 7, 8, 9 and 10 bp seeded PWMs are 24%, 23%, 30% and 23% respectively. The corresponding percentages for unseeded PWMs are 27%, 19%, 31% and 23% respectively.

2.4 Evaluation

We evaluated the BEESEM PWMs on HT-SELEX data, as well as PBM and ChIP-seq data from independent experiments. In addition, we compared their performance in the evaluation tests with 5 other binding models, including the J2013 PWMs, HTS-IBIS, DiMO, BEEML and DeepBind. HTS-IBIS is derived from the RAP algorithm (Orenstein et al., 2013) and optimized for HT-SELEX data. The HTS-IBIS PWMs were generated by applying the HTS-IBIS program to the HT-SELEX datasets used in this study. DiMO is based on perceptron learning (Patel and Stormo, 2014) and aims to maximize the AUC score of a PWM based on ChIP-seq data. To generate a DiMO PWM, we initialize DiMO with a J2013 PWM and then train it on the ChIP-seq data of the corresponding TF. BEEML is a motif finding algorithm built on a biophysical model of protein–DNA interactions, and the corresponding PWMs were trained on PBM data (Zhao and Stormo, 2011), using a specialized version of BEEML for PBM data (BEEML-PBM). DeepBind uses deep learning to train binding models on in vitro and in vivo data, including HT-SELEX data. The DeepBind binding models were trained on HT-SELEX data and published in Alipanahi et al. (2015). The BEEML PWMs are not evaluated on ChIP-seq data, because few TFs have both BEEML PWMs and ChIP-seq data. For similar reasons, the DiMO PWMs are not evaluated on PBM data.

In the HT-SELEX evaluation tests, we tested the internal consistency of the HT-SELEX based methods and their abilities to accurately model the results of the HT-SELEX experiments. We developed two methods for evaluating binding models on HT-SELEX data, which are called the ‘consistency’ test and the ‘goodness-of-fit’ test respectively. In both methods, the assessment is based on the difference between two computed sequence distributions, which should be the same under an accurate specificity model. The difference can be measured in two ways: the square of the Pearson’s r (denoted by r²) and the symmetric divergence (denoted by $D_{\text{sym}}$). The symmetric divergence, with a minimum value of 0 that indicates a perfect fit, is derived from the Kullback–Leibler divergence (Kullback and Leibler, 1951). In the consistency test, we assess the difference between two predicted binding site distributions, namely two predictions of the $P(s_j|B)$ in Equation (2). The two distributions are computed with different approaches: one is calculated using the PWM and the sequencing dataset before TF binding, and the other is calculated using the PWM and the dataset after TF binding. Since both approaches require a presumptive PWM, the resulting distributions are both theoretical predictions. Notwithstanding, we expect the two distributions to be similar, if the binding model is consistent. In the goodness-of-fit test, we assess the difference between two after-binding (overall) m-mer distributions. One distribution is calculated directly using the sequencing dataset after TF binding, thus representing the empirical distribution. The other is theoretical and can be calculated using the PWM and the dataset before TF binding (see Supplementary information for details). If the binding model is accurate, the predicted distribution should agree with the empirical one.

In the PBM evaluation tests, we tested the ability of the HT-SELEX based methods to predict PBM data. PBMs are an independent in vitro experiment, so this is an important external validation. In the PBM test, we evaluate the ability of a binding model to predict the in vitro affinities of PBM probes, as measured by their fluorescence intensities. The PBM datasets generated by multiple studies were retrieved from the CIS-BP database (cisbp.ccbr.utoronto.ca) (Weirauch et al., 2014). These datasets include both mouse and human TFs. To evaluate a binding model, we use it to calculate the average affinity score of all the m-mers on each PBM probe (including the reverse complement), where m represents the motif length and depends on the binding model. The correlation between the predicted scores and the probe intensities, as measured by the square of the Pearson’s r, is used for evaluating the binding models.

In the ChIP-seq evaluation tests, we assessed how well the BEESEM PWMs, which are trained on HT-SELEX data, could identify in vivo TF binding sites. Here, we use the ChIP-seq data from the ENCODE project database (www.encodeproject.org) (Landt et al., 2012) and the ROC curve to quantify the ability of binding models to identify ChIP-seq peaks among random DNA sequences (Orenstein and Shamir, 2014). To perform the evaluation test, we first rank all the peaks in a ChIP-seq dataset based on their enrichment scores. Then we retrieve the center sequences of the top 500 peaks, which are all 250 bp long, and treat them as the positive sequence set (as in Orenstein and Shamir, 2014). To generate the negative set, we collect the DNA sequence 200 bp downstream from each positive sequence. Next, we assign an affinity score to each sequence. The affinity score of a sequence is defined as the highest affinity of its constituent m-mers (including the reverse complement), where m is the motif length and depends on the binding model. Finally, we rank all the sequences based on their affinity scores, plot the ROC curve, and compute the AUC score.

3 Results

3.1 Characterization of BEESEM PWMs

3.1.1 Reproducibility

The reproducibility of an BEESEM PWM can be measured by its standard deviation or the confidence intervals of its elements. In this study, the standard deviation of a PWM is defined as the mean of the standard deviations of its elements, which can be individually estimated using the covariance matrix of θ. Although the confidence interval is a more natural way to quantify the uncertainty in an estimate, we focus on the standard deviation for two reasons. First, the two measures are equivalent if the estimate obeys a normal distribution, as in our case. Second, it is difficult to summarize the confidence intervals of multiple estimates, while it is straightforward to average their standard deviations. The average standard deviations of seeded and unseeded BEESEM PWMs are 0.014 and 0.015 respectively. The standard deviations are very small compared with the absolute values of PWM elements, averaging 1.73 for seeded and 1.76 for unseeded PWMs. Thus we consider the estimated binding energies to be highly reproducible.

3.1.2 Information content

The average MCIC of seeded and unseeded BEESEM PWMs is 0.58 bit and 0.60 bit respectively. They are both smaller than the average MCIC of the corresponding J2013 PWMs, which is 1.19 bit. Thus the BEESEM PWMs are generally less specified than the J2013 PWMs. It was reported that motifs with lower MCIC often fit quantitative binding data better (Weirauch et al., 2013).

3.2 Motif evaluation

3.2.1 Evaluation on HT-SELEX data

Table 1 shows the evaluation results for BEESEM, BEEML, HTS-IBIS, the J2013 PWMs and DiMO on HT-SELEX data. The BEESEM PWMs on average achieve better scores than the other algorithms in both the consistency and the goodness-of-fit tests, by either the r² or the $D_{\text{sym}}$ criterion. Based on the two-sided T-test, the difference in the consistency r² between the unseeded BEESEM PWMs and BEEML ($P\text{‐value}=1.8\times {10}^{-5}$), HTS-IBIS ($P\text{‐value}=1.7\times {10}^{-47}$), J2013 ($P\text{‐value}=6.6\times {10}^{-48}$), DiMO ($P\text{‐value}=3.0\times {10}^{-29}$) is significant. The difference in the goodness-of-fit r² between the unseeded BEESEM PWMs and HTS-IBIS ($P\text{‐value}=1.3\times {10}^{-15}$), J2013 ($P\text{‐value}=2.0\times {10}^{-19}$), DiMO ($P\text{‐value}=4.7\times {10}^{-12}$) is significant, but not for BEEML ($P\text{‐value}=0.089$). It is noteworthy that there is only a small difference in performance between the two BEESEM PWM types (the P-value for the consistency and goodness-of-fit r² is 0.88 and 0.77 respectively). The DiMO PWMs significantly lag behind the other algorithms presumably because DiMO overfits the characteristics of the ChIP-seq data that it was trained on. Column-wise comparisons show that the r² of a goodness-of-fit test is generally lower than the corresponding consistency test, which is consistent with the goodness-of-fit test being more stringent, although the $D_{\text{sym}}$ is better on the goodness-of-fit test. The Supplementary information contains more comparisons of the motifs and the overall performance of BEESEM, HTS-IBIS and other methods.

Table 1.

The results of the HT-SELEX evaluation tests

Algorithm	Number of PWMs	Consistency r2 (s.d.)	Consistency $D_{\text{sym}}$ (s.d.)	Goodness-of-fit r2 (s.d.)	Goodness-of-fit $D_{\text{sym}}$ (s.d.)
BEESEM seeded	660	0.79 (0.26)	0.46 (0.48)	0.47 (0.26)	0.40 (0.31)
BEESEM unseeded	660	0.79 (0.27)	0.49 (0.50)	0.46 (0.26)	0.43 (0.35)
BEEML	76	0.65 (0.28)	0.90 (0.80)	0.41 (0.29)	0.50 (0.32)
HTS-IBIS	660	0.55 (0.30)	2.60 (1.26)	0.35 (0.22)	1.23 (0.52)
J2013	660	0.53 (0.35)	3.86 (2.49)	0.33 (0.26)	1.63 (0.93)
DiMO	73	0.39 (0.33)	28.3 (23.1)	0.24 (0.22)	5.52 (3.14)

Note: There are fewer DiMO or BEEML PWMs because only a subset of the TFs have ChIP-seq or PBM data. All the tests are performed using the 2nd SELEX cycle as the prior and the 3rd cycle as the posterior. All the PWMs are trimmed to 8 bp in order for direct comparison. The best score in each column is boldfaced. Scores that are not significantly different from the best scores are italicized (P-value). DeepBind is excluded from the HT-SELEX test because the output of its models cannot be interpreted as simple binding probabilities. Additional test results can be found in the Supplementary information.

3.2.2 Evaluation on PBM data

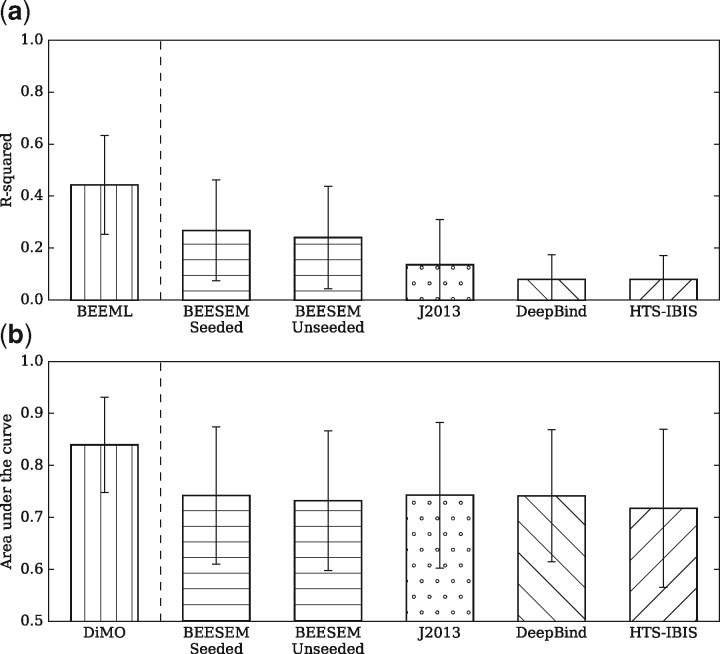
The mean r² achieved by each motif finding algorithm in the PBM evaluation tests is shown in Figure 2a. In this comparison, the BEEML PWMs are a positive control because they were trained on PBM data. The real assessment is how the HT-SELEX based methods (BEESEM, J2013, DeepBind and HTS-IBIS) can predict the PBM data. Because the PBM test is an independent validation for the HT-SELEX based methods, their r² scores in Figure 2a are generally lower than the corresponding goodness-of-fit r² in Table 1. Compared with the other methods, the seeded and unseeded BEESEM PWMs are ranked first and second respectively, with a mean r² of 0.27 and 0.24, and approach the performance of the positive control ($r^2=0.44$). Based on the two-sided T-test, the difference between the seeded and unseeded BEESEM PWMs is not significant (P-value=  0.42). The remaining three algorithms (J2013: 0.14, HTS-IBIS: 0.08 and DeepBind: 0.08) achieve much lower r², compared with BEEML and BEESEM. The difference between the unseeded BEESEM PWMs and J2013 ($P‐\text{value}=0.0014$), DeepBind ($P‐\text{value}=1.5\times {10}^{-8}$), HTS-IBIS ($P‐\text{value}=1.3\times {10}^{-8}$) is significant.

Fig. 2.

The results of the PBM and ChIP-seq evaluation tests. (a) In the PBM tests, the number of binding models tested is 67 for each algorithm. The error bars mark the standard deviation of the scores. The BEEML bar is singled out because the corresponding PWMs were trained on PBM data. For the other binding models trained on HT-SELEX data, the PBM test is an external validation on in vitro data. (b) In the ChIP-seq tests, the number of binding models tested is 72 for each algorithm. The error bars mark the standard deviation of the scores. The y axis starts from 0.5, the expected score of a random classifier. The DiMO bar is singled out because the corresponding PWMs were trained on ChIP-seq data. For the other binding models trained on HT-SELEX data, the ChIP-seq test is an external validation on in vivo data

3.2.3 Evaluation on ChIP-seq data

The performance of each motif finding algorithm in the ChIP-seq evaluation tests, as measured by the mean AUC score, is shown in Figure 2b. The results show that the DiMO PWMs achieve the highest average AUC score (0.84). This is mainly because these PWMs were trained on the same ChIP-seq data used for evaluation, while all the other motifs were trained on HT-SELEX data. In addition DiMO is designed to maximize the AUC score of a PWM, the same as our evaluation criterion. The seeded BEESEM PWMs, the J2013 PWMs and the DeepBind models all achieve a mean AUC score of 0.74, whereas the unseeded BEESEM achieves 0.73 and HTS-IBIS achieves 0.72 (similar to the result reported in Orenstein and Shamir, 2015). Based on the two-sided T-test, there is no significant difference among the algorithms trained on HT-SELEX data.

4 Discussion

BEESEM infers the specificity of TFs based on HT-SELEX data by extending our previous development of BEEML (Stormo and Zhao, 2010). BEESEM allows the sequences to be much longer than the binding sites, which requires the simultaneous estimation of the binding site locations and the specificity model. This general problem was addressed using the EM algorithm (Lawrence and Reilly, 1990), but in that case the data consisted simply of a collection of sequences containing sites without quantitative binding information. Now we include the enrichment of sites by comparing the posterior distribution to the prior (the distribution before the binding site selection). This requires nonlinear parameter estimation as part of the EM maximization step. We previously showed that standard motif finding algorithms, that don’t account for the ratios of the posterior to the prior distributions and that don’t apply nonlinear parameter estimation, perform much less well even on relatively simple datasets (Stormo and Zhao, 2010). We also use the EM algorithm to filter out low-affinity sequence reads that are carried over from the previous SELEX cycle and thus do not contain any high-affinity binding site. In fact, both the seeded and unseeded BEESEM PWMs predict that on average only 60% of the sequence reads actually contain a binding site. We are still employing some approximations, such as the PWM model of specificity (Weirauch et al., 2013; Zhao and Stormo, 2011) and assuming each sequence is bound by at most one protein, but we expect these do not have large effects on the models.

The estimation of the binding site location is important because of the very large libraries from which the selections are made. A library of random 20-mers contains over 10¹² different sequences, well beyond the capacity of current sequencing approaches. In fact essentially all of the sequences in the initial pool are unique. Even after four rounds of selection the most abundant 20-mer usually occurs between 10–100 times. In a 20-mer library, every 10-mer occurs in more than 10⁷ different contexts so that even if selection was very stringent, most selected and sequenced sites would be unique. By focusing on typical motif lengths, 7–10 bp, and summing over their occurrences in both the prior and posterior distributions, we can obtain models with good fits to the selection data.

Despite the clear improvements in modeling the in vitro quantitative binding data (both HT-SELEX and PBM), the BEESEM motifs achieve essentially equal AUC scores in the ChIP-seq test, which is a valuable independent assessment but also has limitations. Certainly an important use of motifs is in predicting binding events in vivo, and also in accounting for changes in expression that are correlated with genetic variants (Zheng et al., 2011). The AUC criterion has been cited previously as a method for evaluating the quality of motifs determined from in vitro binding data (Orenstein and Shamir, 2014; Weirauch et al., 2013). But ROC curves, and the AUC measures based on them, have important limitations. First, there are biological considerations. Binding of TFs in vivo is confounded by a myriad of other proteins, including nucleosomes, that compete or cooperate in binding. In addition, defining an appropriate negative sequence set is challenging. Ideally these would be genomic regions that are accessible for the TF to bind, but to which it does not under conditions in which it does bind to the positive dataset, but that criterion is seldom used. Second, ROC curves are intrinsically rank-based. The scores assigned to each peak, predicted binding energies in our case or log-probabilities when using probabilistic models, can be multiplied by any constant without altering the ROC curve, and the AUC measurement. In fact, the J2013 motifs, which perform well in the ChIP-seq test, have very high information content. We had previously suggested, based on comparisons with different high-throughput methods, that the J2013 algorithm for HT-SELEX was producing over-specified motifs (Gupta et al., 2014). It was observed for PBM data that algorithms that generated higher information content motifs tended to fit the quantitative binding data less well (Weirauch et al., 2013). Finally, our results using the DiMO method of motif optimization are enlightening. We reasoned that if the AUC is a good criterion for evaluating a motif on ChIP-seq data, one could use it as the objective function for motif optimization. Using a simple perceptron algorithm we showed that nearly any motif, obtained by a variety of motif discovery algorithms on ChIP-seq data, could be modified to increase its AUC score (Patel and Stormo, 2014). When applying DiMO to the ChIP-seq datasets analyzed in this work, and using the J2013 motifs as starting points, we could in every case obtain a new motif with a higher AUC score. This was accompanied by an increase in MCIC. However, those DiMO motifs perform significantly worse on the quantitative HT-SELEX data and are further over-specified, highlighting the limitation of using the AUC as the sole criterion for evaluating motif quality.

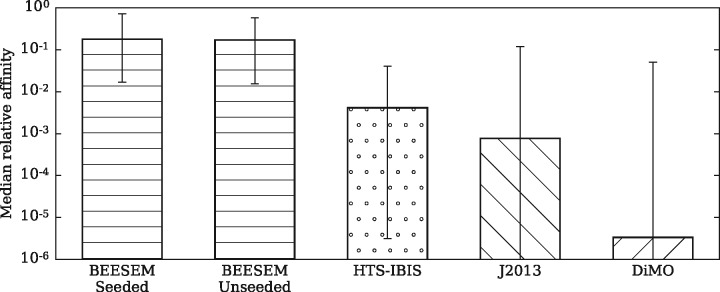
To gain more insights into the ChIP-seq test, we assess each binding model using the median relative affinity (MRA) of each ChIP-seq dataset, which is defined as the median affinity score of the top 500 peaks divided by their highest affinity score. Figure 3 shows that the median MRA for the BEESEM PWMs is about 0.2 while the other binding models predict very low MRAs (their median MRAs are all less than 0.005). It means J2013, DiMO and HTS-IBIS generally predict a >200-fold affinity difference between the peak of the highest affinity and the median peak. Although the true differences in the relative affinity for the different peaks are unknown, it seems unlikely that half of the binding sites in these top scoring peaks would have such low binding affinities. In fact changes in binding affinity of 10-fold are often considered deleterious when inferring causal variants responsible for changes in gene expression (Kasowski et al., 2010; Reddy et al., 2012).

Fig. 3.

The median relative affinities (MRAs) predicted by different binding models. The number of PWMs tested is 73 for each algorithm. The rectangular bars mark the 50th percentile (the median) of the 73 MRAs for each algorithm, and the error bars mark the 5th and 95th percentiles. DeepBind is excluded from the HT-SELEX test because the output of its models cannot be interpreted as simple binding probabilities

We consider the fit to in vitro binding data to be the best criterion for judging the quality of TF binding motifs. The in vitro data measure intrinsic binding specificity without the confounding effects that occur in vivo. When obtained over a wide range of affinities, either HT-SELEX or PBM data can provide good quantitative models of specificity. The ROC curves are still of value, but should not be the primary means of evaluation. Low AUC values can point to important information that is missing from the models of intrinsic specificity alone. For example, a highly enriched ChIP-seq peak without a high-affinity binding site may indicate indirect binding, although a low-affinity site that is bound cooperatively with another factor seems more likely. In general, reliable specificity models, which are most easily obtained in vitro, are the most useful information for understanding regulatory sites in vivo and the alterations in gene regulation that occur in genetic variants. In particular, accurate relative affinity estimates for genetic variants are useful for distinguishing likely deleterious variants from fairly benign ones.