Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2017 Oct 4;34(4):695–697. doi: 10.1093/bioinformatics/btx626

PyDREAM: high-dimensional parameter inference for biological models in python

Erin M Shockley 1, Jasper A Vrugt 2,3, Carlos F Lopez 1,✉
Editor: Alfonso Valencia
PMCID: PMC5860607  PMID: 29028896

Abstract

Summary

Biological models contain many parameters whose values are difficult to measure directly via experimentation and therefore require calibration against experimental data. Markov chain Monte Carlo (MCMC) methods are suitable to estimate multivariate posterior model parameter distributions, but these methods may exhibit slow or premature convergence in high-dimensional search spaces. Here, we present PyDREAM, a Python implementation of the (Multiple-Try) Differential Evolution Adaptive Metropolis [DREAM(ZS)] algorithm developed by Vrugt and ter Braak (2008) and Laloy and Vrugt (2012). PyDREAM achieves excellent performance for complex, parameter-rich models and takes full advantage of distributed computing resources, facilitating parameter inference and uncertainty estimation of CPU-intensive biological models.

Availability and implementation

PyDREAM is freely available under the GNU GPLv3 license from the Lopez lab GitHub repository at http://github.com/LoLab-VU/PyDREAM.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Mechanistic models of biological processes are widely used to study and explain observed cellular behaviors and generate testable hypotheses for experimental validation (Chylek, 2015; Eydgahi, 2013; Janes and Lauffenburger, 2013; Neumann, 2010; Shankaran, 2012; Suderman and Deeds, 2013). As model complexity increases, the number of unknown parameters may increase manyfold making their calibration against experimental data increasingly challenging (Eydgahi, 2013; Klinke, 2009). Although several authors have advocated the use of ensemble methods for parameter estimation purposes (Brown and Sethna, 2003; Klinke, 2009), optimization methods remain widely used in quantitative biology, largely due to the computational challenges associated with parameter inference in commonly available computing environments (Neumann, 2010; Thomas et al., 2015). In recent years, Bayesian methods have found widespread application and use for ensemble parameter estimation in fields including systems biology (Eydgahi, 2013), hydrology (Schoups and Vrugt, 2010), astrophysics (Bovy, 2012) and many others (Vrugt, 2016). These methods rely on Bayes’ theorem to determine the posterior density of the model output and use Markov chain Monte Carlo (MCMC) simulation to approximate the posterior parameter distribution. The earliest MCMC approach is the random walk Metropolis (RWM) algorithm which generates a random walk through the parameter space and successively visits solutions with stable frequencies stemming from a stationary distribution. The sampled points are collected in a Markov chain and used to summarize the posterior parameter distribution and related moments. The MCMC approach has led to useful biological insights (Eydgahi, 2013; Klinke, 2009) but is difficult to execute in practice as the number of samples required to achieve convergence may be prohibitive, particularly when the chain’s transition density (proposal distribution) poorly approximates the actual target distribution. In the past decades, many different adaptation strategies of the proposal distribution have been developed to enhance the convergence rate of the sampled chain(s) (Andrieu and Thoms, 2008; Vrugt, 2016).

Here we present PyDREAM, a Python toolbox of two MCMC methods of the DiffeRential Evolution Adaptive Metropolis (DREAM) family of sampling algorithms (Laloy and Vrugt, 2012; Vrugt, 2009, 2016; Vrugt and ter Braak, 2008). In particular, our package includes the DREAM(ZS) (Vrugt, 2016; Vrugt and ter Braak, 2008) and the MT-DREAM(ZS) (Laloy and Vrugt, 2012) MCMC algorithms, and considerably simplifies parameter inference for complex biological systems. Both methods use a common multi-chain architecture and create (multivariate) candidate points in each chain on the fly via differential evolution, (Price, 2005; Storn and Price, 1997) using a multiple of the difference between one or more pairs of past states of the joint chains as a jump vector (ter Braak, 2006). Periodically, this parallel direction jump is replaced by a snooker jump to diversify the candidate points (Vrugt and ter Braak, 2008). Both these steps equate to a discrete and adaptive proposal distribution with scale and orientation of the jump vector that conforms rapidly to the target distribution en route of the sampled chains to their stationary distribution (ter Braak, 2006). By accepting each multivariate jump (candidate point) with the Metropolis ratio, a Markov chain is obtained whose stationary distribution is equivalent to the target distribution, maintains detailed balance, and shows increased performance in multimodal search problems. The MT-DREAM(ZS) algorithm is an extension of the DREAM(ZS) algorithm designed to accelerate the chains’ convergence rate for CPU-demanding parameter-rich models. This scheme generates multiple different candidate points in each chain using a parallel direction and snooker jump implementation of the so-called MTM(II) variant of Liu (2000). It has been successfully applied to models with hundreds of parameters in fields such as hydrology (Laloy and Vrugt, 2012). We refer interested readers to Vrugt (2016) for a discussion of adaptive single and multichain MCMC methods and for a detailed review and MATLAB implementation of the DREAM family of algorithms.

The DREAM(ZS) and MT-DREAM(ZS) algorithms are amenable to a multi-threaded computing implementation in which the chain’s candidate points are evaluated simultaneously in parallel using distributed architectures. This significantly reduces the required CPU budget and makes high-dimensional parameter inference more tractable. Below, we detail our PyDREAM toolbox and illustrate its use with a simple biological example. We refer readers to the Supplemental Material for a more exhaustive introduction to Bayesian inference and MCMC simulation, and detailed description of our Python package, including several example applications. PyDREAM is distributed under the GNU GPLv3 open-source license and is made freely available through GitHub and the Python package Index (PyPI) for community development and general access.

2 Implementation

PyDREAM has been implemented in the Python programming language and takes full advantage of Python’s multiprocessing capabilities to facilitate distributed multi-core evaluation of the candidate points. Through the wider Python ecosystem, PyDREAM can access many other packages and functionalities such as programmatic rule-based model management (PySB) (Lopez et al., 2013), SciPy (numerical simulation and analysis; http://www.scipy.org) and matplotlib (graphics) (see Supplementary Material for examples). The PyDREAM toolbox has been tested exhaustively to make sure that the output of the Python implementation matches the results of the MATLAB packages of DREAM(ZS) and MT-DREAM(ZS) (see Supplementary Figures 7 and 8). PyDREAM can be installed by typing pip install pydream from the command line.

3 Results

3.1 Example problem

We now illustrate the application of PyDREAM to parameter estimation of the COX-2 Reaction Model (CORM) (Mitchener, 2015). A more detailed explanation of this case study with additional figures is provided in the Supplementary Material. CORM includes the catalytic and allosteric interactions of the enzyme cyclooxygenase-2 (COX-2) with two of its substrates, arachidonic acid (AA) and 2-arachidonoyl glycerol (2-AG). The two substrates are converted into prostaglandin (PG) and prostaglandin-glycerol (PGG), respectively. The model involves 13 species and 29 reactions. We assume the following to be known a priori: (i) the plausible biological interactions in the system, (ii) experimentally measured rate constants for some of these interactions, (iii) the amount of enzyme and substrate(s) present in any given experiment, (iv) experimental measurements of the products PG and PGG at a variety of initial substrate concentrations and (v) biologically plausible ranges for the unmeasured rate parameters. We then wish to determine the values of the unknown rate parameters that satisfy our stipulated prior knowledge. This equates to inference of the posterior distribution of the rate parameters, and involves three general steps with PyDREAM: (i) specification of the prior parameter distribution, (ii) selection of an appropriate likelihood function and (iii) MCMC simulation. An overview of each step as applied to the CORM example is provided below with greater detail available in the Supplementary Material. In addition to the CORM example, the PyDREAM package includes three additional case studies involving two multivariate statistical distributions and a simple biochemical model.

3.2 Parameter priors

In a Bayesian context, the prior distribution encodes all our ‘subjective’ knowledge about the parameters, before collection of the experimental data. This distribution, often simply called the prior, expresses one’s beliefs about the parameters before the data (also referred to as evidence) is taken into account. Because CORM is a model of biochemical interactions, the prior parameter distribution were selected based on expert knowledge about biologically plausible kinetic rate values. CORM contains two types of experimental parameters: disassociation constants for the interactions of COX-2 with its substrates and catalytic constants for turnover of different enzyme-substrate species. In the absence of detailed knowledge of these disassociation and catalytic constants, we adopted marginal normal priors that span millimolar to nanomolar affinity for disassociation constants and from 0.01 s−1 to 100 s−1 for rate constants. PyDREAM uses the SciPy (Jones, 2001) package to define a host of different univariate and multivariate prior distributions (e.g. normal, uniform). Other prior distributions can also be defined by the user (Supplemental Material, Section 7.1).

3.3 Likelihood function

In a Bayesian context, the likelihood function summarizes in probabilistic terms the distance between the experimental data and the simulated results (of a given model parameter vector). In PyDREAM, we use a separate Python function to compute the log-likelihood of each multidimensional parameter vector. This function requires the measured experimental data as input, and may include constraints or other ‘soft’ and hard data to better evaluate the likelihood of each simulated model output. For CORM, the likelihood function quantifies, in probabilistic terms, the agreement between the observed and simulated concentrations of the products PG and PGG, respectively. It is also assumed that the experimental measurements are normally distributed with a standard deviation calculated from multiple measurements. Furthermore, CORM’s likelihood function promotes (via a constraint) energy conservation in all thermodynamic cycles simulated by the model. The code for the CORM likelihood function is included in the Supplementary Material, along with other likelihood functions.

3.4 Sampling

After formulation of the prior parameter distribution and the likelihood function, PyDREAM generates samples from the target distribution, carrying out MCMC parameter space exploration with the (MT)-DREAM(ZS) algorithm. Sampling with PyDREAM requires calling a single function and passing the defined parameter priors and likelihood function as argument inputs. The function returns an array of sampled states for each of the chains and the associated posterior probability density of each parameter vector. Various convergence criteria, which are needed to determine the necessary burn-in before the joint chains reach a stationary distribution, can then be calculated. Convergence of the sampled trajectories can also be assessed visually, by inspecting the mixing of the individual chains, but this assessment could be subjective, particularly in high-dimensional parameter spaces with complex multivariate dependencies among the parameters. The marginal, bivariate and joint posterior distributions can be plotted using a Python package of choice such as matplotlib, or the stationary samples may be exported in the CSV format for further analysis. For example, Figure 1 presents histograms of the marginal posterior distribution of two CORM parameters. Convergence was achieved within ten thousand model evaluations, requiring less than an hour to complete on a six-core processor. This is over one order of magnitude faster than a single chain, non-adaptive, MCMC method.

Fig. 1.

Fig. 1

Open in a new tab

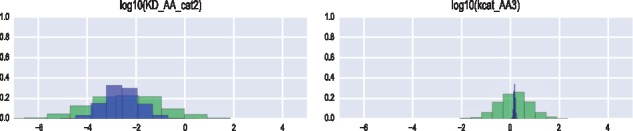
Histogram of the prior (green) and posterior (blue) distributions of two parameters of the COX-2 Reaction Model

4 Summary

We present PyDREAM, a Python, open-source implementation of the DREAM(ZS) and MT-DREAM(ZS) sampling algorithms for efficient inference of complex, high-dimensional, posterior parameter distributions. The toolbox builds on the MATLAB DREAM package and is available at the Lopez lab GitHub repository (http://github.com/LoLab-VU/PyDREAM).

Supplementary Material

Supplementary Data
Click here for additional data file. (2.4MB, pdf)

Acknowledgements

We would like to thank: Dr Christopher Fonnesbeck for advice throughout the implementation of this method; Dr Lawrence Marnett and Michelle Mitchener for experimental data and insights; Dr Alexander L.R. Lubbock for advice in the implementation of the code and the content of this manuscript; Dr Blake A. Wilson for feedback regarding manuscript content.

Funding

This work was supported by the National Science Foundation under Grant [MCB-1411482]; NIH Grant [5T32GM065086 to E.M.S.]. This research used resources of the Oak Ridge Leadership Computing Facility, supported by the Office of Science of the US Department of Energy under Contract DE-AC05-00OR22725.

References

  1. Andrieu C., Thoms J. (2008) A tutorial on adaptive MCMC. Stat. Comput., 18, 343–373. [Google Scholar]
  2. Bovy J. et al. (2012) The spatial structure of mono-abundance sub-populations of the Milky Way disc. Astrophys. J., 753, 148. [Google Scholar]
  3. Brown K.S., Sethna J.P. (2003) Statistical mechanical approaches to models with many poorly know parameters. Phys. Rev. E, 68, 021904. [DOI] [PubMed] [Google Scholar]
  4. Chylek L.A. et al. (2015) Modeling for (physical) biologists: an introduction to the rule-based approach. Phys. Biol., 12, 4.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Eydgahi H. et al. (2013) Properties of cell death models calibrated and compared using Bayesian approaches. Mol. Syst. Biol, 9, 644.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Janes K.A., Lauffenburger D.A. (2013) Models of signalling networks—what cell biologists can gain from them and give to them. J. Cell. Sci., 126, 1913–1921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jones E. et al. (2001) SciPy: Open Source Scientific Tools for Python.
  8. Klinke D.J. (2009) An empirical Bayesian approach for model-based inference of cellular signaling networks. BMC Bioinformatics, 10, 371.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Laloy E., Vrugt J.A. (2012) High-dimensional posterior exploration of hydrologic models using multiple-try DREAMZS and high-performance computing. Water Resour. Res., 48, W01526. [Google Scholar]
  10. Liu J. et al. (2000) The multiple-try method and local optimization in Metropolis sampling. J. Am. Stat. Assoc., 95, 121–134. [Google Scholar]
  11. Lopez C.F. et al. (2013) Programming biological models in Python using PySB. Mol. Syst. Biol., 9, 646.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Mitchener M.M. et al. (2015) Competition and allostery govern substrate selectivity of cyclooxygenase-2. Proc. Natl. Acad. Sci. USA, 112, 12366–12371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Neumann L. et al. (2010) Dynamics within the CD95 death-inducing signaling complex decide life and death of cells. Mol. Syst. Biol., 6, 352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Price K. et al. (2005) Differential Evolution: A Practical Approach to Global Optimization. Springer-Verlag, Berlin Heidelburg. [Google Scholar]
  15. Schoups G., Vrugt J.A. (2010) A formal likelihood function for parameter and predictive inference of hydrologic models with correlated, heteroscedastic, and non-Gaussian errors. Water Resour. Res., 46, W10531. [Google Scholar]
  16. Shankaran H. et al. (2012) Integrated experimental and model-based analysis reveals the spatial aspects of EGFR activation dynamics. Mol. BioSyst., 8, 2868–2882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Storn R., Price K. (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim., 11, 341–359. [Google Scholar]
  18. Suderman R., Deeds E.J. (2013) Machines vs. ensembles: effective MAPK signaling through heterogeneous sets of protein complexes. PLoS Comput. Biol., 9, e1003278.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. ter Braak C.J.F. (2006) A Markov Chain Monte Carlo version of the genetic algorithm differential evolution: easy Bayesian computing for real parameter spaces. Stat. Comput., 16, 239–249. [Google Scholar]
  20. Thomas B.R. et al. (2015) BioNetFit: a fitting tool compatible with BioNetGen, NFsim, and distributed computing environments. BMC Bioinformatics, 32, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Vrugt J.A., ter Braak C.J.F. (2008) Differential evolution Markov chain with snooker updater and fewer chains. Stat. Comput, 18, 435–446. [Google Scholar]
  22. Vrugt J.A. et al. (2009) Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci., 10, 271–288. [Google Scholar]
  23. Vrugt J.A. (2016) Markov chain Monte Carlo simulation using the DREAM software package: theory, concepts, and MATLAB implementation. Environ. Modell. Softw., 75, 273–316. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
Click here for additional data file. (2.4MB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES