Predicting Length of Stay for Obstetric Patients via Electronic Medical Records

Abstract

Obstetric care refers to the care provided to patients during ante-, intra-, and postpartum periods. Predicting length of stay (LOS) for these patients during their hospitalizations can assist healthcare organizations in allocating hospital resources more effectively and efficiently, ultimately improving maternal care quality and reducing costs to patients. In this paper, we investigate the extent to which LOS can be forecast from a patient’s medical history. We introduce a machine learning framework to incorporate a patient’s prior conditions (e.g., diagnostic codes) as features in a predictive model for LOS. We evaluate the framework with three years of historical billing data from the electronic medical records of 9188 obstetric patients in a large academic medical center. The results indicate that our framework achieved an average accuracy of 49.3%, which is higher than the baseline accuracy 37.7% (that relies solely on a patient’s age). The most predictive features were found to have statistically significant discriminative ability. These features included billing codes for normal delivery (indicative of shorter stay) and antepartum hypertension (indicative of longer stay).

Introduction

Electronic medical record (EMR) systems have been widely adopted in the United States (US) and abroad [1–4]. These systems enable a substantial amount of data to be captured during the routine practice of healthcare organizations (HCOs) [2–5]. This information is quite heterogeneous, including structured diagnoses, medication regimens, laboratory test results and vital signs, as well as un- or semi-structured clinical narratives. The data stored in EMRs is increasingly recognized for its ability to support numerous activities, such as clinical decision making [6], patient safety improving [7–8] and discovery-driven biomedical research [2–4].

Currently, some of the most challenging healthcare environments to manage for safety are those associated with maternity. Over the past several decades, the maternal mortality ratio (MMR) has risen dramatically in the US. MMR has doubled from 7.2 deaths of mothers per 100,000 live births in 1987 to 14 in 2015 [9]. At the same time, obstetric care is the most common and costly type of hospital care for all payers in the US [10–12]. Prediction of the length of stay (LOS) for obstetric patients during their hospitalization can help unit managers and administrators make decisions about hospital resource allocation - enabling obstetric care improvement before, during and after childbirth. This is notable because better organized care can reduce the morbidity and mortality of women, as well as newborn babies [11;12], while reducing maternity-related costs. The incorporation of an accurate estimate of LOS in counseling discussions may mitigate anxieties over the uncertainty of a hospital stay as well as prepare for discharge to home or elsewhere [13]. This is important both for obstetric patients and their families who often inquire about the expected duration of a hospitalization.

Previous research has focused on characterizing the factors that lead to LOS variation in general. LOS has, for instance, been shown to be influenced by a patient’s demographics (e.g., age), socioeconomic status (e.g., income, education, and occupation), insurance types (e.g., commercial, private, and Medicaid and Medicare) and severity of illnesses [14–16]. LOS has further been shown to be affiliated with HCO-specific factors, such as physicians’ work efficiency [5,17], climate [18] and the availability of professional language interpretation services [19]. However, the complex relationships between these factors further exacerbate the complexity of LOS prediction. Thus, it is challenging to build LOS prediction models that rely solely on expert knowledge and information ascertained at the time of a patient’s admission to a hospital.

In recognition of these limitations, this paper presents a pilot study on the feasibility of a patient’s historical diagnoses, as documented in an EMR, for LOS predictive models. This study is predicated on the hypothesis that LOS is related to a patient’s medical history. To investigate this hypothesis, we study three years worth of historical diagnosis codes (prior to their most recent admission) for patients on an obstetric service at Northwestern Memorial Hospital (NMH) in Chicago, Illinois, USA. Specifically, we extracted EMR data in the form of International Classification of Diseases, ninth revision (ICD-9) [20] codes and designed a machine learning framework to predict LOS. The results indicate that prediction of LOS within 12 hours can be achieved with almost 30% greater accuracy than the baseline model that relies solely on the patient’s demographics at the time of admission. In addition, we show that certain billing codes are statistically significant in their predictive capability, which suggests they are ripe for further investigation and transition into clinical decision support.

Methods

Figure 1 provides the EMR data and analytics workflow adopted for this investigation. First, the ICD-9 codes and LOS for patients are extracted from the EMR. These are subsequently applied to train and test a predictive model. Finally, the most discriminant ICD-9 codes are prioritized and assessed for statistical significance.

Figure 1.

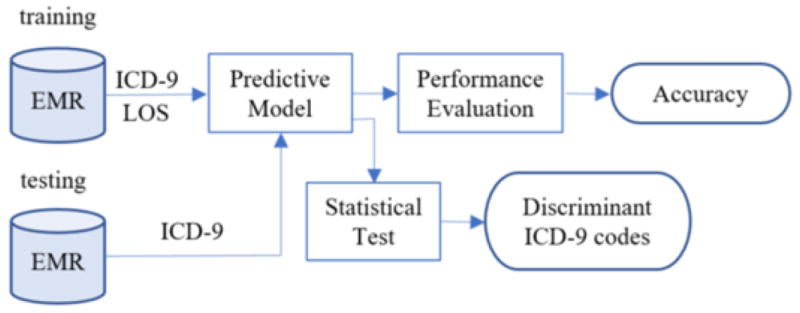
The process by which the LOS predictive model is composed and discriminative features are discovered.

Dataset

The dataset was drawn from the Cerner inpatient EMR system in place at NMH from July 2007 to July 2011. It includes the following patient-specific features: 1) demographics (e.g., age), 2) encounter information (e.g., admission and discharge date), 3) diagnosis (e.g., billing codes) assigned to an encounter, and 4) clinical (e.g., obstetrics) service to which the patient was assigned. In total, there were 9188 inpatients in the dataset with 1849 distinct ICD-9 codes. We consider all inpatients on the obstetric service during 2010–2011 for prediction and rely on EMR data between 2007–2009 as features for our models.

The LOS for an encounter was calculated as the hourly difference between admission and discharge. We use a patient’s age as a baseline prediction for LOS. Table 1 summarizes the average number of ICD-9 codes for the investigated patients in one-, two- and three–years of EMR data, the avarage age of the investigated patients, and the average LOS for these patients on the obstetric service during the 2010–2011 period.

Table 1.

Summary Statistics for ICD-9 codes, age and LOS in the 2010–2011 period

	# of ICD-9 codes			Age	LOS
	1 year	2 years	3 years
Mean	4.3	5.5	6.4	31.8	72
Min	1	1	1	14	1.6
Max	60	80	90	68	1311

The distribution of inpatients on LOS is shown in Figure 2. The LOS for the majority (74%) of obstetric patients ranges from 48 to 96 hours.

Figure 2.

LOS Frequency distribution for study subjects.

Predictive Model

We adopted a random forest model to predict a patient’s LOS according to their historic assigned ICD-9 codes. We rely on a random forest because it is a useful ensemble approach for regression and classification. Specifically, the average LOS from all the trees is used for prediction.

We model the data as a matrix, as shown in Equation (1). Let n be the number of patients and m be the number of unique ICD-9 codes. In this matrix, each row represents a specific patient and each column is a specific characteristic of the patient. The first column is a patient’s LOS (continuous variable) and the rest of the columns are the ICD-9 codes for each patient. To mitigate the influence of repeat visits for patients, we treat each ICD-9 code as a binary variable, such that it is set to 1 if the patient received this diagnosis at least once and 0 otherwise.

$$\left[\begin{array}{ccccc}{\mathit{LOS}}_1& C_1^1& C_1^2& \cdots & C_1^m\\ {\mathit{LOS}}_2& C_2^1& C_2^2& \cdots & C_2^m\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathit{LOS}}_n& C_n^1& C_n^2& \cdots & C_n^m\end{array}\right]$$ (1)

To assess the performance of the approach against traditional practice, we also define a baseline method that leverages age as a single feature in prediction.

Beyond LOS prediction, the importance ranking of features in the predictive model could assist HCOs to apply and interprate the corresponding results. The random forest regression model enables importance ranking for each feature, which is calculated as extent to which prediction error increases when data for the investigated feature is permuted while all others are held constant [21].

Performance Evaluation

A random forest regression predicts an LOS as a continuous value. We evaluated the performance of this prediction with respect to the actual LOS as follows. Let us assume LOS_i and ${\widehat{\mathit{LOS}}}_i$ (i = 1, …, n) are the true and predicted LOS value, respectively. We calculate the difference between ${\widehat{\mathit{LOS}}}_i$ and LOS_i as t_i. If t_i is smaller than a predefined tolerance threshold τ, we claim a correct prediction for the i^th patient:

$$b_i=\{\begin{array}{cc}1,& \left|{\widehat{\mathit{LOS}}}_i-{\mathit{LOS}}_i\right|\le \tau \\ 0,& \mathit{otherwise}\end{array}$$ (2)

The accuracy (Acc) of prediction is thus assessed as

$$\mathit{Acc}={\mathrm{\sum }}_{i=1}^n{b}_i/n$$ (3)

Experiment Design

This section begins with a description of four comparative models in our framework. We then describe how parameters are selected and compare the models on a range of values for the parameters. To calibrate the parameters and compare the models, we use 5 randomized runs of 3-fold cross-validation. Finally, we describe a hypothesis testing strategy to ascertain which features significantly influence the LOS prediction.

Models

Table 2 summarizes the four models. The baseline model M₀ uses age as a lone feature. The other three predictive models (M₁ to M₃) rely on one, two, and three-years worth of historical ICD-9 codes.

Table 2.

Comparative Models

Model	Description
M0	Age
M1	One year of ICD-9 codes
M2	Two years of ICD-9 codes
M3	Three years of ICD-9 codes

Parameter Selection

There are three parameters in the framework that need to be tuned: 1) number of trees in the random forest, 2) τ and 3) number of ICD-9 codes in the model. Since models M₁, M₂ and M₃ are the same in terms of the prediction algorithm, we leverage M₃ as a representative model to select an optimal value for each of the parameters.

Number of Trees

It has been shown that the performance of random forest regression is relatively insensitive to the number of trees [21]. However, selecting too small of a value can lead to poor accuracy, while too large of a value can lead to excessive computational load. Thus, we evaluated the models over a range for the nubmer of trees. We leveraged the distribution of predictive performance of the resulting random forest to select an optimal number. Specifically, we choose the value that maximizes accuracy and minimizes the number of trees.

LOS Threshold τ

The threshold τ introduced above represents the difference tolerance between the predicted LOS and the true LOS, but it will vary from one HCO to another. Thus, the accuracy in LOS prediction is evaluated under a set of thresholds {5, 12, 24, 36, 48}.

Number of Predictors

The number of ICD-9 codes (i.e., features) in this study is relatively large (i.e., 1849 in total). As such, we perform dimensionality reduction to derive a more manageable model. This is accomplished as follows. First, we sort the predictors on their importance in descending order. Second, we select a subset of the features and predict LOS. We choose the subset with the smallest size and highest accuracy.

Model Evaluation

There are three variables in our study and they are the number of trees, LOS threshold, and percent of predictors. Thus, three strategies are designed to evaluate our models in Table 3. In each strategy, two variables are held as constant while the third variable is varied.

Table 3.

Model evaluation strategies

Strategy	# Trees	τ	% Predictors
A	Vary	Constant	Constant
B	Constant	Vary	Constant
C	Constant	Constant	Vary

Feature Discrimination Analysis

A two-sample t-test is appled to compare LOS between patients with and without a certain ICD-9 code. We conduct this analysis for the ten ICD-9 codes with the highest importance, as derived from the random forest regression models. Specifically, for each investigated ICD-9 code, we test the significance of the LOS difference for patients with and without the code.

Results

Model Paramaterization

Figure 3 depicts the predictive performance of the models on a varying number of trees. The performance was evaluated while varing τ over 5, 12, 24, 36 and 48 hours. We selected 50 trees for our random forests because accuracy grows monotonically up to this point, after which it is constant.

Figure 3.

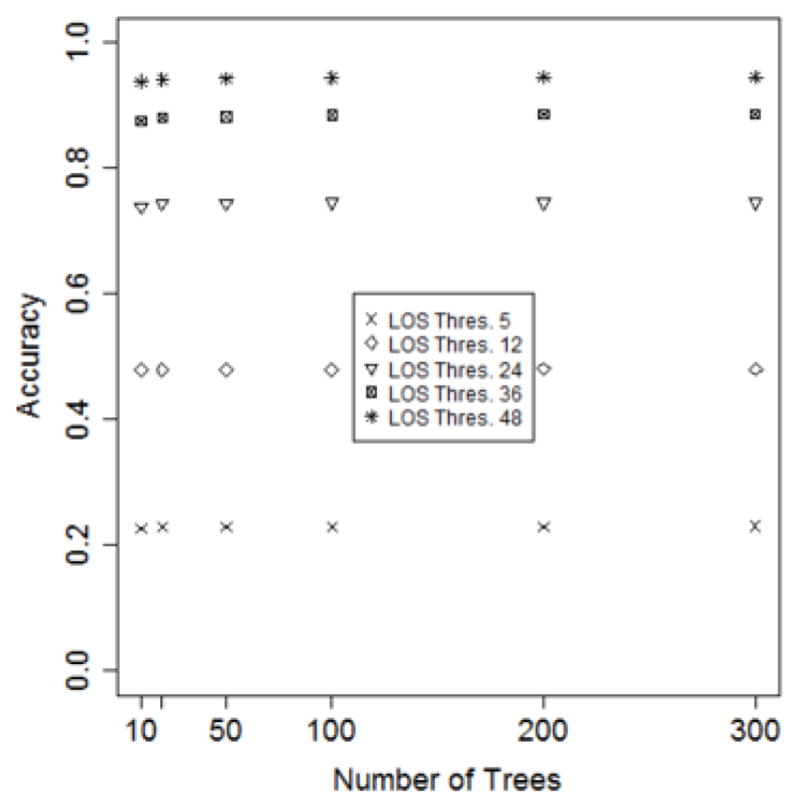
The accuracy of models as a function of the number of trees in the random forest.

The selection of τ depends on the requirements of an HCO. It can be seen in Figure 3 that the accuracy grows with τ. If an HCO can accept the predicted LOS between a range of 12 hours within the actual LOS, then 12 hours could be selected as the value of τ. Thus, for our investigation, we set τ to be 12 hours.

Our models are based on the top 10% of the features. This is based on the calibration shown in Figure 4, where it can be seen that model accuracy after this point remains relatively constant.

Figure 4.

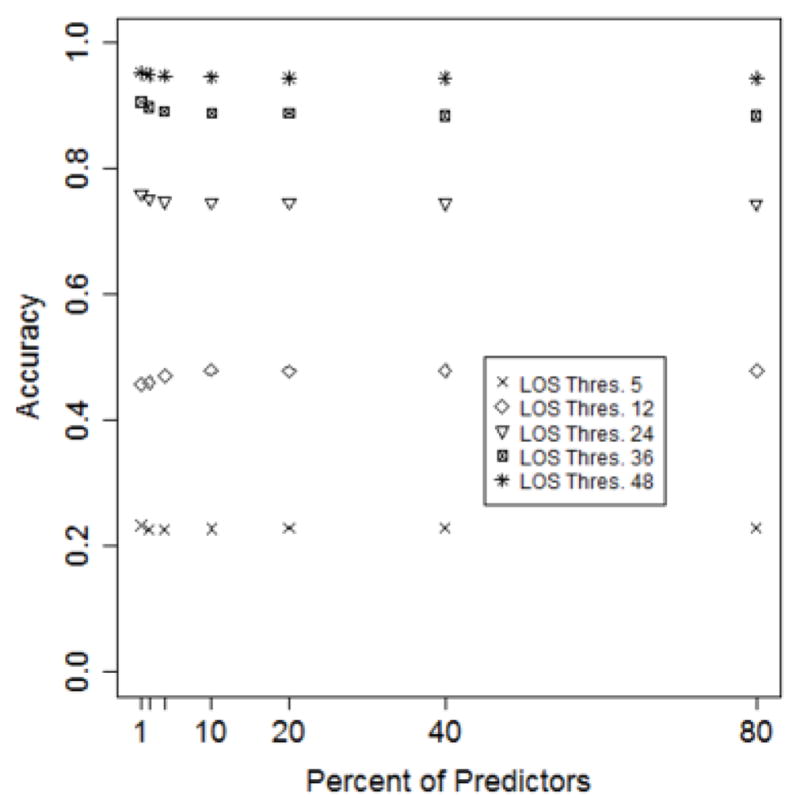
Model accuracy as a function of the number of features retained.

Model Evaluation

Figures 5–7 depict model performance as a function of the number of trees, LOS threshold and percent of features, respectively. In general, it can be seen that the models that incorporate ICD-9 codes have better performance than the baseline models. Additionally, models M₁, M₂ and M₃ have almost the same predictive performance. This suggests that one-year of historical ICD-9 codes may be sufficient for LOS prediction.

Figure 5.

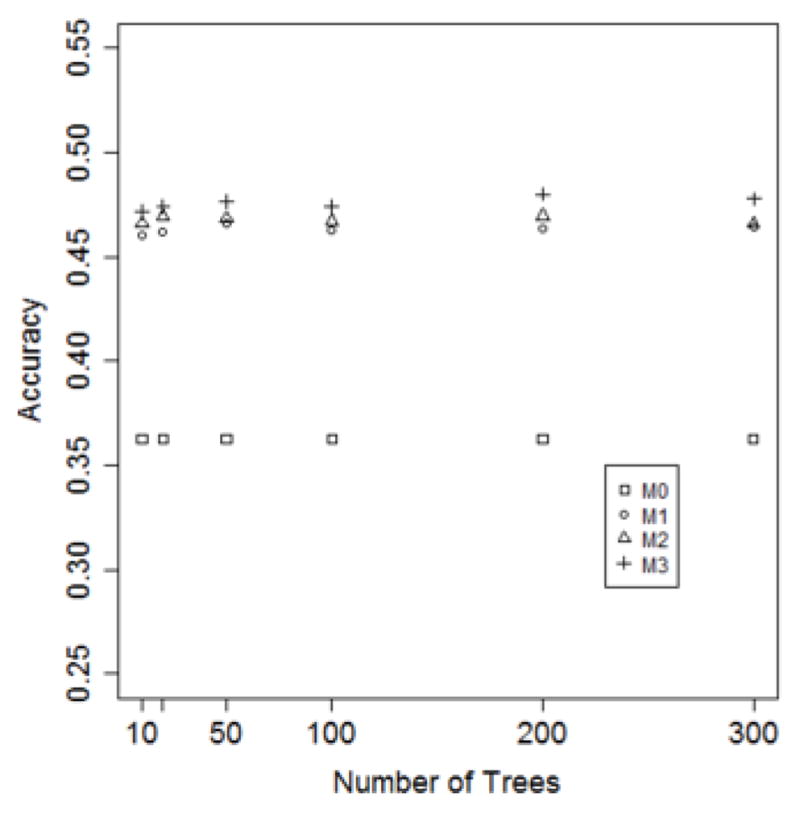
Model accuracy as a function of the number of decision trees. (τ = 12 hours; predictor set = top 10%)

Figure 7.

Model accuracy as a function of percent of predictors. (τ = 12 hours; Number of trees = 50).

The accuracy of the four models (where τ is set to 12 hours and the feature set is fixed to the top 10%) on a varying number of trees (10, 50, 100, 200 and 300) is shown in Figure 5. It can be seen that the accuracy of M₁, M₂ and M₃ is substantially higher than M₀. Additionally, the number of trees has minimal influence on the accuracy for all of the models.

In Figure 6, it can be seen that as the LOS threshold increases, all models improve in accuracy. However, the predictive performance does not improve when varying the percent of features, as is apparent in Figure 7.

Figure 6.

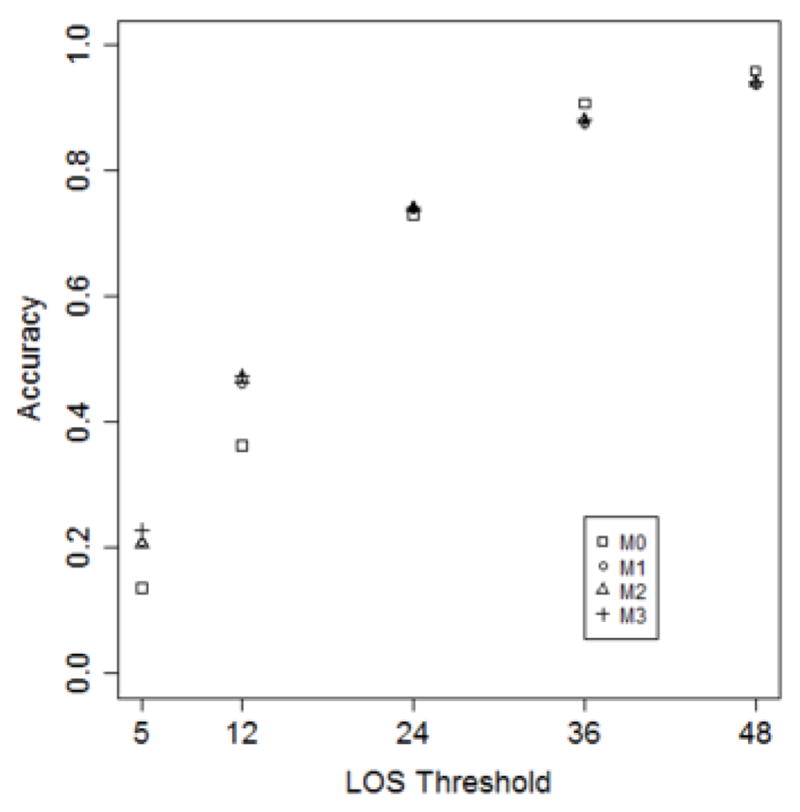
Model accuracy as a function of the LOS threshold. (Number of trees = 50; Predictor set = top 10%).

Finally, we conducted a series of experiments to predict LOS in two settings. In the first setting, we considered all patients whose LOS > 0. This was done to assees model performance on patients with a range of LOS. In the second setting, we restricted our analysis to the subset of patients whose LOS ≥ 96 hours. This allows us to study the model for predicting excessively long and costly LOS. To perform this analysis, we compare M₃ with its optimal parameterization (50 decision trees, 12 hours of LOS threshold, and top 10% features) with the baseline model. The results are shown in Table 4. It can be seen that M₃ (49.3%) outperforms M₀ (37.7%) with almost 30% improvement. Moreover, for patients with LOS ≥ 96 hours, M₃ (5.8%) outperforms M₀, which is incapable of predicting such excessively long stays.

Table 4.

Model comparison for all patients and patients with LOS ≥ 96

Model	Accuracy
	All patients (n = 7683)	LOS ≥ 96 hours (n = 1505)
M0	37.7%	0.00%
M3	49.3%	5.8%

Feature Discrimination Analysis

Out of 1849 ICD-9 codes, 10 were selected for further analysis in terms of their clinical implication (as shown in Table 5). Each of the codes in the top 10 ranks exhibited a statistically significant influence on the LOS between LOS for patients with and without such codes. Such evidence may help healthcare organizations (HCOs) to adopt resource allocation strategies that optimize the care management and improve care quality.

Table 5.

Summary for the top 10 most predictive ICD-9 codes

Importance Rank	ICD-9 code	Description	# of patients (with code vs. without code)	Mean LOS (with code vs. without code)	p-value
1	650	Normal delivery	2281 vs. 6907	58.1 vs. 76.5	<0.001
2	659.63	Elderly multigravida with antepartum condition or complication	1153 vs. 8035	81.0 vs. 70.6	<0.001
3	V28.81	Encounter for fetal anatomic survey	1899 vs. 7298	75.3 vs. 71.1	0.001
4	285.9	Unspecified anemia	343 vs. 8845	80.5 vs. 71.6	0.044
5	V28.89	Other specified antenatal screening	1580 vs. 7608	73.7 vs. 71.6	0.043
6	V28.4	Antenatal screening for fetal growth retardation using ultrasonics	384 vs. 8804	85.5 vs. 71.3	<0.001
7	V23.9	Unspecified high-risk pregnancy	531 vs. 8657	89.3 vs. 70.9	<0.001
8	V23.82	Supervision of high-risk pregnancy of elderly multigravida	137 vs. 9051	85.4 vs. 71.7	0.035
9	642.93	Unspecified hypertension antepartum	89 vs. 9099	109.8 vs. 71.6	<0.001
10	V76.2	Screening for malignant neoplasm of the cervix	582 vs. 8606	76.5 vs. 71.6	0.008

As an example, the most discriminant ICD-9 code was 650: “Normal Delivery”. The mean LOS for patients with and without Normal Delivery in their history was 58.1 and 76.5 hours, respectively. The p-value for this difference was less than 0.001. As another example, patients with ICD-9 code of 659.63 “Elderly multigravida with antepartum condition or complication” stayed about 10 more hours than those without that code (81 versus 70.6).

Discussion

The results show that the historical information in EMRs may assist in forecasting obstetric patients’ LOS in a hospital. Specially, our random forest regression model predicted LOS with an accuracy of 49% under an error range of 12 hours, which is 30% more accurate than a baseline model. The experimental results further demonstrate that a model based on the top 10% of ICD-9 codes can achieve an accuracy as high as those based on all involved ICD-9 codes (over 1800). Additionally, the models based on the most recent year of data logged in the EMRs can achieve similar performance to those based on two-, and three-year worth of data.

Notably, we also investigated the top 10 ICD-9 codes, which have significant differences in terms of LOS between patients with and without such codes. These results suggest that the HCOs can specialize resource allocation strategies accordingly.

Despite the merits of this investigation, we acknowledge that this is a pilot study and there are several limitations. First, the data was collected within a single institution and may not cover all of a patient’s medical history or be readily applicable to another hospital setting. Second, all of the patients in this study were on an obstetric service, such that the framework may not be directly extended to other types of patients or healthcare services. Third, the prediction of LOS may be considered lower than what one might want in a decision support system (i.e., an accuracy of 48% for ±12 hour). Other factors that potentially influence LOS can be incorporated in the model, such as certain patient demographics (e.g., race) or physical traits (e.g., height, weight or BMI).

Conclusions

This paper assessed the feasibility of a machine learningbased framework for predicting the length of stay for obstetric patients using historical diagnoses. We showed that one years worth of diagnostic history may be sufficient to predict hospitalization LOS with accuracy that is substantially higher than a baseline based solely on the age of the patient. We believe this research can be extended by including additional types of historical data (e.g., medications) and leveraging the chronological order of such knowledge.