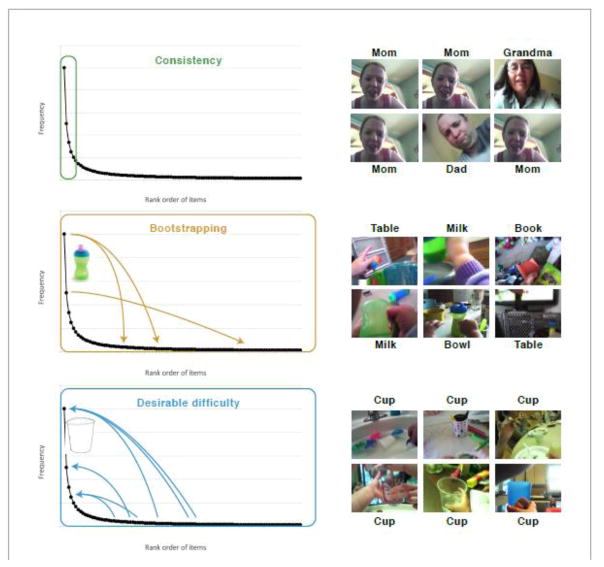
Fig. 3. Three hypotheses about how heavy-tailed distributions may support learning.

Theoretical frequency distributions are plotted such that the frequency of an object in visual scenes is plotted as function of the rank order of frequency of all objects. How might learners make use of the data with this distributional structure? One possibility, the Consistency hypothesis, is that they learn only about the high frequency items, for example only about the high frequency faces and that learning is relatively unaffected by the properties of other more rarely encountered faces. A second possibility, the Bootstrapping hypothesis, is that learners learn about both the high frequency and low frequency and low frequency objects and that learning about the high frequency objects supports learning about the other rarer objects. For example, the learner may be better able to visually find a low frequency object in clutter (e.g., the book) if it in a context with high frequency visual objects. The third hypothesis, Desirable Difficulties, is that learners may learn most robustly about the high frequency objects but that learning is helped by encountering the high-frequency objects (the cup) in many different scenes with many other different objects.