Role of Ligand-Driven Conformational Changes in Enzyme Catalysis: Modeling the Reactivity of the Catalytic Cage of Triosephosphate Isomerase

Abstract

We have previously performed empirical valence bond calculations of the kinetic activation barriers, ΔG^‡_calc, for the deprotonation of complexes between TIM and the whole substrate glyceraldehyde-3-phosphate (GAP, Kulkarni et al. J. Am. Chem. Soc. 2017, 139, 10514–10525). We now extend this work to also study the deprotonation of the substrate pieces glycolaldehyde (GA) and GA·HP_i [HP_i = phosphite dianion]. Our combined calculations provide activation barriers, ΔG^‡_calc, for the TIM-catalyzed deprotonation of GAP (12.9 ± 0.8 kcal·mol^–1), of the substrate piece GA (15.0 ± 2.4 kcal·mol^–1), and of the pieces GA·HP_i (15.5 ± 3.5 kcal·mol^–1). The effect of bound dianion on ΔG^‡_calc is small (≤2.6 kcal·mol^–1), in comparison to the much larger 12.0 and 5.8 kcal·mol^–1 intrinsic phosphodianion and phosphite dianion binding energy utilized to stabilize the transition states for TIM-catalyzed deprotonation of GAP and GA·HP_i, respectively. This shows that the dianion binding energy is essentially fully expressed at our protein model for the Michaelis complex, where it is utilized to drive an activating change in enzyme conformation. The results represent an example of the synergistic use of results from experiments and calculations to advance our understanding of enzymatic reaction mechanisms.

Triosephosphate isomerase (TIM), orotidine 5′-monophosphate decarboxylase (OMPDC), and glycerol 3-phosphate dehydrogenase (GPDH) utilize protein binding interactions with their substrate dianions to drive conformational changes from floppy, inactive, open enzymes to structured, catalytically active cages for the substrate.¹ This dianion activation provides the high specificity in transition state binding that is one hallmark of efficient enzymatic catalysis.^1c The development of an understanding of the mechanism for dianion activation is tightly linked to the broader issue of allosteric activation of enzyme catalysis,² and the mechanism by which enzymes achieve their high specificity in transition state binding. The latter has been a goal of mechanistic enzymologists since Jencks first described the complexity of this problem in a classic 1975 review.³

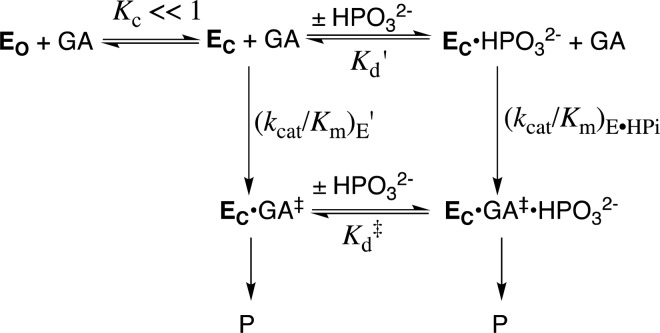
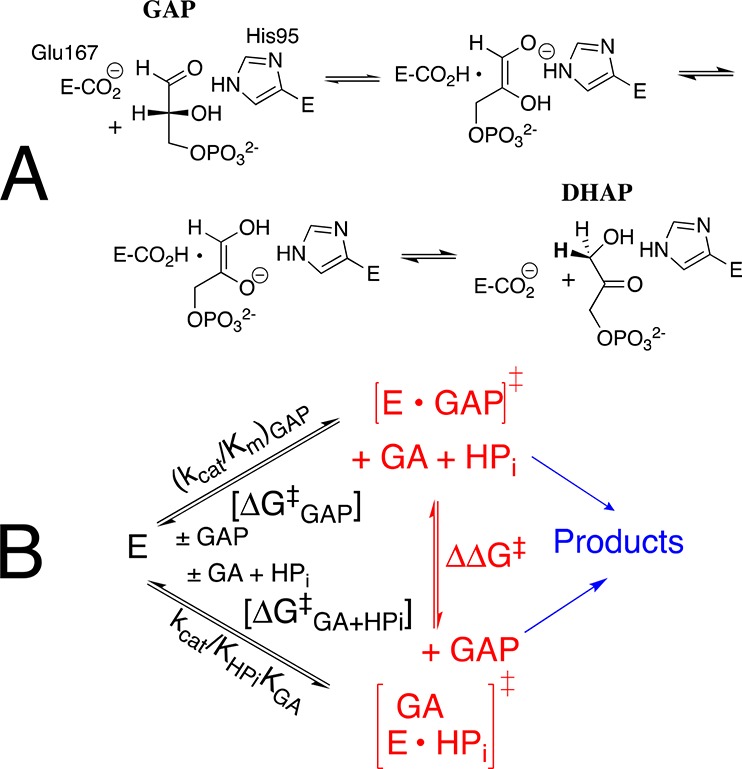
TIM catalyzes the conversion of dihydroxyacetone phosphate (DHAP) to (R)-glyceraldehyde 3-phosphate (GAP), through enzyme-bound cis-enediolate reaction intermediates (Scheme 1A),⁴ and phosphite dianion-activated deprotonation of glycolaldehyde (GA).⁵ The kinetic parameters, k_cat/K_m (M^–1 s^–1), for the TIM-catalyzed isomerization of the whole substrate GAP to form DHAP, and k_cat/K_GAK_HPi (M^–2 s^–1) for phosphite dianion activated reactions of the substrate piece GA (Scheme 1B), determined for 14 different wild-type and site-directed mutant forms of TIM, define an extraordinary linear free energy relationship (LFER), with slope of 1.0, between the activation barriers ΔG^‡ for the wild-type and mutant enzyme-catalyzed reactions of the whole substrate and substrate pieces.⁶ The LFER is consistent with Scheme 2,^6a which shows dianion activators as functioning exclusively to stabilize the active closed form of TIM (E_C).^1c,5a This closed form exists at low concentrations in the absence of the activating dianion (K_c ≪ 1): the dianion binding interactions are utilized to mold the inactive open enzyme (E_O) into the structured and fully active catalyst,^1a,1b as described originally in Koshland’s induced fit model.⁷ Once these binding interactions are expressed at E_C, the dianion becomes a spectator that does not affect the reactivity of the truncated carbon acid GA [(k_cat/K_m)_E′ = (k_cat/K_m)_E•HPi, Scheme 2].

Scheme 1. (A) Mechanism for the TIM-Catalyzed Reaction; (B) TIM-Catalyzed Reactions of GAP and the Substrate Pieces GA·HP_i.

Scheme 2. Model for the TIM-Catalyzed Reaction of the Substrate Pieces that Separates the Enzyme Conformational Change (K_c) from Deprotonation of Bound Substrate.

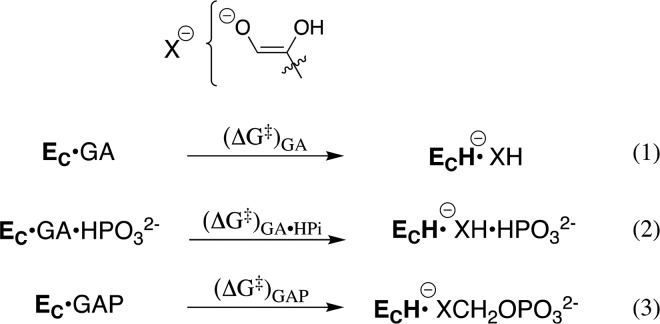
Scheme 2 separates the conformational change of TIM from the chemical reaction catalyzed by E_C, and shows a significant thermodynamic barrier to this conformational change in the absence of ligand (K_c ≪ 1, Scheme 2). The energetic price to formation of E_C is paid for by utilization of binding interactions with nonreacting substrate fragments (e.g., phosphodianions).^1a These binding interactions are assumed to be fully expressed at E_C, and therefore cannot act to reduce the activation barrier, ΔG^‡, for TIM-catalyzed proton transfer from the carbon acid to the carboxylate side chain of E165. This assumption predicts similar activation barriers for the proton transfer reactions shown in Scheme 3. This surprising prediction cannot be tested by experiment, because the weak observed binding interactions between TIM and the substrate pieces precludes saturation of E_C by the pieces GA·HP_i.⁸ The prediction can, however, be examined by reliable computational methods, and provides a novel opportunity for synergistic use of results from experiments and calculations to advance our understanding of enzyme catalysis.

Scheme 3. Proton Transfer from TIM-Bound Carbon Acids to the Carboxylate Side Chain of E165.

TIM has been the subject of substantial computational work, using a range of computational approaches,⁹ including empirical valence bond (EVB) simulations.^9c,10 We recently reported results of EVB calculations of the kinetic and thermodynamic barriers, ΔG^‡ and ΔG⁰, for proton transfer to the carboxylate side chain of E165 at the E_C·DHAP and E_C·GAP complexes of wild-type TIM, to form enediolate reaction intermediates (Scheme 3, eq 3), as well as the activation barriers for these proton transfers catalyzed by I170A, L230A and I170A/L230A mutant forms of TIM.^10c These calculations used the 1.2 Å resolution X-ray crystal structure for TIM in complex with DHAP (PDB ID: 1NEY) to model the structure of TIM bound to other ligands. The excellent agreement between the experimental and calculated activation barriers validates these computational protocols for use in modeling of similar TIM-catalyzed reactions.

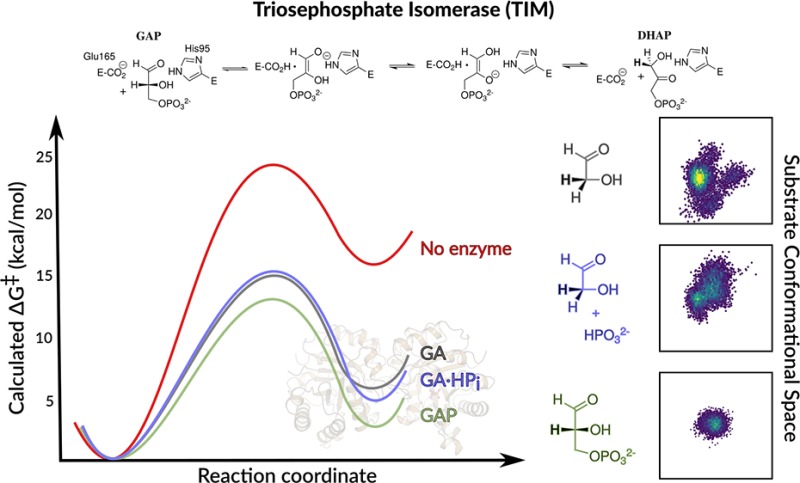
The EVB simulations presented here for the reactions in eqs 1 and 2 for Scheme 3 were performed using the methodology described in the Supporting Information, which is similar to the previous protocol used to model the activation barriers for deprotonation of GAP (Scheme 3, eq 3).^10c GA may bind to E_C with the substrate carbonyl either adjacent to [DHAP conformation], or distant [GAP conformation] from the dianion binding site (Figure S1). The determination of the fractional contribution of these two conformations to the overall reactions of [1-¹³C]-GA in D₂O is problematic.^5a The activation and reaction free energies for the TIM-catalyzed deprotonation of complexes to GA and GA·HP_i (GAP conformation) to form the respective enediolate reaction intermediates, and previously published activation barriers for the deprotonation of GAP in water and at TIM,^10c are reported in Table 1, and the geometric parameters in Tables S1 and S2. The computational results give a ∼1.5 kcal·mol^–1 smaller barrier for deprotonation of GA in the GAP conformation [Supporting Information], and our analysis will therefore focus on this more reactive GAP conformation. Table 1 shows that the range of values for ΔG^‡_calc (2.6 kcal·mol^–1) and ΔG⁰_calc (3.5 kcal·mol^–1) for the TIM-catalyzed deprotonation of the Michaelis complex to the whole substrate GAP, and of the Michaelis complex to GA or to GA·HP_i are within the uncertainty of the computed values for the reactions of the substrate pieces, but small in comparison to the calculated effect of the enzyme catalyst on ΔG^‡_calc (11.2 kcal·mol^–1) and ΔG⁰_calc (13.6 kcal·mol^–1). These results show that dianions behave as spectators at the Michaelis complex, and do not affect the stability of the transition state for TIM-catalyzed proton transfer.^6b

Table 1. Barriers for Nonenzymatic Deprotonation of GAP, and for the TIM-Catalyzed Deprotonation of GAP, GA, and GA·HP_i, at 25 °C^a.

Substrate	kcat (s–1)b	kcat/KM (M–1 s–1)b	ΔG‡exp (kcal·mol–1)c	ΔG‡calc (kcal·mol–1)c	ΔG0calc (kcal·mol–1)c
CH3CH2CO2–+ GAPd	N.A.	N.A.	24.0	24.1 ± 0.2	16.1 ± 0.2
GA	N.A.	0.07	N.A.	15.0 ± 2.4	6.0 ± 2.8
GA·HPi	N.A.	64	N.A.	15.5 ± 3.5	4.8 ± 4.2
GAP	2100	8.4 × 106	12.9	12.9 ± 0.8	2.5 ± 0.9

^aN.A., not available.

^bKinetic parameters from ref (11).

^cThe calculated activation or reaction free energies were obtained as averages and standard deviations over 30 independent EVB trajectories, as described in the Supporting Information. The standard error of the mean (s.e.m.) is ≤0.8 kcal·mol^–1 and <0.2 kcal·mol^–1 for the reactions of the pieces, and whole substrate, respectively. The experimental activation free energies, ΔG^‡_exp, were obtained from k_cat using transition state theory.

^dActivation barriers for the nonenzymatic reaction from refs (10c, 11).

The electrostatic contributions of the different amino acid side chains to the calculated activation free energies were extracted from the corresponding EVB trajectories using the linear response approximation¹² (Figure 1 and Table S3), using a dielectric constant of 4 to describe the protein environment, as in our previous work.^10cFigure 1 shows that these interactions are likewise similar for the TIM-catalyzed reactions of the whole substrate GAP and for the substrate in pieces. For example, the interaction with the cationic side chain of K12 is only ca. 1.0 kcal·mol^–1 stronger at the transition state for the TIM-catalyzed deprotonation of GAP compared with GA.

Figure 1.

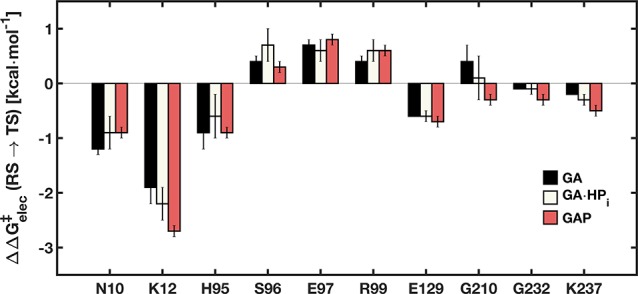
Electrostatic contributions (ΔΔG^‡_elec ≥ 0.1 kcal·mol^–1) of individual amino acid side chains to the calculated activation free energies for the deprotonation of the substrate pieces GA and GA·HP_i, as well as the full substrate GAP. The error bars represent the standard deviation of each value over 30 independent EVB trajectories.

We are uncertain of the significance of the small variations in ΔG^‡_calc and ΔG⁰_calc (Table 1). A higher entropic barrier to deprotonation of the loose complex to GA, compared to the tighter complexes to GAP or GA·HP_i will be observed if this results in a larger change in the conformational flexibility of the protein on proceeding to the “tight” transition states for the proton transfer reactions. This proposal is supported by Figure 2, which shows a comparison of the conformational space sampled by the substrate pieces GA, GA·HP_i and by the full substrate GAP at the Michaelis complex (Figure 2A–C) and at the transition state for proton transfer to the enzyme (Figure 2D–F). The relatively large contraction in the conformational space sampled by the complex to GA on proceeding from the Michaelis complex (Figure 2A,B) to the transition state complex (Figure 2D,E), is consistent with a significant entropic barrier to the restriction of protein and ligand motions. By comparison, the conformational space sampled by the Michaelis complex to GAP is already restricted by protein–dianion interactions (Figure 2C), and shows only slight changes at the transition state for proton transfer (Figure 2F).

Figure 2.

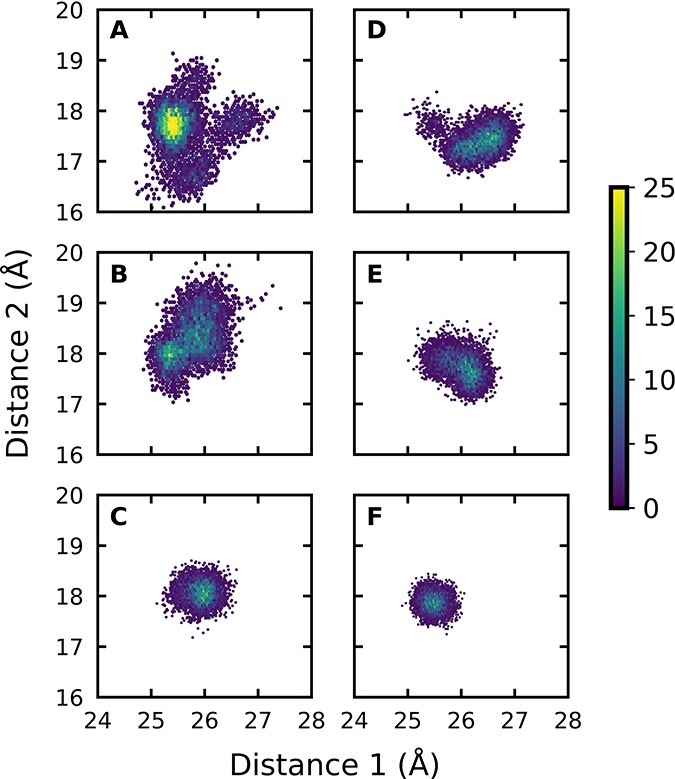
Conformational space sampled by GA and GA·HP_i, as well as GAP (shown by population densities), at the Michaelis complexes (A–C) and transition states (D–F). The x- and y-axes give the distances between the donor carbon atoms of the substrate and the backbone α-amino acid carbon atoms of D111 in Chain B and I19 in Chain A, respectively. The full details of this analysis are provided in the Supporting Information.

We note here that the precision (standard deviation, Table 1) of the calculations does not provide a measure of accuracy. On the basis of our prior calculations of the TIM-catalyzed deprotonation of the full substrates DHAP and GAP by wild-type and mutant TIM,^10c we estimate an accuracy of ±1.0 kcal·mol^–1 for the calculated activation free energies, as that was the level of agreement with experimental data obtained using our model. In addition, the variations in ΔG^‡_calc and ΔG⁰_calc (Table 1) are small in comparison to the 12.0 and the 5.8 kcal·mol^–1 intrinsic phosphate and intrinsic phosphite dianion binding energy utilized in the stabilization of the transition states for the TIM-catalyzed isomerization of GAP,¹³ and for the deprotonation of GA,¹⁴ respectively. We conclude that these intrinsic dianion binding energies are essentially fully utilized [expressed] at the complexes between GAP or GA and E_C; and that E_C shows the full reactivity toward the deprotonation of bound GAP or GA·HP_i. The complexes to the substrate GAP or to the pieces GA·HP_i are stabilized by interactions between TIM and the bound dianion. The activated complex to GA is conformationally unstable compared with free enzyme,^1a,5a but has a reactivity for deprotonation of the bound carbon acid that is similar to that for complexes to GA·HP_i or GAP (Table 1).

Calculations to model the barrier for moving from the Michaelis complex to the transition state for the catalyzed reaction are implicitly assumed to encompass the most important features of enzymatic catalysis. This focus on the Michaelis complex neglects to consider the mechanism for the utilization of the large intrinsic binding energy of nonreacting substrate fragments in transition state stabilization,³ which gives rise to dianion activation of the reaction of the truncated substrate piece.^1a The present computational studies strongly suggest that the total intrinsic dianion binding energy is essentially entirely expressed at the Michaelis complex to the substrate pieces (Table 1). This provides strong support for the conclusion that the difference between the intrinsic and the observed dianion binding energy is equal to the binding energy utilized to drive an uphill enzyme conformational change during formation of the Michaelis complex (Scheme 2).¹ We are working on developing computational protocols to formally calculate the dianion binding energy that is utilized to drive the conformational change of TIM.

These calculations may be generalized to other enzymatic reactions, where the binding energy of a nonreactive substrate fragment, such as a phosphodianion,^1c coenzyme A,¹⁵ or an NAD cofactor,¹⁶ is utilized to stabilize a catalytically active enzyme conformation. Briefly, when a fragment functions to stabilize an active enzyme conformation, then the function is fulfilled upon formation of the complex, so that removal of the fragment is then predicted to have no effect on the activation barrier for the subsequent conversion of this complex to the rate-determining transition state (Table 1).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b00251.

• Computational methodology, additional simulation details, and the empirical valence bond parameters used to describe the deprotonation of GA and GA·HP_i (PDF)

The authors declare no competing financial interest.