Identification of associations between genotypes and longitudinal phenotypes via temporally-constrained group sparse canonical correlation analysis

Abstract

Motivation

Neuroimaging genetics identifies the relationships between genetic variants (i.e., the single nucleotide polymorphisms) and brain imaging data to reveal the associations from genotypes to phenotypes. So far, most existing machine-learning approaches are widely used to detect the effective associations between genetic variants and brain imaging data at one time-point. However, those associations are based on static phenotypes and ignore the temporal dynamics of the phenotypical changes. The phenotypes across multiple time-points may exhibit temporal patterns that can be used to facilitate the understanding of the degenerative process. In this article, we propose a novel temporally constrained group sparse canonical correlation analysis (TGSCCA) framework to identify genetic associations with longitudinal phenotypic markers.

Results

The proposed TGSCCA method is able to capture the temporal changes in brain from longitudinal phenotypes by incorporating the fused penalty, which requires that the differences between two consecutive canonical weight vectors from adjacent time-points should be small. A new efficient optimization algorithm is designed to solve the objective function. Furthermore, we demonstrate the effectiveness of our algorithm on both synthetic and real data (i.e., the Alzheimer’s Disease Neuroimaging Initiative cohort, including progressive mild cognitive impairment, stable MCI and Normal Control participants). In comparison with conventional SCCA, our proposed method can achieve strong associations and discover phenotypic biomarkers across multiple time-points to guide disease-progressive interpretation.

Availability and implementation

The Matlab code is available at https://sourceforge.net/projects/ibrain-cn/files/.

1 Introduction

Integrating neuroimaging and molecular genetics technology hold great promising to use brain imaging as quantitative phenotypes to investigate the role of genetic variations. These imaging quantitative traits (QTs) serve as intermediate phenotypes with rich information, which bridge the gap between genetic factors and phenotypic outcomes (Glahn et al., 2007; Gottesman and Gould, 2003; Hariri et al., 2006) and may lead to a better understanding of the complex biological mechanism underlying neurodegenerative diseases [e.g., mild cognitive impairment (MCI), the prodromal stage of Alzheimer’s disease (AD)].

In prior imaging genetic studies, pairwise univariate analysis strategies have been performed to identify the associations between single nucleotide polymorphisms (SNPs) and neuroimaging QTs. The most comprehensive studies focused on scanning the entire brain and the entire genome (Shen, et al., 2010; Stein et al., 2010). In recent studies, taking into account the inherent structure among genotype or phenotype data, some researchers have developed generalized multivariate linear regression models (Hibar et al., 2011; Kohannim et al., 2011, 2012; Vounou et al., 2010; Wang et al., 2012a) and structured bi-multivariate models (Chi et al., 2013; Lin et al., 2014; Yan et al., 2014) to identify multi-SNP-multi-QT associations. Those methods have sufficient power to discover structured phenotypic imaging markers associated with disease-relevant SNPs. However, examining genetic influence on the longitudinal profiles of imaging phenotype is still an under-explored topic in imaging genetics. Specifically, a straight forward approach such as conventional sparse canonical correlation analysis (SCCA) (Chi et al., 2013; Witten et al., 2009; Witten and Tibshirani, 2009), which does not take into account the valuable information conveyed by the longitudinal pattern of phenotypic input, is to perform multi-SNP-multi-QT associations at one time-point. In fact, the phenotypes across multiple time-points may exhibit temporal patterns that can be used to describe the degenerative process. Some studies have investigated on prediction of memory impairment and cognitive assessments with longitudinal magnetic resonance imaging (MRI) data (Jie et al., 2016; Wang et al., 2016).

So far, only a few machine-learning strategies have been proposed to examine how the phenotypic changes are that affected by SNPs. Recently, Wang et al. (2012b) proposed a novel task-correlated longitudinal sparse regression model to study the association between phenotypic imaging markers and the genotypes by taking into account the temporal structure of the longitudinal imaging data. More specifically, they used L21-norm for regression coefficient matrix to jointly select imaging markers that have common effects across all time-points. However, the task-correlated longitudinal sparse regression model assumed that longitudinal imaging markers were related to all candidate SNPs as a task-correlated constraint, which might not hold in real applications. More recently, Vounou et al. (2010) have proposed a two-step framework based on sparse reduced-rank regression to solve the imaging genetics problem for the genome-wide detection of markers associated with voxel-wise longitudinal changes in brain (Vounou et al., 2012). They first pre-selected the disease relevant voxel level imaging phenotypes with high-classification performance between AD and NC group by penalized linear discriminant analysis, and then identified the SNPs associated with the multivariate imaging phenotypes from the first step. This approach might be inadequate to capture the dynamics of phenotypic trajectories and thus unable to detect the underlying temporal patterns. Therefore, how to identify the longitudinal phenotypes across consecutive time-points associated to the disease sensitive SNPs is still an important topic in imaging genetic studies.

With these observations, the motivation of this study is to identify associations between risk genotypes and longitudinal phenotypes, where we aim to design a powerful model to simultaneously maximize progression-relevant imaging genetic associations and capture the consecutive changes in brain between adjacent time-points. Accordingly, as shown in Figure 1, we propose a novel temporally constrained group sparse canonical correlation analysis (TGSCCA) framework that incorporates the group sparsity constraint and fused penalty to identify the associations between genetic factors and longitudinal phenotypes. In particular, it is promising to find the consecutive patterns that are robust to noises or outliers via considering both joint selection and the fused information in imaging phenotypes from adjacent time-points.

Fig. 1.

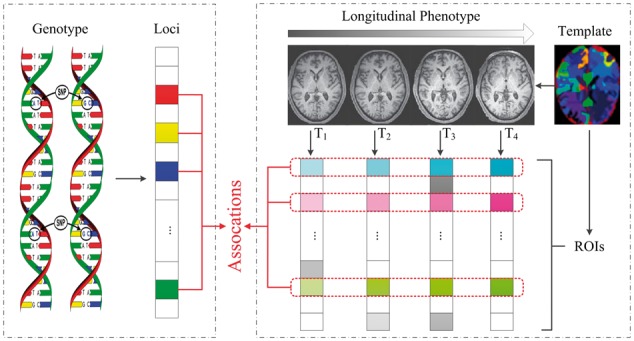
Schematic illustration of TGSCCA for imaging genetics

In this study, to evaluate the effectiveness and efficiency of our proposed method, we perform experiments on both synthetic and real data. For real data, using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) cohort (Mueller et al., 2005), we examine imaging genetic associations between SNPs nearby the apolipoprotein E (APOE) gene and region of interest (ROI) measures extracted from longitudinal structural MRI. The empirical results show that our method not only yields clearly improved association performance under the metrics of correlation coefficient but also detects relevant risk SNP loci and imaging ROI markers.

The rest of this article is organized as follows. Section 2 introduces the TGSCCA method. The performances of the proposed method are evaluated through both simulations and real data analysis in Section 3. The last section concludes the study.

2 Materials and methods

2.1 Sparse Canonical Correlation Analysis (SCCA)

We first describe relevant notations to present imaging genetic association analysis. We use lowercase letters to denote vectors, and uppercase letters to denote the matrices. Let $X={[x_1,\dots ,x_n,\dots ,x_N]}^{\mathrm{T}}\in R^{N\times p}$ be the SNP genotype data, ${[y_1,\dots ,y_n,\dots ,y_N]}^{\mathrm{T}}\in R^{N\times q}$ be the phenotype data, where N is the number of participants, and p and q are the feature number of SNPs and imaging data, respectively.

Canonical correlation analysis (CCA) is a powerful association method that seeks linear transformations of two data sets $X$ and $Y$ to achieve the maximal correlation between $Xu$ and $Yv$ (Hotelling, 1935), which can be formulated as:

$$\underset{w,v}{\max }{u}^{\mathrm{T}}{X}^{\mathrm{T}}Yv$$

$$s.t.\mathrm{ }{u}^{\mathrm{T}}{X}^{\mathrm{T}}Xu=1,\mathrm{ }{v}^{\mathrm{T}}{Y}^{\mathrm{T}}Yv=1,$$ (1)

where we assume that the columns of $X$ and $Y$ are standardized to have zero mean and unit variance, and $u$ and $v$ are canonical weights, reflecting the contribution of each feature in the identified canonical correlation. However, in imaging genetics applications, the traditional CCA model tends to overfit and does not yield desirable results as the dimension of the data is much higher than the sample size. In addition, the CCA outcome could spread nontrivial effects across all features, which are not desirable for applications needing to identify relevant features. To address these issues, sparse version of CCA (SCCA) (Chi et al., 2013; Witten et al., 2009; Witten and Tibshirani, 2009) has been proposed by introducing penalties with L1 regularization for variable selection (Tibshirani, 2011) as follows:

$$\underset{w,v}{\max }{u}^{\mathrm{T}}{X}^{\mathrm{T}}Yv$$

$$s.t.\mathrm{ }{\left|\right|Xu\left|\right|}_2^2=1,\mathrm{ }{\left|\right|Yv\left|\right|}_2^2=1,\mathrm{ }{\left|\left|u\right|\right|}_1\le c_1,{\left|\left|v\right|\right|}_1\le c_2$$ (2)

where the constraints ${\left|\left|u\right|\right|}_1\le c_1$ and ${\left|\left|v\right|\right|}_1\le c_2$ are regularization term for the objective function, and $c_1$ and $c_2$ is the corresponding regularization parameters. In imaging genetics applications, the weight vectors $u$ and $v$ measure the relative contributions of the SNP loci and imaging phenotype ROIs. For easy computation, the variance matrix of $X$ and $Y$ is treated as diagonal matrix, which has shown to be effective and efficient for high-dimensional data (Grellmann et al., 2015; Witten et al., 2009).

2.2 Temporally constrained group sparse canonical correlation analysis (TGSCCA)

In clinical practice, imaging phenotypes affected by genetic factors changes over time. To investigate the association between genotypes and longitudinal imaging phenotypes, in this article, we consider how to perform bi-multivariate association analysis across the consecutive time-points. Assume that we have $N$ training subjects, and each subject has imaging data derived from $T$ different time-points. Given the genotype SNPs data $X={[x_1,\dots ,x_n,\dots ,x_N]}^{\mathrm{T}}\in R^{N\times p}$and longitudinal imaging phenotypes$\mathrm{ }{Y}_t={[y_{1t},\dots ,y_{nt},\dots ,y_{Nt}]}^{\mathrm{T}}\in R^{N\times q}$ at time-point $t$ ($1\le t\le T$) as input in the association model, where $N$ is the number of participants, $p$ and $q$ are the numbers of feature dimensionalities (i.e., number of SNP loci and brain imaging ROIs). As described in Section 1 and Figure 1, our aim is to discover those longitudinal brain imaging markers associated with genetic factors across different time-points. Task-correlated longitudinal analysis model has recently been successfully investigated and applied to regression problems (Wang et al., 2012a, b), which are inspired by using multi-task learning framework (Liu et al., 2009; Obozinski et al., 2006) in machine-learning community. Following their previous work, we induce the joint penalty term L21-norm into the Equation (2) and then develop group sparse canonical correlation analysis (GSCCA) model as follows:

$$\underset{u,V}{\min }-\sum _{t=1}^T{u}^{\mathrm{T}}{X}^{\mathrm{T}}{Y}_t{v}_t+{\lambda }_u{\left|\left|u\right|\right|}_1+{\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}$$

$$s.t.\mathrm{ }{\left|\right|Xu\left|\right|}_2^2=1,\mathrm{ }{\left|\right|Y_t{v}_t\left|\right|}_2^2=1$$ (3)

where the weight vector $u$ and $v_t$ measure the relative importance of the SNP loci and imaging phenotype ROIs at time-point $t$ ($1\le t\le T$). ${\lambda }_u$ and ${\lambda }_v$ denote control parameters of the regularization terms, respectively. $V=[{v_1,\dots ,v}_t,\dots ,v_T]\in R^{q\times T}$ is the weight matrix whose row $v_i$ is the vector of coefficients assigned to the -th feature across different time-points, and ${\left|\left|V\right|\right|}_{\mathrm{2,1}}={\sum }_{i=1}^d{\left|\right|V^i\left|\right|}_2$ is to penalize all coefficients in the same row of matrix $V$ for joint feature selection. It is worth noting that the L21 regularization term can be coupled over time dimension and this “group-sparsity” regularizer forces only a small number of features being selected (Yuan and Lin, 2006). In other words, the longitudinal imaging features across all time-points will be identified.

To further take into account detecting temporally-constrained imaging genetic associations, we expect to develop our model to explore the association between baseline SNPs and longitudinal imaging phenotypes for a better understanding of underlying progressive mechanism specific to the disease. More specifically, motivated by the existing work (Jie et al., 2016), we induce a new regularization term called fused least absolute shrinkage and selection operator (Lasso) (Liu et al., 2010) in machine-learning community and then formulate the TGSCCA model as follows:

$$\underset{u,V}{\min }-\sum _{t=1}^T{u}^{\mathrm{T}}{X}^{\mathrm{T}}{Y}_t{v}_t+{\lambda }_u{\left|\left|u\right|\right|}_1+{\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}+{\lambda }_t\sum _{t=1}^{T-1}{\left|\left|v_{t+1}-v_t\right|\right|}_1$$

$$s.t.\mathrm{ }{\left|\right|Xu\left|\right|}_2^2=1,\mathrm{ }{\left|\right|Y_t{v}_t\left|\right|}_2^2=1$$ (4)

where the weight vectors $u$ and $v_t$ measure the relative contributions of the SNP loci and imaging phenotype ROIs at time-point $t$. The weight vector $v_{t+1}$ and $v_t$ are from adjacent time-points. ${\lambda }_u$, ${\lambda }_v$ and ${\lambda }_t$ denote control parameters of the regularization terms, respectively. The fused Lasso regularization term tends to constrain the differences between two successive canonical weight vectors from adjacent time-points to be small, that is the smoothness of weight vectors encourages neighboring features to be selected together. Due to the two regularization terms in Equation (3), it is promising to find the better solution that is robust to noises or outliers via considering both joint selections and the fused information inherent in imaging genetic associations.

2.3 Optimization algorithm

In this section, we introduce the algorithm to obtain $u$ and $V$ from Equation (4). The objective function is convex with respect to $u$ when $V$ is fixed and vice versa. So the iteration procedures mainly contain two steps as follows:

$$\underset{u}{\min }-\sum _{t=1}^T{u}^{\mathrm{T}}{X}^{\mathrm{T}}{Y}_t{v}_t+{\lambda }_u{\left|\left|u\right|\right|}_1$$

$$s.t.\mathrm{ }{\left|\right|Xu\left|\right|}_2^2=1$$ (5)

$$\underset{V}{\min }-\sum _{t=1}^T{u}^{\mathrm{T}}{X}^{\mathrm{T}}{Y}_t{v}_t+{\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}+{\lambda }_t\sum _{t=1}^{T-1}{\left|\left|v_{t+1}-v_t\right|\right|}_1$$

$$s.t.\mathrm{ }{\left|\right|Y_t{v}_t\left|\right|}_2^2=1$$ (6)

We can use the Lagrange multiplier and write the penalties into the matrix form for Equation (5), thus the new objective function is as follows:

$$\underset{u}{\min }-\sum _{t=1}^T{u}^{\mathrm{T}}{X}^{\mathrm{T}}{Y}_t{v}_t+{\lambda }_u{\left|\left|u\right|\right|}_1+{\frac{\theta }{2}\left|\right|Xu\left|\right|}_2^2$$ (7)

where ${\lambda }_u$ and $\theta$ are the model parameters. In this solution, a smooth approximation has been estimated for L1 term by including an extremely small value. Take the derivative regarding ${\lambda }_u$ and let it be 0. The solution for $u$ in each iteration step is as follows:

$$u={\left(X^{\mathrm{T}}X+\frac{{\lambda }_u}{\theta }D\right)}^{-1}\left(\sum _{t=1}^T{X}^{\mathrm{T}}{Y}_t{v}_t\right)$$ (8)

where $D$ is a diagonal matrix with the $k$th element as $1/2{\left|\right|u^k\left|\right|}_1\mathrm{ }(k\in [1,p\left]\right)$.

To obtain $V$ when $u$ is fixed for Equation (6), we follow the previous work (Fang et al., 2016; Witten et al., 2009) and assume that the variance matrix of $Y_t$ is treated as diagonal matrix, which has shown to be effective and efficient for optimization. The solution for $V$ in each iteration step is as follows:

$$\underset{{\left|\right|v_t\left|\right|}_2^2=1}{\min }\sum _{t=1}^T{{-z}_t}^{\mathrm{T}}{v}_t+{\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}+{\lambda }_t\sum _{t=1}^{T-1}{\left|\left|v_{t+1}-v_t\right|\right|}_1$$ (9)

where $z_t=Y_t^{T}Xu$, is given by ${\left|\right|v_t\left|\right|}_2^2=1$, where $V$ is the optimum of

$$\underset{V}{\min }\sum _{t=1}^T{\frac{1}{2}\left|\right|v_t-z_t\left|\right|}_2^2+{\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}+{\lambda }_t\sum _{t=1}^{T-1}{\left|\left|v_{t+1}-v_t\right|\right|}_1$$ (10)

It is straightforward to verify that Equation (10) is convex but non-smooth because of L21-norm and Fused Lasso regularization term. The basic idea to solve this problem is to use a smooth function to approximate the original non-smooth objective function. In this study, we use the Nesterov’s accelerated proximal gradient (APG) algorithm (Beck and Teboulle, 2009; Chen et al., 2009) to solve our optimization problem, which is shown in the Algorithm 1.

First, we separate Equation (10) into a smooth part Equation (11) and a non-smooth part Equation (12) as follows:

$$f\left(V\right)\sum _{t=1}^T{\frac{1}{2}\left|\right|v_t-z_t\left|\right|}_2^2$$ (11)

$$g\left(V\right)={\lambda }_v{\left|\left|V\right|\right|}_{\mathrm{2,1}}+{\lambda }_t\sum _{t=1}^{T-1}{\left|\left|v_{t+1}-v_t\right|\right|}_1$$ (12)

We define the approximation function Equation (10) as follows, which is composited by the above smooth part and non-smooth one:

$$\Omega \left(V,V_i\right)=f\left(V_i\right)+<{V-V}_i,\nabla f\left(V_i\right)>+\frac{l}{2}{\left|\right|{V-V}_i\left|\right|}_F^2+g\left(V\right)$$ (13)

where ${\left|\right|·\left|\right|}_F^2$ denotes the Frobenius norm, $\nabla f\left(V_i\right)$ denotes the gradient of $f\left(V\right)$ on point $V_i$ at the $i$th iteration, and $\mathrm{l}$ is the step size. Finally, the update step of Nesterov’s APG is defined as:

$$V_{i+1}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{V}{\min }\frac{1}{2}{\left|\left|V-W\right|\right|}_F^2+\frac{1}{l}g\left(V\right)$$ (14)

where $W=V_i-\frac{1}{l}\nabla f\left(V_i\right)$. The key of APG algorithm is how to solve the update step efficiently. In addition, according to the technique used in Chen et al. (2009), instead of performing gradient descent based on $V_i$, we compute the search point as:

$$Q_i=V_i+{\alpha }_i(V_i-V_{i-1})$$ (15)

where ${\alpha }_i=\frac{{\rho }_{i-1}-1}{{\rho }_i}$ and ${\rho }_i=\frac{1+\sqrt{1\hspace{0.5em}+\hspace{0.5em}4{\rho }_{i-1}^2}}{2}$. For more details about the solution of L21-norm and Fused Lasso problem, please refer to the previous work (Jie et al., 2016; Liu et al., 2010).

Algorithm 1.

 Input: SNPs $X={[x_1,\dots ,x_n,\dots ,x_N]}^{\mathrm{T}}\in R^{N\times p}$; longitudinal imaging phenotypes$\mathrm{ }{Y}_t={[y_{1t},\dots ,y_{nt},\dots ,y_{Nt}]}^{\mathrm{T}}\in R^{N\times q}$ at time-point $t$ ($1\le t\le T$); parameters ${\lambda }_u>0$, $\theta >0$, ${\lambda }_v>0$, ${\lambda }_t>0$.

 Initialization:${l=l}_0=1$, $V_0=V_1=0$, ${\rho }_0=1$.

 While not converge do

  1: Calculate the diagonal matrix $D$, where the $k$-th element is $1/2{\left|\right|u^k\left|\right|}_1$;

  2: Update $u$ by Equation (8);

  3: Scale $u$ so that ${\left|\right|Xu\left|\right|}_2^2=1$;

  4: Computed the search point $Q_i$ according to Equation (15);

 5:Find the smallest $l=l_{i-1},{2l}_{i-1},\dots$ so that $\Omega \left(V_{i+1},Q_i\right)\le f\left(V_{i+1}\right)+g\left(V_{i+1}\right)$, where $V_{i+1}$ is computed by Equation (14);

  6: Set $l_i=l$;

  7: Scale $v_t$ so that ${\left|\right|Y_t{v}_t\left|\right|}_2^2=1$.

 End while

 Output: canonical vector $u\in R^{p\times 1},\mathrm{ }V=[{v_1,\dots ,v}_t,\dots ,v_T]\in R^{q\times T}$.

3 Results and discussions

3.1 Results on simulation data

In this section, we present a simulation study to evaluate the potential power of our proposed TGSCCA method. The procedure of simulation generation is similar to that in Chen et al. (2012)and Fang et al. (2016). We first generated one canonical vector $u$ with p’ non-zero entries and successive canonical vector $v_k$ with q’ non-entries, where $v_{k+1}=v_k+\Delta v\mathrm{ }(\Delta v\sim N\left(0,\mathrm{ }0.1\right)\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }(k=\mathrm{1,2},3\left)\right)$. Each non-zero variable in $u$ and $v_1$ was sampled independently from a uniform distribution in the range of $\left[-2,\hspace{0.5em}-0.5\right]\cup [0.5,\mathrm{ }2]$. And then, we randomly generated a latent variable $h$ with normal distribution $N(0,\mathrm{ }{\sigma }_h)$ for each sample, where ${\sigma }_h$ is the signal to noise level. For the data matrix X and Y, the features were simulated from Gaussian distribution $N(uh,{{\sigma }_{e}I}_p)$ and $N(v_{k}h,{\sigma }_e{I}_q)$, respectively. We set N = 100, p = 100, q = 50, p’=30, q’=20, ${\sigma }_h=0.1$. To validate the effects on the performance, we varied the noise level ${\sigma }_e$ from 0.1 to 0.5 to generate simulation data 1 and simulation data 2, respectively.

In our experiments, 5-fold cross-validation strategy is adopted to evaluate the effectiveness of our proposed method. All the regularization parameters are optimally tuned using a grid search from the range of {0.01, 0.02, 0.05, 0.08, 0.1, 0.2, 0.5, 0.8, 1} by another nested 5-fold cross-validation on the training set.

We compare SCCA (denoted as sparse canonical correlation analysis to detect associations between SNP loci and imaging features at each time-point), GSCCA (denoted as group sparse canonical correlation analysis to detect associations between SNP loci and longitudinal imaging phenotypic features jointly across all time-points only via L21-norm), and TGSCCA (denoted as temporally-constrained group sparse canonical correlation analysis to detect associations between SNP loci and longitudinal imaging features jointly across all adjacent time-points via L21-norm and fused penalty).

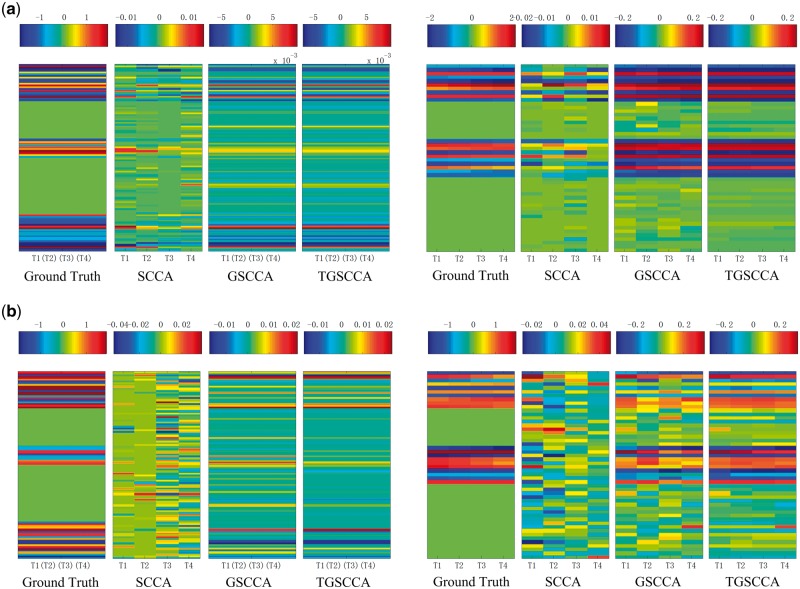
The performance on each dataset is assessed with correlation coefficient between X and Y, which are widely used in measuring performances of association analysis. The average results of correlation coefficients on 5-fold testing data are calculated respectively on Simulation 1 and Simulation 2. As shown in Figure 2, joint longitudinal association methods (including GSCCA and TGSCCA) outperform SCCA consistently and significantly in the metrics of correlation coefficients on both simulations. It is worth noting that TGSCCA is comparable with GSCCA due to the low noises in Simulation 1, while TGSCCA is more robust to the data with high noises in Simulation 2. Furthermore, we show the estimated canonical weights from different methods. As shown in Figure 3, the overall profiles of the estimated u and v values from TGSCCA are consistent with the ground truth on both Simulation 1 and Simulation 2, whereas SCCA is only capable of identifying inconsistent signals at different time-points. Although GSCCA can almost capture the same signals on u as TGSCCA, from the unsmooth patterns across the longitudinal case, it may be affected by noises and then draw false discoveries on v without the induced temporal-constraint. From the above results, it is observed that TGSCCA can identify not only the signal locations but also strong correlations, which has certain superiority compared with other methods.

Fig. 2.

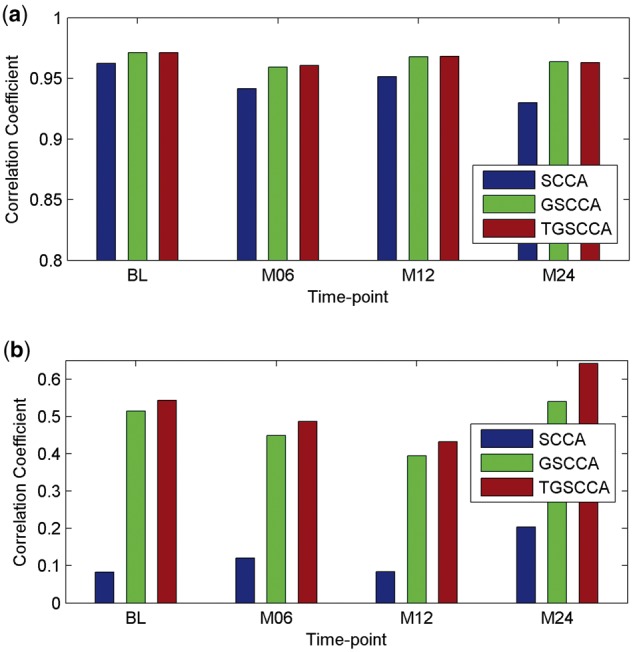
The averaged correlation coefficients on 5-fold test data using different methods on simulations. (a) Results on simulation data 1. (b) Results on simulation data 2

Fig. 3.

The estimated weights of u and v from average 5-fold cross-validation test on simulation data are shown in the left five panels and right five panels. Ground truth of w and v are shown in the most left in the two parts, respectively. The estimated u values and v values are shown in the remaining panels, corresponding to different methods. (a) Results on simulation data 1. (b) Results on simulation data 2

3.2 Results on real imaging genetic data

3.2.1 ADNI dataset

Real imaging genetics data used in the preparation of this article were obtained from the ADNI database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org.

The genotyping and longitudinal imaging data of 114 non-Hispanic Caucasian participants were downloaded from the ADNI website. The demographic information is summarized in Table 1. Specifically, the time points examined in this study for MRI T1-weighted imaging and cognitive assessments (i.e., MMSE and ADAS-Cog) included baseline (BL), Month 06 (M06), Month 12 (M12) and Month 24 (M24). We aligned the preprocessed imaging data [i.e., voxel based morphometry (VBM)] to each participant’s same visit scan, and then created normalized gray matter density maps from MRI data in the standard Montreal Neurological Institute (MNI) space as 2 × 2 × 2 mm³ voxels SPM software package (Ashburner and Friston, 2007). One hundred and sixteen ROI level measurements of mean gray matter densities were further extracted based on the MarsBaR AAL atlas (Tzourio-Mazoyer et al., 2002). After removal of cerebellum, the imaging measures of 90 ROIs were used as phenotypes in our experiments. For the genotyping data, we included 85 SNPs within ±20k base pairs of the APOE gene boundary based on the ANNOVAR (http://annovar.openbioinformatics.org) annotation. For input in this association study, each SNP value was coded in an additive fashion as 0, 1, 2, indicating the number of minor alleles.

Table 1.

Demographic characteristics of the studied population (the values are denoted as mean ± standard deviation)

Subjects	pMCI (n = 15)	sMCI (n = 41)	NC (n = 58)
Gender (M/F)	8/7	26/15	31/27
Age	71.75±5.92	73.40±7.59	75.71±4.74
Education	16.33±3.54	16.22±2.86	16.38±2.85
MMSE(BL)	26.93±1.91	27.59±1.50	29.21±0.99
MMSE(M06)	26.07±2.69	27.59±1.76	29.03±1.03
MMSE(M12)	25.47±2.72	27.56±1.91	29.38±0.83
MMSE(M24)	22.80±4.00	27.61±2.24	29.12±1.09
ADAS-Cog(BL)	20.64±5.51	15.45±5.80	8.92±3.69
ADAS-Cog(M06)	22.91±8.48	15.52±5.77	8.95±3.75
ADAS-Cog(M12)	24.33±6.57	15.20±5.93	7.58±4.05
ADAS-Cog(M24)	26.95±8.07	16.11±6.28	8.43±4.43

Note: NC = Normal Control, pMCI = progressive Mild Cognitive Impairment, sMCI = stable Mild Cognitive Impairment, MMSE = Mini-Mental State Examination, ADAS-Cog = Alzheimer’s Disease Assessment Scale-Cognitive Subscale.

3.2.2 Improved association between risk SNP loci and longitudinal imaging ROI markers

In the real data experiments, we also use 5-fold cross-validation strategy to evaluate the effectiveness of our proposed method. Similar to the previous simulation study, we determine the values of regularization parameters by nested 5-fold cross-validation on the training set. The parameters are tuned in the range of {0.01, 0.02, 0.05, 0.08, 0.1, 0.2, 0.5, 0.8, 1}.

In current studies, we compare our proposed joint longitudinal imaging genetic strategies (including GSCCA and TGSCCA) with conventional SCCA method. For measuring the association performance of the compared methods, the average values of Pearson correlation coefficients on 5-fold test sets are calculated to eliminate the bias. As shown in Figure 4, the performances of longitudinal strategies with joint detections (including GSCCA and TGSCCA) are more stable than the conventional SCCA, which treats imaging genetic associations at each time-point independently. As expected, TGSCCA can achieve the best correlation coefficients so that it consistently outperform SCCA and GSCCA. These results demonstrate that the usage of temporal information across adjacent time-points can help improve the performances of association between genotypes and longitudinal imaging phenotypes.

Fig. 4.

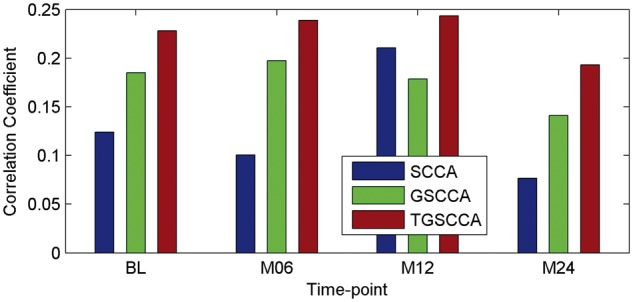
The averaged correlation coefficients on 5-fold test data using different methods on ADNI

3.2.3 Identification of risk SNP loci

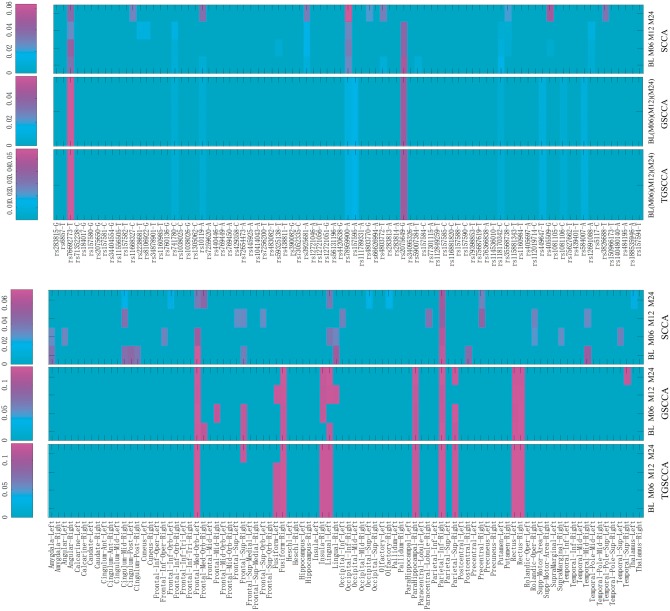
Besides improving association performance, one major goal of this study is to identify some vital SNP loci and imaging phenotypic markers for disease progression in MCI research. Therefore, finding genetic risk factors and imaging ROIs helps scientists better understand how the disease develops and identify possible treatments to study. We aim to present the selected features on the SNP loci and imaging ROIs, whose annotations are shown on the X-axis from top and bottom panels in Figure 5. It shows all comparisons of absolute weight maps for top 10 loci from APOE SNPs associated to top 10 brain ROIs with longitudinal analysis respect to different methods.

Fig. 5.

The estimated weights of u (top panels) and v (bottom panels) from average 5-fold cross-validation test on ADNI data using the different methods

For detecting genetic factors, as shown on top panels in Figure 5, the locus rs76692773 and rs2075649 (Lin et al., 2016) are the top hits by all methods. However, compared with SCCA, the joint longitudinal detections (including GSCCA and TGSCCA) can discover consistent and clear patterns across all time-points, which indicate our proposed method performs stable in longitudinal imaging genetic associations. It is worth noting that the best-known risk genetic loci rs429358 has not been identified by all methods (including our proposed TGSCCA). It warrants further investigation to confirm whether the eminent risk factor rs429358 is truly not associated with longitudinal VBM phenotypes in the MCI progression. In addition, as the association solution relies on the linear combination of all loci, an individual one might not have a direct influence to the correlation, i.e., it might modulate the influence of another locus. Consequently, these genetic factors selected in this association study should also warrant further investigation for replication in independent and larger cohorts.

3.2.4 Identification of longitudinal imaging ROI markers

For detecting brain imaging ROIs, as shown on bottom panels in Figure 5, the conventional SCCA method identifies some irregular imaging ROIs at different time-points, which are not able to serve screening target over the course of MCI progression. While using joint longitudinal detection strategies, we can obtain clear patterns on the feature panels. For example, right parahippocampal gyrus and right superior parietal gyrus are the two top hits in joint detections (including GSCCA and TGSCCA), which are in accordance with previous findings (Jacobs et al., 2012; Shen et al., 2010). In addition, the top ROIs selected for progression across all time-points by TGSCCA can be treated as increasingly stable markers, which are also accordance with the fact that the grey matter atrophy of these ROIs is severe in MCI (Driscoll et al., 2009). Therefore, compared with SCCA and GSCCA, our proposed TGSCCA can tolerate noises to some extent so that the weight maps of each selected ROI across different time-points are very smooth. This further indicates the advantage of using the temporal-constrained smoothness regularization.

4 Conclusion

In this article, we propose a novel TGSCCA framework to detect risk genetic factors and their correlated longitudinal phenotype markers for a progressive disease (i.e., MCI). This approach explicitly captures the consecutive changes between phenotypes from adjacent time-points by incorporating the group sparsity constraint and fused penalty into the objective function. We also present an effective iterative algorithm to solve the optimization problem. We apply the proposed method on the simulation data and ADNI cohort [including progressive mild cognitive impairment (pMCI), stable MCI (sMCI) and NC participants]. The experimental results show that our proposed TGSCCA model can identify stronger associations than conventional SCCA and GSCCA. Besides the improved association performance, in real imaging genetic data, our model can also detect the risk SNP loci and clearly consistent brain ROIs across all time-points, which provides valuable information to help understand the genetic basis of brain structural change over the progression of MCI and AD.

As an interesting future direction, this TGSCCA method can be applied to investigate the potential mechanism of other imaging phenotypes (e.g., fluorodeoxyglucose positron emission tomography (FDG-PET) and Florbetapir F 18 amyloid PET data) (Hao et al., 2016) and biomarkers such as cerebrospinal fluid and plasma from longitudinal perspective (Fagan et al., 2014). Therefore, all kinds of biomarker outcomes learned from trajectories across the course of disease can be evaluated, and the findings may have the potential to help with neurodegenerative assessments in clinical practices.

In this initial study, the proposed TGSCCA can be successfully applied for longitudinal imaging genetics study on a candidate gene set. However, when the datasets contain more features, it becomes more challenging to identify truly relevant ones. Thus, an interesting future direction could be to develop an improved TGSCCA model by exploring non-convex penalty terms that have been shown to be more effective than L1 based terms in terms of feature selection via sparse learning. In addition, this general framework can be extended and applied to some other interesting fields such as brain-perceived analysis (Connolly et al., 2016) and gene expression analysis on multiple data sources (Allahyar and de Ridder, 2015; Bunte et al., 2016; Omranian et al., 2016), allowing for generating new insights.