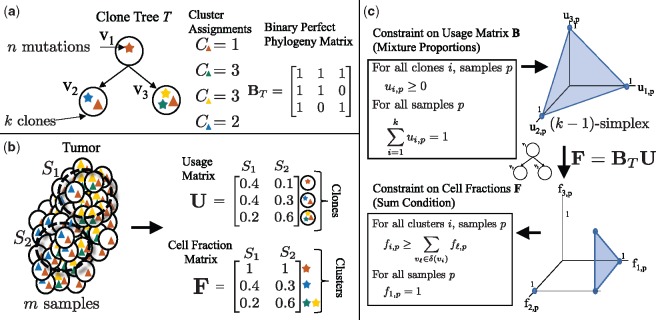
Fig. 1.

Tree constraint on cluster cell fractions. (a) We model the evolution of a tumor as a clone tree T, with k vertices corresponding to clones in the tumor. A mutation (denoted here by a star) is assigned to the clone in which it originates. Under the infinite sites assumption, a mutation occurs once, and is never lost. Thus, if a mutation occurs in clone v_i, all descendent clones of v_i will also contain that mutation. A clone tree T can be described by a binary perfect phylogeny matrix B_T. (b) We measure m samples from a heterogeneous tumor, each sample containing a mixture of clones. The usage matrix U describes the proportion of each clone in each sample. The cell fraction matrix F describes the proportion of cells that contain a given cluster of mutations. For example, here the clone v₁, containing the red mutation, occurs in $u_{1,1}=40\%$ of sample S₁, but has a cell fraction of $f_{1,1}=1$, as the red mutation is present in all cells. (c) As the usage matrix U describes mixture proportions, the columns of U are constrained to be on the $(k-1)$-simplex. For a tree T, F and U are related by F = B_TU. Thus, the set of allowed cell fractions for a tree T is a linear transformation of the $(k-1)$-simplex and is unique for every distinct tree T. This set can be described by the Sum Condition, where $\delta (v_i)$ denotes the set of children of v_i in T