Fig. 6.

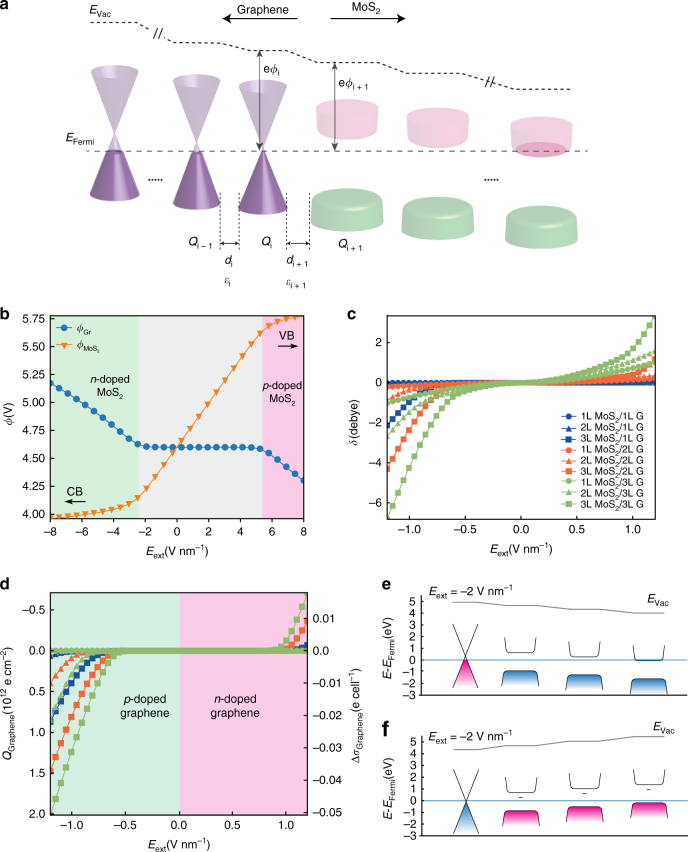
Classical electrostatic approach for charge redistribution of MoS₂/Graphene vdW heterostructures. a Schematic band diagram of the multilayer MoS₂/Graphene heterostructures. Vacuum level (E_vac), work function (${\varphi }_i$), surface charge density (Q_i), interlayer distance (d_i), and relative permittivity (ε_i) are shown for each stacking i. b Work functions of graphene and MoS₂ as functions of external electric field E_ext (V nm⁻¹). The regimes of the n-doped and p-doped MoS₂ are highlighted in green and faint red, respectively. The Fermi level reaches the conduction band (CB) or valence band (VB) of MoS₂ when large negative or positive E_ext is applied, relatively (as shown by the arrows). c Electric dipole moment δ (Debye) as a function of E_ext (V nm⁻¹) for different number of graphene and MoS₂ layers on the heterostructures. d Surface charge density Q_Graphene (left axis) and the amount of charge transfer between graphene and MoS₂ layers Δσ_Graphene (right axis) as a function of E_ext (V nm⁻¹) for different MoS₂/Graphene systems. The curves follow the labeling in (c). e–f Band alignments for an illustrative case, e.g., 3L MoS₂ /1 L Graphene under −2.0 V nm⁻¹ and +2.0 V nm⁻¹ electric fields, respectively. Positive charges are shown in faint red and negative charges are shown in blue, respectively. Only band structures near the Fermi level are shown for illustration