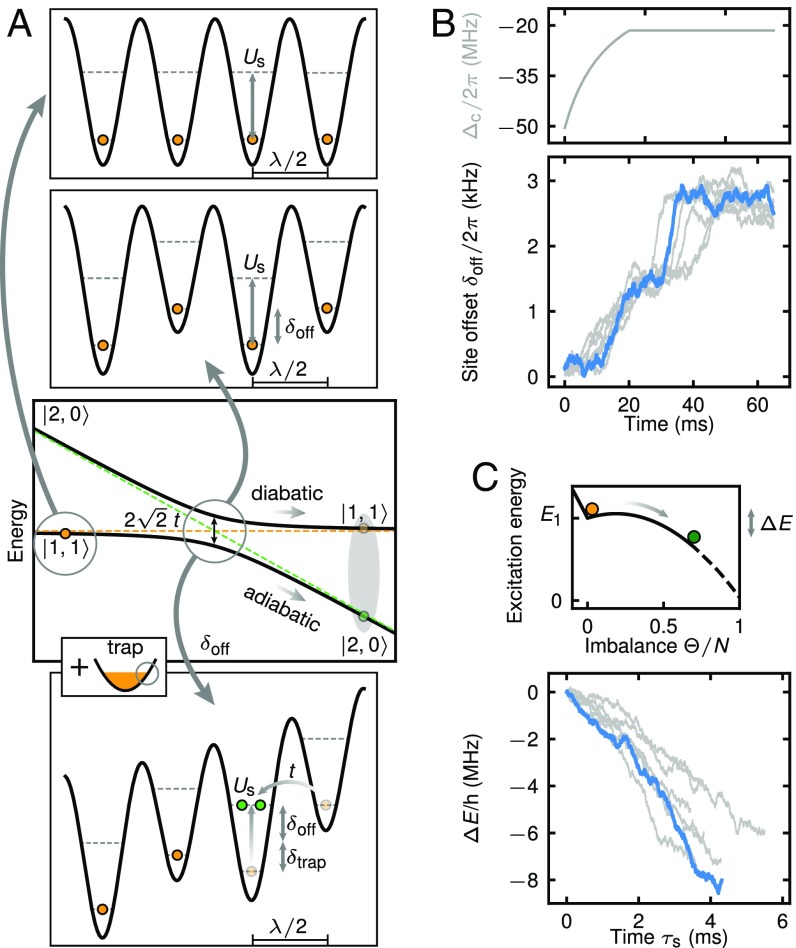
Fig. 5.

Microscopic dynamics and energy redistribution of the system. (A) Microscopic description of the system dynamics following the detuning quench, in terms of a Landau–Zener transition. One-dimensional lattice potentials are shown for a normal lattice (Top), a dynamic superlattice with site offset ${\delta }_{\text{off}}$ generated by superfluid surface atoms (Middle), and a tilted dynamic superlattice with spatially varying site offset ${\delta }_{\text{off}}+{\delta }_{\text{trap}}$ as encountered at the edge of the harmonic trap (Bottom). Colored circles represent atoms in the states $|\mathrm{1,1}⟩$ (orange) or $|\mathrm{2,0}⟩$ (green). Resonant nearest-neighbor tunneling is allowed when the site offset ${\delta }_{\text{off}}+{\delta }_{\text{trap}}$ equals the short-range interaction strength $U_{\text{𝗌}}$. (B) Dynamics of the site offset ${\delta }_{\text{off}}$ in the metastability measurement. (C, Top) Sketch of the excitation energy of the bulk atoms. Superfluid surface atoms add a symmetry-breaking field to the toy model. During the imbalance jump (ii), the highly excited system reduces the initial excitation energy $E_1$ via an avalanche of inherently nonadiabatic Landau-Zener transitions by an amount of $\mathrm{\Delta }E$. Colored circles represent the state of the system, where the MI state (orange) results from all bulk atoms in the $|\mathrm{1,1}⟩$ state and the CDW state (green) from atoms being in a superposition of $|\mathrm{1,1}⟩$ and $|\mathrm{2,0}⟩$ states. Accordingly, the relative imbalance saturates at $\mathrm{\Theta }/N<1$, indicated by the dashed line. (C, Bottom) Reduction of $\mathrm{\Delta }E$ as a function of time ${\tau }_{\text{s}}$ during the imbalance jump (ii). (B and C) Exemplary traces use the same data as shown in Fig. 4. ${\delta }_{\text{off}}$ and $\mathrm{\Delta }E$ are inferred from the photon flux leaking from the cavity.