Fig. 1.

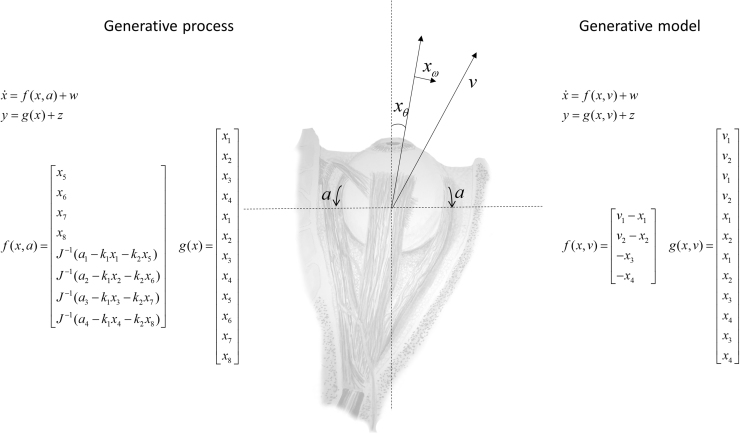
Equations of motion This schematic shows the equations used to determine the motion of the eyes, and the sensations they generate. On the left, the pair of equations defining the ‘real-world’ generative process are shown. On the right, the analogous equations are shown for a generative model of that process. Note that the dimension of the sensory data, $y$, is equal for both, but the dimensions of the hidden states, $x$, differ. In the generative process, $x_{1,2,3,4}$ are the (2 × 2) angular horizontal and vertical positions for the right and left eye (components of the $x_{\theta }$ vectors). $x_{5,6,7,8}$ are the angular velocities (components of the $x_{\omega }$ vectors). Each of these is associated with a result torque involving the extraocular muscles, $a_{1,2,3,4}$, an elastic torque with spring constant $k_1$, and a viscous torque with a viscosity constant $k_2$. The resultant torque is converted to acceleration through division by the moment of inertia of the eyeballs $J$. In the generative model, $x_{1,2}$ are the horizontal and vertical positions of both eyes, which are crucially assumed to be the same. $x_{3,4}$ are the velocities. $v_{1,2}$ are the two components of the target fixation vector. $w$ and $z$ are random Gaussian fluctuations with means of zero and precisions of ${\Pi }_x$ and ${\Pi }_y$ respectively.