Evaluating models for polycaprolactone crystallization via simultaneous rheology and Raman spectroscopy

Abstract

The crystallization of a polymer melt is characterized by dramatic structural and mechanical changes that significantly impact the processing conditions used to generate industrially-relevant products. Relationships between crystallinity and rheology are necessary to simulate and monitor the effect of processing conditions on the properties of the final product. However, separate measurements of crystallinity and rheology are difficult to correlate due to differences in sample history, geometry, and temperature. Recently, we have developed a rheo-Raman microscope for simultaneous rheology, Raman spectroscopy, and polarized reflection-mode optical measurements of soft materials, which allows for quantitative crystallinity measurements through features in the Raman spectrum. In this work, we apply this technique to monitor the isothermal crystallization of polycaprolactone to probe the relationship between structure, crystallinity, and rheology. Both crystallinity and the shear modulus vary over comparable timescales, but the birefringence increases much earlier in the crystallization process. We directly plot rheological parameters as a function of crystallinity to probe a range of suspension-based and empirical models relating the complex modulus to crystallinity, and we find that the previously developed models cannot describe the crystallinity-modulus relationship over the crystallization process. By developing a suspension-based model we can fit the complex modulus over the crystallization range. The crystallization process is characterized by a critical percolation fraction and a single scaling exponent.

Introduction

When a polymer crystallizes, it undergoes a dramatic transition from an amorphous melt to a hierarchically-organized semicrystalline structure. This structural transition is accompanied by an increase in the mechanical properties of the polymer, e.g., the storage modulus increases by many orders of magnitude [1]. This effect is exploited in conventional polymer processing techniques such as fiber spinning or blow molding [2], and it is also used heavily in additive manufacturing processes including filament extrusion and powder bed fusion [3]. The utilization of polymer crystallization is largely empirical during processing, but direct relationships to relate crystallinity and rheological properties would be invaluable to the efficient processing of new materials.

Many models have been developed to relate crystallinity and rheology in semicrystalline polymers. Several empirical and suspension-based models have been summarized previously [4]. The simplest model assumes a linear relationship between the storage modulus and the crystallinity as proposed by Gauthier et al.[5] and has been used extensively to estimate the time evolution of crystallinity from rheological measurements [6–11]. However, a linear relationship between the logarithm of the storage modulus and crystallinity has also been used [12]. Other researchers have determined nonlinear relationships between crystallinity and the modulus through suspension-based models [13, 14]. Christensen and Lo[15, 16] developed a composite sphere model for viscoelastic suspensions that has been applied to crystallizing polyolefins [14, 17, 18]. The model predicts the complex modulus at any crystallinity when the complex shear moduli and Poisson ratios of the melt and semicrystalline phases are known. Pogodina and Winter proposed that crystallization proceeds as a gelation-type transition via frequency sweep measurements during crystallization [19], which allows for the determination of a gelation point but not the degree of crystallinity.

A primary challenge in determining the underlying crystallinity-modulus relationship is the difficulty in relating crystallinity and rheology measurements performed on separate instruments. There have been attempts to correlate rheology measurements with separate measurements from differential scanning calorimetry (DSC) [7, 19–22], optical microscopy [23], small angle light scattering [24], and wide angle X-ray diffraction [14]. These methods have been used to justify both empirical rules, suspension-based rules, and gelation-type models. The difficulty in relating these measurements is attributed to the sensitivity of crystallization kinetics to temperature and sample history [25].

Instrumentation has also been developed to provide simultaneous measurements of crystallinity and rheology by coupling a rheometer with optical imaging [26, 27], birefringence [28], nuclear magnetic resonance (NMR) [29], or DSC capabilities [30]. NMR and DSC measurements quantify the crystallinity of the entire sample volume on the rheometer, while optical imaging measures the growth of space-filling structures in a region within the sample. NMR measurements provide a direct measure of crystallinity by quantifying the relative amounts of rigid and mobile phases in crystallizing polymers, but the analysis can be complicated by mobile chains in crystalline domains as observed in polyethylenes [31]. Quantitative crystallization information is often difficult to obtain from DSC measurements due to the presence of simultaneous thermal processes (crosslinking or degradation) during the crystallization process. Optical imaging allows for the direct observation of local structure growth, but sample turbidity will often obscure structural details at higher crystallinities. Birefringence has been shown to correlate with crystallinity [28], although polarized light scattering measurements in combination with Raman spectroscopy have shown that turbidity and light depolarization can occur well before the appearance of crystallinity [32]. There is a clear need for instrumentation that can provide a nondestructive crystallinity measurement for a wide range of polymers over the entire crystallization process.

Recently, we have developed an instrument for simultaneous rheology, optical microscopy, and Raman spectroscopy called the rheo-Raman microscope [33]. This instrument can perform polarized reflection-mode optical imaging and Raman measurements within a sample on the rheometer using either parallel plate or cone and plate geometries. Raman spectroscopy measures a range of vibrational modes that are attributed to chemical information such as molecular conformation, bond formation/scission, and chemical composition. Changes in this chemical information often accompany a change in the rheology of a material, and simultaneous rheology and Raman spectroscopy measurements have been implemented to monitor agarose gelation [34], free-radical polymerization [35], and epoxy curing [36]. When combined with polarized optical microscopy, we gain additional structural insight into the process under investigation: for example, we have shown that birefringent structure growth precedes changes in the rheology and the Raman spectrum of a crystallizing polyethylene [37].

Here, we use the rheo-Raman microscope to monitor the crystallization of polycaprolactone (PCL), an aliphatic polyester that is often used in additive manufacturing. The ease of functionalization allows PCL to be made more biocompatible for printing cell and tissue scaffolds from extrusion-type printing processes [38]. We have recently analyzed the Raman spectrum of PCL to distinguish the features that indicate crystallinity from spectral features due to single-chain order [37]. Our results showed that the carbonyl (C=O) stretch region of the spectrum contains spectral features attributed to chains in a crystalline packing that can be directly correlated with DSC-measured crystallinities. This analysis allows for a direct non-destructive measurement of crystallinity to be performed via Raman spectroscopy during a rheological measurement.

In this work, we simultaneously measure the Raman spectra and oscillatory shear rheology of PCL crystallizing isothermally. Our measurements allow us to plot rheological parameters as a function of crystallinity to determine the sensitivity of the modulus to incremental addition of semicrystalline material. Additionally, this allows us to directly probe numerous modulus-crystallinity models proposed in the literature, both suspension-based models and the empirically-developed mixing rules. We find that these models do not correlate with experimental results. Given this situation, we model the system using suspension-type models across a percolation threshold to develop a relationship between crystallinity and the complex modulus that is applicable over the entire crystallization process.

Experimental Section

Poly-ε-caprolactone (PCL) was received in pellet form (CAPA 6500, Perstorp) and used without purification. The equilibrium melting temperature of PCL is 69.2 °C [39]. Gel permeation chromatography was used to measure the molar mass distribution of the polymer dissolved in tetrahydrofuran. The column was calibrated at 30 °C by using narrow polydispersity polystyrene (PS) standards, and the molar mass of PCL was calculated by using the following Mark-Houwink parameters: K_PS = 2.90 × 10⁻⁸ m³/g, a_PS = 0.634, K_PCL = 3.06 × 10⁻⁸ m³/g, a_PCL = 0.70 [40]. The number-average molar mass of PCL used in this work is 55.8 kg/mol and the mass-average molar mass is 96.6 kg/mol to within an uncertainty of 10% (see Disclaimer in Acknowledgements).

The rheology, Raman spectroscopy, and polarized reflection mode microscopy measurements were performed using a rheo-Raman microscope (Thermo Fisher) [33]. Pellets were melt-pressed at 100 °C for 300 s into 1 mm thick sheets, and samples were punched out using a 3 mm radius brass hole punch. The samples were loaded at 100 °C (approximately 30 °C above the equilibrium melting temperature) into an 8 mm parallel plate geometry at a gap thickness of 300 μm. All measurements were performed in air. Samples held at 100 °C exhibited a constant modulus (ω = 6.28 rad/s) over a period of 7200 s, which indicates negligible thermal degradation over relevant timescales for the measurements shown in this work. After sample loading the temperature was kept at 100 °C for 300 s to remove melt memory effects. Holding the sample at 100 °C for less time (30 s) led to faster crystallization at 40 °C, but increasing the time to 1000 s did not slow the kinetics further. A series of two temperature ramps were used to cool the sample to a crystallization temperature (T_c): an initial ramp at a rate of 0.167 °C/s from 100 °C to T_c + 10 °C, then a slower temperature ramp at 0.033 °C/s from T_c + 10 °C to T_c. Oscillatory rheology measurements were performed at T_c in a constant strain mode controlled by a feedback loop within the instrumentation. All measurements were performed at a frequency of 6.28 rad/s, and three oscillations are used to measure the modulus at each time point during crystallization. We performed a strain amplitude sweep in both the melt and semicrystalline states to determine a strain amplitude within the linear viscoelastic region over the entire crystallization process. A linear viscoelastic range is found between strains of 0.001 and 0.005 in both states (see Supplementary Material), and based on these measurements we choose a strain amplitude of 0.004 for the crystallization measurements. Results are reported in terms of the storage modulus G′ and the loss modulus G″ or the magnitude of the complex modulus, $\left|G\ast \right|=\sqrt{{\left(G^{\prime }\right)}^2+{\left(G^{″}\right)}^2}$, and the phase angle δ as tan δ = G″/G′.

Raman spectroscopy measurements were performed using a 532 nm excitation wavelength at the instrument maximum power of 10 mW focused through a 10× objective into the sample. Two exposures of 15 s duration are averaged together to generate the spectrum, and the subsequent polarized optical imaging blocks laser light from the sample for 2 s. Longer spectra collection times would increase the signal-to-noise ratio in the spectrum but also decrease the number of measurements during the crystallization process. This would lead to large uncertainty in the fitting parameters for the modulus-crystallinity analysis presented in this work and is avoided here.

Sample Raman spectra are shown in Figure 1. The C=O stretch region of the spectrum is fit using three basis spectra attributed to different chain conformers [37]: a random coil chain conformation (“random coil”); an otherwise structureless coil with C=O bonds on neighboring chains oriented antiparallel to each other due to dipole-dipole interactions (“dipole”); and ordered chains packed into the crystal lattice (“crystalline”). The line shape and relative position of each basis spectrum was determined through prior multivariate analysis [37]. The fitting procedure seeks a best fit to the experimental spectrum by varying the three basis spectra intensities, a single shift factor to account for instrument accuracy in the Raman shift, a linear background slope, and a constant offset. These six parameters are fit simultaneously using a nonlinear least-squares regression, and the best fit results of the Raman spectra are independent of the initial parameter estimation. The C=O stretch region of the spectrum in the melt state is shown in Figure 1a – it is well fit by the basis spectra associated with dipole-dipole interactions and a random coil chain conformation, with a negligible contribution from the crystalline peak. The spectrum of PCL after crystallization (Figure 1b) is instead best fit by a combination of all three basis spectra. The crystalline basis spectrum contributes significantly to the overall peak shape, while the random coil chain conformer is reduced compared to the melt spectrum.

Figure 1.

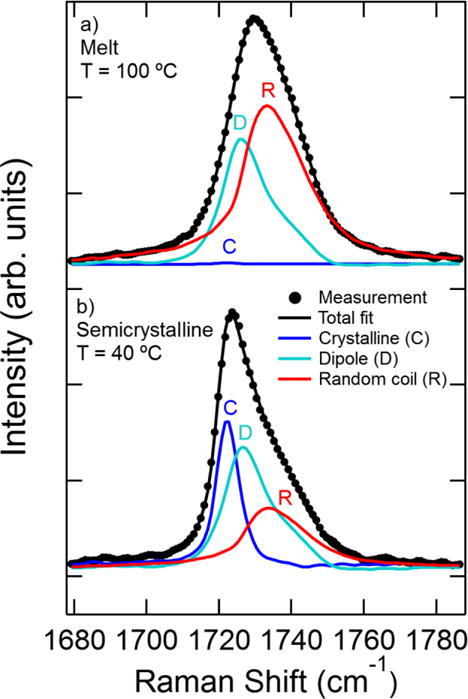
Raman spectrum of PCL in the C=O stretch region of the spectrum and fits of basis spectra for two different conditions: a) “Melt” at 100 °C and b) “Semicrystalline” at 40 °C after crystallization for 1960 s. The measured crystallinity in the semicrystalline spectrum is α_c = 0.40 ± 0.02 where the uncertainty is due to the statistical uncertainty in the best-fit basis spectra to the measured spectrum.

The mass fraction of crystalline material is calculated based on the normalized integrated intensity of the crystalline basis spectra I_cr fit to each spectrum. The crystallinity α_c is then

$${\alpha }_{\mathrm{c}}=\beta \frac{I_{\text{cr}}}{I_{\text{tot}}}$$ (1)

where I_tot is the sum of the integrated intensities of the crystalline, dipole, and random coil basis spectra. The prefactor β = 1.26 was determined in our prior work by a comparison of the crystallinity measured by DSC (accounting for finite crystal thickness [41]) and the peak intensity ratio I_cr/I_tot for 8 polycaprolactones of different molecular weights with crystallinities ranging from 51% to 84% [37]. We perform a linear least squares regression of the data assuming a relationship of the form α_c = β(I_cr/I_tot)+C, where β and C are the best fit coefficients. The best fit values are β = 1.26 and C = 0, which gives eq 1.

Polarized reflected light microscopy was also performed on the rheo-Raman microscope using the 10× objective. Images are taken immediately following each Raman spectrum, and the average pixel intensity is calculated in a 60 μm × 90 μm window centered on the region where the laser spot is focused. The images were also used to assess laser heating from the Raman spectra measurements. Since the material in the laser spot would be at a higher temperature on average, significant laser heating would cause the laser spot region to crystallize more slowly and exhibit birefringence at later times compared to the rest of the image. However, birefringence did not appear more slowly in the spot region, and so we assume laser heating is negligible in these experiments.

Separate isothermal crystallization measurements were performed in a Linkam shear cell (CSS450, Linkam Scientific) on a polarized light microscope (BX-51, Olympus). The sample was compressed to a thickness of 25 μm prior to measurement. Imaging was performed in transmission mode using a 50× objective (Olympus).

Results

Simultaneous measurements of the complex modulus G*, crystallinity α_c (via Raman spectroscopy), and polarized light intensity are shown in Figure 2 for isothermal crystallization at temperatures ranging from 40 °C to 44 °C. At temperatures below 40 °C we observe changes in the polarized light intensity prior to reaching the isothermal crystallization temperature. Measurements at temperatures greater than 44 °C showed a large variation in the crystallization kinetics measured via Raman spectroscopy, which we attribute to significant growth of semicrystalline regions outside the scattering volume of the laser. We find the crystallization process to be characterized mechanically by an initial slow increase in the modulus |G*|, followed by a more rapid increase in |G*| over orders of magnitude. At long times, there is a slow increase in |G*| where the modulus has a value on the order |G*| ≈ 10⁸ Pa. (These modulus values are measured at a torque of approximately 0.04 N · m, which is well below the 0.2 N · m instrument upper limit.) The initial values of tan δ are greater than 1, which indicates that the polymer is still in the melt state. The phase angle decreases to values much less than 1 as the modulus increases to indicate the solidification that occurs during the crystallization process. Experiments were also performed at a gap thickness of 1 mm to determine a potential gap dependence in our measurements, and we found that the timescales of the crystallization process occurred within a standard deviation of the measurement at the smaller gap size. For example, the crossover in tan δ for a 1 mm gap occurred at 550 s, which is well within the average range of 540 ± 44 s that was observed in a 300 μm gap.

Figure 2.

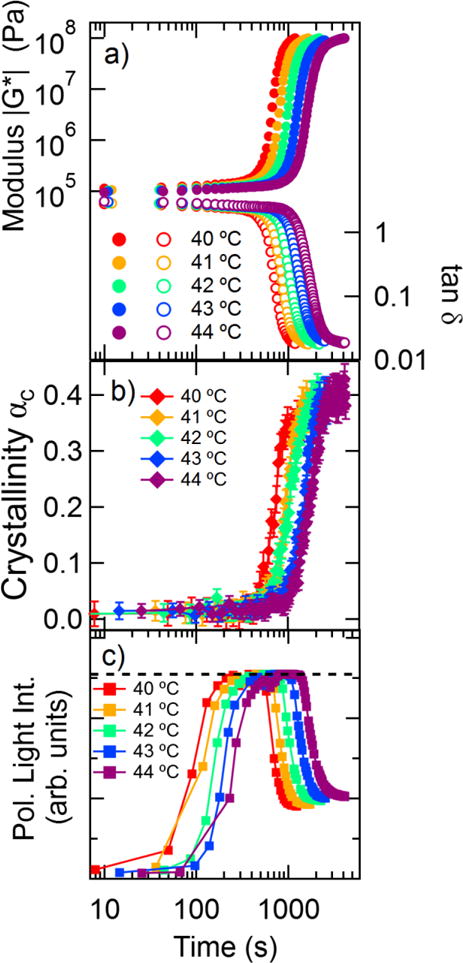
Isothermal crystallization of PCL at various temperatures. a) Magnitude of complex modulus and tan δ versus time. Measurements were performed at an angular frequency of 6.28 rad/s. b) Crystallinity measured from the Raman spectra versus time, with error bars based on the standard error in the fit of the basis spectra. c) Average polarized light intensity from polarized reflection microscopy versus time. The dashed line indicates the maximum intensity of detector. Error bars indicate uncertainty from the fits to the Raman spectra.

When measuring dynamic transitions via rheology, the timescale of each modulus measurement must be significantly faster than the timescale of the crystallization process. We can compare these timescales via the mutation number N_mu = t_exp∂(ln G′)/∂t introduced by Winter, where t_exp is the measurement time required to measure the modulus [19, 42]. Values of N_mu ≪ 1 are desirable to avoid systematic errors in the reported modulus. For our measurements the maximum N_mu is 0.07 at the lowest crystallization temperature, which indicates that the change in modulus during the measurement time is negligible. At higher crystallization temperatures the crystallization process proceeds more slowly.

The crystallinity as measured by Raman spectroscopy starts at negligible values, then increases measurably at times ranging from 400 s to 1000 s depending on the temperature. The crystallinity grows to mass fractions greater than 0.35 before transitioning to a period of slower crystallization. Despite the nonzero offset of approximately 0.02 in the crystallinity measurement at early times, the growth of crystallinity can be fit using a combination of the Avrami function plus a constant (see Supplementary Material). The fits to the crystallinity measurements indicate Avrami exponents in the range of 3.0 < n < 4.1 for the data shown in Figure 2b, which is near the value of n = 4 measured by dilatometry [43]. The Avrami exponent value is the sum of the dimensionality of the growing crystal (either 1, 2, or 3) and whether the nucleation process is homogeneous (add 1) or heterogeneous (add 0) [1]. An Avrami exponent of 4 is consistent with crystallization proceeding via homogeneous growth of three-dimensional structures.

The polarized light intensity from reflection mode microscopy in Figure 2c is more sensitive to the onset of crystallization than either rheology or Raman spectroscopy. The appearance of polarized light indicates the growth of birefringent structures within the sample, which is not accompanied by significant changes in the other measured parameters. After a period of time, the polarized light intensity decreases below the saturation level due to the continued growth of structures that cause significant turbidity and polarization scrambling. This change in the polarized light intensity as well as its appearance prior to changes in the modulus or crystallinity has been previously reported in polyethylene [33].

We do not observe any distinguishing structure using reflection mode imaging on the rheometer, and separate measurements in cross-polarized transmission optical microscopy did not reveal significant growth of spherulites during crystallization (see Supplementary Material for example images). Instead, a “grainy fog” structure appeared and increased in intensity during crystallization, decreasing only slightly from turbidity effects due to the smaller sample thickness. We note that the “grainy fog” grows with an apparent three-dimensional structure, which correlates well with the Avrami exponents 3 < n < 4 measured by Raman spectroscopy in this temperature range.

Our simultaneous measurements allow us to plot the measured rheological properties as a function of crystallinity to better test structure-property relationships between crystallinity and rheology. The modulus and crystallinity are sampled at different rates, therefore we interpolate the modulus data to find the estimated values at the times the crystallinity was measured. The modulus and tan δ can then be plotted as a function of crystallinity as shown in Figure 3. The modulus increases dramatically with crystallinity until a transition to slower crystallization kinetics in the approximate range of 0.35 < α_c < 0.4 for all temperatures. The point tan δ = 1 distinguishes the transition from a liquid-like state to a solid-like one at the measurement frequency; we note that this point occurs in the range of 0.06 < α_c < 0.13.

Figure 3.

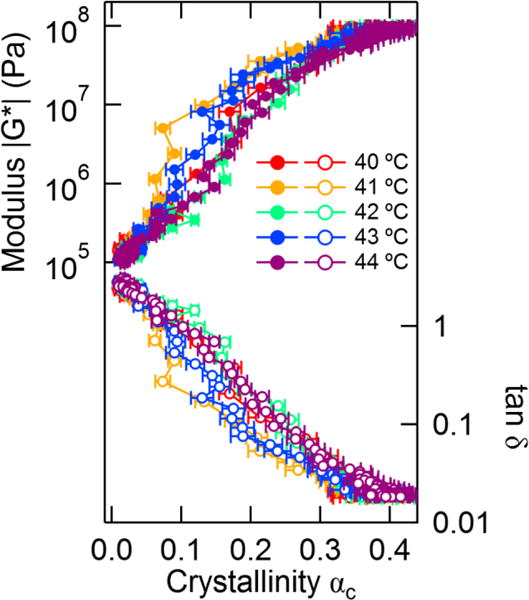
Modulus |G*| and tan δ data from Figure 3 plotted as a function of crystallinity. The filled symbols correspond to the modulus, and the open symbols indicate tan δ. Error bars indicate propagated uncertainty from the fits to the Raman spectra.

Modeling the Crystallinity-Modulus Relationship

Empirical Models

The data shown in Figure 3 can be used as a direct probe of the numerous modulus-crystallinity relationships available in the literature. We can divide these models into empirical models, composite-sphere models that determine the effective modulus of a particle embedded in a shell of matrix material, and hydrodynamic suspension models which assume that a crystallizing polymer melt can be modeled as a liquid with particle-like crystalline inclusions [4]. These suspension-based models treat the semicrystalline domains as solid particles that are evenly distributed and isotropically oriented with respect to each other. The modulus-crystallinity relationships are generally of the form

$$f\left(\mathrm{\Lambda },{\mathrm{\Lambda }}_{\mathrm{m}},{\mathrm{\Lambda }}_{\mathrm{s}}\text{or}{\mathrm{\Lambda }}_{\mathrm{\infty }},\varphi \text{or}\xi \right)=0$$ (2)

where Λ is a rate-dependent rheological material property. The subscript “m” in eq 2 refers to the melt, “s” refers to the solid phase, and ϕ is the crystalline volume fraction. A volume fraction of ϕ = 1 corresponds to a single polymer crystal. Volume fractions approaching unity are rarely (if ever) observed during crystallization, and many models utilize the relative volume fraction ξ = ϕ/ϕ_∞ sometimes referred to as a degree of space filling [14], where the subscript “∞” refers to the condition where the sample volume is filled with spherulites. Because Raman measurements are correlated with DSC measurements on a mass fraction basis, we convert the crystalline mass fractions to volume fractions by assuming that the crystallizing polymer is a two-phase system of melt and crystalline material using eq 3

$$\varphi =\frac{{\alpha }_{\mathrm{c}}}{{\alpha }_{\mathrm{c}}+\frac{v_m}{v_c}\left(1-{\alpha }_{\mathrm{c}}\right)}$$ (3)

where ν_m and ν_c are the specific volume of the melt and crystal phases, respectively. The specific volume for each phase is taken from the literature as ν_m = 9.1× 10⁻⁷ m³/g and ν_c = 8.5 × 10⁻⁷ m³/g based on dilatometry measurements [44]. To determine the condition ξ = 1 for our measurements we perform a linear regression on the slow crystallization dynamics observed at later times and set the intersection of that linear fit and the modified Avrami fit to the crystallization data as α_∞, the crystallinity where ξ = 1. This process leads to crystallinities ranging from α_∞ = 0.34 at 40 °C to α_∞ = 0.39 at 44 °C which are converted to ϕ_∞ at each temperature using eq 3.

Many empirical models have been proposed to describe the modulus as a function of the relative semicrystalline volume fraction. These have appeared in the form of mixing rules to interpolate from the storage modulus in the melt state G_m′ to the semicrystalline state G_∞′. One of the initial mixing rules invoked a simple linear mixing rule

$$G^{\prime }=\xi {G_{\mathrm{\infty }}}^{\prime }+\left(1-\xi \right){G_{\mathrm{m}}}^{\prime }$$ (4)

based on separate measurements of the modulus (via rheometer) and crystallinity (via DSC) [5, 7]. Equation 4 is a known upper bound on the shear modulus of elastic composite materials proposed by Voigt [45, 46]. The model assumes that the strain is uniform within both components of the composite for an applied stress. If the stress is assumed uniform for a given strain then the model of Reuss is recovered [47]:

$$\frac{1}{G^{\prime }}=\frac{\xi }{{G_{\mathrm{\infty }}}^{\prime }}+\frac{1-\xi }{{G_{\mathrm{m}}}^{\prime }}.$$ (5)

This inverse mixing rule forms a lower bound on the modulus for a given volume fraction. Equations 4 and 5 have both been applied to the elastic deformation of semicrystalline solid polymers to relate the modulus to crystallinity [48]. Other groups have posited that a linear combination of the logarithm of the storage modulus will adequately relate the mechanical properties to crystallinity [12, 49]:

$$\ln G^{\prime }=\xi \ln {G_{\mathrm{\infty }}}^{\prime }+\left(1-\xi \right)\ln {G_{\mathrm{m}}}^{\prime }.$$ (6)

Although this model was proposed empirically for semicrystalline polymers [50], the logarithmic mixing rule can be derived for elastic materials with a random orientation of dispersed crystalline inclusions [51].

We compare eqs 4 – 6 with the modulus-crystallinity measurements at 44 °C in Figure 4. The linear and inverse mixing rules form a wide envelope that encompasses our experimental results, but neither function is an adequate relationship for the crystallization of PCL. The results appear to follow the logarithmic mixing rule at low crystallinities but exceed the mixing rule when ξ > 0.2.

Figure 4.

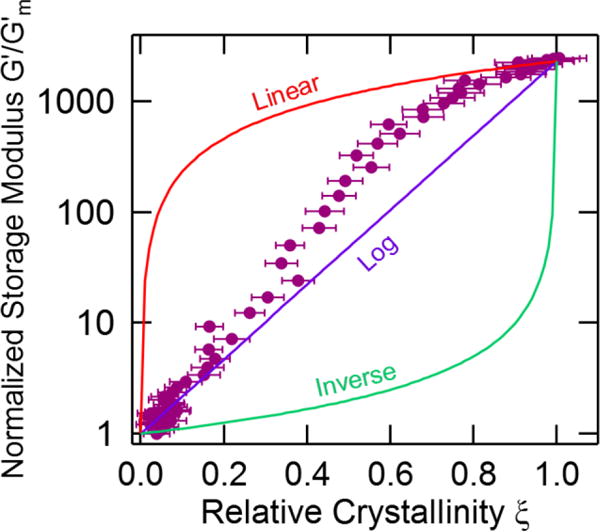
A comparison of the modulus-crystallinity data for crystallization at 44 °C with various mixing rules. Error bars indicate propagated uncertainty from the fits to the Raman spectra.

The simple mixing rules cannot adequately predict the modulus-crystallinity relationship over the crystallinity range, but we can still draw fundamental conclusions from the results. Our measurements fall within the bounds of the linear and inverse mixing formulas, which are rigorous physical bounds for composite materials. This provides further verification that the crystallinity as measured by Raman spectroscopy is an adequate measurand to characterize the extent of the crystallization process that is mechanically measured via rheology. The linear mixing rule, which has been used numerous times in the literature to estimate crystallinity, dramatically overpredicts the sensitivity of the rheological measurement to crystalline fractions. The agreement between the logarithmic mixing rule and the results at smaller crystallinities indicates that the semicrystalline domains grow without any preferred orientation, which is expected for crystallization from a quiescent melt. The deviation from the log mixing rule at larger crystallinities indicates that the structure has effectively changed from dispersed, randomly oriented crystalline structures. We expect that the increasing crystallinity will eventually lead to overlap and connectivity of the semicrystalline domains throughout the material to generate a semicrystalline solid. The mixing rules eqs 4 – 6 cannot account for this structural transition.

Composite Sphere Models

Increasing in complexity from the empirical models are composite sphere models, which relate the fraction of solids suspended in a matrix by modeling the stress-strain relationship of a single spherical particle embedded in a spherical matrix. The composite sphere model of Christensen and Lo[15, 16] has been used previously to relate the complex modulus G* to the crystallinity. The model calculates the effective shear modulus of a single particle of radius a and modulus G_∞ embedded in an elastic spherical matrix of modulus G_m and radius b. The matrix interface is coupled to an effective homogeneous material that possesses the same mechanical properties of the composite sphere-matrix system. The equation for the elastic shear modulus can be extended to viscoelastic materials via the correspondence principle [52, 53]. As a result, the model seeks a complex solution to the equation

$$A\ast \left(\xi \right){\left(\frac{G\ast }{G_{\mathrm{m}}^{\ast }}\right)}^2+B\ast \left(\xi \right)\left(\frac{G\ast }{G_{\mathrm{m}}^{\ast }}\right)+C\ast \left(\xi \right)=0$$ (7)

where the volume fraction is ξ = a³/b³. The complex coefficients A*(ξ), B*(ξ), and C*(ξ) depend on the modulus ratio $G_{\mathrm{\infty }}^{\ast }/G_m^{\ast }$ as well as the Poisson ratios of the polymer melt ν_m and the semicrystalline solid ν_∞. (The coefficients are given in the Supplementary Material.) This model has been applied to rheological measurements of crystallizing polyethylenes [18] and isotactic polypropylenes [17]. In addition to the composite sphere model, Christensen and Lo also developed a composite cylinder model for the transverse shear modulus of a fiber composite [15]. Since we are not subjecting PCL to large strains, we do not expect orientation or alignment of semicrystalline domains in a preferential direction. Also, our optical microscopy measurements confirm that the sample does not crystallize via rod-like structures at these temperatures. We therefore do not apply the composite cylinder model to our experimental results.

We can directly apply eq 7 to our polycaprolactone crystallization measurements. The measured complex modulus G* is first normalized by the initial modulus $G_m^{\ast }$, the semicrystalline modulus is chosen as $G_{\mathrm{\infty }}^{\ast }=G\ast \left({\varphi }_{\mathrm{\infty }}\right)$, and a best fit of $G\ast /G_{\mathrm{m}}^{\ast }$ is determined by varying the melt and semicrystalline Poisson ratios using a robust nonlinear regression approach with bisquare weighting [54]. Figure 5 shows the best fit of eq 7 to the crystallization measurements performed at 44 °C. The model provides a good prediction of G* at vary small relative crystallinities but deviates significantly from the real and imaginary components of the modulus over the remaining crystallinity range. The model also predicts that tan δ should remain approximately constant until δ ≈ 0.5, which does not match our measurements. The best-fit Poisson ratios indicate that both the semicrystalline solid and melt are incompressible.

Figure 5.

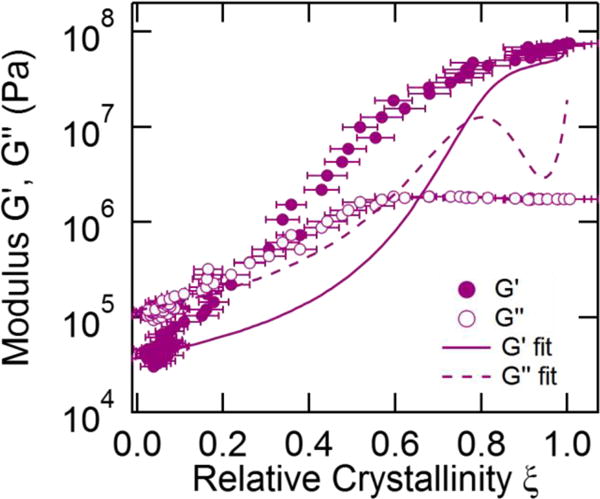
The 44 °C crystallization measurements plotted with the fits from the model of Christensen and Lo[15], eq 8. The matrix modulus $G_{\mathrm{m}}^{\ast }$ and the semicrystalline modulus $G_{\mathrm{\infty }}^{\ast }$ are fixed, but the Poisson ratios ν_m and ν_∞ are used as fitting parameters. The best fit results are at the upper bound ν_m = ν_s = 0.500. Error bars indicate propagated uncertainty from the fits to the Raman spectra.

The model of Christensen and Lo is a single description of the system that utilizes composite spheres, but there are a number of other composite sphere models that could be used to fit the crystallinity to the modulus [55]. Fitting each model to our experiments would be overly cumbersome. We can instead compare the measured modulus-crystallinity relationship to theoretical limits for composite sphere models to assess whether this type of structural model is applicable. Christensen[56] developed an upper bound for the complex shear modulus for a spherical inclusion embedded in a viscoelastic matrix based on variational methods. In the limit of hard spheres, Christensen developed upper bounds for the real and imaginary parts of the complex modulus which we can write in terms of the absolute magnitude of the modulus as

$$\frac{\left|G\ast \right|}{\left|G_{\mathrm{m}}^{\ast }\right|}\le 1+\frac{30\xi \left(1-{\nu }_{\mathrm{m}}\right)\left(7-10{\nu }_{\mathrm{m}}\right)\left({\xi }^{7/3}-1\right)}{4\left(4-5{\nu }_{\mathrm{m}}\right)\left(7-10{\nu }_{\mathrm{m}}\right)\left(1-\xi \right)\left({\xi }^{7/3}-1\right)+63\xi {\left(1-{\xi }^{2/3}\right)}^2}.$$ (8)

Figure 6 shows eq 8 compared with our isothermal crystallization measurements for a melt Poisson ratio of ν_m = 0.5. The crystallization process exceeds the upper bound developed by Christensen over a significant range of relative crystallinities for all temperatures. At higher relative crystallinities the measurements fall within the upper bound, which approaches infinity as ξ → 1.

Figure 6.

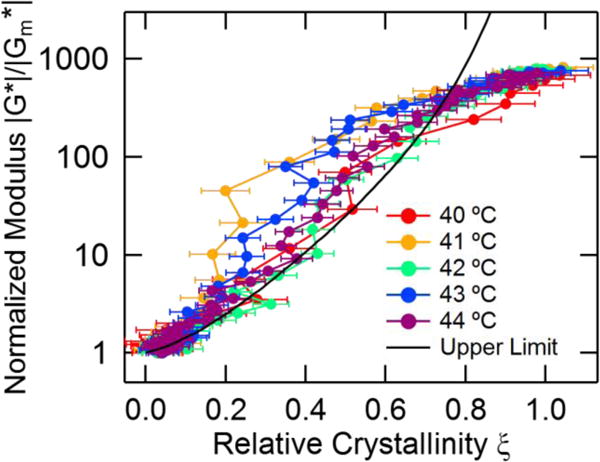
A comparison of the modulus-crystallinity data and the variational bounds for a suspension of hard spheres proposed by Christensen [56]. Error bars indicate propagated uncertainty from the fits to the Raman spectra.

The discrepancy between our results and the variational limit of eq 8 indicates that a composite sphere model is not likely to fit the polycaprolactone crystallization process. This is not entirely surprising, since our polarized microscopy measurements (see Supplementary Material) do not indicate the growth of spherical semicrystalline domains. Rather, the granular birefringent domains tend to increase in number and intensity during crystallization. As a consequence of this structure growth process the crystallinity increases the modulus much more significantly than would be expected by a suspension of hard spheres, which suggests that a simple hard-sphere inclusion model should not be used. This result is in agreement with Coppola et al. [8], who showed that the rheology of a crystallizing polypropylene is not comparable to a suspension of glass beads dispersed in a polypropylene melt.

A critical conceptual limitation of the composite sphere model can be understood by considering the growth of semicrystalline domains in a polymer melt. As the volume fraction increases, the individual semicrystalline domains will begin to impinge. The size of the semicrystalline regions will continue to increase until eventually a spanning network of semicrystalline domains form within the melt. Clearly, the composite sphere models of eqs 7 and 8 cannot capture this process of network formation. Mechanical models that include a percolation transition from a liquid suspension with solid domains to a solid composite with liquid domains would be expected to reasonably capture the rheology of the crystallization process.

Suspension Model Across the Percolation Threshold

Suspension-based models have been applied to polymer crystallization to model the effect of crystallinity on the steady shear viscosity during crystallization up to a point where network percolation occurs [4, 13, 57]. A benefit of suspension-based models is that very simple, general models can be used to predict the viscosity of suspensions over a wide range of particle shapes up to an asymptote at the percolation threshold [58–61]. Beyond the percolation threshold, the gelled suspension develops an elastic modulus that continues to increase with increasing solid fraction [62]. By using simple suspension-type models for a general particle shape, we will demonstrate that a crystallinity-modulus relationship can be developed over the crystallinity range.

The viscosity of a dispersion of particles in a viscous fluid will affect the viscosity based on particle volume fraction and the material properties of the particle. The viscosity η of a suspension at low particle volume fractions can be expanded as a power series as [59, 62]

$$\eta ={\eta }_0\left(1+\left[\eta \right]\varphi +O\left({\varphi }^2\right)\right)$$ (9)

where η₀ is the viscosity of the suspending fluid and [η] is the intrinsic viscosity of the suspension. The intrinsic viscosity is a function of the particle shape, viscosity, and flexibility [61]. At higher volume fractions, semi-empirical models for the suspension viscosity have been developed to account for the dramatic increase in viscosity when the particles approach a critical volume fraction ϕ_c. The structure at ϕ_c allows for rigidity percolation throughout the sample and is the gelation point. The critical volume fraction where gelation occurs is a function of the particle properties, temperature, and shear rate [59]. A model for the suspension viscosity developed by Krieger and Doherty [63] has been useful in characterizing the viscosity of suspensions over the accessible volume fraction range,

$$\eta ={\eta }_0{\left(1-\frac{\varphi }{{\varphi }_{\mathrm{c}}}\right)}^{-\left[\eta \right]{\varphi }_{\mathrm{c}}}.$$ (10)

This equation can be developed from mean-field arguments [62]. The intrinsic viscosity is positive for rigid particles of arbitrary shape, which means that the suspension viscosity diverges with a power law exponent of [η]ϕ_c. Maron and Pierce [64] (and later Quemada [65]) developed a similar functional form for suspensions of particles where the exponent [η]ϕ_c. = 2, and observations based on a range of experimental and theoretical measurements led Metzner [58] and Bicerano et al. [59] to conclude that an exponent of [η]ϕ_c = 2 and an appropriate value of ϕ_c in eq 10 would provide a good approximation for the viscosity of a suspension containing particles of arbitrary shape up to the gelation point.

Many authors have drawn an analogy between the hydrodynamics of fluid suspensions and the mechanics of incompressible solids with dispersed particles [60, 66, 67]. Experiments have also indicated an equivalence between the relative viscosity η/η₀ of hard spheres dispersed in a fluid and the relative elastic modulus G/G₀ of the same particles dispersed in a solid matrix with modulus G₀ [60, 67]. Given this information, we will assume that the shear modulus of a suspension will follow a model similar to the Krieger-Dougherty equation,

$$G=G_0{\left(1-\frac{\varphi }{{\varphi }_{\mathrm{c}}}\right)}^{-\left[G\right]{\varphi }_{\mathrm{c}}}$$ (11)

where [G] is the intrinsic shear modulus. Similar to [η], the value of [G] is a function of the shape, shear modulus, and deformability of the dispersed phase [59, 68]. For deformable elastic particles of initial spherical shape, the intrinsic modulus is a function of the particle modulus G_p and the matrix modulus as

$$\left[G\right]=\frac{\frac{G_{\mathrm{p}}}{G_0}-1}{1+\frac{2}{5}\left(\frac{G_{\mathrm{p}}}{G_0}-1\right)}.$$ (12)

When the particle has a larger modulus than the matrix G_p > G₀ the intrinsic modulus is positive and eq 11 predicts a power law increase in the modulus, with a limiting value of [G] = 2.5 at infinite particle modulus. However, dispersions of soft particles in a high modulus matrix G₀ > G_p result in a negative intrinsic modulus and a corresponding decrease in the composite shear modulus with increasing particle volume fraction.

The elastic version of the Krieger-Dougherty equation (eq 11) will be used to develop a model across the percolation transition, based on two ideal cases. In Case I, an elastic material of modulus G₀ is filled with dispersed rigid particles. The effective shear modulus will diverge as the percolation threshold is approached from below with a power law exponent s

$$G_{\mathrm{I}}=G_0{\left(1-\frac{\varphi }{{\varphi }_{\mathrm{c}}}\right)}^{-s}$$ (13)

where we have generalized the Krieger-Dougherty exponent [G]ϕ_c = s > 0. Case II is an elastic material with modulus G₁ where a volume fraction (1 − ϕ) of deformable voids are added and the solid volume fraction ϕ decreases. The resulting effective modulus will be of a similar form to eq 11 with a negative intrinsic shear modulus as we approach the critical percolation threshold

$$G_{\text{II}}=G_1{\left(\frac{\varphi -{\varphi }_{\mathrm{c}}}{1-{\varphi }_{\mathrm{c}}}\right)}^t$$ (14)

with a scaling exponent t > 0. This model is similar to equations for the Young’s modulus of porous elastic materials over a wide range of microstructure [69]. Equations 13 and 14 describe idealized cases that have an asymptote in G_I and ln G_II at the critical percolation fraction.

If we had an intermediate case where particles of modulus G₁ were added to a matrix of modulus G₀ and G₀ ≪ G₁, we would expect the effective modulus to follow the scaling of eq 13 for ϕ < ϕ_c and the scaling of eq 14 when ϕ > ϕ_c. Equations of a similar form are encountered in theories of the electrical conductivity of composites, and to address the issue of the asymptote at the critical threshold (for electrical percolation) a general effective medium equation has been proposed that interpolates across the percolation threshold [70]. We can construct a general effective medium equation for the elastic shear stress of such a material

$$\left(1-\varphi \right)\frac{G_0^{1/s}-G^{1/s}}{G_0^{1/s}+A_{\mathrm{p}}{G}^{1/s}}+\varphi \frac{G_1^{1/t}-G^{1/t}}{G_1^{1/t}+A_{\mathrm{p}}{G}^{1/t}}=0$$ (15)

where A_p = (1−ϕ_c)/ϕ_c. This equation is proposed as a formula for the effective elastic modulus G as a function of ϕ. In the limit of G₁ → ∞, the general effective medium equation yields the scaling of eq 13, and the limit as G₀ → 0 yields eq 14. The shape of the modulus-crystallinity curve predicted by eq 15 is strongly dependent on the magnitude difference between the matrix modulus G₀ and the particle modulus G₁ as well as the fitting parameters ϕ_c, s, and t. Figure 7 shows examples of the general effective medium equation for various parameter values. Figure 7a shows that with increasing particle hardness (larger G₁), the modulus-volume fraction curve appears more sigmoidal. Figure 7b demonstrates that that critical percolation fraction sets the inflection point in the sigmoidal curve for a single exponent q, and the exponent determines the sensitivity of the modulus to changes in the volume fraction near the critical percolation fraction (Figure 7c). Conditions where q is large approximate the logarithmic mixing rule eq 6. Conditions where the exponents s and t are not equal will generate more complicated modulus-volume fraction relationships as shown in the Supplementary Material. We note that the elastic moduli in eq 15 can be replaced with complex viscoelastic moduli through the use of the correspondence principle [52, 53]. For frequency-dependent conditions, the complex moduli $G_0^{\ast }$ and $G_1^{\ast }$ should be measured at the same oscillation frequency.

Figure 7.

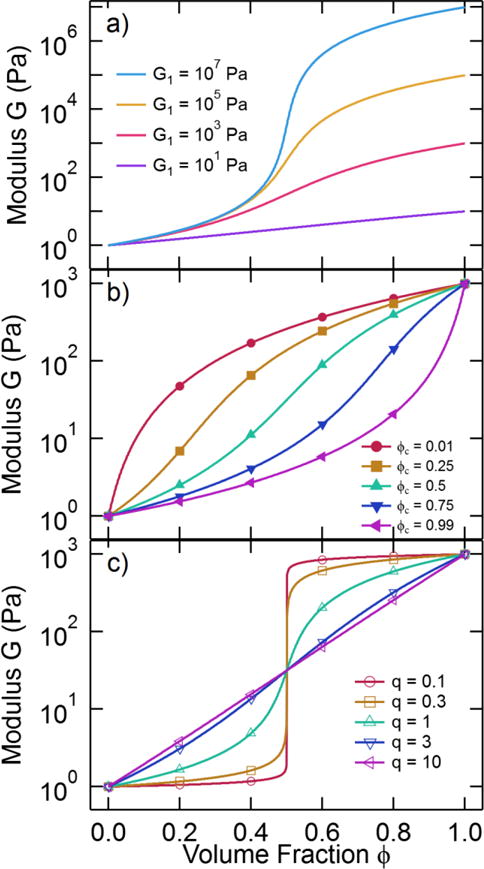
The generalized effective medium equation (eq 15) for G₀ = 1 Pa and different values of G₁, ϕ_c, and a single exponent q: a) varying G₁ for ϕ_c = 0.5 and q = 2, b) varying ϕ_c for the condition q = 2 and G₁ = 1000 Pa, and c varying q for ϕ_c = 0.5 and G₁ = 1000 Pa.

We can apply the general effective medium equation with viscoelastic moduli to our crystallization data by making two simplifying assumptions. Our first assumption is that we can replace the absolute volume fraction ϕ with the relative volume fraction of semicrystalline material ξ. The relative volume fraction is the relevant parameter for crystallizing polymers since the high modulus particles growing from the melt are not entirely crystalline, but a combination of crystalline lamellae separated by amorphous domains. This implies that the suspended particles have the same modulus as the semicrystalline polymer at ξ = 1; we therefore replace the value of $G_1^{\ast }$ with $G_0^{\ast }$. We will also assume that the exponents are equal (s = t = q) to obtain a general effective medium equation to relate crystallinity and the complex modulus across a percolation threshold at a critical relative crystallinity ξ_c,

$$\left(1-\xi \right)\frac{{\left(G_{\mathrm{m}}^{\ast }\right)}^{1/q}-{\left(G\ast \right)}^{1/q}}{{\left(G_{\mathrm{m}}^{\ast }\right)}^{1/q}+A{\left(G\ast \right)}^{1/q}}+\xi \frac{{\left(G_{\mathrm{\infty }}^{\ast }\right)}^{1/q}-{\left(G\ast \right)}^{1/q}}{{\left(G_{\mathrm{\infty }}^{\ast }\right)}^{1/q}+A{\left(G\ast \right)}^{1/q}}=0,$$ (16)

where A = (1 − ξ_c)/ξ_c. We fit eq 16 to the complex modulus by finding the best fit real values of A and the exponent q. The results in Figure 8 show that the model provides an acceptable fit to both the storage and loss moduli over the entire crystallization process (see Supplementary Material for fit results to other temperatures). Attempts to fit two separate exponents s and t yield an improved fit to the experimental results, however the uncertainty in the fitting parameters is large and so a three-parameter fit is not pursued here. We provide the average values of q and ξ_c based on measurements of three samples in Figure 9.

Figure 8.

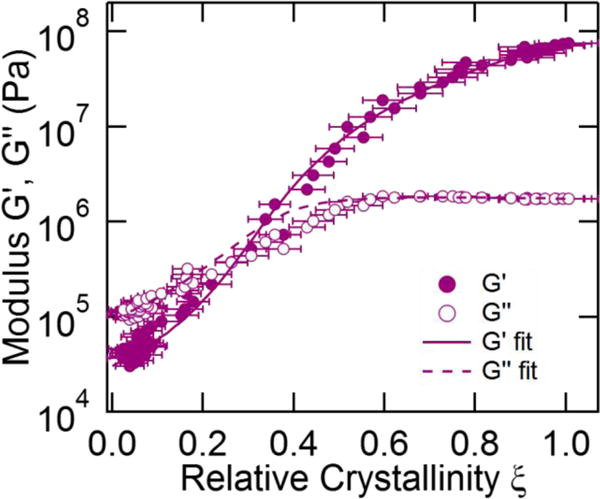
Modulus versus crystallinity at 44 °C fit to eq 16. The coefficients are ξ_c = 0.36 ± 0.01, q = 1.78 ± 0.11. Error bars indicate propagated uncertainty from the fits to the Raman spectra.

Figure 9.

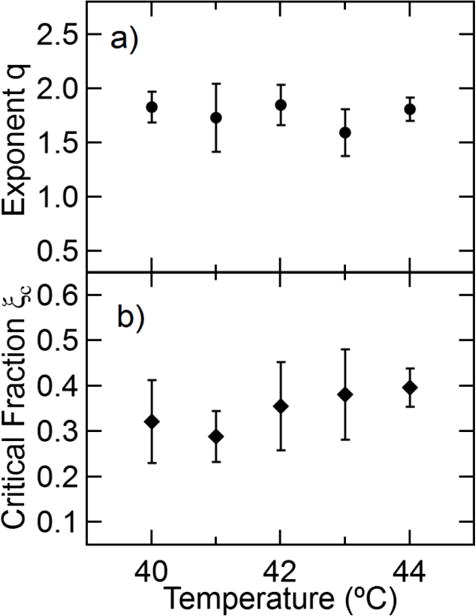
a) Scaling exponent q for the different isothermal crystallization temperatures and b) critical fraction. Error bars are the standard deviation of measurements on three different samples.

The exponent q remains approximately constant over the narrow isothermal crystallization temperature range studied (Figure 9a). The lack of a temperature dependence indicates that the crystallization process proceeds through a similar average structure which we attribute to the narrow range of temperatures probed in this work. The measured values of the exponent are approximately 1.8, which is near the expected exponent of 2 for a suspension of arbitrary-shape particles in viscous liquids [58, 59] or polymer melts at low shear rates [71]. Our measurements are also well within the range of exponents (1.64 < t < 2.30 in eq 14) calculated for the linear elastic properties of porous solids with varying pore shapes [69]. This agreement indicates that the shear modulus above the percolation transition is dominated by the modulus of the semicrystalline domains with negligible contribution from the remaining melt fraction.

The critical percolation fraction ξ_c is also largely independent of temperature as shown in Figure 9b, however we note a slight increase in ξ_c with increasing temperature. The percolation transition occurs in the approximate range of 0.3 to 0.4, which is equivalent to mass fraction crystallinities in in the range of 0.09 < α_c < 0.16. This mass fraction increases with temperature, which indicates that more crystallinity is needed for stress transfer across the crystallizing polymer at higher temperatures. Comparing these results with Figure 3 indicates that the critical percolation fraction is approximately equal to the crystallinity where tan δ = 1 (at ω = 2π rad/s) during crystallization. This suggests that the formation of a spanning structural network coincides with the mechanical transition from liquid-like to solid-like. We note that the occurrence of this mechanical transition at tan δ = 1 is largely coincidental, since prior measurements of a larger molar mass PCL indicate that the liquid-to-solid transition determined from the gelation point does not occur at tan δ = 1 [22]. Information on the shape of the suspended semicrystalline material is encoded in the critical relative volume fraction ξ_c. The critical percolation fractions in our measurements are well below the value of 0.64 expected in the random close packing limit of monodisperse hard spheres [62]. Values below the random close packing limit indicate that the semicrystalline domains are growing with a non-spherical shape, however the approximate shape cannot be determined by ξ_c alone. Theoretical calculations indicate that suspensions of rods [72], platelets [59], or fractal aggregates will have critical percolation fractions in the range of 0.3 – 0.4. We also note that these calculations assume monodisperse structures in a suspension, which is clearly not observed in our optical images (Figure S3 of the Supplementary Material).

The relationship between s, ϕ_c, and [G] in eq 13 suggests that we should also be able to write an intrinsic parameter based on q and ξ_c from eq 16. We therefore define [G*] = q/ξ_c as an intrinsic modulus that describes the increase in the modulus due to small additions of crystalline material, which we can compare with the intrinsic viscosity of solid particles. For the crystallization measurement shown in Figure 8, [G*] = 4.95 ± 0.50. This is well beyond the upper limit of the intrinsic shear modulus of elastic materials predicted by eq 12 for spherical particles, which further indicates the growth of non-spherical structures. Raman-based measurements of crystallinity are limited to relative volume fractions ξ > 0.04 which is near the limit where higher-order terms should be included in the expansion (eq 9). For non-spherical particles, the deviation from the linear relationship occurs at even smaller volume fractions.

In comparison to the suspension-percolation model developed here, the rheology of the crystallization process has been suggested to proceed via physical gelation. In the physical gelation process, crosslinks are formed due to intermolecular associations that generate a network structure [73]. Evidence of this physical crosslinking was shown in the work of Pogodina and Winter on crystallizing isotactic polypropylenes [19] – at the gelation point, a frequency range of the relaxation spectrum exhibits power law dynamics. These dynamics are indicated by a frequency-independent tan δ, which has been observed previously in the isothermal crystallization of polycaprolactone [22]. Gelation models were previously used to analyze crystallizing polyolefins above the critical point [21] by using an empirical crystallinity-modulus relationship developed by Takayanagi et al. [74].

Physical gelation processes are characterized by a viscosity and elastic modulus that exhibit a power law dependence on ε = |p − p_c|, where p is the extent of reaction and p_c is the gel point. Given the functional similarities between the scaling for the viscosity and shear modulus in gelation processes [75] and the power law scaling with volume fraction shown in eqs 10 and 14, an argument could be made for analyzing our modulus-crystallization measurements using gelation theory (assuming ε = |ξ − ξ_c|). We can compare the well-known scaling exponents for gelation processes [75] to our measured scaling exponent q. Our scaling exponent falls well below the values of the exponent for the elastic modulus predicted by classical mean field theory (t = 3) or Rouse-Zimm theory (t = 2.7) but is closer to the exponent predicted by electrical network theory (t = 1.94) [75]. Gelation theories for the viscosity below the percolation transition have exponents in the range of 0 to 1.35, which falls well below our average q. Based on these comparisons, we find that a suspension-based model applied across the percolation threshold provides a better explanation for the evolution of mechanical properties during polycaprolactone crystallization.

We note that the general effective medium equation can have up to three fitting parameters, which either requires a significant number of experimental points along the modulus-crystallinity curve or an independent measurement of multiple parameters to simplify the fitting process. Fitting too few data points can result in large uncertainty in the fitting parameters; for example, attempts to apply the general effective medium model to previously published modulus-crystallinity measurements performed on a rheo-DSC instrument [18] exhibit large uncertainty in the fitting parameters due to a small number of data points between the melt state and the final semicrystalline state.

Although our measurements are performed at a single arbitrary frequency, the frequency dependence of the modulus during the crystallization process merits further study using this suspension-based analysis. A superposition of angular frequencies can be used to probe the evolution of the relaxation dynamics during the crystallization process [76]. Given the wide variety of crystallinity-modulus curves that can be generated with our model (Figure 7), we expect that the general effective medium equation can be applied over a broad frequency range if the fitting parameters q and ξ_c are assumed frequency-dependent. Frequency sweeps at various stages of the crystallization process would allow us to not only determine the frequency dependence of these parameters but also determine whether these parameters can be explained in context of the gelation model for polymer crystallization [19]. We note that the “inverse quenching” technique of Acierno and Grizzuti [77] can be utilized to slow down the crystallization process to probe a wider frequency range at different crystallinities.

We expect that our measurement technique of combined rheology and Raman spectroscopy will work best in polymer samples that exhibit smaller crystalline domains similar to the birefringent granules that we have reported for PCL in our optical microscopy measurements. With these smaller structures, the laser scattering volume is more likely to contain an average of semicrystalline domains and amorphous melt domains. Polymers that crystallize via the growth of large spherulites, such as isotactic polypropylene [14, 19], might only occasionally grow spherulitic structures within the sampling volume of the laser. One potential solution is to perform a series of crystallinity measurements across the radius of the sample during the crystallization process, which would not only average the crystalline and melt domains but also indicate the spatial variation in crystallinity within the sample on the rheometer. This is outside the scope of the current manuscript.

The success in fitting the general effective medium equation to both real and imaginary parts of the complex modulus indicates that the rheological response of PCL crystallization can be explained via suspension-type models across the percolation threshold. Also, we have shown acceptable fits to the data with a single exponent q on both sides of ξ_c, although the scaling exponents above and below the percolation transition need not be so restricted.

Conclusions

Simultaneous measurements of rheology and crystallinity during the isothermal crystallization of polycaprolactone allow us to directly probe the relationship between structure and mechanics. The modulus-crystallinity relationship can be used as a critical probe of the various models used to relate these two properties. Our measurements reveal that neither rheology nor birefringence should be used as the sole quantitative indicator of crystallinity during the crystallization process. We find that neither empirically-derived mixing rules nor composite sphere models like those of Christensen and Lo [15] can adequately describe the crystallization results, however a suspension-type model applied across the percolation threshold is shown to fit the results remarkably well.

By analyzing the modulus-crystallinity data using our suspension model, we find that a critical percolation fraction and a single scaling exponent above and below the percolation threshold are sufficient to fit the data. Our results further the idea that the mechanics of polymer crystallization can be described using suspension-type models, and further theoretical and experimental work is required to determine the relationship between the fit parameters and molecular or crystal structure parameters. As it stands, the parameters from the general effective medium model should be used as empirical parameters that characterize the rheological response of crystallizing polymers. We further expect that this model will be beneficial in characterizing the effect of flow and nanoparticle additives on the crystallization process.