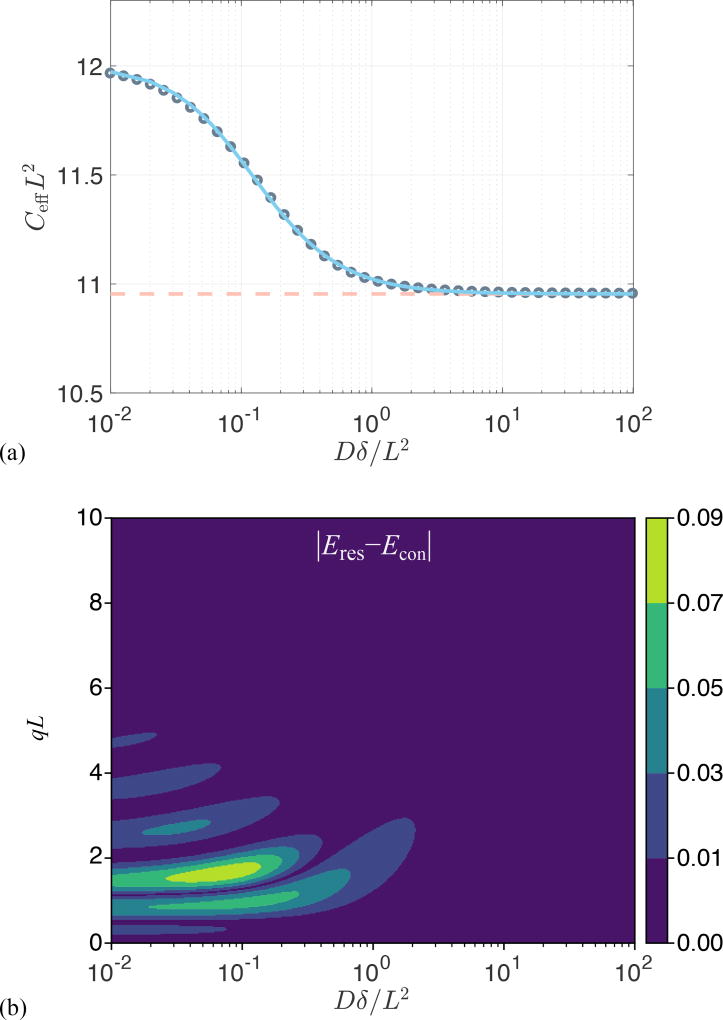
Figure 1.

(a) Effective dimensionless confinement value (gray circles) computed by matching the variances of the center of mass distributions in the two problems plotted vs. the dimensionless time Dδ/L². The variation in C_effL² value is well-captured (error less than 0.12%) by the expression $y=12-(12-\sqrt{120}){(\alpha x)}^{c\gamma }{[1+{(\alpha x)}^c]}^{-\gamma }$, with α = 9.495, γ = 1.210, and c = 1.266 (blue line). The dashed line indicates the asymptotic value $\sqrt{120}$. (b) The absolute value of the difference in the normalized signals implied by the two problems (restricted diffusion with separation L, and the Hookean potential with a confinement value taken to be $C=\sqrt{120}{L}^{-2}$) for a traditional Stejskal-Tanner sequence [32] with two gradient pulses whose leading edges are separated by Δ with DΔ/L² = 100. The restricted diffusion signal was computed using the multiple correlation function method [33, 34].