Frictional lubricity enhanced by quantum mechanics

Significance

Sliding friction, a corner of physics still under debate after centuries, is currently studied in nanosystems such as optical lattice emulators, where parameters are easy to control but where applicability of classical mechanics is no longer guaranteed. The quantum effects on friction being largely unexplored, we show here that even a basic theoretical model predicts important novelties. For a particle dragged over large barriers, whose classical stick–slip friction would be large, Landau–Zener tunneling through the barrier can avert stick–slip, with an increase of lubricity. This and related forms of quantum lubricity should be observable for cold ions sliding in optical lattices.

Abstract

The quantum motion of nuclei, generally ignored in the physics of sliding friction, can affect in an important manner the frictional dissipation of a light particle forced to slide in an optical lattice. The density matrix-calculated evolution of the quantum version of the basic Prandtl–Tomlinson model, describing the dragging by an external force of a point particle in a periodic potential, shows that purely classical friction predictions can be very wrong. The strongest quantum effect occurs not for weak but for strong periodic potentials, where barriers are high but energy levels in each well are discrete, and resonant Rabi or Landau–Zener tunneling to states in the nearest well can preempt classical stick–slip with nonnegligible efficiency, depending on the forcing speed. The resulting permeation of otherwise unsurmountable barriers is predicted to cause quantum lubricity, a phenomenon which we expect should be observable in the recently implemented sliding cold ion experiments.

Friction is, among all basic physical phenomena, the one in most need of fundamental work. In particular, the main current understanding of friction, largely based on mesoscale and nanoscale developments, is essentially classical (1). Quantum effects in sliding friction, despite some early and laudable work (2–4) including experimental suggestions (5), have not been discussed very thoroughly so far. In most cases, in fact, the forced motion of atoms, molecules, and solids is considered, and simulated, just classically. The quantum effects that may arise at low temperatures, connected with either quantum freezing of the phonons or a slight quantum smearing of classical energy barriers, are not generally deemed to be dramatic and have received very little attention. At the theoretical level, in particular, quantum frictional phenomena were not pursued after and beyond those described by the seminal path-integral Monte Carlo study in the commensurate Frenkel–Kontorova model (2, 3). Possible reasons for this neglect are the scarcity of well-defined experimental frictional realizations where quantum effects might dominate and, symmetrically, on the theory side, the lack of easily implementable quantum dynamical simulation approaches. Cold ions in optical lattices (6) offer brand new opportunities to explore the physics of sliding friction, including quantum aspects. Already at the classical level, and following theoretical suggestions (7), recent experimental work on cold ion chains demonstrated important phenomena such as thermolubricity (8), the Aubry transition (9–11), and multiple frictional slips (12). The tunability of the perfectly periodic optical potential that controls the motion of atoms or ions should make it possible to access regimes where quantum frictional effects can emerge.

Here we show, hopefully anticipating experiment, that a first, massive quantum effect will appear already in the simplest sliding problem, that of a single particle forced by a spring to move in a periodic potential: a quantum version of the renowned Prandtl–Tomlison model, and a prototypical system that should also be realizable experimentally by a cold ion dragged by a time-dependent confining potential. As we will show, the main quantum effect amounts to a force-induced Landau–Zener (LZ) tunneling, of course well-known and studied in many different contexts (13–16) outside of sliding friction. The effect of LZ tunneling on friction is striking because it shows up preferentially for strong optical potentials and high barriers, where classical friction is large, while resonant tunneling between levels in nearby potential wells can cause it to drop—a phenomenon that we may refer to as quantum lubricity.

Model and Methods

Our model, sketched in Fig. 1, consists of a single quantum particle of mass $M$ in the one-dimensional periodic potential created, for instance, by an optical lattice, of strength $U_0$ and lattice spacing $a$. The particle is set into motion by the dragging action of a confining potential—specifically, we will assume an harmonic potential of spring constant $k$—which moves with constant velocity $v$, representing for instance an optical tweezer or any other dragging mechanism, such as a moving Paul trap or an electric field, in the case of an ion:

$${\widehat{H}}_{\text{Q}}(t)=\frac{{\widehat{p}}^2}{2M}+U{}_0\sin ^2\left(\frac{\pi }{a}\widehat{x}\right)+\frac{k}{2}{\left(\widehat{x}-vt\right)}^2.$$ [1]

The forced motion gives the particle an energy that is removed, in the frictional steady state, through dissipation by a thermostat. As in the pioneering approach by Feynman and Vernon (17), dissipation is introduced by means of a harmonic bath (18)

$${\widehat{H}}_{\text{int}}=\sum _i\left(\frac{{\widehat{p}}_i^2}{2m_i}+\frac{1}{2}{m}_i{\omega }_i^2{\left({\widehat{x}}_i-\frac{c_i}{m_i{\omega }_i^2}\widehat{X}\right)}^2\right),$$ [2]

where each oscillator ${\widehat{x}}_i$ couples, through an interaction coefficient $c_i$, to the “periodic position” of the particle $\widehat{X}=\sin \left(\frac{2\pi }{a}\widehat{x}\right)$. Seemingly complicated, this choice of coupling is most natural, for it respects the periodicity of the substrate while still behaving linearly close to the bottom of the potential—where the particle resides with the highest probability—effectively coupling successive levels within each minimum. The coefficients $c_i$ determine the coupling strength of the bath, through the spectral function $J(\omega )=\mathrm{\hslash }{\sum }_i\frac{c_i^2}{2m_i{\omega }_i}\delta (\omega -{\omega }_i)$, which we choose of the standard Caldeira–Leggett (19) ohmic form $J(\omega )=2\alpha {\mathrm{\hslash }}^2\omega e^{-\omega /{\omega }_c}$, where ${\omega }_c$ sets the high-energy cutoff. Our simulation scheme, described below, will be exact for weak coupling only, but so long as $\alpha \ll 1$, which is well below any possible Caldeira–Leggett dissipative localization transition (19), we expect its qualitative validity to extend into the moderate coupling regime.

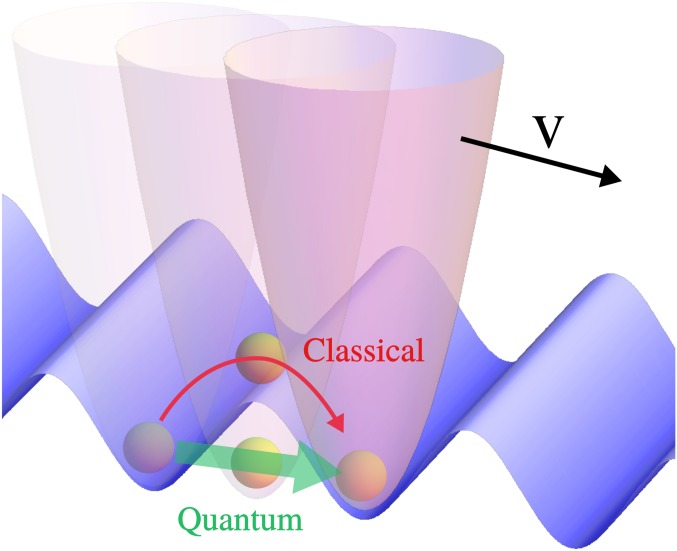
Fig. 1.

A sketch of the model: A particle dragged by a confining potential (pink) moving at velocity $v$ over a periodic potential (blue), provided for instance by an optical lattice. The two arrows allude to the classical overcoming of the barrier (red) as opposed to a quantum tunneling event (green).

We can understand the basic mechanism leading to quantum frictional dissipation by considering the instantaneous eigenstates of ${\widehat{H}}_{\text{Q}}(t)$, shown in Fig. 2A for a reduced Hilbert space with four states per well. Denoted by $\mathrm{T}=a/v$, the time period in which the driving spring moves by one lattice spacing, at $t=0$, when the harmonic potential is centered at $x=0$, the lowest eigenstate is essentially coincident with the lowest Wannier state in the $x=0$ potential well. As the harmonic spring moves forward, at $t=t_1=\mathrm{T}/2$, the particle negotiates the perfect double-well state between $x=0$ and $x=a$, where all pairs of left and right levels anticross. The LZ “diabatic” transition rate (population of the excited state after the anticrossing) between levels E_n(t) and $E_n\prime (t)$ is

$$P_{n\to n\prime }=e^{-\frac{\pi {\mathrm{\Delta }}_{nn\prime }^2}{2\mathrm{\hslash }v{\alpha }_{nn\prime }}}=e^{-\frac{v_{n\to n\prime }}{v}}$$ [3]

where ${\alpha }_{nn\prime }$ is the relative slope of the two eigenvalues involved, E_n and $E_n\prime$; ${\mathrm{\Delta }}_{nn\prime }$ their anticrossing gap; and $v$ the speed.

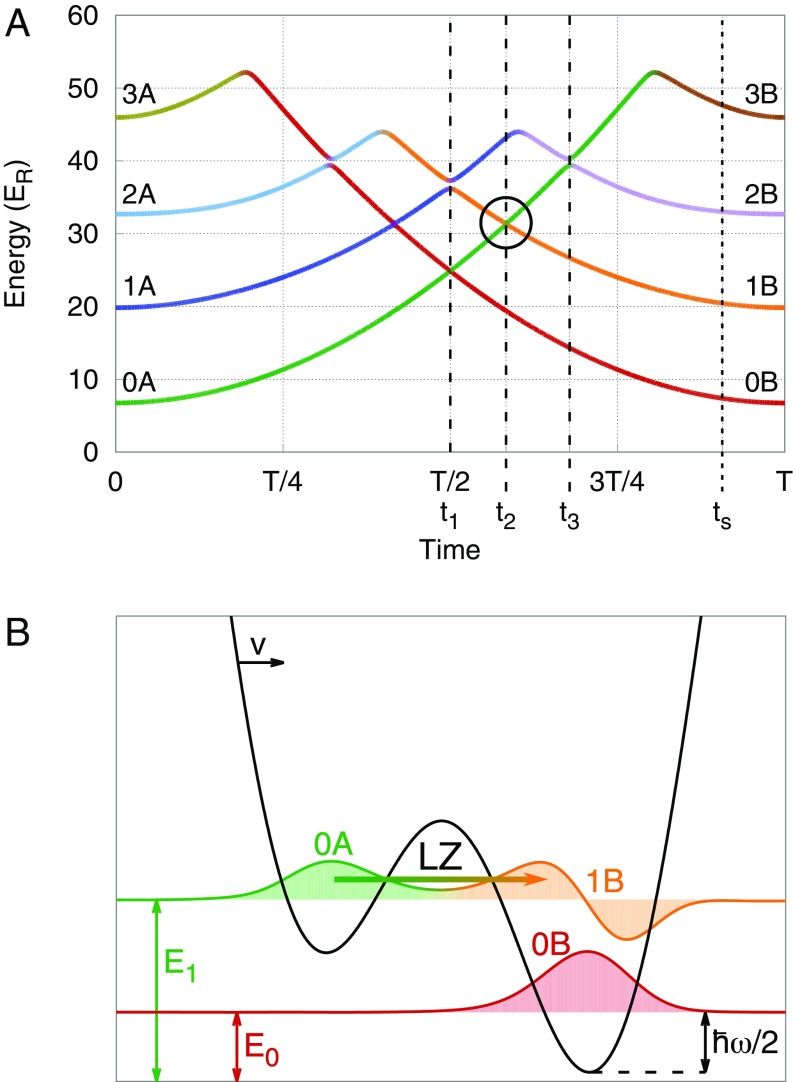
Fig. 2.

Illustrating how level quantization and Landau–Zener (LZ) tunneling affect forced barrier crossing. (A) The four lowest instantaneous eigenvalues of a particle that is adiabatically driven by the harmonic trap from a periodic potential minimum to the nearest one. All avoided crossing gaps associated with LZ tunneling events encountered during the dynamics at times $t_1$, $t_2$, and $t_3$ are nonzero, even if invisible for $t_1$ and $t_2$ on this scale. The circle highlights the resonant tunneling described in text and represented in B. (B) A pictorial sketch of the tunneling event in which a particle in the ground level of the left well (0A) resonantly tunnels into the first excited level of the right well (1B).

At the anticrossing at $t_1=\mathrm{T}/2$ between ground states at $x=0$ and $x=a$, due to the large barrier, the states are very localized and the gap, here ${\mathrm{\Delta }}_{01}$, is exceedingly small. For very small velocity, $v\ll v_{0\to 1}=\pi {\mathrm{\Delta }}_{01}^2/[2\mathrm{\hslash }{\partial }_x|(E_1-E_0)|)$, the LZ transition rate $P_{0\to 1}$ (Eq. 3), which as we shall see is proportional to the frictional dissipation, is negligible. In that low-velocity case, a quantum particle is transmitted adiabatically without friction. This is therefore a regime, which one might designate of quantum superlubricity, where friction may vanish nonanalytically as in Eq. 3 in the limit of zero speed (see Inset in Fig. 3)—totally unlike the classical case, where friction vanishes linearly with $v$ (viscous friction). Quantum superlubricity should be realized at sufficiently low temperatures, only thermally destroyed in favor of viscous lubricity as soon as temperature $T$ is large enough to upset the LZ physics behind the mechanism. This, however, is not expected to occur until $T$ becomes considerably larger than the tunneling gap ${\mathrm{\Delta }}_{01}$, as a recent study on the dissipative LZ problem has confirmed (20).

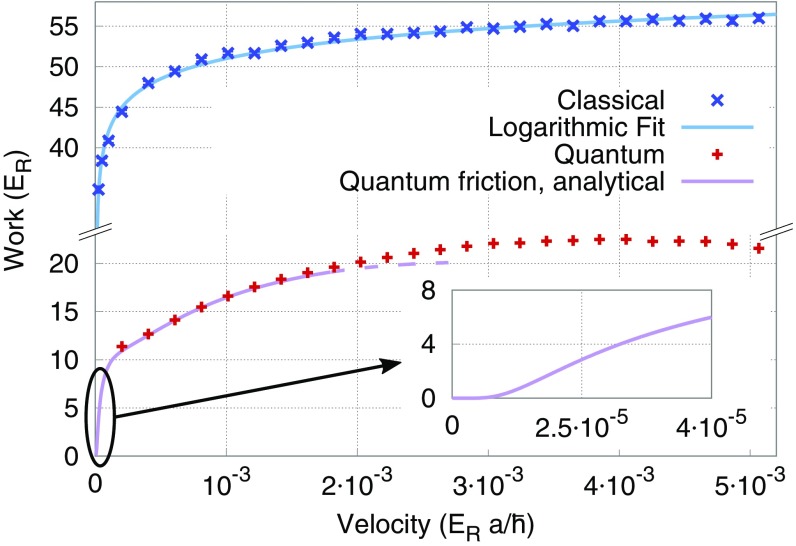
Fig. 3.

Frictional dissipation rate for classical (blue) and quantum (red) sliding vs. driving velocity. Note the large reduction of dissipation induced by the resonant quantum tunneling: quantum lubricity. Parameters are identical to those of Fig. 4. The linear friction expected in the classical case for $v\to 0$ is not visible in this scale. The quantum friction decline at high velocity is caused by insufficient cooling rate ${\gamma }_c$. (Inset) Magnified low-velocity behavior, showing the nonanalytic vanishing of friction due to $0A-0B$ tunneling (quantum superlubricity).

Moving on to larger speeds $v\gg v_{0\to 1}$, the particle, unable to negotiate the $0A\to 0B$ tunneling adiabatically, remains diabatically trapped with large probability $P_{0\to 1}$ in the lowest $0A$ Wannier state even for $t>\mathrm{T}/2$. In that regime, only at a later time, $t=t_2$, does the rising level become resonant with the first excited state 1B of the $x=a$ well. As this second gap ${\mathrm{\Delta }}_{12}$ is now much larger than ${\mathrm{\Delta }}_{01}$, the LZ diabatic rate drops and the particle transfers with large adiabatic probability from the $A$ to the $B$ well for driving speeds $v_{0\to 1}\ll v\ll v_{1\to 2}$. Once the first excited $1B$ state in the $x=a$ well is occupied, the bath can exponentially suck out the excess energy, now thermalizing the particle to the lowest $0B$ level. That sequence of events thus dissipates energy, by an amount that is paid for by frictional work done by the external force. The $0A\to 1B$ quantum slip between neighboring wells thus preempts by far the classical slip, which would take place when the rising classical minimum disappears, at $t_s=(\pi U_0/kva)\sqrt{1-{(k{a}^2/2{\pi }^2{U}_0)}^2}+(a/2\pi v){\cos }^{-1}(-k{a}^2/2{\pi }^2{U}_0)>t_2$.

To calculate the quantum frictional dissipation rate, we describe the particle motion by means of a weak coupling Born–Markov quantum master equation (QME), based on a time-evolving density matrix ${\widehat{\rho }}_Q(t)$ (20, 21), whose equation of motion is

$$\frac{d}{dt}{\widehat{\rho }}_Q(t)=\frac{1}{i\mathrm{\hslash }}[{\widehat{H}}_X(t),{\widehat{\rho }}_Q(t)]-\left([\widehat{X},\widehat{S}(t){\widehat{\rho }}_Q(t)]+\text{H.c.}\right),$$ [4]

where ${\widehat{H}}_X(t)={\widehat{H}}_Q(t)+2\mathrm{\hslash }\alpha {\omega }_c{\widehat{X}}^2$. The operator $\widehat{S}(t)$, which is in principle (21) a bath-convoluted $\widehat{X}$ given by $\widehat{S}(t)=\frac{1}{{\mathrm{\hslash }}^2}{\int }_0^{t}d\tau C(\tau ){\widehat{U}}_X(t,t-\tau )\widehat{X}{\widehat{U}}_X^{†}(t,t-\tau )$, will be approximated, on the basis of the instantaneous eigenstates $|{\psi }_k(t)⟩$ of the system Hamiltonian ${\widehat{H}}_X(t)$, as $\widehat{S}(t)={\sum }_{k,k\prime }{S}_{k,k\prime }(t)|{\psi }_k(t)⟩⟨{\psi }_k\prime (t)|$ with

$$S_{k,k\prime }(t)\approx \frac{1}{{\mathrm{\hslash }}^2}⟨{\psi }_k(t)\left|\widehat{X}\right|{\psi }_k\prime (t)⟩\mathrm{\Gamma }(E_k\prime (t)-E_k(t)),$$ [5]

where $\mathrm{\Gamma }(E^{+})\equiv {\int }_0^{+\mathrm{\infty }}d\tau C(\tau )e^{i\left(E+i{0}^{+}\right)\tau /\mathrm{\hslash }}$ is the rate for a bath-induced transition at energy $E$ and $E_k(t)$ is the instantaneous eigenvalue associated with $|{\psi }_k(t)⟩$. Here the correlator $C(\tau )\equiv {\int }_0^{+\mathrm{\infty }}d\omega J(\omega )[e^{i\omega \tau }{f}_B(\omega )+e^{-i\omega \tau }[f_B(\omega )+1]]$ contains the bath temperature $T$ through the Bose–Einstein distribution $f_B(\omega )$. Recent work on the dissipative LZ problem (20) has shown that this approximation is quite safe, when the coupling to the bath is weak, in an extended regime of driving velocities $v$ and temperature $T$. The QME is then solved on the basis of the Wannier orbitals of the unperturbed particle in the periodic potential.

Results

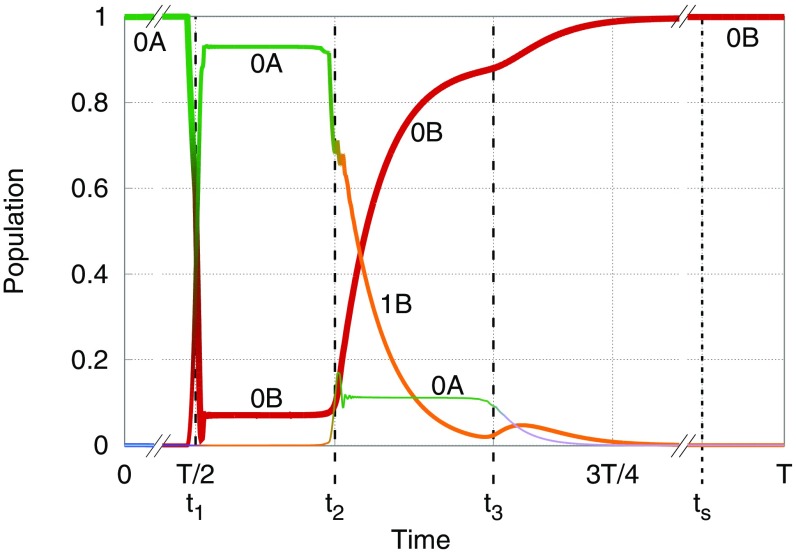
Fig. 4 shows, for an arbitrary but convenient choice of parameters, the time-dependent population probability of the first three instantaneous eigenstates, $P_k(t)=⟨{\psi }_k(t)|{\widehat{\rho }}_Q|{\psi }_k(t)⟩$, over one period of forced particle motion in the $v_{0\to 1}\ll v\ll v_{1\to 2}$ regime. As qualitatively sketched, despite the slow motion, the probability of the $0A\to 0B$ adiabatic transition to the right well ground state at $t_1=\mathrm{T}/2$ is already very small, and LZ dominates this first level crossing keeping diabatically the particle in the left $A$ well. At the second $1\to 2$ crossing, where the gap ${\mathrm{\Delta }}_{12}$ is much larger, $P_{1\to 2}$ is suppressed, and the $1^{\text{st}}$ excited level of the right well ($1B$) becomes strongly populated. Following that, the bath exponentially relaxes $P_k(t)$ down to the right well ground state.

Fig. 4.

Time-dependent population of instantaneous eigenstates 0A (green), 0B (red), and 1B (orange) for $v=4\cdot {10}^{-4}{E}_{R}a/\mathrm{\hslash }$, $U_0=38.5E_R$, $k=190E_R/a^2$, where $E_R=\pi {}^2\mathrm{\hslash }^2/(2M{a}^2)$ is the recoil energy, corresponding to the double-well potential configuration sketched in Fig. 2B. Lines of decreasing thickness are used for higher eigenstates. The ohmic coupling strength is here $\alpha =0.002$, with a cutoff ${\omega }_c=12E_R/\mathrm{\hslash }$ and temperature $T=1E_R/k_B$.

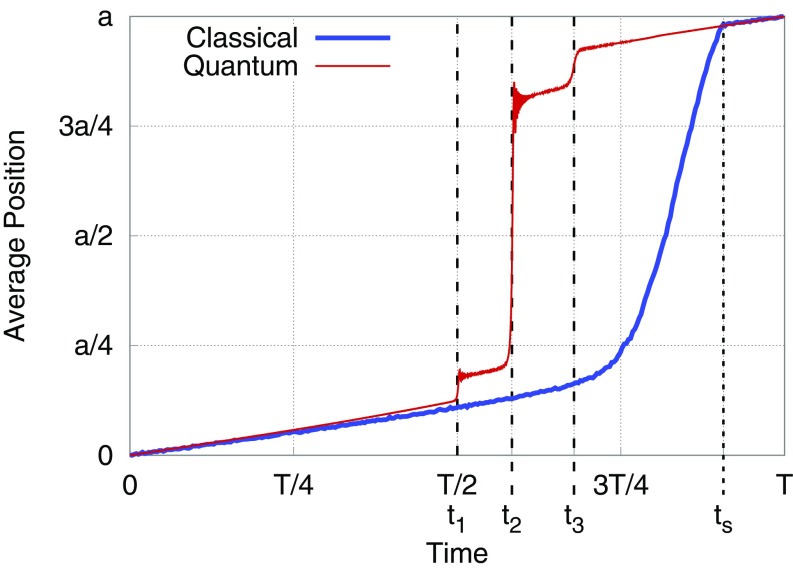
The mechanism just described predicts an advancement of the average position of the particle as well as a corresponding onset of dissipated power that are very different from those of ordinary Langevin frictional dynamics (18), which, with all parameters except $\mathrm{\hslash }$ are the same as in the quantum case, would describe the classical forced sliding of the same particle. Fig. 5 compares the average particle position versus time in the quantum and classical cases. The “quantum slips” occur rather suddenly, on an LZ tunneling time scale (22) $t_{nn\prime }^{\mathrm{tunn}}$ that we can estimate to be much smaller than the period $\mathrm{T}$—$t_{nn\prime }^{\mathrm{tunn}}/\mathrm{T}=\sqrt{4\pi \mathrm{\hslash }v/(a^2{\alpha }_{nn\prime })}\approx 6\cdot {10}^{-3}$ for the relevant $t_2$ transition of Figs. 4 and 5—reflecting the abruptness of level crossing events and connected barrier passage. In particular, the main quantum slip occurs, for the parameters used in Fig. 5, precisely when the instantaneous Wannier ground level of the left well is resonantly aligned with the first excited Wannier level in the neighboring well.

Fig. 5.

Average position of the particle vs. time, in the quantum (red) and classical (blue) cases. Parameters are identical to those of Fig. 4. Most of the “slip” of the quantum particle goes through the excited-state resonant tunneling, taking place at $t_2$ beyond the symmetric moment $t_1=\mathrm{T}/2$ between the two potential wells. The dashed line shows the position of the classical “spinodal” moment $t_s$, where the $x=0$ local potential minimum disappears and the particle is forced to slip.

Because it occurs at a lower spring loading, the resonant barrier permeation strongly reduces the overall mechanical friction work exerted by the pulling spring. Fig. 3 shows the amount of energy absorbed by the bath (friction) at the end of each period as a function of velocity. In the classical case, for time scales much shorter than the characteristic thermal hopping of the barrier, friction grows logarithmically with speed, due to thermally activated slip, as is well known for stick–slip at finite temperature (1, 23–25)

$$W_{cl}=b+c{\ln }^{2/3}\left(dv\right),$$ [6]

with constants $b=28.8E_R$, $c=8.49E_R$, and $d=6.81\cdot {\mathrm{\hspace{0.17em}10}}^4\mathrm{\hslash }/E_{R}a$ providing the best fit in our case.

The quantum dissipation rate is by comparison, within the present parameter choice, smaller by a factor $\sim 3$. It is well approximated through the LZ probabilities (Eq. 3) of transition from the $n^{\text{th}}$ to the ${(n+1)}^{\text{th}}$ eigenstate:

$$W_q(v)\approx P_{0\to 1}(v)\left[(1-P_{1\to 2}(v))\left(E_1-E_0\right)+P_{1\to 2}(v)\left(1-P_{2\to 3}(v)\right)\left(E_2-E_1\right)\right],$$ [7]

with ${\mathrm{\Delta }}_{01}=5.19\cdot {10}^{-2}{E}_R$, ${\mathrm{\Delta }}_{12}=3.03\cdot {10}^{-1}{E}_R$, ${\mathrm{\Delta }}_{23}=8.83\cdot {10}^{-1}{E}_R$, ${\alpha }_{01}=1.43\cdot {10}^2{E}_R/a$, ${\alpha }_{12}=1.38\cdot {10}^2{E}_R/a$, ${\alpha }_{23}=1.46\cdot {10}^2{E}_R/a$, $v_{0\to 1}=2.96\cdot {10}^{-5}{E}_{R}a/\mathrm{\hslash }$, $v_{1\to 2}=1.05\cdot {10}^{-3}{E}_{R}a/\mathrm{\hslash }$, and $v_{2\to 3}=8.40\cdot {10}^{-3}{E}_{R}a/\mathrm{\hslash }$. Dissipation requires in fact, to start with, that the system does not LZ tunnel, so that $P_{0\to 1}>0$. The amount of power absorbed by the bath equals the probability to populate the first and higher excited states times their energy difference with the ground state. This analytical prediction is found to match the numerical results for low velocities in Fig. 3 and can be used to show the characteristic behavior in the $v\to 0$ limit, where simulations become exceedingly expensive, as highlighted in the Inset. We should note that Eq. 7 is approximate first of all because it does not include higher excited states; moreover, it is only valid when velocity is low enough that the cooling rate ${\gamma }_c\gg {\mathrm{T}}^{-1}=v/a$, and the particle loses all its kinetic energy before encountering the subsequent slip, which is not satisfied for the larger velocities. Within this regime, however, it also shows how dissipation is not dependent on the bath coupling strength $\alpha$. Unless temperature is too high, quantum tunneling through the barrier always preempts classical negotiation of the barrier, causing friction to be necessarily smaller than classical friction. In this sense, we can speak of quantum lubricity.

This conceptually simple form of quantum lubricity might, in some variant, be within experimental reach for cold ions in optical lattices. The parameters used in our simulations assume a particle with the mass M of ¹⁷¹Yb, and a lattice spacing $a=500$ nm. The lattice potential is taken to be $U_0=38.5E_R$, in terms of the recoil energy $E_R=\pi {}^2\mathrm{\hslash }^2/(2M{a}^2)$. The corrugation parameter $\eta ={({\omega }_l/{\omega }_0)}^2$, defined (9) as the confinement ratio of the lattice intrawell vibrational frequency ${\omega }_l=2\sqrt{U_0{E}_R}/\mathrm{\hslash }$ to the harmonic trap (the pulling spring) vibrational frequency ${\omega }_0=a\sqrt{2k{E}_R}/\pi \mathrm{\hslash }$, is set equal to $\eta =4$, so that the overall potential energy has just two minima. This automatically sets the value of the spring constant at $k=190E_R/a^2$. Finally, the assumption of a weakly coupled Ohmic environment, with $\alpha =0.002$ and ${\omega }_c=12E_R/\mathrm{\hslash }$, necessary here for a consistent perturbative theory, is not mandatory, as we have seen, for an experimental realization and can anyway be realized by a judicious choice of cooling strengths. The values adopted for $\alpha$ and ${\omega }_c$ correspond to a cooling rate ${\gamma }_c\approx 0.018E_R/\mathrm{\hslash }$. To make the bath effective during the dynamics, the condition on the driving velocity $v<{\gamma }_{c}a$ must be satisfied, leading to a time scale much larger than the period of vibrations in the lattice well: $v/a\ll {\omega }_l$. It may be useful to mention here what might happen for very different coupling strengths. For excessively weak coupling, the bath would fail to absorb the work done on the particle, whose increasing energy will lead to a classical trajectory. Conversely, excessively strong coupling, not accessible by our perturbative QME scheme, would inherently perturb the coherent dynamics, eventually destroying tunneling and quantum lubricity altogether. Finally, we note that our choice of temperature $T=1E_R/k_B$ was deliberately low compared with the lowest temperatures achievable in this kind of experiment, to better emphasize the kind and nature of quantum effects. However, theoretical studies (20) suggest that LZ tunneling is very robust and transition probabilities are only slightly modified even at temperatures much higher than the minimum gap. Indeed, even in our simulations, where $k_{B}T\simeq 3{\mathrm{\Delta }}_{12}$, the transition probabilities show only small deviations from the ideal LZ formula.

Conclusions

In summary, comparison of classical stick–slip with quantum friction for a particle sliding in a periodic potential foreshadows major differences. A classical particle slides from a potential well to the next by overcoming the full potential barrier, whereas a quantum particle can permeate the barrier by LZ resonant tunneling to a discrete level in the nearby well, a process suddenly and narrowly available at a well-defined position of the harmonic trap, leading to discontinuous forward jump, as shown in Fig. 5. This quantum slip preempts the classical slip, giving rise to quantum lubricity. The potential energy accumulated by the particle during sticking, and frictionally dissipated after the quantum slip, is just the amount sufficient to reach the resonant condition with the excited state in the next well. Conversely, the classical potential energy increase necessary for classical slip is close to the top of the barrier, with a correspondingly larger amount of dissipated energy during and after the slip. In addition to this quantum lubricity effect, a regime of quantum superlubricity is in principle expected at sufficiently low temperatures, where the friction decay with velocity decreasing to zero should be nonanalytical, with all derivatives equal to zero. It will be of interest in the future to pursue these quantum novelties in more detail, as soon as experimental realizations for single and many-particle systems will emerge.