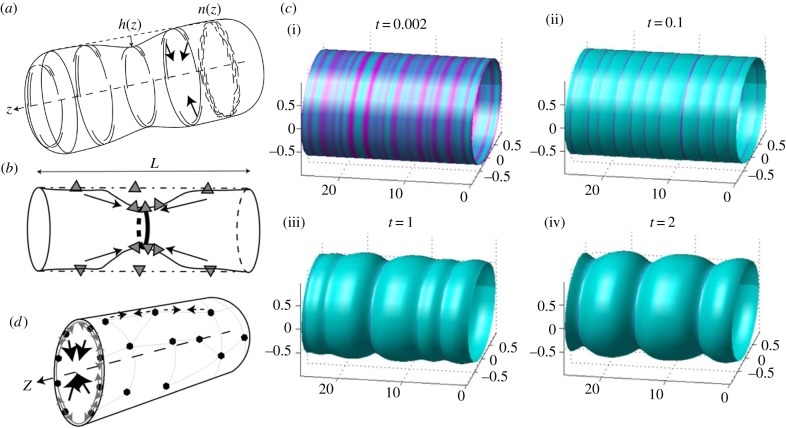
Figure 3.

(a) Positive feedback between convex (concave) CMC (short and long arcs) that adsorb to the inner (outer) side of a membrane tube and recruit forces of the cytoskeleton towards the tube axis (arrows) [34], either due to contraction or protrusive forces from the outside [87]. The rings show that the CMC are taken to be uniformly distributed around the circumference (axial symmetry). Arc-like CMC that are aligned along the circumference of the tube (as shown) sense mainly the radius of curvature of the tube. (b) Concave (convex) CMC (triangles) that adsorb on the inside (outside) of the membrane tube and are mostly aligned along the axis, and are therefore sensitive also to the curvature in the axial direction [87]. In this case, the positive feedback is due to the high curvature at the tip of the constriction, similar to the process shown in figure 2a for flat membranes. (c) Numerical simulations [88] of cylindrically symmetric distribution of convex CMC in the unstable regime, where small initial fluctuations (i) spontaneously grow to become condensed rings at the separation of the most unstable wavelength (ii). At longer times, nonlinear effects drive the coarsening of the rings into fewer and thicker rings (iii,iv). From Shlomovitz & Gov [88]. (d) A cortical actin–myosin network (thin polygons with filled circle nodes) that is adsorbed to the membrane can give rise to contractile forces (dashed lines with small arrows) that squeeze the tube towards its axis (large arrows pointing at the tube axis) [87]. (a)–(d) From Shlomovitz & Gov [87].