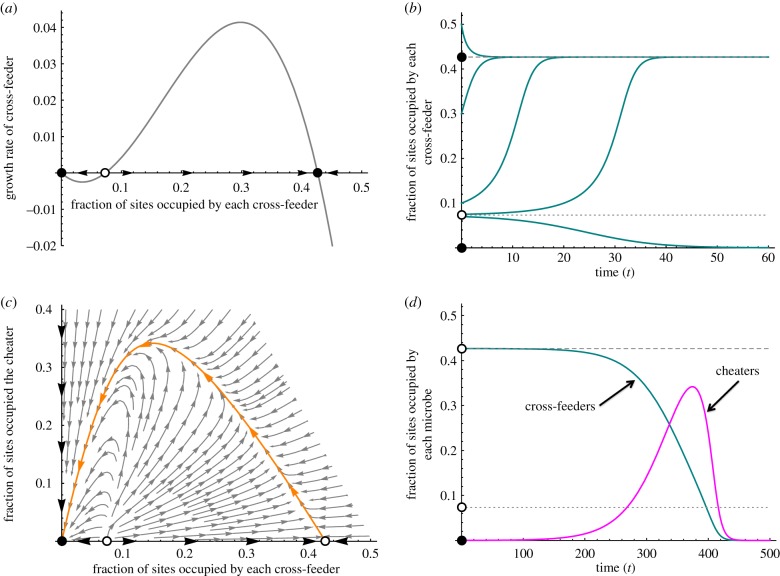
Figure 3.

Results of the mean-field model. (a) A system without cheaters will have at most three equilibria: a stable extinction equilibrium, a stable positive equilibrium and an unstable equilibrium separating them. (b) If the cross-feeders begin at a density above the unstable equilibrium, they will converge on the positive equilibrium. If they begin below the unstable equilibrium, they go extinct. (c) If a cheater is introduced, the positive equilibrium becomes unstable, and no new equilibria are created. (d) Thus, cheaters drive the cross-feeders extinct and then die off. In each figure, b₁ = b₂ = 0.6, b₀ = 0.7, Q = 4 and δ = 0.15. (Online version in colour.)