Does the handicap principle explain the evolution of dimorphic ornaments?

Highlights

• •We reinvestigate a new model based on the handicap hypothesis.
• •We show the handicap hypothesis does not explain male dimorphisms.
• •The results are due to the ‘playing-the-field’ assumption of the model.
• •The generality of the ‘playing-the-field’ assumption is suspect.
• •The evolutionary stability of the proposed new equilibrium is questionable.

Many species are sexually dimorphic and, interestingly, males in some species are dimorphic themselves: some males develop weapons and ornaments, whereas others express rudimentary ornaments or none at all (horned beetles, Onthophagus taurus: Emlen et al., 2007, Moczek and Emlen, 2000; bluegill sunfish, Lepomis macrochirus: Dominey, 1980, Gross and Charnov, 1980; ruffs, Philomachus pugnax: Lank, Smith, Hanotte, Burke, & Cooke, 1995; for a review see Simpson, Sword, & Lo, 2011). Males can be so extremely dimorphic that the morphs have been misclassified as different species. The selective maintenance of such male dimorphisms has been difficult to understand (Simpson et al., 2011). Yet, a recent paper by Clifton et al. (2016) concluded the evolution of male dimorphisms can be explained solely by the handicap principle (Zahavi, 1975). It is not intuitively obvious how the handicap principle can selectively maintain male dimorphisms, and no verbal explanations were provided. Here, we raise several caveats about this recent study and, in particular, we show that the findings are not generated by the handicap principle, but by an unrelated assumption of the model. This assumption is not unreasonable, but its stability needs to be examined before concluding that it provides an explanation for the evolution of male dimorphisms.

There are many versions and interpretations of the handicap hypothesis, but it is unclear which version was implemented for the authors' new model. This omission makes it impossible to understand the novelty of the model and how it succeeds in explaining male dimorphisms or why others failed. The authors cite the original handicap hypothesis (Zahavi, 1975), and yet this version does not work (reviewed in Kirkpatrick 1986). They also cite evidence consistent with subsequent versions of the handicap hypothesis, but do not acknowledge that there are many models (Hurd, 1995, Lachmann et al., 2001, Számadó, 1999, Számadó, 2011) and empirical studies (Kotiaho, 2001, Moreno-Rueda, 2007) that do not provide support (Számadó & Penn, 2015). The version of the handicap hypothesis that received theoretical support is the‘strategic handicap’ model (Zahavi, 1975, Grafen, 1990). Grafen (1990) concluded that costly ornaments provide honest indicators of male quality when the fitness costs of signalling are greater for low- than high-quality individuals. The three main conditions in Grafen's model correspond to the main assumptions of the authors' model: (1) ornament size is an honest signal of health, as it is assumed that optimal ornament size is an increasing function of health; (2) increasing ornament size is costly; and (3) healthier individuals can better afford the costs of producing larger ornaments (i.e. differential cost assumption). The authors did not claim to base their model on Grafen's version, and instead used their own interpretation of Zahavi’s (1975) handicap principle (S. Clifton, personal communication). This is understandable given the limitations of Grafen's model (Getty, 1998, Getty, 2006, Hurd, 1995, Lachmann et al., 2001, Számadó, 1999, Számadó, 2011; see Számadó & Penn, 2015 for a recent overview and discussion). However, there is a crucial and unstated difference between these models, and particularly the shape of the benefit function used in Grafen's (1990) versus the authors' model. Here we show that the results of the authors' model are due to the shape of the benefit function, which, to our knowledge, is not part of any versions of the handicap hypothesis. This means that either the results of the authors' new model are not driven by the handicap hypothesis or the authors are proposing a novel version of the handicap hypothesis.

The critical assumption that drives the results of the authors' model is the shape of the benefits function and, therefore, we examined this assumption (see Appendix for a description of the main details of the authors' model). For simplicity, we consider the difference between the fitness at the optimal ornament size, given by the ‘individual reproductive potential’ (φ^(ind)) function, and the fitness at the actual ornament size to be the cost function (c) of signalling, since it provides the cost of deviating from the individual optimum. The study also applies Grafen's condition to this function (i.e. cost and differential cost). We consider the ‘the social reproductive potential’ (φ^(soc)) in the model to be the benefit function (b), since this function provides the benefit (reproductive success) of the enlarged ornament. The study sets up two conditions (see below) for the emergence of two or more morphs: the first condition specifies that ‘Individual effects dominate reproductive potential for large ornament sizes’ (‘condition (i)’, page 5), and the second specifies that ‘Social effects dominate reproductive potential for at least some range of ornament sizes greater than the population mean’ (‘condition (ii)’, page 5). Together, these conditions imply that there must be an inflection point, where the function switches from convex to concave, or vice versa, in either the cost or the benefit function. Without an inflection point, either the first or second condition is satisfied but not both. Yet, neither Grafen's (1990) model, nor any other versions of the handicap hypothesis, include any such inflection point, and therefore cannot explain the results.

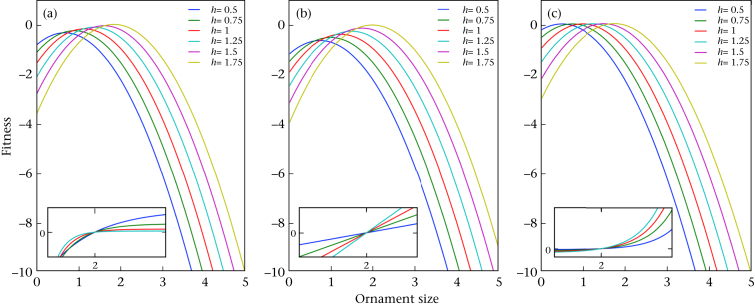
The inflection point is introduced in the benefit function of the authors' model, and the numerical example presented in the paper clearly shows that the handicap hypothesis does not explain the results (see Fig. 1a). This inflection point in the benefit function arises entirely from the assumption in the model that the fitness of an individual depends on the population average (‘playing-the-field’ model, Maynard Smith, 1982; p. 23), rather than one or a series of individual opponents, as with other evolutionarily stable strategy models. The bimodal fitness curves, and hence the bimodal distribution of ornament size, are the result of this inflection point. If the benefit function has no inflection point and the cost function, which follows the assumptions of the Zahavi/Grafen handicap hypothesis, is not changed, then there is no such effect. These arguments can be illustrated by numerical examples (see Fig. 1). We used the same cost function from the authors' study, but then also introduced a benefit function that lacks an inflection point, although otherwise behaves exactly as the benefit function in the authors' study (i.e. monotonically increasing with ornament size and a zero value at the population average). We investigate three different general types: a convex, a linear and a concave function. Fig. 1 shows the results for different gammas (γ), which describe the ‘social sensitivity’ or the strength of sexual selection. It is clear that the new fitness functions have only one optimum, even though the cost function remains unchanged and Grafen's (1990) second and third conditions (cost and differential cost) still hold. We do not assume that the benefit functions used in these three examples are realistic, but they show that Grafen's handicap conditions are not sufficient to explain the observed bimodal fitness curves in this new model. All in all, the playing-the-field assumption in the authors' model is reasonable, but, to our knowledge, it is not part of any version of the handicap hypothesis.

Figure 1.

Fitness curves with three different benefit functions (concave, linear and convex respectively). The cost function is the same as that in Clifton et al. (2016) with Grafen's handicap conditions. Insets show the benefit functions (the social reproductive potential, φ^(soc)), where: (a) φ^(soc) = 1−e^(−aγ)−(1−e^(−āγ)), ā = 2; (b) φ^(soc) = aγ−āγ, ā = 2; (c) φ^(soc) = e^(a−ω)γ−e^(ā−ω)γ, ω = 5, ā = 2.

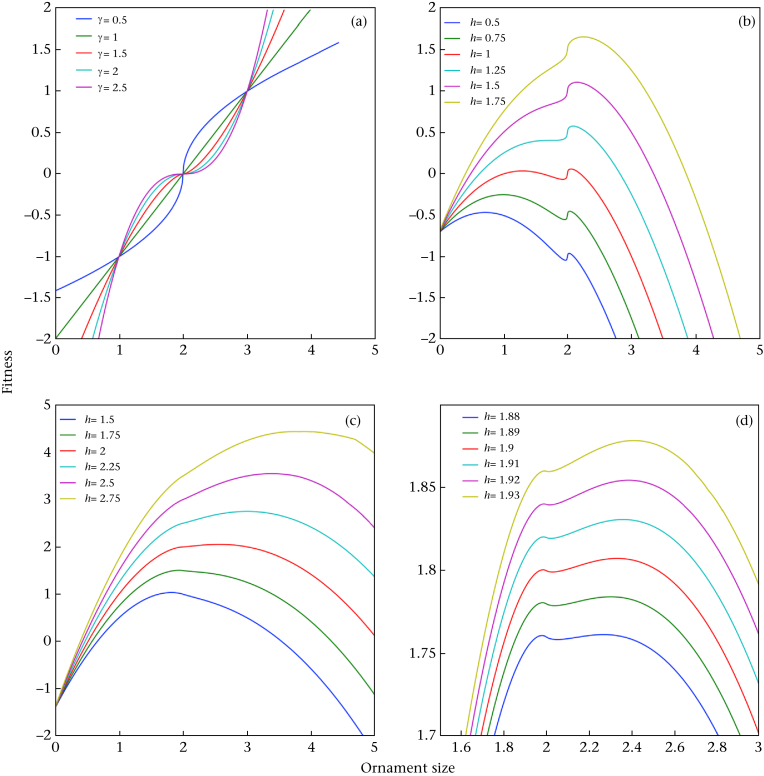
Finally, regardless of the relevance of the handicap hypothesis, it is unclear that the authors' model provides a general explanation for the evolution of dimorphic male ornaments. First, closer examination indicates that the bimodal fitness function is typical only in a narrow range of conditions (what the authors refer to as health, h). Fig. 2 shows the fitness as a function of ornament size for various health values. It is clear from this figure that bimodality is observed in only a few cases. The effect is more pronounced for γ values <1 (see Fig. 2b γ = 0.5), and the effect is almost negligible for γ values larger than 1 (see Fig. 2c). Fig. 2d is an enlarged section from Fig. 2c, illustrating the effect more clearly, and shows that the result holds for only a narrow range of health values (ca. 1.9). Note that the scale on the x-axis is not indicated on Fig. 2c or 2d in the original study (page 2).

Figure 2.

(a) The original benefit function (the social reproductive potential, φ^(soc)), and the fitness curves for different values of γ, as a function of ornament size (a), assuming an average ornament size ā = 2. (b) γ = 0.5, (c) γ = 1.5 and (d) γ = 1.5, enlarged section of (b).

Second, the evolutionary stability of the signalling equilibrium proposed in this new model was not investigated, but seems doubtful. The paper proposes a novel type of signalling equilibrium, in which signallers of the same type can send more than one signal, and yet the receiver response to this signalling strategy was not investigated. It is simply assumed to be evolutionarily stable. However, at any stable evolutionarily equilibrium, the signaller's strategy must be the best response to the receiver's strategy, and vice versa (Bergstrom, Szamado, & Lachmann, 2002). Without this crucial step, signalling models are incomplete at best and potentially misleading. The approach used in constructing this new model appears to be based on calculating a ‘signalling equilibrium’ by searching only for the optimal signal intensity for signallers and keeping the receivers' evolutionary response fixed. Here we explore why the current shape of the receiver's response may not be the best response to the signaller's strategy described in the Clifton, Braun, and Abrams (2016) model. The authors argue that communication is ‘mostly honest, at least for large enough variance in health.’ This conclusion might apply to certain scenarios. (1) The receiver can discriminate all signals, and thus it can effectively assess the quality of the signaller. If so, it should give the same response, as dictated by the receiver's optimum allocation, to the two morphs that have to the same health. In turn, this implies that one of these signals is redundant (the costlier one), and thus it will be selected against; hence the scenario is not evolutionarily stable. (2) The other scenario is that some of the signals cannot be differentiated from signals used by other types. Receivers in such situations are expected to react to the average type expected (Bergstrom & Lachmann, 1998), and thus they will allocate resources accordingly. If so, the morph with the lower signal cost will have higher fitness and the other signal will be selected against; this scenario is not expected to be evolutionarily stable. Thus, it is unclear that the receiver's strategy assumed by the authors is the best response to the signaller's strategy obtained in the authors' model, and making conclusions about the evolutionary stability of this model crucially require investigating the coevolutionary response of receivers.

In summary, the model proposed by Clifton et al. (2016) to explain male dimorphisms is interesting, but several caveats should be considered. First, there are many versions of the handicap hypothesis, but the authors did not clarify which was the basis of their model; nor did they acknowledge the limitations of the relevant version that has theoretical support (i.e. the Zahavi–Grafen version). Second, the results of the authors' model do not arise from the handicap hypothesis per se, but from an inflection in the benefit function that emerges from the ‘playing-the-field’ assumption. The conclusion of the paper (‘Handicap principle implies emergence of dimorphic ornaments’) is therefore misleading, or at least it requires a new version or reinterpretation of the handicap hypothesis. Third, the ‘playing-the-field’ assumption is reasonable, but the generality of the results appear rather limited (since bimodality is generated only in a narrow range of parameters for gamma values >1). Such limitations could be useful if they provided predictions for the conditions in which male dimorphisms are expected to evolve (e.g. see Emlen et al., 2005, Tomkins and Brown, 2004), but we could not detect any such predictions. Also, the conclusions about evolutionary stability of this model are premature until the coevolution of the receivers' responses are investigated, and the evolutionary stability of the receiver's strategy in this model is doubtful. We applaud the authors for the novelty of their approach to address this difficult problem, but this new model is unlikely to provide a general explanation for male dimorphism, at least in its current form. There are other viable hypotheses to explain dimorphic male phenotypes, including ‘mimicry, sneaking and fighting,’ as the authors acknowledged, and these deserve more attention.

MS. number: 17-00560

Appendix.

Clifton et al. (2016) model the change in the distribution of male ornament size due to selection on the differential fitness effect of ornaments with different sizes. The fitness of individuals is influenced by the cost of the ornaments (called ‘individual reproductive potential’, φ^(ind)) and by the reproductive benefits of the ornament (called ‘social reproductive potential’, φ^(soc)). The overall fitness is a weighted sum of these two factors:

$$\mathrm{\phi }=s{\mathrm{\phi }}^{\left(\text{soc}\right)}+\left(1-s\right){\mathrm{\phi }}^{\left(\text{ind}\right)}=sa\left(2a_{\text{opt}}-a\right)+\left(1-s\right)\mathrm{sgn}\left(a-\overline{a}\right){\left|a-\overline{a}\right|}^{\gamma }$$ (1)

where a denotes ornament size, s is the relative importance of ‘social effects’ versus ‘individual effects’ and γ describes the sensitivity of the ‘social reproductive potential’ to deviations from the population mean. Accordingly, the first part of equation (1) gives the value of ‘social reproductive potential’ and the second part is the ‘individual reproductive potential’.