Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Aug 1.
Published in final edited form as: Magn Reson Med. 2017 Dec 19;80(2):641–647. doi: 10.1002/mrm.27047

Quadrupolar Jump-and-Return Pulse Sequence for Fluid-Suppressed Sodium MRI of the Knee Joint at 7 T

Ding Xia 1, Jae-Seung Lee 1, Ravinder R Regatte 1
PMCID: PMC5910252  NIHMSID: NIHMS923445  PMID: 29266468

Abstract

Purpose

To demonstrate the feasibility of the so-called quadrupolar jump-and-return (QJR) pulse sequence by assessing its performance on the contrast modification to knee cartilage and quality of fluid suppression in the knee joint in vivo at 7 T.

Methods

The right knee joints of five healthy volunteers [3 males (mean age = 32.4 ± 1.3 years) and 2 females (mean age = 27.9 ± 1.0 years); mean age = 30.6 ± 2.7 years] were scanned on a 7 T scanner with varying the delay in the QJR sequence from 1 ms to 5 ms. For one healthy volunteer, the QJR scan with the delay of 3 ms and the inversion-recovery (IR) scan were performed. Numerical simulations were conducted to evaluate the effects of B0- and B1-field inhomogeneities and residual quadrupolar couplings on fluid suppression and tissue contrast, respectively.

Results

The QJR sequence suppressed the fluid signal from the artery and produced the contrast of knee cartilage in vivo. Its performance was comparable to that of the conventional IR sequence. Numerical simulations suggested that the fluid suppression may not be affected much by field inhomogeneities, but that a distribution of residual quadrupolar couplings and weak RF pulses may interfere with the clear interpretation of cartilage contrast.

Conclusion

This preliminary work demonstrated that the QJR pulse sequence produces contrast for knee cartilage while suppressing the fluid signal from the artery. The knee cartilage contrast and quality of fluid suppression obtained from the QJR sequence were comparable to those of the IR sequence.

Keywords: Quadrupolar, Jump-and-Return, Sodium, Knee

INTRODUCTION

The extracellular matrix of articular cartilage is mainly composed of water, collagen, and proteoglycans (PGs) [1–4]. Collagen and PGs provide the extracellular matrix with its ultrastructure and osmotic pressure, respectively, which together characterize the mechanical properties of articular cartilage. In PGs, a protein core may have many glycosaminoglycan (GAG) chains attached to it. The GAG chains are negatively charged, so a negative fixed charge density (FCD) is established in cartilage. Therefore, cations like Na+ may be attracted to the tissue, which in turn creates osmotic pressure and introduces water molecules [11]. It has been demonstrated that the loss of PGs is related to the degradation of cartilage tissues in diseases like osteoarthritis (OA) and degenerative disc diseases [5–8].

The negative FCD in cartilage makes 23Na MRI useful for evaluating the contents of GAGs or PGs [9,10]. In the knee joint, sodium ions may exist in the cartilage tissues as well as in the synovial fluids, and a contrast between the cartilage tissues and fluids would improve the sensitivity of the sodium MRI to the loss of PG in patients with OA [12]. One prevailing sequence for generating the cartilage tissue contrast have been inversion recovery (IR) [13,14], which exploits the fact that the spin-lattice relaxation time of sodium is longer in the fluid compartments than in the cartilage tissue compartments [15].

In addition to the shorter spin-lattice relaxation time, sodium ions in cartilage may be subject to residual quadrupolar couplings due to the anisotropic surroundings provided by the ultrastructure of the extracellular matrix [16]. Ex vivo cartilage studies have shown that residual quadrupolar couplings may increase with tissue degradation [17–19]. One simple method for generating a contrast between the environments with and without residual quadrupolar couplings would be the so-called quadrupolar jump-and-return (QJR) sequence [20]. While the conventional jump-and-return sequence separates signals based on the chemical shift difference between two spin species [21,22], the QJR sequence works particularly on a spin-3/2 system and excites signals based on residual quadrupolar couplings.

In this work, we implemented the QJR pulse sequence for 23Na MRI of the knee joints in vivo. Its performance was assessed in terms of cartilage tissue contrast and quality of fluid suppression while varying its delay. Then, the cartilage tissue contrast and fluid suppression at a chosen delay were compared to those produced by the IR sequence. Finally, the effects of B0- and B1-field inhomogeneities and a distribution of residual quadrupolar couplings were briefly addressed through numerical simulations.

METHODS

Quadrupolar Jump-And-Return Pulse Sequence

A jump-and-return or 1—1 binomial sequence consists of two pulses with the same flip angle and a delay inserted between them. It is usually used for solvent suppression in nuclear magnetic resonance (NMR) spectroscopy and fat suppression in imaging [21–25]. Depending on the relative phases of the two pulses, one may excite or suppress signals selectively at the frequency offsets determined by a given delay. The signal intensity excited by this sequence will reach the maximum when the flip angle of the pulses is 45°.

In contrast to the conventional jump-and-return sequence, the QJR sequence works for a spin 3/2, such as 7Li and 23Na. It selectively suppresses a spin species if its residual quadrupolar coupling satisfies the condition 2πfQτ = n, where fQ is the quadrupolar splitting in Hz, τ is the delay, and n = 0, 1, 2, …. The quadrupolar splitting fQ is the frequency difference between the central and satellite peaks, which is proportional to the residual quadrupolar coupling [26]. The QJR sequence maximizes the signal intensity of the selected spin species when fQτ = (2n − 1)/2 with n = 1, 2, 3, … [20]. While the total signal intensity does not increase, the QJR sequence focuses it onto the central peak, which is beneficial to MRI applications. When the flip angle of the pulse is the magic angle, the satellite peaks are suppressed and the central peak is enhanced by a factor of 2 compared to that excited by a 90° pulse from the thermal equilibrium state, which is about 94% of the theoretical maximum. In this work, the QJR sequence is referred to one with the flip angle of the pulses being the magic angle.

In Vivo 23Na Knee 3D MRI

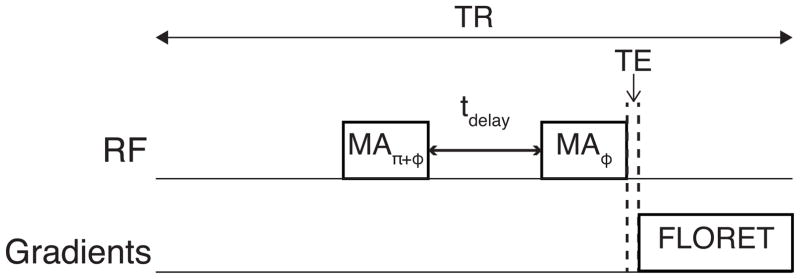
After approval from the institutional review board of the New York University Langone Medical Center and signed informed consent, the right knee joints of five healthy volunteers (3 males [mean age = 32.4 ± 1.3 years] and 2 females [mean age = 27.9 ± 1.0 years]; mean age = 30.6 ± 2.7 years) were scanned on a 7 T Siemens scanner with an in-house built double-tuned knee coil with eight 23Na channels and four 1H channels [27]. The knee images were acquired with Fermat looped, orthogonally encoded trajectories (FLORET [28]) consisting of 3 hubs at 45°, each of which comprises 332 interleaves. The common parameters for the image acquisition were as follows: field of view (FOV) = (220 mm)3, echo time (TE) = 0.2 ms, Nyquist resolution = 3.4 mm, the acquisition time = 6.6 ms, and the number of averages = 6. The durations of RF pulses were 0.4 ms and 0.6 ms for the magic-angle and 90° pulses, respectively. The schematic of the pulse sequence for QJR 23Na MRI is presented in Fig. 1. Note that the delay tdelay between two magic-angle pulses is defined from the end of the first pulse to the beginning of the second pulse.

Figure 1.

Figure 1

Open in a new tab

Schematic of the pulse sequence for QJR 23Na MRI. The flip angle of two RF pulses is the so-called magic angle (MA), and their phases are separated by π. ‘FLORET’ indicates Fermat looped, orthogonally encoded trajectories [28].

First, one reference and five QJR 23Na knee 3D MRI data sets were obtained for each volunteer with tdelay varied from 1 ms to 5 ms. With the repetition time (TR) set to be 100 ms, the scan time per each 23Na knee 3D MRI dataset was about 10 min. Taking into account this rather short TR, the reference images were acquired with the magic-angle pulse, instead of a 90° pulse.

Second, 23Na knee 3D images were acquired with the QJR and IR sequences for one volunteer. To allow the recovery of the suppressed fluid signal during the IR scan, TR was set to be 140 ms, so the scan time per image was about 14 min. For the IR scan, the durations for the 180° inversion and 90° excitation pulses were 1.2 ms and 0.6 ms, respectively. The recovery delay (TI) was 24 ms, which was defined as the time interval from the end of the 180° pulse to the beginning of the 90° pulse. For the reference scan, the same 90° excitation pulse was used. For the QJR scan, the duration of the magic-angle pulses was 0.4 ms, and tdelay was 3 ms.

23Na Image Data Processing

The 23Na images were reconstructed by using standard 3D regridding [29]. The matrix size was 128×128×128 with the nominal resolution of 2 mm. The signal intensities measured with the QJR and IR sequences were normalized voxel-by-voxel to the signal intensities of the reference scan. For individual volunteers, six regions of interest (ROIs) were defined on the artery, patella cartilage, lateral and medial femorotibial cartilage, and lateral and medial femoral condyle cartilage. The distributions of the normalized signal intensities were compared among the QJR images with different tdelay values and between the QJR and IR images.

Numerical Simulations

First, the performance of the fluid suppression for the spin species with fQ = 0 was evaluated by numerically solving the Bloch equations. The components of the magnetization vector at the end of the jump-and-return sequence were obtained at the frequency offsets from -160 Hz to +160 Hz, every 10 Hz. The flip angle of the pulses was changed from 0° to 100.8° with the step size of 1.44°, and tdelay was set to be 3 ms.

Second, the signal intensities from quadrupolar-coupled spin-3/2 species were calculated by numerically solving the quantum master equation [30]. For the central and satellite transitions, tr{I-ϱ}/tr{Iz2} was evaluated at the end of the QJR sequence, where tr{O} indicates the trace of an operator O, ϱ is the density operator at the end of the QJR sequence, I− = Ix − iIy, and Ix, Iy, and Iz are the x, y, and z components of the spin angular momentum. The quadrupolar splitting fQ was varied from 0 kHz to 2 kHz with the step size of 0.01 kHz. The frequency offset and flip angle of the pulses were set to be zero and the magic angle, respectively.

For both the simulations, the duration of the pulses was 0.4 ms, and no relaxations were assumed.

RESULTS

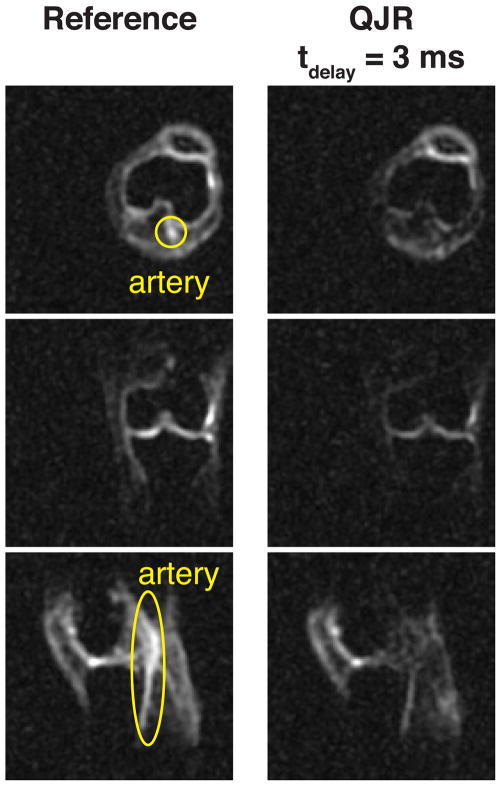
The representative slices from the reference and QJR 23Na knee 3D MRI datasets are presented in Fig. 2 and Supporting Figure S1. The artery is clearly observable on the axial and sagittal knee slices from the reference scan but barely visible on the corresponding slices from the QJR scans. The contrast for cartilage tissues seem to be well retained in the QJR scans and may vary with tdelay.

Figure 2.

Figure 2

Open in a new tab

Slices from 23Na images of the right knee of a healthy volunteer. The slices in the leftmost column are from the reference scan, performed without the first pulse of the QJR sequence shown in Figure 1. The artery is indicated by yellow ovals.

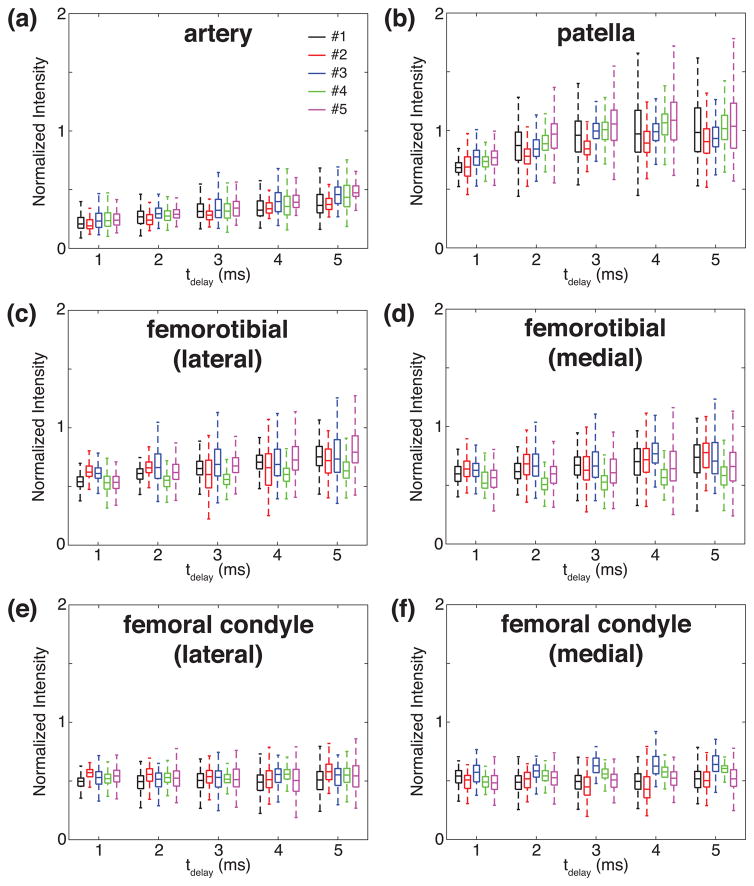
The box plots of the normalized signal intensities against tdelay are presented in Fig. 3, for individual ROIs and volunteers. In those artery ROIs, the normalized signal intensities grow along with tdelay, as seen in Fig. 3(a). In the patella ROIs, they increase until tdelay reaches 3 ms and stay at the similar level for the longer tdelay, as seen in Fig. 3(b). In the femorotibial regions, the medians of the normalized signal intensities fluctuate with tdelay while the variances increase, as seen in Figs. 3(c) and 3(d). In the femoral condyle regions, the medians and variances of the normalized signal intensities seem unchanging as tdelay varies, as shown in Figs. 3(e) and 3(f).

Figure 3.

Figure 3

Open in a new tab

Box plots of the normalized signal intensities in the selected ROIs as a function of tdelay. (a) The artery, (b) patella cartilage, (c) lateral femorotibial cartilage, (d) medial femorotibial cartilage, (e) lateral femoral condyle cartilage, and (f) medial femoral condyle cartilage.

The representative slices from the reference, QJR, and IR knee scans are presented in Fig. 4. Both the QJR and IR sequences well suppress the fluid signal from the artery, which is visible in the axial and sagittal slices from the reference scan. In Supporting Figure S2, the normalized signal intensities are compared between the QJR and IR sequences for the selected ROIs. As for the suppression of the fluid signal from the artery, the IR scan shows a better performance (p = 6.0 × 10−81). Regarding the tissue contrast, both the QJR and IR scans work in a similar way except for the patella region, wherein the signal intensities were higher with the QJR sequence.

Figure 4.

Figure 4

Open in a new tab

Comparison of contrast between QJR and IR sequences. Slices from 23Na images of the right knee of a healthy volunteer are shown. ‘Reference’, ‘QJR’, and ‘IR’ stand for the reference scan, QJR scan with tdelay equal to 3 ms, IR scan with TI equal to 24 ms, respectively. The artery is indicated by yellow ovals.

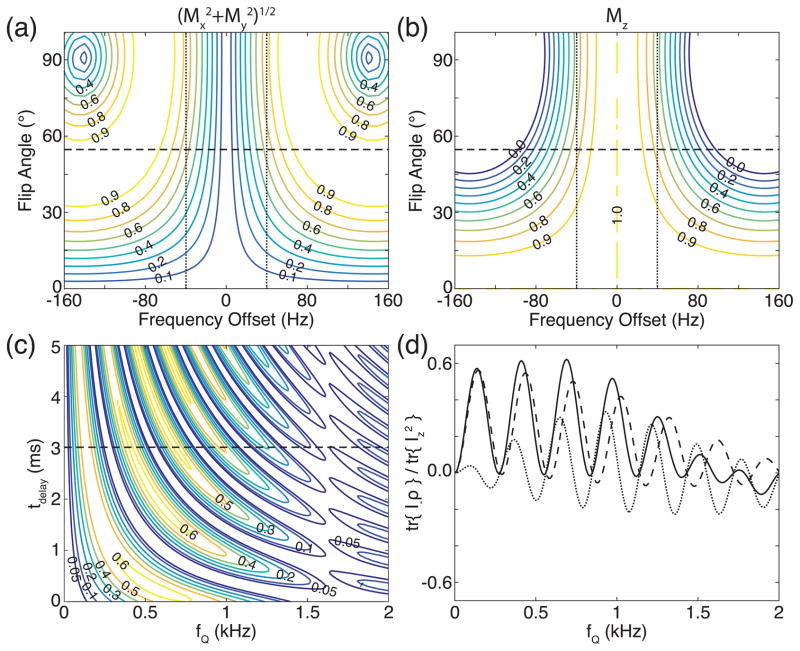
The numerically simulated transverse ( Mx2+My2) and longitudinal (Mz) components of the magnetization vector, which were evaluated at the end of the jump-and-return sequence with tdelay equal to 3 ms, are plotted in Figs. 5(a) and 5(b), respectively, against the frequency offset of the magnetization vector and the flip angle of the pulses in the sequence. Note that Mx, My, and Mz are the x, y, and z components of the magnetization vector, respectively. The performance of the QJR sequence, in which the flip angle of the pulse is the magic angle, may be followed along the horizontal dashed lines in Figs. 5(a) and 5(b). In addition, vertical dotted lines indicate the frequency offset of ±40 Hz, which correspond to ±0.507 ppm of the resonance frequency of 23Na at 7 T. Between the vertical dotted lines, the magnitude of the transverse components could be 60% along the horizontal dashed lines, although 80% of the longitudinal component is returned back.

Figure 5.

Figure 5

Open in a new tab

Numerically simulated performance of the QJR sequence. (a, b) The normalized magnitude of the (a) transverse and (b) longitudinal components of the magnetization vector at the end of the jump-and-return sequence with tdelay equal to 3 ms is plotted as a contour map against the flip angle of the pulses and the frequency offset. No residual quadrupolar couplings are assumed. The horizontal dashed line indicates when the flip angle of the pulses is the magic angle, and the vertical dotted line the frequency offset of ±40 Hz. (c) The absolute value of the normalized signal intensity is plotted against fQ and tdelay. The horizontal dashed line indicates when tdelay is 3 ms. (d) The real parts of the signal intensities are plotted against fQ. The contributions of the central and satellite peaks are represented by dashed and dotted lines, respectively.

The absolute value of the normalized signal intensities from QJR sequence is shown in Fig. 5(c), against the quadrupolar splitting fQ and tdelay. When tdelay is 3 ms, which is indicated by a horizontal dashed line in Fig. 5(c), the real parts of the signal intensities are presented in Fig. 5(d). The dashed and dotted lines are the real parts of the signal intensities of the central and satellite peaks, respectively. These plots show that the QJR sequence selects certain ranges of the residual quadrupolar couplings and that its performance gets worse as fQ increases.

DISCUSSION

Any B0-field inhomogeneities would degrade the performance of the QJR sequence implemented in this study since they cause mismatches between the phases of the transverse magnetization at the end of tdelay and the second pulse. For example, the suppressions of the signal intensities in the artery ROIs get worse as tdelay increases, as seen in Fig. 3(a). The numerical study suggests that the suppression of sodium without residual quadrupolar couplings may not be affected too seriously by B0-field inhomogeneities when tdelay is 3 ms, as shown in Figs. 5(a) and 5(b).

It is well known that the arrangement and orientation of type II collagen fibers in articular cartilage depends on the depth from the articular surface [1–4], which is one factor determining the residual quadrupolar couplings inside cartilage. With a rather crude nominal resolution of 2 mm, the signal intensity from each voxel would be the result of an average over the distribution of the residual quadrupolar couplings. Another factor governing the residual quadrupolar couplings is the direction of the B0 field with respect to the orientation of collagen [14,15,17]. The distribution of residual quadrupolar couplings may affect how the normalized signal intensity and its variance depend on tdelay.

Due to the long pulse duration, the ideal condition for the maximum signal intensity, fQτ = (2n − 1)/2 with n = 1, 2, 3, …, may not be exactly followed. From the numerical data shown in Fig. 5(d), the effective delay is estimated to be 3.4 ms by considering fQ’s at the maxima of the dashed line, which is the signal intensity due to the real part of the central transition. However, the finite pulse duration does not simply add some additional delay time to tdelay. Note that the maxima of the dashed line in Fig. 5(d) do not match the zeros of the dotted line, i.e., when the real parts of the satellite transitions are suppressed.

As seen in Fig. 5(c) and 5(d), the signal intensity decreases as fQ increases. When the quadrupolar splitting fQ is larger than the excitation range of a 400 μs-long magic-angle pulse, it selectively excites one of the three transitions, and then the QJR sequence would not work as intended. This might be one of the reasons why the signal enhancement was not observed in this study, as seen in Figs. 3 and 4. In Figs. 5(c) and 5(d), the signal intensity of the central peak is 0.4 when a 90° pulse is applied to excite the signal from the thermal equilibrium state. When Figs. 5(c) and 5(d) are compared with Figs. 3(b–f), the higher signal intensities in patella ROIs might correspond to the smaller fQ. However, a single value of fQ was assumed in the numerical simulations while a distribution of fQ’s is expected in vivo, which is not known currently. Studies with the different strengths of the B1 field may reveal more information on the distribution of fQ’s.

The QJR sequence may have advantages over the IR sequence regarding the scan time and lower specific absorption rate (SAR). The delay used in the QJR sequence is an order of magnitude shorter than the recovery delay used in the IR sequence. After the second pulse of the QJR sequence, the magnetization vector of the suppressed compartment ends up being close to the original z magnetization. Therefore, the QJR sequence may be more resilient to shorter TR. The RF power delivered by the QJR sequence would be about 40% of that by the IR sequence when the RF amplitudes of the pulses are the same. In our experiments with TR = 140 ms, the SAR values displayed on the MRI scanner were 16%, 17%, and 47% for the reference, QJR, and IR sequences, respectively. Note that the RF amplitude of the magic-angle pulses, which were 0.4 ms long, was a bit lower than that of the 90° and 180° pulses, which were 0.6 ms and 1.2 ms long, respectively.

The QJR and IR sequences may improve tissue contrast by filtering out the signals from free fluid compartments. However, 23Na MRI still suffers from its low signal-to-noise ratio and crude spatial resolution. Resolution enhancement techniques like the image registration with 1H MRI [31,32] can further improve the performance of these contrast schemes.

CONCLUSIONS

We implemented the QJR pulse sequence for fluid-suppressed 23Na MRI of knee joints in vivo. This preliminary work demonstrated that the QJR sequence produces contrast for knee cartilage while suppressing the fluid signal from the artery. The cartilage contrast and quality of fluid suppression obtained from the QJR sequence were comparable to those from the IR sequence. While the QJR sequence may have the benefits of reduced SAR and shorter scan time, the interpretation of its tissue contrast requires more information about the distribution of residual quadrupolar couplings in vivo and a better understanding of how imperfect experimental conditions, such as field inhomogeneities and weak RF power, affect the contrast.

Supplementary Material

Supp figures

Supporting Figure S1. Slices from 23Na images of the right knee of a healthy volunteer. The slices in the leftmost column are from the reference scan, performed without the first pulse of the QJR sequence shown in Figure 1. The artery is indicated by yellow ovals. The other five columns present slices from the QJR scans with varying the delay tdelay, which is displayed at the top of each column.

Supporting Figure S2. Comparison of the normalized signal intensities between the QJR and IR scans for the six selected ROIs. In each scatter plot, a dotted line is drawn to show where the signal intensities between the QJR and IR scans are equal.

Acknowledgments

Research reported in this publication was supported in part by the National Institutes of Health (grants K25AR060269, R01AR060238, R01AR067156, R01AR068966) and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (NIH P41EB017183).

References

  • 1.Meyer U, Wiesmann HP. Bone and Cartilage Engineering. Berlin: Springer; 2006. [DOI] [Google Scholar]
  • 2.Athanasiou KA, Darling EM, Hu JC. Articular Cartilage Tissue Engineering. Synth Lect Tissue Eng. 2009;1:1–182. doi: 10.2200/S00212ED1V01Y200910TIS003. [DOI] [Google Scholar]
  • 3.Buckwalter J, Mow V, Ratcliffe A. Restoration of Injured or Degenerated Articular Cartilage. J Am Acad Orthop Surg. 1994;2:192–201. doi: 10.5435/00124635-199407000-00002. [DOI] [PubMed] [Google Scholar]
  • 4.Fox AJS, Bedi A, Rodeo SA. The basic science of articular cartilage: structure, composition, and function. Sports Health. 2009;1:461–8. doi: 10.1177/1941738109350438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Hollander AP, Pidoux I, Reiner A, Rorabeck C, Bourne R, Poole AR. Damage to type II collagen in aging and osteoarthritis starts at the articular surface, originates around chondrocytes, and extends into the cartilage with progressive degeneration. J Clin Invest. 1995;96:2859–69. doi: 10.1172/JCI118357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Poole AR, Kobayashi M, Yasuda T, Laverty S, Mwale F, Kojima T, Sakai T, Wahl C, El-Maadawy S, Webb G, Tchetina E, Wu W. Type II collagen degradation and its regulation in articular cartilage in osteoarthritis. Annals of the Rheumatic Diseases. 2002;61:ii78–ii81. doi: 10.1136/ard.61.suppl_2.ii78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Lyons G, Eisenstein SM, Sweet MB. Biochemical changes in intervertebral disc degeneration. Biochim Biophys Acta. 1981;673:443–53. doi: 10.1016/0304-4165(81)90476-1. [DOI] [PubMed] [Google Scholar]
  • 8.Urban JPG, Roberts S. Degeneration of the intervertebral disc. Arthritis Res Ther. 2003;5:120–30. doi: 10.1186/ar629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Gold GE, Burstein D, Dardzinski B, Lang P, Boada F, Mosher T. MRI of articular cartilage in OA: novel pulse sequences and compositional/functional markers. Osteoarthritis and Cartilage. 2006;14:A76–86. doi: 10.1016/j.joca.2006.03.010. [DOI] [PubMed] [Google Scholar]
  • 10.Insko EK, Clayton DB, Elliott MA. In vivo sodium MR imaging of the intervertebral disk at 4 T. Acad Radiol. 2002;9:800–4. doi: 10.1016/s1076-6332(03)80350-1. [DOI] [PubMed] [Google Scholar]
  • 11.Madelin G, Lee J-S, Regatte RR, Jerschow A. Sodium MRI: methods and applications. Prog Nucl Magn Reson Spectrosc. 2014;79:14–47. doi: 10.1016/j.pnmrs.2014.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Madelin G, Babb J, Babb J, Xia D, Chang G, Krasnokutsky S, Abramson SB, Jerschow A, Regatte RR. Articular cartilage: evaluation with fluid-suppressed 7. 0-T sodium MR imaging in subjects with and subjects without osteoarthriti. 2013;268:481–91. doi: 10.1148/radiol.13121511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Madelin G, Lee J-S, Inati S, Jerschow A, Regatte RR. Sodium inversion recovery MRI of the knee joint in vivo at 7T. J Magn Reson. 2010;207:42–52. doi: 10.1016/j.jmr.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Madelin G, Babb J, Babb J, Xia D, Chang G, Krasnokutsky S, Abramson SB, Jerschow A, Regatte RR. Articular cartilage: evaluation with fluid-suppressed 7. 0-T sodium MR imaging in subjects with and subjects without osteoarthriti. 2013;268:481–91. doi: 10.1148/radiol.13121511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Madelin G, Jerschow A, Regatte RR. Sodium relaxation times in the knee joint in vivo at 7T. NMR Biomed. 2012;25:530–7. doi: 10.1002/nbm.1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Eliav U, Keinan-Adamsky K, Navon G. A new method for suppressing the central transition in I=3/2 NMR spectra with a demonstration for 23Na in bovine articular cartilage. Journal of Magnetic Resonance. 2003;165(2):276–81. doi: 10.1016/j.jmr.2003.09.002. [DOI] [PubMed] [Google Scholar]
  • 17.Ling W, Regatte RR, Schweitzer ME, Jerschow A. Behavior of ordered sodium in enzymatically depleted cartilage tissue. Magn Reson Med. 2006;56(5):1151–5. doi: 10.1002/mrm.21062. [DOI] [PubMed] [Google Scholar]
  • 18.Borthakur A, Mellon E, Niyogi S, Witschey W, Kneeland JB, Reddy R. Sodium and T1ϱ MRI for molecular and diagnostic imaging of articular cartilage. NMR Biomed. 2006;19(7):781–821. doi: 10.1002/nbm.1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Keinan-Adamsky K, Shinar H, Shabat S, Brin YS, Nyska M, Navon G. 23Na and 2H magnetic resonance studies of osteoarthritic and osteoporotic articular cartilage. Magn Reson Med. 2010;64:653–61. doi: 10.1002/mrm.22479. [DOI] [PubMed] [Google Scholar]
  • 20.Lee J-S, Regatte RR, Jerschow A. Selective detection of ordered sodium signals by a jump-and-return pulse sequence. J Magn Reson. 2009;200(1):126–9. doi: 10.1016/j.jmr.2009.06.015. [DOI] [PubMed] [Google Scholar]
  • 21.Plateau P, Gueron M. Exchangeable proton NMR without base-line distortion, using new strong-pulse sequences. J Am Chem Soc. 1982;104:7310–1. doi: 10.1021/ja00389a067. [DOI] [Google Scholar]
  • 22.Hore PJ. Solvent suppression in Fourier transform nuclear magnetic resonance. J Magn Reson. 1983;55:283–300. doi: 10.1016/0022-2364(83)90240-8. [DOI] [Google Scholar]
  • 23.Sklenář V, Starčuk Z. 1-2-1 Pulse train: A new effective method of selective excitation for proton NMR in water. J Magn Reson. 1982;50:495–501. doi: 10.1016/0022-2364(82)90015-4. [DOI] [Google Scholar]
  • 24.Turner DL. Binomial solvent suppression. J Magn Reson. 1983;54:146–8. doi: 10.1016/0022-2364(83)90154-3. [DOI] [Google Scholar]
  • 25.Thomasson D, Purdy D, Finn JP. Phase-Modulated binomial RF pulses for fast spectrally-selective musculoskeletal imaging. Magn Reson Med. 1996;35:563–8. doi: 10.1002/mrm.1910350416. [DOI] [PubMed] [Google Scholar]
  • 26.Jerschow A. From nuclear structure to the quadrupolar NMR interaction and high-resolution spectroscopy. Prog Nucl Magn Reson Spectrosc. 2005;46:63–78. doi: 10.1016/j.pnmrs.2004.12.001. [DOI] [Google Scholar]
  • 27.Brown R, Brown R, Madelin G, Lattanzi R, Lattanzi R, Chang G, Regatte RR, Sodickson DK, Wiggins GC. Design of a nested eight-channel sodium and four-channel proton coil for 7T knee imaging. Magn Reson Med. 2013;70(1):259–68. doi: 10.1002/mrm.24432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Pipe JG, Zwart NR, Aboussouan EA, Robison RK, Devaraj A, Johnson KO. A new design and rationale for 3D orthogonally oversampled k-space trajectories. Magn Reson Med. 2011;66:1303–11. doi: 10.1002/mrm.22918. [DOI] [PubMed] [Google Scholar]
  • 29.Pipe JG, Menon P. Sampling density compensation in MRI: Rationale and an iterative numerical solution. Magn Reson Med. 1999;41:179–86. doi: 10.1002/(SICI)1522-2594(199901)41:1<179::AID-MRM25>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]
  • 30.Ernst RR, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Oxford: Clarendon; 1988. [Google Scholar]
  • 31.Moon CH, Kim J-H, Zhao T, Bae KT. Quantitative 23Na MRI of human knee cartilage using dual-tuned 1H/23Na transceiver array radiofrequency coil at 7 tesla. J. Magn. Reson. Imaging. 2013;38:1063–72. doi: 10.1002/jmri.24030. [DOI] [PubMed] [Google Scholar]
  • 32.Gnahm C, Nagel AM. Anatomically weighted second-order total variation reconstruction of 23Na MRI using prior information from 1H MRI. Neuroimage. 2015;105:452–61. doi: 10.1016/j.neuroimage.2014.11.006. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp figures

Supporting Figure S1. Slices from 23Na images of the right knee of a healthy volunteer. The slices in the leftmost column are from the reference scan, performed without the first pulse of the QJR sequence shown in Figure 1. The artery is indicated by yellow ovals. The other five columns present slices from the QJR scans with varying the delay tdelay, which is displayed at the top of each column.

Supporting Figure S2. Comparison of the normalized signal intensities between the QJR and IR scans for the six selected ROIs. In each scatter plot, a dotted line is drawn to show where the signal intensities between the QJR and IR scans are equal.

NIHMS923445-supplement-Supp_figures.docx (455.9KB, docx)

RESOURCES