Titration ELISA as a Method to Determine the Dissociation Constant of Receptor Ligand Interaction

Abstract

The dissociation constant describes the interaction between two partners in the binding equilibrium and is a measure of their affinity. It is a crucial parameter to compare different ligands, e.g., competitive inhibitors, protein isoforms and mutants, for their binding strength to a binding partner. Dissociation constants are determined by plotting concentrations of bound versus free ligand as binding curves. In contrast, titration curves, in which a signal that is proportional to the concentration of bound ligand is plotted against the total concentration of added ligand, are much easier to record. The signal can be detected spectroscopically and by enzyme-linked immunosorbent assay (ELISA). This is exemplified in a protocol for a titration ELISA that measures the binding of the snake venom-derived rhodocetin to its immobilized target domain of α2β1 integrin. Titration ELISAs are versatile and widely used. Any pair of interacting proteins can be used as immobilized receptor and soluble ligand, provided that both proteins are pure, and their concentrations are known. The difficulty so far has been to determine the dissociation constant from a titration curve. In this study, a mathematical function underlying titration curves is introduced. Without any error-prone graphical estimation of a saturation yield, this algorithm allows processing of the raw data (signal intensities at different concentrations of added ligand) directly by mathematical evaluation via non-linear regression. Thus, several titration curves can be recorded simultaneously and transformed into a set of characteristic parameters, among them the dissociation constant and the concentration of binding-active receptor, and they can be evaluated statistically. When combined with this algorithm, titration ELISAs gain the advantage of directly presenting the dissociation constant. Therefore, they may be used more efficiently in the future.

Download video file ^{(34.3MB, mp4)}

Introduction

The dissociation constant K is a key parameter to describe the affinity of a receptor (R) for its ligand (L). Based on the law of mass action, K is defined for the equilibrium, in which the receptor-ligand complex RL dissociates into the receptor R and the ligand L:

            Equation 1

with the indices f indicating the free/unbound state of receptor and ligand. The concentration of the receptor-ligand complex, RL, is identical to the concentration of the receptor-bound ligand Lb. As the total concentration of receptor Rt is the sum of the free receptor Rf and ligand-bound receptor Rb = Lb, the dissociation constant can also be written as:

        Equation 2

Therefore, the saturation yield Y, defined as the fraction of bound ligand Lb in relation of the total concentration of receptor Rt,

        Equation 3

depends on the concentration of free ligand Lf:

        Equation 4

This hyperbolic relation describes the binding curve of a receptor-ligand interaction and its plot shows the concentration of bound ligand Lb as a function of the concentration of free ligand Lf. From the binding curve, the dissociation constant K can be derived as the concentration of free ligand at half-maximal saturation yield. Moreover, different algorithms to linearize binding curves have been established, such as the double-reciprocal plot by Klotz1,2, or transformations according to Scatchard or Hanes (reviewed by Bisswanger3). However, all algorithms suffer from the problem that the maximum value of the saturation yield, which is asymptotically approached at high concentrations of free ligand in the binding curve, has to be estimated in a graphical pre-evaluation and therefore is error-prone.

In addition, the determination of a binding curve requires the quantification of free and bound ligand during the binding equilibrium. To this end, the free ligand has to be separated from the receptor-bound ligand and quantified. Therefore, the ligand and receptor have to differ in their properties, such as a non-protein ligand as opposed to a protein receptor. If both binding partners are proteins, they have to be distinguishable in their sizes, charges, or other molecular features. Nevertheless, the quantification of ligand concentrations in small-scale binding approaches is a difficult task. Radioactive labeling of the ligand has often been necessary to detect the low concentration of bound ligand, especially if substantial amounts of receptors were not available or affordable. Moreover, the receptor-bound ligand may dissociate during and after isolation in a non-negligible manner. Hence, complex methods, such as equilibrium gel filtration4, capillary electrophoresis5, and pulse proteolysis6, are required to quantify receptor-bound ligand and separate it from free ligand.

In contrast to these binding assays, titration experiments do not require the quantitative separation of bound and free ligand. To this end, a receptor at a constant concentration is titrated with different concentrations of added ligand. By binding to the receptor, the bound ligand has a biophysical property which distinguishes it from the free ligand and is measurable by, e.g., photometry, fluorometry, or antibody detection. Thus, a signal S, which is proportional to the saturation yield Y and consequently also to the concentration of receptor-bound ligand (Lb), is detected as a function of the total concentration of added ligand (Lt). Both parameters, the signal S and the total concentration of added ligand are quantified in a direct and easier manner than the concentrations of bound and free ligand. Especially, the detection of receptor-bound ligand by enzyme-linked immunosorbent assay (ELISA) allowed the reduction of sample volumes to below 100 µL as well as parallel measurements of several ligand concentrations in multi-well microtiter plates. In a titration ELISA, a receptor is physically adsorbed to a microtiter plate at the same concentration and titrated with soluble ligand. The receptor is immobilized to the plastic surface essentially by hydrophobic adsorption. The surface concentration of immobilized receptor correlates with the coating concentration of the receptor in a nonlinear relation, likely according to Langmuir´s adsorption isotherm7. In addition to the overall number of adsorbed receptor molecules, their activity state is another important parameter for titration assays. Only immobilized receptors which have retained ligand binding activity, are relevant for the titration assay and eventually contribute to the total concentration of active receptors Rt of the titration assay, which cannot be determined directly.

Sites on the plastic surface, which are not covered by the immobilized receptor are prone to adsorb other proteins, such as the ligand. Physical adsorption of the ligand to such plastic surface sites would result in a similar signal as the receptor-bound ligand, yet in a nonspecific manner. To reduce this nonspecific signal, the plastic surface sites of the microtiter plates which have not been coated with protein yet will be blocked with bovine serum albumin (BSA). However, for some receptor-ligand titration assays, nonspecific background signals may be observed. Then, other blocking agents, such as a solution of 0.2% gelatin or of 0.04% Tween 20, are recommended.

After binding to the receptor, the free ligand is removed by two washing steps. Bound ligand remains with the receptor, which is immobilized to the plastic surface of the microtiter well, and optionally reinforced by chemical fixation. For the subsequent covalent cross-linkage of bound ligand and immobilized receptor with glutaraldehyde, the buffer substance TRIS is replaced for HEPES, without any change in ligand binding. HEPES, in contrast to TRIS, does not inactivate glutaraldehyde. The covalent cross-linkage with glutaraldehyde fixes the bound ligand with its receptor and prevents its dissociation during subsequent washing and incubation steps. Thus, the receptor-ligand interaction is chemically frozen and warrants a titration curve which is unaffected by subsequent steps of washing and incubation. However, glutaraldehyde fixation may chemically modify the ligand and receptor in such a way that their interaction is reduced or abolished. Moreover, modification of epitopes within the ligand may change the binding affinity of the detecting antibody, especially if a monoclonal antibody is used to quantify bound ligand. Although neither of these adverse effects of glutaraldehyde fixation occurs in this titration ELISA, the sensitivity of the test towards glutaraldehyde must be tested for every receptor-ligand interaction prior to the titration experiment. After fixation, excess glutaraldehyde is removed in three washing steps with TRIS-containing buffer. TRIS inactivates remaining aldehyde groups, which might nonspecifically react with detecting antibodies in the subsequent step.

The amount of bound ligand is quantified with enzyme-linked antibodies, which provide a photometric ELISA signal S. This is plotted versus the total ligand concentration Lt added to each well. Despite its easier acquisition, the titration curve is not a hyperbolic function in contrast to the binding curve. Furthermore, it has been unclear how to calculate the dissociation constant K from a titration curve. Although algorithms to linearize spectroscopically acquired titration curves have been independently reported by Stockell8 and Heyn and Weischet9, they fell short due to their uncertainty of estimating the maximum signal value that the saturation yield approaches at high concentrations of added ligand.

Here, a titration ELISA and a non-linear regression algorithm are described to derive the dissociation constant K for a receptor ligand interaction from a titration curve. This protocol is exemplified for the interaction of the collagen-binding A-domain of the integrin α2β1 with a snake venom-derived inhibitor. Integrins are cell adhesion molecules, which mediate the anchorage of cells to the surrounding extracellular matrix or the underlying basement membrane10,11. Moreover, integrins convey important signals between cells and the extracellular matrix by recruiting additional signaling molecules and forming new cell organelles, adhesomes, upon cell-matrix interaction12,13,14. Collagen, the ligand of α2β1 integrin, is the most abundant protein of the human body and is a crucial scaffolding component of the connective tissue15. The interaction between α2β1 integrin and collagen is mediated by the A-domain of the integrin α2 subunit. The integrin α2A-domain contains a divalent cation, which is required for collagen binding and stabilizes its structure. The wild-type form as well as mutants of the α2A domain, such as the one in which the surface-exposed residue Y216 had been replaced for a glycine, can easily be produced recombinantly in a bacterial expression system and isolated via their oligo-His-tags with a NiNTA superflow column with a subsequent dialysis against TRIS-buffered saline (TBS; 50 mM TRIS/HCl, pH 7.4, 150 mM NaCl) containing 2 mM MgCl₂16. Their concentrations were determined with the bicinchoninic acid assay (BCA) and their purities are tested by conventional SDS-PAGE and stained with Coomassie-Brilliant Blue R250.

The interaction between α2β1 integrin and collagen is blocked by binding of the snake venom component, rhodocetin, from the Malayan pit viper (Calloselasma rhodostoma)16,17. Used as a soluble ligand in this titration ELISA, rhodocetin was purified from the crude venom as described previously16. It is dissolved in HEPES-buffered saline (HBS; 10 mM HEPES/NaOH, pH 7.4, 150 mM NaCl) and is stored frozen at -20 °C. Its concentration was determined by BCA and its purity was proven by SDS-PAGE. As an antagonist, rhodocetin not only blocks collagen binding to the integrin α2β1 A-domain, but also stabilizes the inactive conformation of the integrin thereby preventing any signaling from collagen into cells or platelets18. It is of great biomedical importance to determine the dissociation constant of rhodocetin with its receptor target and thus unravel its molecular mechanism and pharmaceutical potential e.g., as an antithrombotic agent. To this end, a titration ELISA is described including its evaluation, which is applicable to almost any receptor-ligand interaction with a 1:1 interaction stoichiometry.

Protocol

1. Stock Solutions

1. To prepare 100 mL of 10x TBS pH 7.4 solution, dissolve 6.06 g of TRIS and 8.77 g of NaCl in 90 mL of deionized water, adjust the pH to 7.4 with 37% HCl solution, fill the volume to 100 mL with deionized water, and filter the solution.

2. To prepare 100 mL of 1 M HEPES/NaOH, pH 7.4 solution, dissolve 23.83 g of HEPES in 90 mL of deionized water, adjust the pH to 7.4 with 1.5 M NaOH, fill the volume to 100 mL with deionized water, and filter the solution.

3. To prepare 100 mL of 5 M NaCl solution, dissolve 29.2 g of NaCl in 90 mL of deionized water. Fill the volume to 100 mL with deionized water and filter the solution.

4. To prepare 100 mL of 1 M MgCl₂ solution, dissolve 20.33 g of MgCl₂ · 6H₂O in 90 mL of deionized water. Fill the volume to 100 mL with deionized water and filter the solution.

5. To prepare 5% heat-inactivated BSA in water, weigh 2.5 g of BSA (fraction V, pH 7.0) in a 50 mL tube and dissolve it in 45 mL of deionized water. Fill the solution to 50 mL with deionized water, and heat the solution in a water bath at 68 °C for 45 min. Cool it in an ice bath and store it at -20 °C.

6. Prepare aqueous 25% glutaraldehyde solution. CAUTION: Glutaraldehyde is harmful if swallowed, toxic by inhalation, and causes burns. Wear protective clothing, gloves, and eye/face protection.

7. Raise the rabbit antiserum as previously described19. The titer of antiserum was determined according to standard protocols20.

8. Prepare anti-rabbit immunoglobulin-antibodies from goat conjugated with alkaline phosphatase.

9. To prepare 100 mL of 0.1 M glycine solution, dissolve 0.75 g of glycine in 90 mL of deionized water. Adjust the pH to 10.4 with 1.5 M NaOH solution, fill the volume to 100 mL with deionized water, and filter the solution.

10. To prepare 100 mL of 0.5 M Zn(II)-acetate solution, dissolve 10.98 g of Zn(II)-acetate · 2H₂O in 90 mL of deionized water. Fill the volume to 100 mL with deionized water and filter the solution.

11. To prepare 100 mL of 1.5 M NaOH solution, dissolve 6.0 g of NaOH in 90 mL of deionized water. Fill the volume to 100 mL with deionized water and filter the solution.

2. Prepare Buffers and Working Solutions

1. Dilute 5 mL of 10x TBS pH 7.4, with 45 mL deionized water and add 100 µL of a 1 M MgCl₂ stock solution. Keep it at room temperature. The TBS, pH 7.4, 2 mM MgCl₂ solution is for immobilization of the receptor and washing the microtiter plate.

2. Dilute 10 mL of 5% of heat-inactivated BSA in water and 5 mL of 10x TBS, pH 7.4 with deionized water to 50 mL. Add 100 µL of 1 M MgCl₂ stock solution and mix the solution well. Keep it on ice and store it for further experiments at -20 °C. Note that 2.5 mL of 1% BSA in TBS, pH 7.4, 2 mM MgCl₂ are required for each titration curve.

3. Dilute 2.5 mL of 1 M HEPES/NaOH, pH 7.4 and 1.5 mL 5 M NaCl solution to 50 mL with deionized water, add 100 µL 1 M MgCl₂ solution, and mix the solution thoroughly to prepare 50 mL of HBS, pH 7.4: 50 mM HEPES/NaOH, 150 mM NaCl.

4. Add 5 µL of 1M MgCl₂ stock solution and 2 µL 0.5 M Zn(II)-acetate stock solution to 5 mL 0.1 M glycine solution, pH 10.4 to prepare alkaline phosphatase (AP) buffer (0.1 M glycine solution, pH 10.4, 1 mM MgCl₂, 0.2 mM Zn(II)-acetate).

3. Immobilization of the Receptor (Integrin α2A-Domain) to a Microtiter Plate

1. Dilute the stock solution of integrin α2A-domain in TBS, pH 7.4, 2 mM MgCl₂ for a final concentration of 5 µg/mL. NOTE: The volume of the coating solution is 650 µL for one titration curve comprising a 12 well-row of a half area-microtiter plate.

2. Fill every well of a row on a half area-microtiter plate with 50 µL/well of the 5 µg/mL coating solution of integrin α2A-domain (wild-type or mutant). Perform every titration row at least in duplicates (in this example as quadruplets; see layout of microtiter plate in Figure 1).

3. Seal the plate with foil or close it with a lid. Leave the plate at 4 °C overnight.

4. Wash Coated Wells of the Plate Twice with TBS, pH 7.4, 2 mM MgCl₂

1. To remove soluble receptor molecules, which have not been immobilized to the plastic surface by physical adsorption, remove the coating solution and fill each well with 50 µL of TBS, pH 7.4, 2 mM MgCl₂.

2. Remove the wash solution. Ensure that the wells do not become dry. Therefore, do not tap the microtiter plate onto a tissue cloth to remove residual fluid. Use a multistep pipette or a multi-channel pipette to fill the wells quickly.

3. Repeat this washing step once.

5. Block Nonspecific Binding Sites

1. Add 50 µL of 1% BSA solution in TBS, pH 7.4, 2 mM MgCl₂ to each well.

2. Reseal the wells with foil or close with a lid.

3. Incubate the wells for 1 h at room temperature. NOTE: Any of the incubation steps of this protocol can be performed on a rocking or shaking platform. However, this is not required and does not alter the outcome of the experiment.

6. Preparation of a Serial Dilution Row of the Ligand, Rhodocetin

1. Vary the start concentration of rhodocetin and the dilution factor of the serial dilution, to obtain an appropriate range of ligand concentrations and to record a full titration curve with a minimum and maximum signal. In this experiment, employ a start concentration of 243 nM rhodocetin and a dilution factor of 2.3. Dilute the rhodocetin stock solution to the highest ligand concentration of the serial dilution row. For each titration curve with a dilution factor of 2.3, prepare 115 µL of 243 nM (i.e., 15,2 µg/mL) rhodocetin solution in 1% BSA/TBS, pH 7.4, 2 mM MgCl₂ in test tube #1.

2. Fill 65 µL of 1% BSA solution in TBS, pH 7.4, 2 mM MgCl₂ in 10 test tubes, labeled #2 through #11.

3. Transfer 50 µL of the rhodocetin dilution from test tube #1 to test tube #2, mix both solutions (total volume: 115 µL; dilution factor: 1:2.3) by trituration, and then transfer 50 µL from this mixture to test tube #3, etc.

4. Continue this serial dilution until test tube #11. NOTE: The volumes given in steps 6.1 - 6.4 are sufficient for one titration curve. Multiply these volumes by the number of replicates. In this case, perform eight titration curves (quadruplets of two α2A-domain forms) and prepare the following volumes: 920 µL of rhodocetin solution at the highest concentration in test tube #1; 520 µL of 1% BSA in TBS, pH 7.4, 2 mM MgCl₂ to fill in each of the test tubes #2 to #11; and 400 µL of transfer volume from one tube to the next one.

7. Binding of Ligand (Rhodocetin) at Different Concentrations to Immobilized Receptor (Integrin α2A-Domain)

1. Remove the blocking solution from the microtiter plate wells by a vacuum line.

2. Immediately add 50 µL of the rhodocetin solution in 1% BSA/TBS, pH 7.4/MgCl₂ solution of test tube #1 into wells of column 1, solution of test tube #2 to wells of column 2,etc. Add 50 µL of 1% BSA in TBS, pH 7.4, 2 mM MgCl₂ (blocking and dilution buffer) as a ligand-free control to wells of column 12 (see layout of microtiter plate, Figure 1).

3. Reseal the wells with foil or close with a lid.

4. Incubate the wells for 1.5 h at room temperature (around 20 - 22 °C).

8. Wash Wells of Plate Twice with HBS, pH 7.4, 2 mM MgCl₂

1. To remove non-bound ligand molecules, remove the binding solution and fill each well with 50 µL of HBS, pH 7.4, 2 mM MgCl₂. Then, remove the wash solution.

2. Take care that the wells do not become dry. Therefore, do not tap the microtiter plate onto a tissue cloth to remove residual fluid. Use a multistep pipette or a multi-channel pipette to fill the wells quickly.

3. Repeat this washing step once.

9. Fix the Receptor-bound Ligand with 2.5% Glutaraldehyde in HBS, pH 7.4, 2 mM MgCl₂

1. Prepare a fresh 2.5% glutaraldehyde solution by mixing 1 part of 25% glutaraldehyde solution and 9 parts of HBS, pH 7.4, 2 mM MgCl₂.

2. Fill every well of the microtiter plate with 50 µL of the 2.5% glutaraldehyde solution in HBS, pH 7.4, 2 mM MgCl₂. Incubate the microtiter plate for 10 min at room temperature.

10. Wash Wells of the Plate Three Times with 50 µL/well of TBS, pH 7.4, 2 mM MgCl₂

1. To remove and inactivate excess glutaraldehyde, remove the fixation solution and fill each well with 50 µL of TBS, pH 7.4, 2 mM MgCl₂. Then remove the wash solution. NOTE: Pour the glutaraldehyde-containing fixation solution from the microtiter plate into a dish and discard the fixation solution after it has been inactivated by an equal volume of TBS, pH 7.4.

2. Take care that the wells do not become dry. Therefore, do not tap the microtiter plate onto a tissue cloth to remove residual fluid. Use a multistep pipette or a multi-channel pipette to fill the wells quickly.

3. Repeat this washing step twice.

11. Quantification of Receptor-bound Ligand by ELISA

1. Add 50 µL/well of the primary antibody solution in 1% BSA in TBS, pH 7.4, 2 mM MgCl₂. The primary antibody solution is a rabbit antiserum raised against rhodocetin19, diluted 1:2,000 in 1% BSA in TBS, pH 7.4, 2 mM MgCl₂.

2. Incubate the plate for 75 - 90 min at room temperature. Wash all wells of the plate three times with 50 µL/well of TBS, pH 7.4, 2 mM MgCl₂. During the three washing steps, tapping of the microtiter plate onto a tissue cloth is not required.

3. Add 50 µL/well of the secondary antibody solution in 1% BSA in TBS, pH 7.4, 2 mM MgCl₂. To this end, dilute the secondary antibody, rabbit immunoglobulin-targeting goat antibodies conjugated with alkaline phosphatase, to 1:2,000 in 1% BSA in TBS, pH 7.4, 2 mM MgCl₂. Incubate the plate for 75 - 90 min at room temperature.

4. Prepare AP-detecting solution by dissolving a 5 mg tablet containing 4-nitrophenyl phosphate disodium salt hexahydrate (phosphatase substrate) in 5 mL of AP buffer (0.1 M glycine solution, pH 10.4, containing 1 mM MgCl₂ and 0.2 mM Zn(II)-acetate).

5. Wash all wells of plate three times with 50 µL/well of TBS, pH 7.4, 2 mM MgCl₂, immediately before performing the next step. Tap the microtiter plate onto a tissue cloth after the last washing step to remove all traces of liquid.

6. Add 50 µL/well of the AP-detecting solution to the wells of the microtiter plate. Add AP-detecting solution promptly to all wells to start the enzymatic conversion as simultaneously as possible. Therefore, use a multi-channel pipette.

7. Incubate the plate at room temperature until the solution in the wells with the highest ligand concentration turn yellow. NOTE: The incubation time may vary between 5 min and 1 h depending on the signal intensity.

8. Stop conversion of the phosphatase substrate by adding 50 µL/well of 1.5 M NaOH solution. Leave the plate standing for several minutes to ensure streak-free mixing of both solutions. To warrant the same incubation period in all wells, use a multi-channel pipette and add the 1.5 M NaOH in the same order added to the wells as that of the AP-detecting substrate in step 11.8.

9. Measure the optical density (OD) at 405 nm of each well by an ELISA reader.

12. Evaluation of the Titration Signals

1. Open the table of raw data, the OD_405nm values, with Excel. As these signal values of the titration curves are read in rows, transpose the values to a column and label with the concentrations of added ligand in another column.

2. Open the Graphpad Prism 5 (Version 5.0). Open a new project file in the main menu. Choose the XY format under New data & graph. Choose the option Enter and plot a single point for each value for the Y-axis.

3. Copy the two columns, concentration of added ligand and signal values (OD_405nm values) from the excel file and paste them into the data sheet of GraphPad Prism as X and Y values, respectively.

4. Open the Analysis sub-program of GraphPad Prism 5 and choose the option Non-linear regression under XY-analysis. Choose user-defined equation and press the New button to create a new equation.

5. Type the titration curve equation in the form: Y =(Smax-Smin)*((X+R+K)-sqrt((X+R+K)^2-4*R*X))/(2*R)+Smin + B*X into the newly opened template sheet, with Y being the signal value S, X being the concentration of added ligand L, R being the concentration of immobilized receptor, K being the dissociation constant, and B being the background slope. Define the appropriate constraints, such as K >0 and R >0. NOTE: This equation is the same equation of equation 9 in a different form.

6. Analyze the values of the data sheet by choosing the user-defined equation, which was newly created. Open the table with the calculated approximation values (K, Rt, Smax, Smin, and B) which are shown under the Result section on the left side of the software screen. NOTE: The software determines the 5 parameters by iterative fitting of the non-linear regression only if the titration curve consists of at least 5 data points.

7. Evaluate the parameters K, Rt, Smax, Smin, and B for every group of titration curves statistically, and correlate the parameters with the specific feature of the group (mutated or chemically-modified ligand or receptor).

Representative Results

After the ELISA has been developed, the yellow color of the converted alkaline phosphatase substrate, para-nitrophenolate, indicates that the amount of bound rhodocetin ligand decreases with decreasing concentrations of added rhodocetin from columns 1 to 11 (Figure 1). The colorless wells in the rhodocetin-free wells in column 12 show a low background signal.

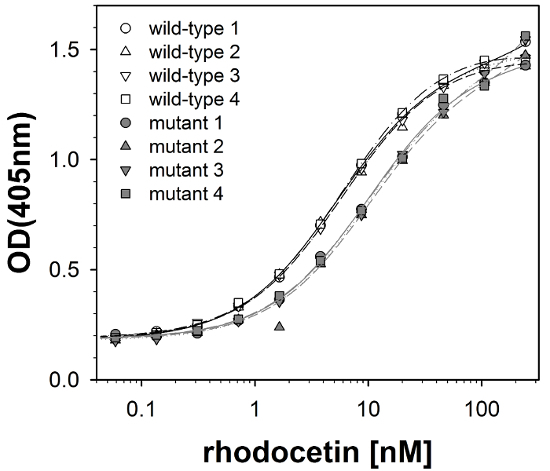
Photometric quantification at 405 nm provides data, which can directly be fed into an analysis software, and by using a non-linear regression and Equation 9, approximates the raw data of each titration row and calculates the signal S (which equals OD_405nm) as a function of the total concentration of added rhodocetin ligand Lt (Figure 2). The four titration curves for each receptor form (wild-type and mutant) are highly reproducible and almost superpose each other. In contrast to this low intra-group variance, the two groups of titration curves are clearly separated from each other. Higher concentrations of rhodocetin ligand are required for binding to the mutant α2A-domain to obtain signals of similar values to the ones of the wild-type form. This right shift of the titration curves demonstrates that the mutant ligand has a reduced affinity for the ligand. Thus, the mutation introduced into the α2A domain impairs rhodocetin binding because it is part of the rhodocetin binding site of the integrin domain18.

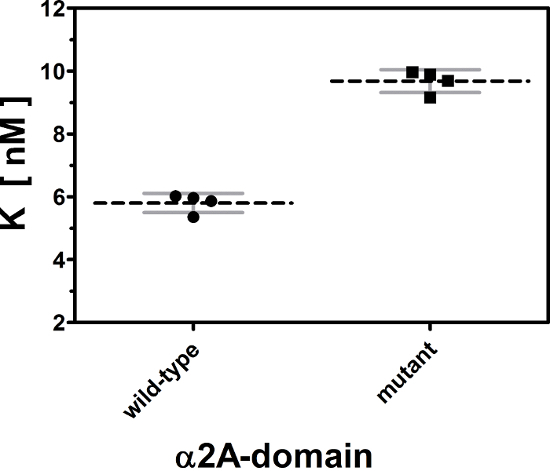
Titration curve can be described by 5 characteristic parameters: (i) dissociation constant K, (ii) concentration of immobilized, biologically active receptor Rt, (iii) maximum and (iv) minimum signals (Smax and Smin), as well as (v) the slope of the background signal B. Among these parameters, the dissociation constant K is essential and most pertinent for biological interpretation of titration curves. Every titration curve provides one value for K. Thus, single and also grouped titration curves can be statistically compared with each other. Such a statistical analysis of four titration curves for the wild-type and the mutated α2A-domain is shown in Figure 3. The affinity constant for the binding of rhodocetin to the wild-type α2A-domain is 5.80 ± 0.15 nM, whereas rhodocetin binds to the mutated receptor with a significantly lower affinity of 9.68 ± 0.18 nM (p <0.0001).

Thus, the titration ELISA together with this mathematical evaluation allows a fast and statistically sound evaluation of ligand binding to a receptor and its mutated or chemically modified derivatives. Therefore, both titration ELISA and the evaluation algorithm are valuable tools to analyze structure-function relations.

Figure 1: Representative layout of a microtiter plate for a titration ELISA. Each row provides the data for one titration curve. To compare their binding of rhodocetin (RC) ligand, wild-type (rows A-D) or mutant form (rows E-H) of α2A-domain are immobilized in wells of four rows each (quadruplet determination). The horizontal dot line separates the two groups of titration curves. The concentration of rhodocetin ligand decreases from column 1 to 11, while wells of column 12, indicated on the right side of the vertical dot line, do not contain any rhodocetin and represent the background control. The plate is shown after the bound ligand is quantified by ELISA in which the alkaline phosphatase substrate is converted to yellow para-nitrophenolate. Data are shown from one out of three repetitive experiments. Please click here to view a larger version of this figure.

Figure 2: Representative titration curves. The raw data of titrating immobilized wild-type and mutant forms of integrin α2A-domain with rhodocetin as soluble ligand (symbols), as well as the approximated titration curves (lines) are shown in a semi-logarithmic plot. Raw data of quadruplet determinations (circles, triangles up and down, squares for each of the four titration rows) are shown for immobilized wild-type (open symbols) and mutated (filled symbols) α2A-receptors. The calculated titration curves are shown as lines (solid, short dashed, dotted, chain-dotted) for the wild-type (black lines) and mutant (gray lines) form of the receptor. The four titration curves within each of the two groups (wild type and mutant receptor) superpose, whereas the titration curves clearly differ between the two groups. The titrations curves of the mutant α2A-domain are shifted to higher rhodocetin concentrations indicating that rhodocetin binds with lower affinity to the mutated receptor. Data are shown from one out of three repetitive experiments. Please click here to view a larger version of this figure.

Figure 3: Statistical comparison of dissociation constants K derived from titration curves. The dissociations constants of the eight titration curves from Figure 2 are plotted and grouped for the wild-type and mutant form of α2A domain. Individual values, group means, and standard deviations are indicated by points, by dashed black lines, and by gray error bars, respectively. The small variance within each group and the distinct difference between the group means demonstrate a significant difference (p <0.0001) in the affinity of the ligand to the wild type and to the mutant receptor. A two-tailed Student´s t-test was used for comparison. Data are shown from one out of three repetitive experiments. Please click here to view a larger version of this figure.

Discussion

The titration ELISA is a versatile test system to determine the dissociation of a receptor-ligand interaction. As the titration ELISA circumvents the necessity to separate free and bound ligands effectively and to analyze their concentrations quantitatively, substantially more studies and publications have employed titration ELISAs instead of recording binding curves. Moreover, titration ELISAs are easy to perform and require reasonably low amounts of receptor and ligand. For accurate analysis of dissociation constants, pure preparations of both receptor and ligand must be used. Contaminating proteins within the receptor preparation compete with the receptor for the adsorption sites on the plastic surface of the microtiter plate. As they do not bind ligand but reduce the number of ligand-binding receptors, impurities of the receptor solution reduce the signals of the titration ELISA. If the purity of the receptor preparation cannot be improved any further, an antibody directed against the receptor can be immobilized to the microtiter plate and, after blocking the wells, will capture the receptor from a preparation containing impurities. Nevertheless, care must be taken so that the capturing antibody does not disturb the detection of bound ligand with the primary and secondary antibodies because of species interferences of the antibodies, or that it hinders ligand binding.

To obtain a comprehensive set of data, it is appreciated to perform the titration ELISA in a reciprocal manner, which is to use the soluble ligand of one experiment as the receptor in the other experiment by immobilizing it to the microtiter plate and to titrate it with the former receptor which will be applied as the soluble ligand partner. This usually works well unless immobilization inactivates the binding activity of one of the partners or unless tools, such as antibodies to detect the titrated partner, do not exist or are difficult to obtain. In the rhodocetin-α2A domain binding system, this worked well after a glutathione-S-transferase (GST)-moiety was fused to the α2A-domain to facilitate its detection with GST-antibodies16.

Another advantage of the titration ELISA is that only the concentration of the added ligand (Lt), but not of the free and bound ligand (Lf and Lb, respectively), needs to be known. Therefore, the ligand preparation should be as clean as possible. If this is impossible or feasible only to a limited extent, the titration ELISA can still be employed, after the molar ratio of ligand within the preparation has been determined independently, e.g., by SDS-PAGE, immunoblotting, or sandwich ELISA.

Problems with the titration ELISA may occur if the affinity between the receptor and ligand is too low or if glutaraldehyde fixation abolishes the binding interaction. In the latter case, a fixation-free protocol of the titration ELISA needs to be established. Practically, dissociation constants can only be detected if the binding partners interact with reasonably high affinity, which is in the range of below approximately 200 nM.

The titration provides signal intensities S as a function of total concentrations of added ligand, Lt. As the concentrations of free and unbound ligands, Lf and Lb, sum up to Lt, and as Lb equals the product of Y·Rt according to Equation 3, Equation 4 is transformed to:

          Equation 5

resulting in the quadratic equation,

        Equation 6

whose practical solution is,

        Equation 7

In addition, the signal intensity S(Lt) at a specific concentration of added ligand Lt represents the saturation yield Y, after it has been corrected by subtraction of the minimum signal value, Smin, and normalized to the dynamic range, given as the difference between maximum and minimum signal values, Smax and Smin:

          Equation 8

The combination of Equation 7 and Equation 8 yields the mathematical function which correlates the signal intensity S(Lt) with the concentration of added ligand Lt. A term B·Lt can be added to describe the nonspecific background signal which linearly raises with Lt. B is the proportionality constant of the background. Thus, the general function to describe a titration curve is:

        Equation 9

This function of a titration curve corresponds to a composed function with a square root term and a linear term, which describe the specific interaction between the receptor and ligand and the nonspecific interactions of ligand, respectively. This function is different from the hyperbolic function of the binding curve (Lbvs. Lf).

In contrast to the binding curve, in which the concentrations of bound ligand is plotted on the y-axis, the titration curve is more flexible and allows any signal, which correlates with the concentration of bound ligand, to be plotted on the y-axis. This signal could be the photometrically detected binding of an enzyme-linked antibody (as in this case of an ELISA), but it could also be other spectrometric signals, such as a change in absorbance, circular dichroism9, fluorescence polarization21, and NMR signals22. Moreover, also thermodynamic signals from isothermal titration calorimetry23 should be possible to be evaluated. Other studies determine the binding affinity from the kinetic on- and off rates for the formation and dissociation of the receptor-ligand complex by measuring real-time changes in the evanescent field by surface plasmon resonance24,25, in mass deposition by a quartz crystal microbalance26, or in fluorescence by microscale thermophoresis26,27. These real-time measurements have become powerful tools because of their sophisticated evaluation software. Titration ELISA and SPR are generally the method of choice to examine binding partners in protein-chemical analysis. Whereas titration ELISA measures the affinity constant thermodynamically by quantifying the amount of bound ligand at different equilibrium states, SPR utilizes a kinetic approach and approximates the kinetic rate constants, k_off and k_on, the ratio of which provides the kinetically determined dissociation constant24,25. Depending on the two different approaches, the K values may differ from each other. In the rhodocetin-α2A domain binding experiments, the SPR data revealed k_off and k_on rate constants, and consequently a kinetically determine affinity constant K, for the rhodocetin-α2A complex19, which are very similar to the K-values measured in this study by titration ELISA. Slight differences can be explained by activity variations of different batches or different conditions and durations of storage of the protein samples. In this later respect, in the titration ELISA all samples are measured simultaneously and not sequentially like in the SPR machine. Now, being mathematically accessible and easy to manage with the titration curve equation (Equation 9), this end-point measurement of the titration ELISA might become just as powerful as the kinetically evaluated real-time measurements, which require a cost-intensive SPR machine.

This equation takes into account that the total concentration of ligand is reduced by the concentration of bound ligand, especially at low ligand concentrations. This allows much better approximations of the titration curve to the data over the entire range of ligand concentrations. One drawback of the titration ELISA, as compared to the binding curve, has so far been the difficulty to mathematically evaluate the titration curve. Whereas in a binding curve the concentration of free ligand Lf at half-maximal saturation equals the dissociation constant, this is not true for a titration curve. Two algorithms have been independently developed to graphically linearize titration curves and to determine the dissociation constant. However, both algorithms developed for spectroscopic titration experiments by Stockell et al.8 and by Heyn & Weischet9 suffer from the disadvantage that the maximum signal for the saturation yield Y must be determined graphically. As this value is approached asymptotically, the saturation yield and consequently the calculated dissociation constant are intrinsically error prone. In contrast, the algorithm based on Equation 9 uses raw data from titration experiments and calculates the dissociation constant K as well as other parameters in a non-linear regression to find the best-fit solution (Figure 2 and Figure 3). Moreover, as this algorithm does not need to graphically estimate the possibly out-reaching maximum signal at ligand saturation, the evaluation process becomes much faster and accurate and it bears less bias than the graphical evaluation. Several titration curves can be evaluated in parallel. Thus, several groups of titration curves can be measured simultaneously, and their parameters can be statistically analyzed and compared. Moreover, every titration curve gives a set of values, among them the dissociation constant K, concentration of immobilized and binding-active receptor Rt, the dynamic range as difference of maximum and minimum signal values Smax and Smin, as well as the linear factor B which corresponds to the experimental background signal Using these values, the saturation yield Y can be calculated and plotted in dependence of the concentration of added ligand Lt. In such a saturation yield plot, the concentration of the added ligand at half-maximal saturation signal Lt(50%) equals the sum of the dissociation constant K plus half the concentration of immobilized active receptor Rt

        Equation 10

This can be derived for Y = 0.5 with Equation 7. Thus, the concentration of immobilized active receptor Rt can be determined by performing the titration ELISA with different coating concentrations of the receptor.

Disclosures

The author has nothing to disclose.