Mining the Synergistic Core Allosteric Modules Variation and Sequencing Pharmacological Module Drivers in a Preclinical Model of Ischemia

Abstract

Identifying the variation of core modules and hubs seems to be critical for characterizing variable pharmacological mechanisms based on topological alteration of disease networks. We first identified a total of eight core modules by using an approach of multiple modular characteristic fusing (MMCF) from different targeted networks in ischemic mice. Interestingly, the value of module disturbance intensity (MDI) increased in drug combination group. Second, we redefined a weak allosteric module and a strong allosteric module. Then, we identified 15 pharmacological module drivers (PMDs) by leave‐one‐out screening with a cutoff of two folds, which were at least, in part, validated by expression and variation of topological contribution. Finally, we revealed the fusional and emergent variation of PMD in core modules contributing to multidimensional synergistic mechanism in ischemic mice and rats. Our findings provide a new set of drivers that might promote the pharmacological modular flexibility and offer a potential avenue for disease treatment.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Identifying the variation of core modules and hubs seems to be critical for characterizing variable pharmacological mechanisms based on topological alteration of disease networks.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study first identified the core modules by using an approach of MMCF from different targeted networks in cerebral ischemia. We redefined a weak allosteric module and a strong allosteric module. Then, we identified the PMDs.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ This study reveals the diversity of fusional and emergent variations of PMD in core modules contributing to multidimensional synergistic mechanism in ischemic mice.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS

☑ This study provides a new set of drivers that might promote the pharmacological modular flexibility and offers a potential avenue for disease treatment.

Dissection of variable mechanisms of drug combination is still challenging due to complex molecular evolution processes that may be associated with pathophysiological and pharmacological changes. Modular structure plays a significant role in aiding the diagnosis, prevention, and therapeutic treatment of diseases.1 To date, hundreds of methods have been proposed for module identification,2 which may help us to elucidate how various deciphering mechanisms operate to ensure precise module identification and assembly.3 Generally, the multipotent functional changes in modular architecture are referred to as allosteric modules,4 which can be used to reflect the dynamics of modular networks and quantitatively analyze allosteric variations to reveal detailed allosteric pharmacological events in cellular networks.5 Modular pharmacology suggests that the treatment of complex diseases requires a modular design to affect multiple targets. The modular pharmacology extends the comprehension of drug targets from entitative ontology to relational ontology,6 which may help to measure and integrate the multipart relationship between drug and disease. Thus, dynamic variation of core modules and key hubs may satisfy the modified heterogeneity of biological networks – criteria for judging whether a specific network member can provide an important impetus for network evolution – for causality of systematic regulation.

Although searching for the dominant region in enormous information dataset is not an easy task, the opening work is still concentrated in finding the leader of numerous modules. For example, knowledge‐driven matrix factorization aims at calculating the value of interaction between modules through module matrix and network structure matrix, and a higher value of the module indicates a more important position.7 In another study, researchers developed a pathway‐based tool entitled COre Module Biomarker Identification with Network ExploRation (COMBINER), and assumed that core modules might consist of driver genes and their first‐degree neighbors.8 Additionally, researchers also focused on the overlapping modules and root‐like upstream based on multiple specific stress regulator modules and a graphical approach derived from the dynamical laws, respectively,9, 10 It seems that network modules are artificially divided into domination and subordination, and a core module is defined as a unit occupying the leading architecture and dominating function. However, what we attempt to do is not only quantitatively identifying core modules and key hubs, but also discussing the dynamic structural changes of these core modules based on pharmacological module drivers (PMDs). We define PMD as an actual component entity of a module that has the ability to drive the conformation of this module. This is not only a huge challenge for deeply understanding the evolutional instant of key factors in biological system, but also an opportunity for further characterizing the synergistic mechanism of drug combination. Thus, we developed a new approach named Quantitative Core Module and Driver Paradigm, which may contribute to translational medicine in a practical and real‐world manner. Remarkably, as a pharmacological mechanism model, Qingkailing injection with two bioactive components of jasminoidin (JA) and ursodeoxycholic acid (UA), which are commonly used for treating cerebral ischemia, has been extensively studied in both basic and clinical experiments during the last few years,11, 12, 13 which is considered an indispensable precondition for scanning the context of intermolecular cooperation frame by frame.

MATERIALS AND METHODS

In this study, we administered the interventions of geniposide alone, cholic acid alone, and their combination in middle cerebral artery occlusion (MCAO) models, built networks based on the different genes of gene microarrays, and identified the core modules from these networks by using the approach of multiple modular characteristic fusing (MMCF). Then, the spectrum of adjacency matrix was used for identifying PMDs, which were also validated by topological contributions, animal experiments, published literature, and available databases.

Molecular network mapping

Animal models control and pharmaceutical administration were strictly executed. The differentially expressed genes identified by microarray analysis consisted of 11,644 cDNAs. One‐way analysis of variance models and significance analyses of microarrays were used to compare the means of the altered genes between groups.11, 12 A total of 414, 470, and 401 significantly differentially expressed genes were found among JA vs. vehicle, UA vs. vehicle, and JU (jasminoidin and ursodeoxycholic acid) vs. vehicle, respectively. Then, all the significantly differentially expressed genes in each group were uploaded to the ingenuity pathway analysis system (http://www.ingenuity.com/). A cutoff was set to identify molecules whose expression was significantly differentially regulated. All the protein molecules with specific semantic annotations were filtrated out, and were able to attract out all the rest of the molecules from the STRING database (http://www.string-db.org/) to construct networks. A strategy extracting the multiscale backbone of complex weighted networks was used.14 The method offers a practical procedure to extract the relevant connection backbone in complex multiscale networks, thereby preserving the edges that represent statistically significant deviations with respect to a null model for the local assignment of weights to edges. It does not belittle small‐scale interactions and operates at all scales defined by the weight distribution. The multiscale backbone has between‐edge weight scales ranging from 0–1, which depends on eight aspects of evaluation on intermolecular interaction coefficient in the STRING database (i.e., neighborhood, gene fusion, co‐occurrence, co‐expression, experiments, databases, text‐mining, and homology). When we got this weighted network skeleton, second‐order neighbors were merely reserved around those “baits” of each group to limit the spread range of activity and further form the targeted network.

Modular screening and stability

Three module‐screening methods, including affinity propagation (AP; parameters: lambda parameter = 0.5, number of iterations = 8),15 Markov Cluster algorithm (MCL; parameters: granularity parameter = 2.0, number of iterations = 16),16 and Molecular Complex Detection (MCODE; parameters: degree cutoff = 2, K‐core = 2, and node score threshold = 0.2),17 were compared. The AP takes as input measures of similarity between pairs of data points, and real‐valued messages are exchanged between data points until a high‐quality set of exemplars and corresponding clusters gradually emerges. The MCL algorithm assigns proteins into families based on precomputed sequence similarity information. The MCODE is based on vertex weighting by local neighborhood density and outward traversal from a locally dense seed protein to isolate the dense regions according to given parameters. Their network structure entropies were calculated for balancing the selective speculation.18 Network structure entropy is defined as follows:

$$E=-{\displaystyle \sum _{i=1}^N{I}_i}\ln \hspace{0.17em}Ii$$ (1)

where N is the number of nodes in network, and I_i is the importance of node i. A smaller entropy value means higher similarity between modular nodes, thereby determining module stability.

Core module identification using the multiple modular characteristic fusing approach

In this network, modules were regarded as “super‐nodes,” and the weighted edges between these modules were derived from the intermolecular relations across modules. The approaches of multiple modular characteristic fusing (MMCF), including weighted degree,19 betweenness centrality,20 and PageRank,21 were used for this searching process.

We removed each core module from the whole network and the module network, respectively, and then observed the rate change of the characteristic path length L22 to validate the results of identification.

$$L=\frac{1}{\mathrm{n}}{\displaystyle \sum _{i\in N}{L}_i=}\frac{1}{n}{\displaystyle \sum _{i\in N}\frac{{\displaystyle {\sum }_{j\in N.j\ne i}{d}_{ij}}}{n-1}}$$ (2)

where i and j are the different nodes in the network, $L_{\mathrm{i}}$ is the average distance between node i and all other nodes, and d_ij is the distance between node i and j.

GO functional enrichment analysis

The DAVID version 6.7 (http://david.abcc.ncifcrf.gov/) software was used for functional enrichment analysis, with species restricted to Mus musculus. The biological process and Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway are able to describe the biological features of modules. Modified Fisher's exact test and Benjamini were utilized for calculating and correcting P values (P < 0.05).

Calculation of module disturbances intensity

Module disturbance intensity (MDI) is used to characterize the degree of module fragmentation after being disturbed. Specifically, we got the formula of MDI for a given module with two variables – module disturbance and node disturbance. For any given module M, its MDI is defined as:

$$MDI=\frac{1}{2}\left(\frac{\left|M_D\right|}{\left|M_{D-\text{max}}\right|}+\frac{\left|N_{D-all}\right|-\left|N_D\right|}{\left|N_{D-all}\right|}\right)0<\text{MDI}<1$$ (3)

where M_D is a disturbing module set defined as M_D = {M_d |M ∩ M_d≠φ}, in other words, module M is dissociated into multiple modules M_d with intersecting disturbance nodes for tracing and confirming M_d. This means all modules in M_D can be the next state of module M after M is disturbed. When the theoretical members in M_D tend to be the most, we use M_D‐max instead of M_D, and the ratio of |M_D| to |M_D‐max| can be used to assess the disturbance of M in the module level based on reality and theory. The |M_D| represents the number of modules in M_D, M_D‐max = {M_d′|M∩M_d′≠φ, T_Md′→max}, and |M_D‐max| means the number of modules in the set M_D‐max. The same importance as module disturbance, node disturbance is another variable of MDI, which is still a ratio, only at node level within the module scale. Here, N_D is a node set, in which each node comes from M_d and must be the conservative member of the module M at the same time. In truth, we need to note the remaining nodes in M_d, because they are responsible for performing module phase change from M to M_d. As a result, the number ratio of the remaining nodes to all nodes in M_d is implied to express the degree of node disturbance. The N_D = {N_d |N_d∈M, N_d∈M_d}, N_D‐all = {N_d‐all |N_d‐all∈M_d}. The |N_D‐all| and |N_D| represent the number of nodes in N_D‐all and N_D, respectively.

Calculation of relative retention index and relative generation index

Relative retention index (RRI) refers to the number of unchanged nodes and edges of a module after drug combination divided by the total number of nodes and edges; and relative generation index (RGI) refers to the number of new nodes and edges of a module after drug combination divided by the total number of nodes and edges.

$$RRI=\frac{\left|N_R\right|+\left|E_R\right|}{\left|N_{New}\right|+\left|E_{New}\right|}$$ (4)

$$RGI=1-\frac{\left|N_R\right|+\left|E_R\right|}{\left|N_{New}\right|+\left|E_{New}\right|}$$ (5)

where $\left|N_R\right|=\left\{N_r|N_r\in M_{New,}{N}_r\in M_{old}\right\},\left|E_R\right|=\left\{E_r|E_r\in M_{New,}{E}_r\in M_{old}\right\}$ _, $\left|N_{New}\right|$ and $\left|E_{New}\right|$ are the number of nodes and edges in the drug combination group, respectively; $\left|N_R\right|$ and $\left|E_R\right|$ are the number of overlapping nodes and edges before and after drug combination, respectively; and $M_{{}_{Old}}$ and $M_{New}$ are the modules before and after the drug combination, respectively.

Identification of PMDs

We identified PMDs by leave‐one‐out screening and with a cutoff of two folds. A method using the spectrum of adjacency matrix was used for identifying PMDs.23 According to the normal distribution test, if it is a normal distribution, two times of the mean is considered as threshold; if it is an abnormal distribution, then two times of the median is considered as threshold. The eigenvalue of PMDs must equal or exceed the threshold of the dataset. Furthermore, for each PMD, we also calculated the topological contribution using the weighted degree, PageRank, and betweenness centrality of the network, so as to identify the importance of PMDs for the module from different points of view.

Western blotting

The expression levels of interleukin‐1 receptor antagonist (IL‐1RA) and CYCLIN were assessed by Western blotting analysis. The hippocampuses of three rats from each group were removed from the brains at 24 hours after ischemia. After cell lysis, 40 mg of protein were electrophoresed in 10% SDS‐polyacrylamide gels and transferred to polyvinylidene difluoride membranes.

Then, the primary and secondary antibodies rabbit anti‐IL1RA (Abcam, ab124962), mouse anti‐cyclin E1 (CST, 4129), and mouse anti‐b‐actin (Tiandeyue, Beijing, China) were used. Image analysis of the blots was performed on optical density‐calibrated images. The IL1RA and CYCLIN protein expression levels were normalized to b‐actin protein expression levels. Each measurement was performed in three replicates.

Real‐time polymerase chain reaction analysis

The changes in the expression of IGF1 was further validated by SYBR Green I real‐time polymerase chain reaction (PCR). Three rats from each group were used for this analysis. The total RNA of tissue samples was extracted by an ultrapure RNA extraction kit in accordance with the product instructions (CWbio, catalog #CW0581). We utilized 5μl RNA 1% agarose gel electrophoresis to detect the integrity of the RNA, and then used DNase I kit (CWbio, catalog #CW2090) and HiFi‐MMLVcDNA first strand synthesis kit (CWbio, catalog #CW0744) to digest residual genomic DNA in RNA and reverse transcription, respectively. The expression level was measured by quantitative real‐time PCR running on the ABI 7500 system following the product instructions. Relative quantitative data was calculated by the comparative Ct method (2‐^△△CT).24

RESULTS

According to our previous study,12 the combination of JA and UA showed a pharmacodynamic synergistic effect in fighting against cerebral ischemia. Figure 1 a illustrates the workflow of our proposed framework in analyzing the pharmacological mechanism. The significantly differentially expressed genes in JA, UA, and combination groups after intervention in MCAO models were identified through secondary screening of the microarray experiment and the ingenuity pathway analysis database. The molecules were mapped to the STRING database to construct the molecular networks via interaction between molecules and their first‐neighbor, and then the modules were identified from the network. Based on the edge of the nodes between the modules, the weighted module interaction network was constructed. The core module identification was implemented using the approach of MMCF, including weighted degree, betweenness centrality, and PageRank. For the core module, the spectrum of adjacency matrix was used for identifying PMDs by leave‐one‐out screening and with a cutoff of two folds, which were also validated, at least in part, by the variation of topological contribution.

Figure 1.

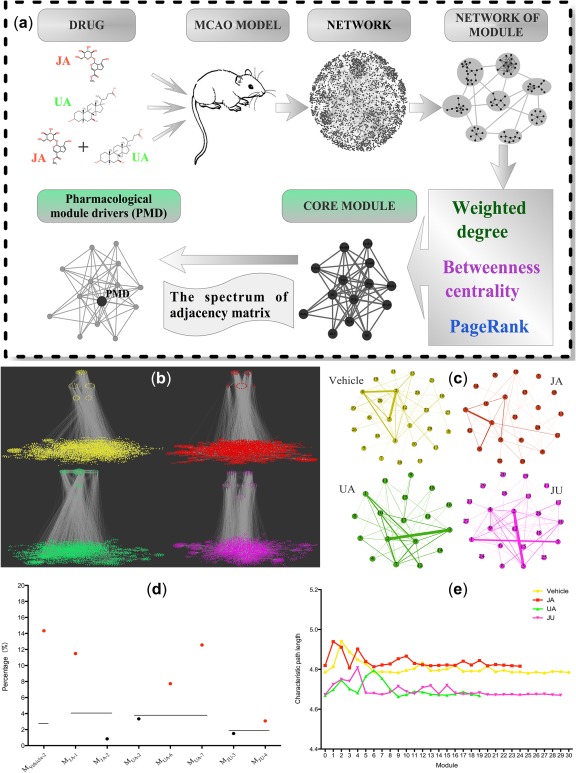
Schematic diagram of analyzing the synergistic pharmacological mechanism. (a) Workflow of identifying the pharmacological module driver (PMD). (b) Screening and identification of core modules from different ischemia networks. Networks in colors of yellow, red, green, and pink represent the vehicle, jasminoidin (JA), ursodeoxycholic acid (UA), and JU (jasminoidin and ursodeoxycholic acid) groups, respectively. The modules from top to down are the top three ranked modules identified by the three methods. (c) Modular network of each group; the nodes in the network represent modules. (d) The rate change of characteristic path length after removing each top one module identified by the three methods from the modular network. The black line is the average rate change of characteristic path length, and the red and black points represent longer or shorter than the average, respectively. (e) The characteristic path length after removing each module from the network. MCAO, middle cerebral artery occlusion.

Network mapping and module identification

The networks of the vehicle, JA, UA, and JU groups were listed, G_Vehicle: N = 3,750, E = 9,162; G_JA: N = 3,416, E = 7,581; G_UA: N = 3,407, E = 9,057; and G_JU: N = 3,429, E = 8,111 (Supplementary Figure S1a–d). According to the minimum entropy criterion, compared with two other methods (AP and MCL), MCODE demonstrated its strikingly consistent stability in each group (Table 1). Correspondingly, 30, 24, 19, and 29 modules were dug out from the network data of the vehicle, JA, UA, and JU groups, respectively (Supplementary Figure S2 and Supplementary Table S1).

Table 1.

Network structure entropy by different modular analysis methods and a list of the top three core modules screened by MMCF in each group

	Vehicle		JA		UA		JU
AP	7.0619		6.97052		6.9835		6.99358
MCL	7.47127		7.33767		7.22118		7.37138
MCODE	5.5791		4.78964		5.19916		5.09114
Weighted degree	Rank 1	2 (25.100)	Rank 1	1 (11.500)	Rank 1	2 (19.600)	Rank 1	3 (16.000)
	Rank 2	4 (15.900)	Rank 2	5 (8.100)	Rank 2	3 (17.200)	Rank 2	2 (15.600)
	Rank 3	5 (14.300)	Rank 3	2 (4.500)	Rank 3	6 (16.000)	Rank 3	1 (9.000)
Betweenness centrality	Rank 1	2 (254.946)	Rank 1	1 (156.533)	Rank 1	7 (114.538)	Rank 1	4 (101.167)
	Rank 2	3 (148.407)	Rank 2	21 (114.000)	Rank 2	6 (60.838)	Rank 2	10 (95.667)
	Rank 3	11 (105.800)	Rank 3	2 (96.383)	Rank 3	17 (60.000)	Rank 3	12 (67.900)
PageRank	Rank 1	2 (0.107)	Rank 1	2 (0.099)	Rank 1	6 (0.116)	Rank 1	4 (0.097)
	Rank 2	3 (0.800)	Rank 2	9 (0.094)	Rank 2	7 (0.110)	Rank 2	12 (0.084)
	Rank 3	5 (0.069)	Rank 3	1 (0.088)	Rank 3	2 (0.089)	Rank 3	10 (0.078)

Notes: The second to the fourth rows of the table are the results of network structure entropy using different methods; and the fifth to the seventh rows present the top three values by the three methods to identify the core modules. The figures listed are the module number and the score calculated from each method (in parentheses). All data are rounded to the third decimal place.

AP, affinity propagation; JA, jasminoidin; JU, jasminoidin and ursodeoxycholic acid; MCL, Markov Cluster algorithm; MCODE, Molecular Complex Detection; MMCF, multiple modular characteristic fusing; UA, ursodeoxycholic acid.

Identification and validation of core modules

Intermolecular relationships between modules can make the modules connect together (Figure 1 b). The modular networks of each group were displayed: G′_Vehicle: N = 27, E = 76; G′_JA: N = 22, E = 40; G′_UA: N = 18, E = 46; and G′_JU: N = 24, E = 72 (Figure 1 c). The top three modules with their scores confirmed by the three methods in each group are listed in Table 1 and shown in Figure 1 b. Finally, 1, 2, 3, and 2 highest‐ranked modules were identified as core modules in the vehicle, JA, UA, and JU groups, respectively (Table 1).

After removing the top one module identified by the three methods in each group from the modular network, five modules were found to have a higher‐than‐average rate change of the characteristic path length (Figure 1 d). Then, after removing each module one by one in each group from the global network, we observed that removing the top one module of each group had more effects on the global network (Figure 1 e).

Functional enrichment analysis of core modules

A total of 168, 248, 275, and 149 biological processes were detected from M_Vehicle‐2, M_JA‐1&2, M_UA‐2&6&7, and M_JU‐3&4, respectively (Figure 2 a, Supplementary Table S2). All of these biological processes could be divided into 17 categories (Figure 2 b, Supplementary Figure S3). The 30 unique functions in the JU group were shown to be associated with cerebral ischemia in previous studies (Supplementary Table S3).

Figure 2.

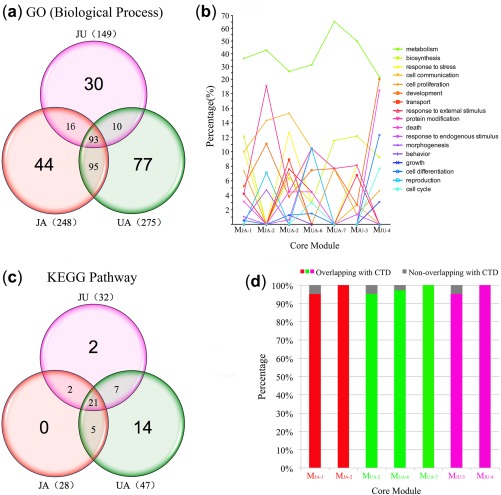
(a) The functional distribution and related pathways of all core modules. The number of biological processes in the jasminoidin (JA), ursodeoxycholic acid (UA), and JU (jasminoidin and ursodeoxycholic acid) groups. (b) Functional classification of each core module. (c) The number of Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways in the JA, UA, and JU groups. (d) Pathways of core modules match with cerebral ischemia‐related pathways in the Comparative Toxicogenomics Database (CTD); the colorful and gray histograms represent overlapping or nonoverlapping modules, respectively.

Moreover, 21, 28, 47, and 32 KEGG pathways were identified from M_Vehicle‐2, M_JA‐1&2, M_UA‐2&6&7, and M_JU‐3&4, respectively (Figure 2 c, Supplementary Table S4). Over 90% of KEGG pathways identified in each group were overlapped with those in the Comparative Toxicogenomics Database that were related with brain ischemia, infarction, middle cerebral artery, and cerebral infarction (Figure 2 d). Two nonoverlapping pathways (p53 signaling pathway and oocyte meiosis) were enriched in M_JU‐4. According to the published literature, most signaling pathways of drug groups were closely associated with cerebral ischemia. The top 10 biological processes and KEGG pathways are listed in Supplementary Table S5.

Variation of module disturbances intensity

As shown in Figure 3, with the spatiotemporal state migration, the originally pathological module was dismembered. Those dissociated fragments (red, green, and pink nodes) entered into multiple pharmacological modules to become positively responsive members in different drug groups (Figure 3b ₁ –d₅). Our data showed that the JU group experienced more powerful disturbances when overturning the pathological core module (MDI = 0.4332) than the JA (MDI = 0.3918) and UA (MDI = 0.3594) groups (Figure 3).

Figure 3.

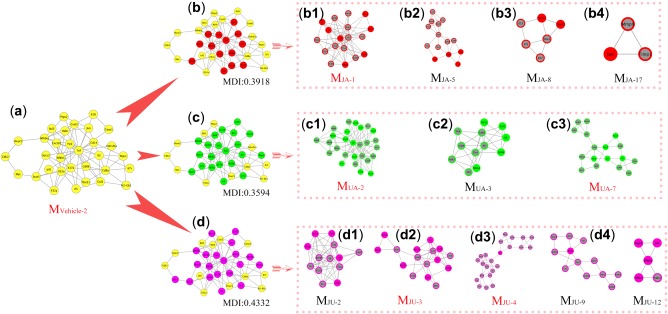
The dynamic images of divergence and convergence of core modules. (a) The core module of the vehicle group. It is divided by different modules in the jasminoidin (JA) (b; b1–b4), ursodeoxycholic acid (UA) (c; c1–c3), and JU (jasminoidin and ursodeoxycholic acid) (d; d1–d5) groups, including core modules (name in red) and other modules (name in black).

Relative retention index and relative generation index of core modules in the combination group

We plotted out the images of multiple core modules in the three drug groups and merged them into a geographic map (Figure 4 a). The map was artificially divided into two regions around the core modules of the JU group. One was composed of three overlapping modules (i.e., M_JU‐3 & M_JA‐1 & M_UA‐2) and the other consisted of two overlapping modules (i.e., M_JU‐4 & M_JA‐2). The two regions might be separated if no jointed nodes came from the M_UA‐6 and M_UA‐7.

Figure 4.

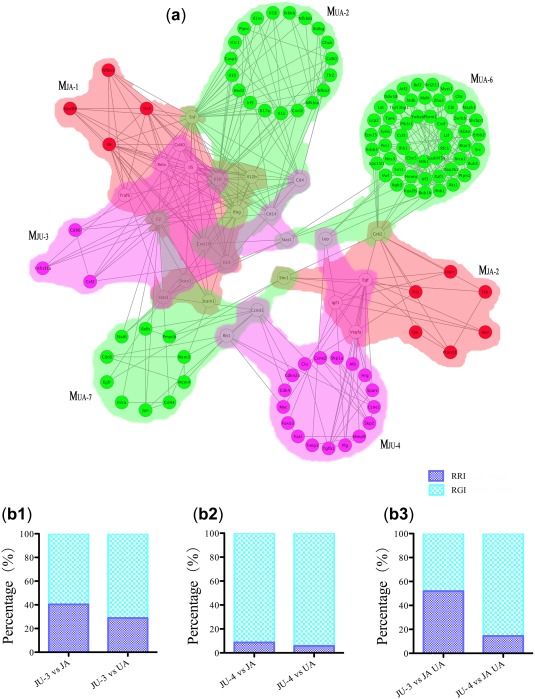
The detailed path of core modules and quantitative analysis of their alterations. (a) The relationship between core modules before or after drug combination. The red, green, and pink represent the jasminoidin (JA), ursodeoxycholic acid (UA), and JU (jasminoidin and ursodeoxycholic acid) groups, respectively. (b) The relative retention index (RRI) and relative generation index (RGI) of core modules in the combination group are compared with those in the monotherapy groups.

We used RRI and RGI to evaluate the change in the modular structure before and after the drug combination (Figure 4 b). In the drug combination group, M_JU‐3 was considered a weak allosteric module, because most (13/16) of its nodes were inherited from the core modules of the monotherapy groups, which might function to maintain metastable biological processes. Conversely, M_JU‐4 showed a strong allosteric tendency due to the presentation of more molecular newcomers.

Identification of PMDs and driver‐induced divergent core modules

In light of the abnormal distribution of eigenvalue set in each module, we hypothesized that the eigenvalue of PMDs should be at least two folds of the median of the dataset. The eigenvalue of PMDs must satisfy two qualifications: (1) it must rank first in each eigenvalue set; and (2) it must exceed the threshold of the dataset (Supplementary Figure S4). Finally, the PMDs of the core module of M_JA‐1 were determined to be $Il{6}_{JA-1}^D$ , $Ifn{g}_{JA-1}^D$ , and $Tlr{4}_{JA-1}^D$ , those of M_JA‐2 were $Eg{f}_{JA-2}^D$ and $Grb{2}_{JA-2}^D$ , of M_UA‐2 were $Tn{f}_{UA-2}^D$ and $Cd{4}_{UA-2}^D$ , of M_UA‐6 were $Akt{1}_{UA-6}^D$ , $Grb{2}_{UA-6}^D$ and $Ifnb{1}_{UA-6}^D$ , of M_UA‐7 were $Ccnd{1}_{UA-7}^D$ and $Il{2}_{UA-7}^D$ , of M_JU‐3 were $Il1b_{JU-3}^D$ , $Cd{4}_{JU-3}^D$ and $Stat{1}_{JU-3}^D$ , and those of M_JU‐4 were $Vegf{a}_{JU-4}^D$ and $Igf{1}_{JU-4}^D$ (Figure 5 a–g). All of the five PMDs were the unique drivers in synergistic drug combinations vs. control; except Cd4, the other four PMDs were the unique drivers in synergistic drug combinations vs. monotherapies.

Figure 5.

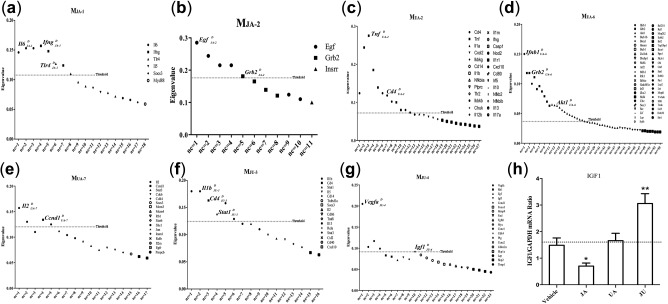
The pharmacological module driver (PMD) identification and validation. (a–g) The PMD determination in core modules by the method of “community core.” The “nc” is the number of communities, and the different shapes represent the top one node under each condition of the ncs. Nodes are considered as the PMD when the eigenvalue goes beyond the threshold (threshold = twice the median). (h) Validation of $Igf{1}_{JU-4}^D$ expression levels by real‐time polymerase chain reaction.*P < 0.05 vs. vehicle; **P < 0.01 vs. vehicle. The dotted line in h is the average expression level of the group. The ^D in the upper right corner of genes’ name means driver, and that in the lower right corner denotes its source. JA, jasminoidin; JU (jasminoidin and ursodeoxycholic acid); UA, ursodeoxycholic acid (UA).

In order to trace the source of component covariations, we imagined and reproduced this process by rewiring both core and noncore modules at a larger scale before and after the drug combinations (Figure 6 a,b). Subregions marked with different colors were almost traceable from multiple modules of the two monotherapy groups (Figure 6 a 2). The driver nodes of $Il1b_{JU-3}^D$ , $Cd{4}_{JU-3}^D$ , and $Stat{1}_{JU-3}^D$ must get rid of the shackles of the PMDs in the JA and UA modules (shown as purple lines) to become positive responders to the combination therapy, which could be regarded as the PMDs of the JU‐3 module. Along the arrow line, the dominant areas of PMDs were located. Only if the driver nodes in the monotherapy modules had linkages with the PMDs in the combination module, they could be detected in the combination group along with the modular evolution. The PMDs were divided into party driver and date driver. Party driver, such as $Il1b_{JU-3}^D$ and $Vegf{a}_{JU-4}^D$ , was defined as the node that had normal driving force to driver nodes; but for the date driver, such as State1, its driving behavior was manifested contingent. The driving relationship could also be observed after the two drivers in M_JU‐4 $Vegf{a}_{JU-4}^D$ and $Igf{1}_{JU-4}^D$ were investigated in detail (blue dotted line, Figure 6 b 1 , b3, b5).The core module structure based on overlapping PMDs before drug combination can be seen as the foundation of synergistic effect, and the core module structure based on nonoverlapping PMDs before drug combination can be seen as the complement of synergistic effect (Figure 6 c).

Figure 6.

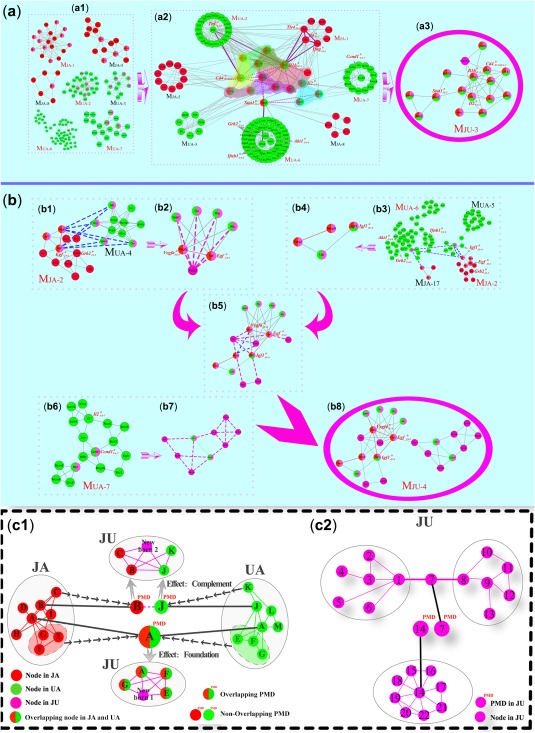
The paradigm of pharmacological module driver (PMD)‐induced M_JU3 and M_JU4 formation. (a) Formation process of M_JU‐3. (a1) Modules from the jasminoidin (JA) and ursodeoxycholic acid (UA) groups participate in the formation of M_JU‐3. (a2) Different modules from A1 around the PMD $Il1b_{JU-3}^D$, $Cd{4}_{JU-3}^D$, and $Stat{1}_{JU-3}^D$ in different regions contribute to the formation of the new module (for example, Il13, Cxcl10, Cd4, Traf6, Il5, Il2, and Rela from M_JA‐1 around $Il1b_{JU-3}^D$ collectively form the fan‐shaped region). The name of core modules is marked in red, the purple line link to the PMDs, the pink dashed arrows link to the new PMDs, and the colorful nodes are the overlapping nodes between different modules. (b) Formation process of M_JU‐4. The blue dotted lines in M_JU‐4 denote the nodes’ interaction between different modules, and the pink dotted lines link to the new nodes based on their interaction with other nodes in the module. The ^D in the upper right corner of genes’ name means driver, and that in the lower right corner denotes its source. (c1) The effect of PMDs before and after the drug combinations. Nodes in colors of red, green, and pink represent the JA, UA, and JU (jasminoidin and ursodeoxycholic acid) groups, respectively. (c2) The different kinds of newborn PMD in the JU group (drug combination).

Validation of PMDs by network topological variation

The degree, weighted degree, and PageRank of each PMD were higher than the average score except the degree and weighted degree of $Stat{1}_{JU-3}^D$ in M_JU‐3 (Supplementary Table S6). However, the betweenness centrality score of $Stat{1}_{JU-3}^D$ was 53, ranked third among all nodes, much higher than the average; and combined with the PageRank score, Stat1 was still an important node as PMD in M_JU‐3. Furthermore, a literature review was performed that showed that all the PMDs were related with cerebral ischemia in previous studies, and some of them were also considered as biomarkers of cerebral ischemia, such as $Il1b_{JU-3}^D$ , $Il{6}_{JA-1}^D$, and $Tn{f}_{UA-2}^D$ (Supplementary Table S7).

Biological verification of PMDs and relevant nodes in core modules

The $Igf{1}_{JU-4}^D$ and CYCLIN coexisted in p53 signaling pathway. The IGF1 reduced the infarct volume and improved neurological function after ischemia in rats following middle cerebral artery occlusion.25 Results of real‐time PCR showed that, compared with the vehicle group, IGF1 was significantly downregulated in the JA group (P < 0.05), but significantly upregulated in the JU group (P < 0.01; Figure 5 h). This indicated that, in the combination group, IGF1 might contribute to the recovery of neurological functions.

Treatment with a cyclin‐dependent kinase inhibitor can significantly reduce cell death in vitro.26 Our study showed that, compared with the sham group, the protein expression level of CYCLIN was significantly downregulated in the vehicle group (P < 0.05); and compared with the vehicle group, it was significantly downregulated in the JU group (P < 0.01; Supplementary Figure S5a). This indicated that the drug combination had the effect of neuroprotection following cerebral ischemia, but neither of the monotherapies showed such an effect.

The IL‐1RA is a target of brain ischemia, and localized striatal injection of IL‐1RA following cerebral ischemia in rats had the effect of cortical protection.27 It was a member of M_UA‐2, and our study showed that, compared with the sham group, the protein expression level of IL1RA was significantly downregulated in the vehicle group (P < 0.05); and compared with the vehicle group, it was significantly upregulated in the JA, UA, and JU groups (Supplementary Figure S5b). This indicated that JA, UA, and JU all had the effect of protection after cerebral ischemia. Moreover, another three pathways derived from this study: (1) extracellular matrix‐receptor interaction; (2) autoimmune thyroid disease; and (3) primary immunodeficiency, might be related to cerebral ischemia, pending further research and discussion in future work.

PMDs may drive pathway variation

The driver nodes are not only in the center of network topology, but also should regulate the components toward which they converge or through which crosstalk distinct signaling pathways exist.28 Many PMDs were found to be located upstream in known pathways; for example, $Igf{1}_{JU-4}^D$ and $Eg{f}_{JA-2}^D$ in a cancer‐related pathway (Supplementary Figure S6), $Il1b_{JU-3}^D$ in mitogen‐activated protein kinase signaling pathway, $Tlr{4}_{JA-1}^D$ in toll‐like receptor signaling pathway, $Grb{2}_{JA-2}^D$ and $Eg{f}_{JA-2}^D$ in glioma, and $Tn{f}_{UA-2}^D$ in apoptosis, $Il{2}_{UA-7}^D$ in Jak‐STAT signaling pathway. Because accessibility plays an important role in maintaining structural controllability, the upstream nodes play a more important role in control capability, which is rooted in the nature of control,29, 30 indicating that they may get involved in pathway variation. In addition, PMDs also acted as shared molecules to carry on pathway convergence of crosstalk31 between different pathways (Supplementary Figure S7), and thereby drive network convergence via pathway variation to exert different functions.

DISCUSSION

The game between the pathological module and pharmacological module for restoring cell homeostasis may mainly depend on the re‐allocation of information transmission in molecular networks. A similar process is described as rewiring the signaling network or nudging the pathophysiological networks to get rid of their abnormal state by drug action.32, 33, 34, 35, 36 Actually, the gray nodes, the neighbors of positively responsive members (Figure 3b ₁ –d₅), are those we really cannot neglect because of a consensus that many drugs do not target the actual disease‐associated proteins but their neighborhood.37

We used MDI to finalize the evaluation model of target module allosterism associated with external disturbances of nodes and modules. Just like affine transformation or conformational barcode hypothesis of cellular components,38, 39 modules may grow, contract, merge, split, be born, or die.2 Our data show that the JU group plays a more powerful role in overturning the pathological core module than the monotherapy groups. MDI may inspire novel understanding of how to eliminate the cascade of network failures based on topological structure and also provide quantitative evidence for synergistic attack of drug combinations.

Synergistic reconstruction of pharmacological modular infrastructure can be responsible for improving the core attacking power of drug combinations, which may benefit from the basic features of nonlinear discrete‐time system. Actually, coherent allostery of multimodules is an outcome caused by drug‐induced molecular hovering between memory and perturbance. We speculate that the production of a weak allosteric module may hinge on the fusion between precursors, but a strong allosteric module may be a result of rejecting. Because when adapting to disturbances, whether or not automatically, the system will make a choice to stay or to change.40 Coincidentally, this structural reconfiguration of system optimization was recently described approximatively as the complementation of plastic and rigid networks.39 However, not exactly the same, we want to emphasize on the whole emergence after drug combination that is rooted in the synergistic reconstruction of module components as well as the relocation of network signal navigation.

In an open system, we concentrate on who exactly is the internal responder of the dynamic changes. Network robustness can tolerate limited malfunctioning until self‐organized critical status starts appearing and being disturbed. This is an essential topic of practical reason, as it affects directly the efficiency of any process running on the networks severely.41 The critical phenomenon is the widespread appearance of phase transition in the nature.42 With the “sandpile model” and the “avalanche effect” as typical representation,43 exogenous‐endogenous collective dynamics may determine the next moment of an open system. As an important feature of system far‐from‐equilibrium (self‐organized criticality), self‐similarity has been proven to be the intrinsic property of complex network through the renormalization group theory.44 Interestingly, this property has also been extended to characterizing the community of the complex network.45 Developmental details of the scale‐free network underline a principle about preferential attachment of a few key nodes.46 Adaptive changes of network topology are also considered controlled by node behavior.47 Hence, we are highly concerned about the critical nodes called PMD owing to a similar process between module reconfiguration and scale‐free evolution of complex networks. It should be noted that unlike simple structural biology‐related module conformation, such as protein domain or dockerin,48, 49 in this case, conformation is originated from drug‐induced global molecular Van der Waals force covariation, including physical and nonphysical connections (heredity/mechanism correlation) between molecules.

It is well known that analysis of synergistic pharmacological mechanism still faces a serious challenge because of the temporary powerlessness in capturing molecular cluster dynamics. This prompted us to first present a paradigm called Quantitative Core Module and Driver Paradigm, by which a quantitative calculating method can reproduce the mutable details of synergistically attacking a disease before and after drug combination. In this study, we enriched the concepts of both core module and PMD, and demonstrated the ability of PMD in impelling the core module to experience allosteric transition. This dynamic point of strength coupled with the pharmacological modular flexibility will provide critical analysis strategy in the context of drug combination therapy. Although this study tends to be based on the structural analysis of the pure molecular network topology framework, in the future, we are not going to miss any opportunities of involving the structure and function fitting analysis between the core module and its driver.

Source of Funding

This work was supported by National Natural Science Foundation of China (81603486) and China Postdoctoral Science Foundation (2016M592735).

Conflict of Interest

The authors declared no conflict of interest.

Author Contributions

Y.Z. and Z.Z. wrote the manuscript. Z.W. designed the research. Y.Y., J.L., P.W., B.L., X.Z., and Y.C. performed the research. Y.Z. and Z.Z. analyzed the data.

Supporting information

Supporting Information Figures S1‐S7

Supporting Information Tables S1‐S7