Skip to main content
PMC home page
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences logoLink to Philosophical transactions. Series A, Mathematical, physical, and engineering sciences
. 2018 Apr 16;376(2120):20170291. doi: 10.1098/rsta.2017.0291

Microelectromechanical system gravimeters as a new tool for gravity imaging

Richard P Middlemiss 1,✉, Steven G Bramsiepe 1, Rebecca Douglas 1, Stefan Hild 1, James Hough 1, Douglas J Paul 2, Antonio Samarelli 1, Sheila Rowan 1, Giles D Hammond 1,✉
PMCID: PMC5915651  PMID: 29661979

Abstract

A microelectromechanical system (MEMS) gravimeter has been manufactured with a sensitivity of 40 ppb in an integration time of 1 s. This sensor has been used to measure the Earth tides: the elastic deformation of the globe due to tidal forces. No such measurement has been demonstrated before now with a MEMS gravimeter. Since this measurement, the gravimeter has been miniaturized and tested in the field. Measurements of the free-air and Bouguer effects have been demonstrated by monitoring the change in gravitational acceleration measured while going up and down a lift shaft of 20.7 m, and up and down a local hill of 275 m. These tests demonstrate that the device has the potential to be a useful field-portable instrument. The development of an even smaller device is underway, with a total package size similar to that of a smartphone.

This article is part of a discussion meeting issue ‘The promises of gravitational-wave astronomy’.

Keywords: geometric anti-spring, accelerometer, gravimeter, microelectromechanical system, sensor, transducer

1. Introduction

Gravimetry is defined as the measurement of g, the value of gravitational acceleration at a particular location. This value does not remain constant: it varies spatially with subterranean density; and it can also vary temporally if the density changes (via geophysical or human processes). If one can measure tiny changes in gravity, one can make deductions about the structure of the ground below.

(a). Applications of gravimetry

Gravimetry has been used in a wide number of fields. It has been exploited most extensively as an exploration tool in oil and gas exploration [1,2]; data can be collected about large-scale subterranean structures and deductions made about where resources might be found. There has also been a limited use of gravimetry in volcanology [3–7]; by monitoring temporal changes in gravity, it has been possible to assess whether magma is intruding below the volcano. Gravimetry has also be used in civil engineering to access the extent of sink holes [8]; in archaeology to find hidden crypts and voids [9]; and in the defence industry to search for tunnels [10,11].

(b). Commercial gravimeters

Commercially available gravimeters fall into two broad categories: absolute gravimeters and relative gravimeters. Absolute gravimeters measure the acceleration of an object in free fall; generally these are mechanical systems (e.g. the Micro-g LaCoste FG5 [12]), but recently atom clouds have been used instead of the falling mass; these are known as quantum gravimeters [13]. Absolute gravimeters are known for their precision and long-term stability, but they tend not to be portable. Relative gravimeters cannot make absolute measurements of gravity, but they can measure changes in gravity (both temporal and spatial). Relative gravimeters operate by measuring the change in displacement of a mass suspended from a spring (whether mechanical or magnetic). As the value of acceleration measured depends on the spring constant of the spring—which can vary with changing temperature—relative gravimeters are more prone to drift (with the exception of superconducting gravimeters, which have been demonstrated to maintain a stability similar to that of an absolute gravimeter [14]). Relative gravimeters can be made smaller than absolute gravimeters; therefore, most gravity measurements made in the field are acquired using such an instrument. There are a limited number of field-portable gravimeters on the market. The Scintrex CG6 is often thought of as the leading device, but several other devices are used: LaCoste & Rhomberg gravimeters are still used widely, their successor made by ZLS and a new iteration of the Burris gravity metre [15].

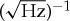Commercial gravimeters mostly achieve a noise floor of the order of a few μGal Inline graphic, where 1 μGal is equivalent to 10−8 m s−2, and where Inline graphic signifies an integration time of 1 s. This is a level of sensitivity that makes them useful for the wide range of applications listed above. Gravimeters are, however, very expensive, with an absolute device costing around £300 K, and a new relative gravimeter costing around £60 K. As already mentioned, absolute gravimeters are not generally field-deployable, but even field-portable relative devices are not available under 5 kg. There is the potential to make devices significantly smaller and cheaper than those currently available via the use of microelectromechanical systems (MEMS) accelerometers.

(c). Microelectromechanical systems accelerometers

MEMS accelerometers are tiny mechanical structures, micro-machined from silicon. Vaganov developed the first MEMS-based accelerometer in 1975 [16], shortly followed by Roylance & Angell in 1979 [17]. The latter device had a sensitivity of 1 Gal. MEMS accelerometers became much more ubiquitous, however, with the introduction of car airbags in the 1990s. Air bags needed cheap accelerometers that could detect the sharp deceleration indicative of a car crash—MEMS were the perfect solution to this market need. MEMS accelerometers are now used in every smartphone to monitor the orientation of the device, and adjust the screen accordingly. Many apps also use the accelerometer functionality for augmented reality applications [18].

These mobile phone MEMS accelerometers are extremely cheap to manufacture (and are obviously light weight), but as common as they are, they cannot compete with commercial gravimeters in terms of either sensitivity or stability. The iPhone 5, for example, uses an accelerometer with a sensitivity of 234 mGal [19].

A small number MEMS accelerometers have now been developed that achieve extremely good sensitivity. Devices by Krishnamoorthy et al. [20], Quietseis [21] and Pike et al. [22] have noise floors of 17, 15 and 0.3 μ Gal, respectively. These devices were all designed as seismometers, so although they have similar acceleration sensitivities to commercial gravimeters, they do not operate with a stability that would allow them to monitor slowly varying gravitational signals. ‘Stability’ is used broadly here. All electronic devices are prone to low-frequency noise. There are many various causes for low-frequency noise, and it is difficult to reduce their effects. These sources of noise, however, have to be tackled in order to maintain a low acceleration noise floor at low frequencies (i.e. over long periods). In 2009, Sandia National Laboratories conjectured that MEMS accelerometers may expand into ‘long period’ stability within the next 10 years. ‘Long period’ was defined as 0.01 Hz [23]. It has been expressed, however, that such accelerometers would be desirable [23–25].

2. Wee-g gravimeter

With the aim of making a small, cheap, stable and sensitive relative MEMS gravimeter, a device was designed by the authors, and named the Wee-g [26–28]. The device comprises a mass on a spring, and an optical sensor that monitors the displacement of the mass. By monitoring the displacement, the local acceleration can be measured using equation (2.1), which is derived by equation from Newton’s Second Law of Motion and Hooke’s Law:

2. 2.1

where x is the displacement of the mass, m and k is the spring constant.

(a). Geometric anti-springs

From equation (2.1) it is clear that to increase the gravitational sensitivity, one must either improve the sensitivity of the displacement sensor, or optimize the ratio of k/m. Ideally, a system would be made with a heavy mass and a soft spring. To achieve such a requirement with a Hooke’s Law spring can be challenging: the spring must be made longer and/or thinner to make it softer. This, in turn, can mean that the spring will flex in many different directions. This is not desirable because it is hard to decouple motion in multiple axes using a single displacement sensor. An ideal system would therefore be constrained to move in only one axis.

Taking inspiration from the VIRGO gravitational wave detector mirror suspensions [29–32], a geometric anti-spring was considered. This is a nonlinear spring design that gets softer with increasing extension [33]. Figure 1 shows the design for the MEMS mass-on-spring system. A central mass is suspended from arched springs, much like those used in the VIRGO detector as seismic isolation systems. The springs are designed to have a ribbon structure, limiting the out-of plane motion. It is important to consider the nonlinearity of the geometric anti-spring because a such nonlinear response will mean that the spring constant, k, will be different at either side of the null position. This phenomenon is known as ‘astatization’ [34]. Ultimately, the system will be run in force feedback mode so as to hold the mass in its null position, with the input force of the feedback loop being used as a metric of the acceleration change (instead of displacement). In the short term, however, it was noted that as the gravitational loading increases on the anti-spring system, the resonant frequency goes through a minimum [26]. Operating at this minimum means that the spring regains a Hooke’s Law behaviour—to first order—militating against the effect of astatization.

Figure 1.

Figure 1.

Open in a new tab

The right-hand image is the design of the MEMS relative gravimeter. The central mass is suspended from geomtric anti-springs. These nonlinear springs get softer with displacement. An SEM image of the springs can be observed in the left-hand image. The springs are manufactured with a ribbon-like structure, constraining the motion to a single axis as much as possible. (Online version in colour.)

(b). Fabrication

The MEMS devices are fabricated from 〈100〉 silicon using a photolithography process. A photoresist (a liquid polymer used in the nano-fabrication industry) is spun onto the surface and a photolithography mask is placed over the top. This mask is made of chromed glass with clear sections representing the desired pattern. When exposed to ultraviolet light, the resist under the clear sections of the mask breaks down and can be developed in a solution, leaving the MEMS pattern in resist on the silicon. This resist is then used as a mask to etch the silicon itself. The silicon is coated on its underside with a thin layer of silicon dioxide. After the resist mask has been patterned, the samples are stuck down to a carrier wafer and placed inside a silicon etch tool.

The etching was conducted using the Bosch process [35]. This process is used to etch silicon in a highly anisotropic fashion (i.e. where vertical etching is required that cannot be achieved with a wet chemical etch). The exposed silicon is cyclically etched isotropically using sulphur hexaflouride (SF6), passivated using octaflourocyclobutane (C4F8) and bombarded with a beam of ions to break down the C4F8 on the horizontal surfaces.

(c). Optical readout

The optical sensor used to monitor the displacement of the MEMS device is a ‘shadow sensor’, similar to those used in the Advanced LIGO gravitational wave detectors [36]. The shadow sensor, with the MEMS attached, is presented in figure 2. The components are mounted on a fused silica ‘c’-shaped structure. An LED is shone at a split-photodiode, and the MEMS mounted in between the two. As the mass moves, it modulates the shadow on the photodiode. This modulation causes a change in the photocurrent output, which can be used as a metric for the motion after a calibration. A split photodiode configuration was used because this allowed the output to be wired differentially [37,38], a standard method of configuring light-balancing circuits. The two wires from each side of the split photodiode were wired in reverse parallel and operated in photovoltaic mode. If both sides were evenly illuminated, then zero signal would be seen on the output. This meant that the output signal could be amplified to a greater extent (therefore, increasing the signal-to-noise ratio (SNR)).

Figure 2.

Figure 2.

Open in a new tab

An optical shadow sensor is used to monitor the displacement of the MEMS device. An LED is shone at a split-photodiode. Any movement in the shadow cast by the mass modulates the photocurrent output of the photodiode, which can be used as a proxy for displacement. (Online version in colour.)

When running the system, the LED was modulated at a frequency of 107 Hz. The output photocurrent of the differentially configured photodiodes was passed through a current-to-voltage (transimpedence) amplifier. This converted the photocurrent into a voltage, and amplified the signal by a factor of 1 million (1 μA V−1). The signal was then passed through an analogue lock-in amplifier. This used the reference from the signal generator to de-modulate the signal, converting the signal from AC to DC.

(d). Thermal control

As the spring constant can change with temperature (via the Young’s modulus), it is important to maintain the temperature of the MEMS to a level of around 1 mK. This was achieved via closed-loop temperature control of the MEMS chip itself, the fused silica ‘c’ of the shadow sensor, and a copper thermal shield that enclosed the shadow sensor. Resistive heaters and thermometers were glued to each of these components. The temperatures were monitored using the thermometers and proportional–integral–derivative (PID) control loops were used to control the voltage supplied to the heaters. The components were held at set points up to 5° above ambient temperature. The dominant mechanism by which the mechanical behaviour of the MEMS device is effected by temperature is via the change in Young’s modulus of the springs. A change in the Young’s modulus has the effect of altering the spring constant, k, of the springs. A change of 1 mK thus results in an acceleration error of 25 μGal [26].

The entire sensor (and heat shield) were enclosed within a vacuum tank and evacuated. The vacuum reduced the effect of conductive heat transfer, therefore, reducing the load on the closed loop temperature control.

(e). Lab-based results

To assess the efficacy of the gravimeter, the Earth tides were measured. The Earth tides are caused by tidal forces in the Earth/Moon/Sun system [39]. These forces (as well as the rotational dynamics of the Earth) cause the globe to alter its shape. The way in which the shape changes is affected by the mechanical properties of the rock [40]. The magnitude of the signal is further complicated by the presence of liquid (oceans/large lakes, etc.) near the measurement locations. The ocean tides are not necessarily in phase with the Earth tide signal and can cause an error in the estimated value for a given location/time. In simple terms, however, the Earth tides cause the distance from the centre of the Earth to the surface to modulate. This modulation can be as much as ±50 cm. In Glasgow this range is closer to 20 cm. A change in the local value of acceleration, g, will therefore also be observed. For Glasgow it will change by up to around 200 μGal. Measuring this signal would demonstrate both the sensitivity of the MEMS device and its stability. The results of such a measurement are presented in figure 3. The red series is the expected signal for the measurement location (Glasgow, UK), and the blue series shows the acceleration measurement made by the gravity sensor. These data were originally published by Middlemiss et al. [26]. The data have been regressed against temperature to remove correlated variations between the output signal and the various temperature measurements [27]. A linear drift of 150 μGal has also been removed from the data, thought to be caused by ageing of the LED in the optical sensor. An Allan deviation analysis of the data are performed in Middlemiss et al. [26] to assess the drift characteristics of the sensor.

Figure 3.

Figure 3.

Open in a new tab

The black series is the theoretical Earth tide signal expected at the measurement location in Glasgow for the defined dates. The grey series is the full-noise data from the MEMS gravimeter. These data were first presented in Nature by Middlemiss et al. [26].

(f). Wee-g miniaturization

Since the measurement of the Earth tides, the gravimeter has been miniaturized. In the original system, the electronics required to run the device occupied an entire rack (figure 4). A bespoke printed electronics board was designed to replace this. The electronics board was controlled using a dsPIC micro-controller. This was used to operate the PID temperature control, modulate the LED and demodulate the photodiode output using a novel software-based lock-in amplifier [41]. The data could be recorded on a computer via a USB connection, or onto an SD card on the board itself. The system was powered using a lithium-ion battery pack. The 1 m tall vacuum tank was replaced with a 10×10 cm vacuum enclosure. This enclosure could maintain its vacuum with a powerless getter pump. Both the vacuum tank, the electronics board and the battery pack were mounted on an aluminium plate, which could be levelled using three micrometre legs.

Figure 4.

Figure 4.

Open in a new tab

A field-portable version of the MEMS gravimeter has been constructed. The rack-mounted electronic components have been replaced with an electronics board, and the large vacuum tank has been replaced by an enclosure with dimensions 10×10 cm. The new gravimeter has the same functionality as the laboratory-based system. (Online version in colour.)

(g). Field tests

Gravitational acceleration varies with altitude according to the following expression [42]:

(g). 2.2

where G is the gravitational constant, ME is the mass of the Earth and RE is the radius of the Earth. This variation is known as the ‘free-air effect’. This expression contains the assumption that there is no material between the geoid and the measurement location. Measurements where this is not the case have some added complexity. If a measurement is taken on top of a mountain, one must also take into account the attractive force of the additional mass between the geoid and the measurement location. This additional factor is known as the ‘Bouguer Correction’, and it acts to increase the value of g. The Bouguer Correction is given by

(g). 2.3

where H is the thickness of the material between the geoid and the measurement location (assumed to be an infinitely wide slab of material) and ρ is the density of this material.

When predicting an expected change in gravitational acceleration with altitude, one must factor in both the free-air and Bouguer effects. Added complexity comes from the topography around the station that may vary from the overly simplistic infinite-slab model, and from uncertainty in subterranean densities.

To test whether the field-portable gravimeter was working effectively, the gravimeter was placed in a lift to see whether a change in gravitational acceleration could be observed. The resulting data are presented in figure 5. The first measurement was made at the top of the lift shaft. The gravimeter was levelled and data recorded for a period of around 300 s. The lift was then taken to the top of the building, the gravimeter relevelled and allowed to settle (the transition and settling time are not presented in the graph). A second measurement was then taken, again for around 300 s. This process was then repeated at the bottom and the top of the building in a cyclical fashion. A clear difference in gravitational acceleration can be observed between the two measurement locations. The magnitude of this difference—4.51 mGal—aligns with the estimation of the expected gravitational signal expected at this location, given the free-air and Bouguer effects. The black error bars represent the standard deviation of the data at each measurement location. These bars indicate that the measurement was made with an SNR of 14.25.

Figure 5.

Figure 5.

Open in a new tab

The difference in gravitational acceleration observed between the bottom and top of a 20.7 m lift shaft. These data were originally presented in Middlemiss et al. [43]. A total acceleration change of 4.51× 10−5 m s−2 (4.51 mGal) was observed.

To further test the gravimeter in more harsh environmental conditions, a similar test was carried out on a local hill with a hight of 275 m. Measurements were taken at the bottom, top and bottom again of the hill in the same manner as those presented in figure 5. The results of these tests can be observed in figure 6. An acceleration range of 46.2 mGal was measured with an SNR of 15.88. The data were noisier than that recorded inside due to the effect of wind buffeting and larger temperature gradients. As discussed in Middlemiss et al. [43], this acceleration range lay within the range predicted for the site, taking into account the free-air and Bouguer effects, terrain effects and the possible range in rock density.

Figure 6.

Figure 6.

Open in a new tab

The data from a test of the MEMS gravimeter in an outside field test. From left to right, the three data points represent data recorded at the bottom, top and bottom of the hill (over a total altitude range of 275 m). An acceleration range of 4.62×10−4 m s−2 (46.2 mGal) was measured. This plot was originally presented in Middlemiss et al. [43].

3. Future plans

The results presented in figures 5 and 6 demonstrate that progress is being made towards the development of a practical field gravimeter. Without further miniaturization, however, the device will not achieve the required compact size and potential low cost. Work is now being conducted to significantly reduce the size of the instrument. The MEMS device is being packaged in a commercial MEMS enclosure with dimensions of 40×20×2 mm, and weighing under 40 g. It is expected that with these advances that the entire system could approach the size of a smartphone in the near future. Such an instrument could allow new gravity imaging modalities: multi-pixel gravity-imaging arrays could become possible for the first time; and devices of this weight would be small enough to be flown on a drone platform.

Acknowledgements

The authors thank the staff and other users of the James Watt Nanofabrication Centre for help and support in undertaking the MEMS fabrication.

Data accessibility

The research data relevant to this article are stored on the University of Glasgow’s Enlighten Repository (http://dx.doi.org/10.5525/gla.researchdata.213).

Authors' contributions

R.P.M. was responsible for the fabrication of the MEMS chips (with supervision from D.J.P. and G.D.H.), and led the writing of the manuscript. R.P.M., S.G.B., R.D., A.S. and G.D.H. assembled the gravimeter iterations and conducted the experiments/field tests. R.P.M. and G.D.H. performed the analysis of the experimental data. S.G.B. and G.D.H. developed the electronic readout for the gravimeter. D.J.P. and G.D.H. developed the initial conceptual design of the gravimeter. S.H. provided guidance on the optical sensing methodologies. J.H. and S.R. helped to develop the methodology of using geometric anti-springs for the use in MEMS gravimeters and provided critical review of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by the Royal Society Paul Instrument Fund, STFC grant no. ST/M000427/1 and the UK National Quantum Technology Hub in Quantum Enhanced Imaging (EP/M01326X/1).

References

  • 1.Barnes G, Barraud J. 2012. Imaging geologic surfaces by inverting gravity gradient data with depth horizons. Geophysics 77, G1–G11. ( 10.1190/geo2011-0149.1) [DOI] [Google Scholar]
  • 2.Rim H, Li Y. 2015. Advantages of borehole vector gravity in density imaging. Geophysics 80, G1–G13. ( 10.1190/2015-0420-TIOGEO.1) [DOI] [Google Scholar]
  • 3.Fernández J, Pepe A, Poland MP, Sigmundsson F. 2017. Volcano Geodesy: Recent developments and future challenges. J. Volcanol. Geotherm. Res. 344, 1–12. ( 10.1016/j.jvolgeores.2017.08.006) [DOI] [Google Scholar]
  • 4.Carbone D, Poland MP, Diament M, Greco F. 2017. The added value of time-variable microgravimetry to the understanding of how volcanoes work. Earth-Sci. Rev. 169, 146–179. ( 10.1016/j.earscirev.2017.04.014) [DOI] [Google Scholar]
  • 5.Aparicio SS-M, Sampedro JA, Montesinos FG, Molist J. 2014. Volcanic signatures in time gravity variations during the volcanic unrest on El Hierro (Canary Islands). J. Geophys. Res. Solid Earth 119, 5033–5051. ( 10.1002/2013JB010795) [DOI] [Google Scholar]
  • 6.Battaglia M, Gottsmann J, Carbone D, Fernandez J. 2008. 4D volcano gravimetry. Geophysics 73, WA3–WA18. ( 10.1190/1.2977792) [DOI] [Google Scholar]
  • 7.Rymer H, Williams-jones G, Keynes M. 2000. Gravity and deformation measurements. Geophys. Res. Lett. 27, 2389–2392. ( 10.1029/1999gl011293) [DOI] [Google Scholar]
  • 8.Kaufmann G. 2014. Geophysical mapping of solution and collapse sinkholes. J. Appl. Geophy. 111, 271–288. ( 10.1016/j.jappgeo.2014.10.011) [DOI] [Google Scholar]
  • 9.Panisova J, Pasteka R. 2009. The use of microgravity technique in archaeology: a case study from the St. Nicolas Church in Pukanec, Slovakia. Contributions to Geophysics and Geodesy 39, 237–254. ( 10.2478/v10126-009-0009-1) [DOI] [Google Scholar]
  • 10.Butler DK. 1984. Microgravimetric and gravity gradient techniques for detection of subsurface cavities. Geophysics 49, 1084–1096. ( 10.1190/1.1441723) [DOI] [Google Scholar]
  • 11.Romaides AJ, Battis JC, Sands RW, Zorn A, Benson DO, DiFrancesco DJ. 2001. A comparison of gravimetric techniques for measuring subsurface void signals. J. Phys. D Appl. Phys. 34, 433–443. ( 10.1088/0022-3727/34/3/331) [DOI] [Google Scholar]
  • 12.Van Camp M. 2005. Uncertainty of absolute gravity measurements. J. Geophys. Res. Solid Earth 110, B05406 ( 10.1029/2004JB003497) [DOI] [Google Scholar]
  • 13.Hardman KS. et al. 2016. Simultaneous precision gravimetry and magnetic gradiometry with a Bose-Einstein condensate: a high precision, quantum sensor. Phys. Rev. Lett. 117, 1–5. ( 10.1103/PhysRevLett.117.138501) [DOI] [PubMed] [Google Scholar]
  • 14.Riccardi U, Rosat S, Hinderer J. 2011. Comparison of the Micro-g LaCoste gPhone-054 spring gravimeter and the GWR-C026 superconducting gravimeter in Strasbourg (France) using a 300-day time series. Metrologia 48, 28–39. ( 10.1088/0026-1394/48/1/003) [DOI] [Google Scholar]
  • 15.Jentzsch G. 2008. The automated Burris gravity meter—a new instrument using an old principle. In Proc. Symp. Terrestrial Gravimetry: Static and Mobile Measurements, St. Petersburg, Russia, 20–23 August 2007, pp. 21–28. Munich, Germany: International Association of Geodesy.
  • 16.Middelhoek S. 2000. Celebration of the tenth transducers conference: the past, present and future of transducer research and development. Sens. Actuators A 82, 2–23. ( 10.1016/S0924-4247(99)00395-7) [DOI] [Google Scholar]
  • 17.Roylance LM, Angell JB. 1979. A batch-fabricated silicon accelerometer. IEEE. Trans. Electron. Devices 26, 1911–1917. ( 10.1109/T-ED.1979.19795) [DOI] [Google Scholar]
  • 18.Chen W-Y, Wang M, Wu Z-S. 2017. Augmented reality game control of handy devices using a triaxial accelerometer and an electronic compass. Sen. Mater. 29, 727–739. ( 10.18494/SAM.2017.1488) [DOI] [Google Scholar]
  • 19.D’Alessandro A, D’Anna G. 2013. Suitability of low-cost three-axis MEMS accelerometers in strong-motion seismology: tests on the LIS331DLH (iPhone) accelerometer. Bull. Seismol. Soc. Am. 103, 2906–2913. ( 10.1785/0120120287) [DOI] [Google Scholar]
  • 20.Krishnamoorthy U, Olsson RH, Bogart GR, Baker MS, Carr DW, Swiler TP, Clews PJ. 2008. In-plane MEMS-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuators A 145-146, 283–290. ( 10.1016/j.sna.2008.03.017) [DOI] [Google Scholar]
  • 21.Lainé J, Mougenot D. 2014. A high-sensitivity MEMS-based accelerometer. Lead. Edge 33, 1234–1242. ( 10.1190/tle33111234.1) [DOI] [Google Scholar]
  • 22.Pike WT. et al. 2016. A silicon seismic package (SSP) for planetary geophysics. In 47th Lunar and Planetary Sci. Conf., The Woodlands, TX, 21–25 March, p. 2081. Houston, TX: Lunar and Planetary Institute.
  • 23.Merchant BJ. 2009. MEMS applications in seismology. In Seismic Instrumentation Technology Symposium, Palm Springs, CA. (http://www.iris.edu/hq/instrumentation_meeting/files/pdfs/MEMS_Seismology.pdf).
  • 24.Stauffer J-M. 2004. Market opportunities for advanced MEMS accelerometers and overview of actual capabilities vs. required specifications. In IEE Xplore: Position Location and Navigation Symposium, Monteray, CA, 26–29 April, pp. 78–82. Piscataway, NJ: IEEE.
  • 25.Hons MS, Stewart RR. 2008. Could MEMS-based accelerometers be used for gravity surveys. CREWES Res. Rep. 20, 1–7. [Google Scholar]
  • 26.Middlemiss RP, Samarelli A, Paul DJ, Hough J, Rowan S, Hammond GD. 2016. Measurement of the Earth Tides with a MEMS Gravimeter. Nature 531, 614–617. ( 10.1038/nature17397) [DOI] [PubMed] [Google Scholar]
  • 27.Middlemiss RP. 2016. A practical MEMS gravimeter. PhD thesis, University of Glasgow, UK.
  • 28.Campsie P, Hammond GD, Middlemiss RP, Paul DJ, Samarelli A. 2015. Patent: Measurement of Acceleration.
  • 29.Bertolini A, Cella G, Desalvo R, Sannibale V. 1999. Seismic noise filters, vertical resonance frequency reduction with geometric anti-springs: a feasibility study. Nucl. Instr. Meth. Phys. Res. A 435, 475–483. ( 10.1016/S0168-9002(99)00554-9) [DOI] [Google Scholar]
  • 30.Cella G, Sannibale V, Desalvo R, Márka S, Takamori A. 2005. Monolithic geometric anti-spring blades. Nucl. Instr. Meth. Phys. Res. A 540, 502–519. ( 10.1016/j.nima.2004.10.042) [DOI] [Google Scholar]
  • 31.Acernese F, De Rosa R, Giordano G, Romano R, Barone F. 2015. Low frequency inertial control strategy for seismic attenuation with multi-stage mechanical suspensions. Proc. SPIE 9431, 1–11. ( 10.1117/12.2008629) [DOI] [Google Scholar]
  • 32.Abbott BP. et al. 2016. Direct observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 1–16. ( 10.1103/PhysRevLett.116.061102) [DOI] [PubMed] [Google Scholar]
  • 33.Ibrahim RA. 2008. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 314, 371–452. ( 10.1016/j.jsv.2008.01.014) [DOI] [Google Scholar]
  • 34.Melchior P. 2008. Gravimetric measuring techniques. In Physical methods, instruments and measurements (ed. YM Tsipenyuk), pp. 259–290, vol. II. Oxford, UK: Eolss Publishers.
  • 35.Laermer F, Schilp A. 1996. Method of anisotropic etching of silicon. US patent number: 5,501,893.
  • 36.Carbone L. et al. 2012. Sensors and actuators for the advanced LIGO mirror suspensions. Class. Quantum Grav. 29, 115005 ( 10.1088/0264-9381/29/11/115005) [DOI] [Google Scholar]
  • 37.Lockerbie NA, Tokmakov KV. 2014. A ‘Violin-Mode’ shadow sensor for interferometric gravitational wave detectors. Meas. Sci. Technol. 25, 125110 ( 10.1088/0957-0233/25/12/125110) [DOI] [Google Scholar]
  • 38.Hamamatsu Photonics. 2014. Opto-semiconductor handbook, 1st edn Hamamatsu, Japan: Hamamatsu Photonics. [Google Scholar]
  • 39.Farrell WE. 1973. Earth tides, ocean tides and tidal loading. Phil. Trans. R. Soc. A 274, 253–259. ( 10.1098/rsta.1973.0050) [DOI] [Google Scholar]
  • 40.Agnew DC. 2005. Earth tides: an introduction. Technical Report.
  • 41.Bramsiepe SG, Middlemiss RP, Douglas R, Paul DJ, Loomes D, Hammond GD. In press. A high stability optical shadow sensor with applications for precision accelerometers. IEEE Sens. J. (http://arxiv.org/abs/1711.01253).
  • 42.Torge W. 1989. Gravimetry. Berlin, Germany: De Gruyter. [Google Scholar]
  • 43.Middlemiss R, Bramsiepe S, Douglas R, Hough J, Paul D, Rowan S, Hammond G. 2017. Field tests of a portable MEMS gravimeter. Sensors 17, 2571 ( 10.3390/s17112571) [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The research data relevant to this article are stored on the University of Glasgow’s Enlighten Repository (http://dx.doi.org/10.5525/gla.researchdata.213).

Articles from Philosophical transactions. Series A, Mathematical, physical, and engineering sciences are provided here courtesy of The Royal Society

RESOURCES