Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jan 12;140(4):1415–1422. doi: 10.1021/jacs.7b11061

Water-Assisted Hole Trapping at the Highly Curved Surface of Nano-TiO2 Photocatalyst

Kenji Shirai †, Gianluca Fazio ‡, Toshiki Sugimoto †,⊥,*, Daniele Selli ‡, Lorenzo Ferraro ‡, Kazuya Watanabe †, Mitsutaka Haruta §, Bunsho Ohtani ∥, Hiroki Kurata §, Cristiana Di Valentin ‡,*, Yoshiyasu Matsumoto †,*
PMCID: PMC5916465  PMID: 29325412

Abstract

graphic file with name ja-2017-11061r_0006.jpg

Heterogeneous photocatalysis is vital in solving energy and environmental issues that this society is confronted with. Although photocatalysts are often operated in the presence of water, it has not been yet clarified how the interaction with water itself affects charge dynamics in photocatalysts. Using water-coverage-controlled steady and transient infrared absorption spectroscopy and large-model (∼800 atoms) ab initio calculations, we clarify that water enhances hole trapping at the surface of TiO2 nanospheres but not of well-faceted nanoparticles. This water-assisted effect unique to the nanospheres originates from water adsorption as a ligand at a low-coordinated Ti–OH site or through robust hydrogen bonding directly to the terminal OH at the highly curved nanosphere surface. Thus, the interaction with water at the surface of nanospheres can promote photocatalytic reactions of both oxidation and reduction by elongating photogenerated carrier lifetimes. This morphology-dependent water-assisted effect provides a novel and rational basis for designing and engineering nanophotocatalyst morphology to improve photocatalytic performances.

Introduction

Heterogeneous photocatalysis is versatile: it decomposes pollutants in air and water, kills microbes, and even has great potential for producing hydrogen out of water with sustainable sunlight. The photocatalytic reactions in these applications are driven by electrons and holes generated by photoexcitation across the band gap of semiconductor particles. Extensive studies on heterogeneous photocatalysis in the past have revealed that one of the biggest obstacles to improving photon energy conversion efficiency is an effective loss channel of photogenerated carriers by rapid electron–hole recombination. However, there is still a fundamental open question: it is not yet clear how water is involved in the photocarrier dynamics at the surface of photocatalysts, although they are usually operated in an aqueous or wet environment. The rate-determining process in photocatalysis is the oxidation of molecules at the photocatalysts surface, where long-living trapped photogenerated holes play a crucial role. Moreover, hole trapping enables electrons to live longer, which also promotes reduction reactions such as hydrogen evolution in water splitting. Therefore, the understanding at a molecular level of the role played by water in the key process of hole trapping is of paramount importance for an effective design of high performance photocatalysts.

TiO2 has been a prototype material to study the mechanism of heterogeneous photocatalysis.1−5 Trapped carriers in TiO2 nanoparticles have been intensively investigated with several experimental techniques. Electron paramagnetic resonance (EPR) studies6−9 have clarified that photogenerated electrons are trapped as Ti3+ species, while holes are trapped at the surface of nanoparticles as O– species. However, the application of EPR spectroscopy is mostly limited to low temperature. Transient absorption spectroscopy has been applied in a wide time scale and wavelength range.10−21 In particular, it is well-known that photogenerated electrons in the conduction band and in shallow trap states reveal a Drude-like broad absorption band in the mid infrared.16,21 Trapped carriers have been also investigated theoretically, although most of the calculations were done using slab-type models of anatase TiO2, mimicking a single-crystal surface.22,23 In-gap states originating from extra electrons or holes have been confirmed when proper self-interaction corrected methods (hybrid functionals) are used for density functional theory (DFT) calculations.24,25 The calculations suggest that two-coordinated bridging oxygen, O2c, is the primary candidate for surface hole trapping. EPR7 and time-resolved FTIR in the second to minute time scale21 showed that water adsorbates stabilize surface trapped holes and retard the charge recombination rate. However, the role of interfacing water in charge trapping dynamics is still unclear.26,27

Despite intensive research in the past, we confront serious problems for exploring the carrier trapping mechanism in heterogeneous photocatalysis. The problems are related to two serious gaps between fundamental and application oriented studies: the material and pressure gaps. On the one hand, a tremendous material gap originates from the fact that nanoparticles used in realistic photocatalytic reactions have various sizes, shapes, and morphologies. In particular, highly curved surfaces were reported to more strongly bind chemical species and, in general, to present an enhanced reactivity.28,29 For these reasons, besides better known nanospheres or nanorods, novel roundish nanobjects are currently attracting a lot of attention.30−32 Numerous calculations on slabs of a single crystal provide little information on the hole trapping mechanism at the surface of realistic nanoparticles. On the other hand, most of the experimental studies have been performed either in an ultrahigh vacuum or in an aqueous environment. There is a sizable pressure gap between the two experimental conditions.

To fill the two gaps, both experimentally and theoretically, we have tackled this complex problem through a two-dimensional systematic approach: on one side, we have investigated TiO2 nanoparticles with distinctly different morphologies (roundish nanocrystallites and well-faceted nanocrystallites of decahedral and octahedral anatase particles), and, on the other, we have gradually increased the water coverage in a controlled manner. Hybrid DFT calculations were run on very large model systems of ∼800 atoms to be as close as possible to experimental conditions. Here, we demonstrate that a surface OH group at the curved surface of nanosphere effectively traps a hole in contrast to an OH group at the flat surface of faceted nanocrystallite, and this trapping ability is further enhanced by adsorption of an additional water molecule.

Materials and Methods

Samples

Experiments were performed with three kinds of anatase TiO2 nanoparticles. As the faceted particles, we used decahedral anatase particle (DAP) and octahedral anatase particle (OAP) prepared by gas-phase reaction and hydrothermal reaction, respectively.33,34 As the roundish anatase particles without well-developed flat facets, we used commercially available ST-01 of Ishihara Sangyo that has been used as a standard sample in comparison regarding photocatalytic activity and in studies of the mechanism of photocatalysis of anatase TiO2 nanoparticles.35−37 The structure and morphology of nanoparticles were observed with transmission electron microscopy (JEM-ARM200F/JEOL) and X-ray diffraction (miniflex600/Rigaku). The surface area and the absolute amount of water adsorption were determined with volumetric analysis (BELSORP-miniII/BeL JAPAN). Impurities of all of the samples were below the detection limit of X-ray photoelectron spectroscopy (<1%).

TAS and DRIFTS Measurements

The light source for transient absorption (TA) spectroscopy was a fs-Ti:sapphire laser with a regenerative amplifier (Spitfire, Spectra Physics, 800 nm, 170 fs)38 that generated pump pulses at 400 nm and probe pulses at 4000 nm. DRIFT spectra of the TiO2 nanoparticles were measured by an FTIR spectrometer (FT-IR7000M/Varian) equipped with a mercury cadmium telluride (MCT) detector. The background for the IR measurements was taken with Si powder in a diffuse reflectance mode. The intensity of IR absorption was estimated by the Kubelka–Munk equation.

Computational Methods

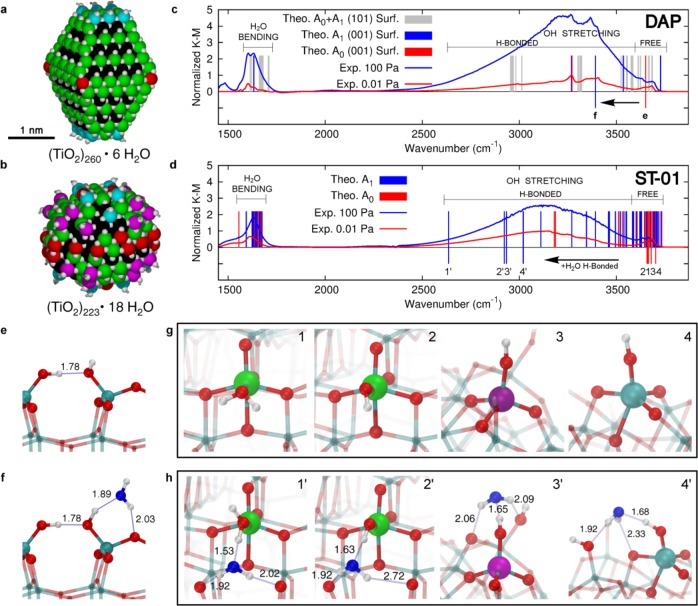
All density functional theory (DFT) calculations were performed with the CRYSTAL1439 code, where the Kohn–Sham orbitals are expanded in Gaussian localized basis functions, employing the B3LYP40,41 hybrid functional. The models for the faceted (NC) and spherical (NS) nanoparticles (Figure 3) were carved from bulk anatase and saturated with H atoms to obtain chemically stable systems with stoichiometries of (TiO2)260·6H2O and (TiO2)223·18H2O, respectively.42 To determine a stable minimum energy structure for NS, a global optimization procedure (simulated annealing) by means of the computational efficient density functional tight-binding method (DFTB)43−45 was carried out before a final optimization run with DFT-B3LYP. It is common practice to describe flat anatase facets with slab models. In this work, the recourse to a 1 × 3 and a 4 × 2 slab supercell, with a thickness of three and four atomic trilayers, for the (101) and (001) facets, respectively, was limited to the calculation of (i) the vibrational frequencies of water adsorbates and (ii) the hole states for the (001). For all other calculations, the faceted nanoparticle model (NC) was employed. A Monkhorst–Pack k-point grid was used to sample the Brillouin zone: 2 × 2 × 1 for the (101) surface and 1 × 2 × 1 for the (001) surface. Harmonic frequencies have been calculated by numerical differentiation of the gradient vector, using a “two-point” formula, and rescaled according to the experimental symmetric stretching mode of gas water.46 Further computational details are given in Supporting Information section 2.

Figure 3.

Figure 3

Open in a new tab

Vibrational structures of water and hydroxyl adsorbates on anatase TiO2 nanoparticle models. (a) Space-filling representation of the faceted (TiO2)260·6H2O and (b) spherical (TiO2)223·18H2O anatase TiO2 nanoparticle models. O and H atoms are shown in white, and Ti atoms are colored according to their coordination pattern: black for Ti6c, green for Ti5c, red for Ti4c, and magenta and cyan for Ti3c–OH and Ti4c–OH, respectively. (c) Comparison between the normalized experimental infrared spectrum of DAP at 0.01 and 100 Pa and the theoretical scaled frequencies of bending and OH stretching for water adsorbates on the (001) and (101) anatase surface facets. (d) Comparison between the normalized experimental infrared spectrum of ST-01 at 0.01 and 100 Pa and the theoretical scaled frequencies of bending and OH stretching for water adsorbates on the spherical anatase nanoparticle model. Black arrows in (c) and (d) highlight the red-shift effect caused by H-bonded water (from red to blue lines) for some selected water adsorbates as depicted in (e,f) on the (001) facet of DAP and in (g,h) on the spherical anatase nanoparticle. The adsorption site and the next-neighboring atoms are evidenced by larger spheres: Ti atoms are colored with the color code mentioned above, H atoms are shown in white, lattice and OH O atoms are in red, and water O atoms are in blue. Relevant H-bonds are represented by thin blue lines, and distances are in angstroms.

Results and Discussion

Titania Nanoparticles

Experiments were performed with three different types of anatase-TiO2 nanoparticles: decahedral anatase particles (DAPs),33 octahedral anatase particles (OAPs),34 and commercially available anatase nanoparticles (ST-01 of Ishihara Sangyo). The crystal structures of these samples were confirmed to be anatase by X-ray diffraction (XRD) (Figure S1). The morphologies of the nanocrystallites were investigated with high-resolution transmission electron microscopy (TEM) (Figure 1). Figure 1a shows a TEM image of DAPs recorded with an electron beam at an incident direction perpendicular to [001] axis; two facets of (101) and (001) were observed in the TEM image of DAPs. OAPs (Figure 1b) show predominantly (101) facets that are thermodynamically most stable. Thus, DAPs and OAPs are well faceted with flat surfaces with low-Miller indices. In contrast, the primary nanoparticles of ST-01 (Figure 1c) are roundish with patches of curved nanosurfaces, hardly showing well-developed flat facets; thus, the surfaces of ST-01 are highly defective and have a large density of low-coordinated sites. The surface areas of the nanoparticles were determined by nitrogen adsorption isotherms at 77 K: 14.7, 230, and 260 m2 g–1 for DAP, OAP, and ST-01, respectively.

Figure 1.

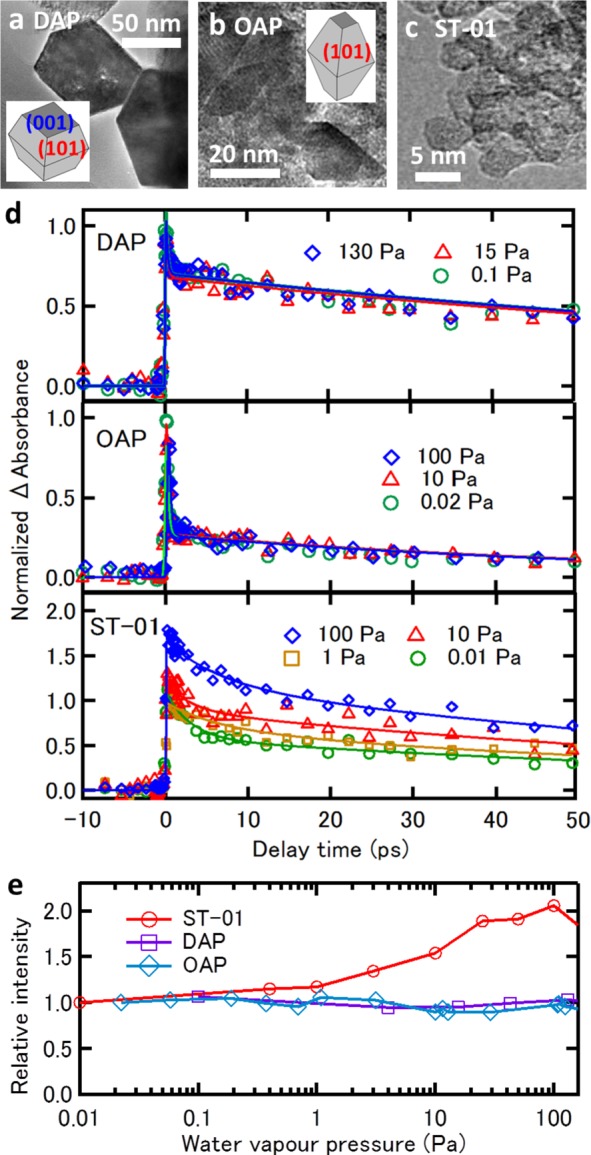
Figure 1

Open in a new tab

TEM images and time profiles of transient absorption anatase-TiO2 nanoparticles. (a) TEM images of DAP, (b) OAP, and (c) ST-01. (d) Time profiles of transient absorption of DAP, OAP, and ST-01 nanoparticles excited with 400 nm pump and probed by 4000 nm probe light at various water vapor pressures. Intensities are normalized at zero delay. (e) Intensities of the slower decay component in the transient absorption profiles as a function of water vapor pressure. Intensities of each sample are normalized at its lowest water vapor pressure.

Transient Absorption Time Profiles

The dynamics of carriers photogenerated in the anatase-TiO2 samples were investigated by measuring time-profiles of transient absorption (TA). The samples were excited with near-ultraviolet pump light at 400 nm (3.1 eV) and probed with mid-infrared probe light at 4000 nm. The pump photon energy is close to the band edge of anatase titania. Photogenerated electrons in the conduction band and in shallow traps have a characteristic absorption band extending from near-IR to mid-IR.16,47 Thus, we can monitor photoelectrons with the IR probe. Figure 1d shows the time profiles of TA as a function of water vapor pressure P in the range of 10–2 < P < 102 Pa. The TA time profiles are composed of a fast (τ = 0.2–3 ps) and a slow (τ = 90–120 ps) decay component. The intensity and the TA decay features of DAP and OAP did not change with P. In contrast, the TA intensity of the slow decay component for ST-01, in particular, significantly increased with P, while the decay features were not sensitive to P. These trends are apparent in Figure 1e where the intensities of the slower decay component are plotted against P.

Photoholes in anatase titania nanoparticles are trapped much faster than photoelectrons;14,48 while the trapping of photogenerated electrons in anatase TiO2 colloidal nanoparticles takes place on a time scale of 260 fs, hole trapping takes place in less than 50 fs.14 This indicates that hole transport from the core to the surface of a nanoparticle is very fast. If hole transport is accelerated due to stabilization of hole at the surface, the loss of electron via electron–hole recombination in the core will decrease. Therefore, the increase in the TA intensity of ST-01 at 4000 nm with increasing P implies that water adsorption enhances the hole trapping ability at the surface of ST-01 nanoparticles.49 Here, we refer to this phenomenon as the water-assisted effect on hole trapping. Note that this effect is reversible in terms of water vapor pressure; thus, no permanent changes in photocatalyst are responsible for this effect. An important question is why the hole trapping probability of ST-01 is strongly enhanced by water adsorption in contrast to DAP and OAP that do not show any enhancement of hole trapping with water adsorption.

DRIFT Spectra

To gain a molecular level insight into the peculiar water-assisted effect, we have measured diffuse reflectance infrared Fourier transform (DRIFT) spectra as a function of water vapor pressure. Figure 2a shows the Kubelka–Munk plots of DRIFT spectra I(P) at P ≈ 0.01 Pa where the intensity is normalized at each of the peak of the hydrogen-bonded OH stretching band. All three titania samples show three prominent absorption bands at 1500–1700, 2600–3650, and 3600–3750 cm–1, which are assignable to H–O–H bending, hydrogen-bonded OH-stretching, and free OH-stretching bands, respectively. Here, we refer to free OH as OH groups of surface hydroxyl or water adsorbate that are not involved in H-bonding. The H–O–H bending band is derived from molecularly adsorbed water, while the latter two bands are contributed from molecularly adsorbed water and surface hydroxyls. The adsorbates responsible for the DRIFT spectra at P ≈ 0.01 Pa are strongly adsorbed species,49 which we call hereafter the A0 species. In fact, some of the species were not completely eliminated by heating the samples to 600 K (Figure S2). Analyzing the temperature dependence of adsorbate coverage under an adsorption–desorption equilibrium49 at 0.01 Pa, we estimated that the adsorption energies of the species are in the range of 1.0–1.9 eV (Figure S2). The most striking difference in the spectra of these samples is that the hydrogen-bonded OH-stretching band of ST-01 is remarkably red-shifted from those of DAP and OAP, peaking at ∼3100 cm–1 (Figure 2a).

Figure 2.

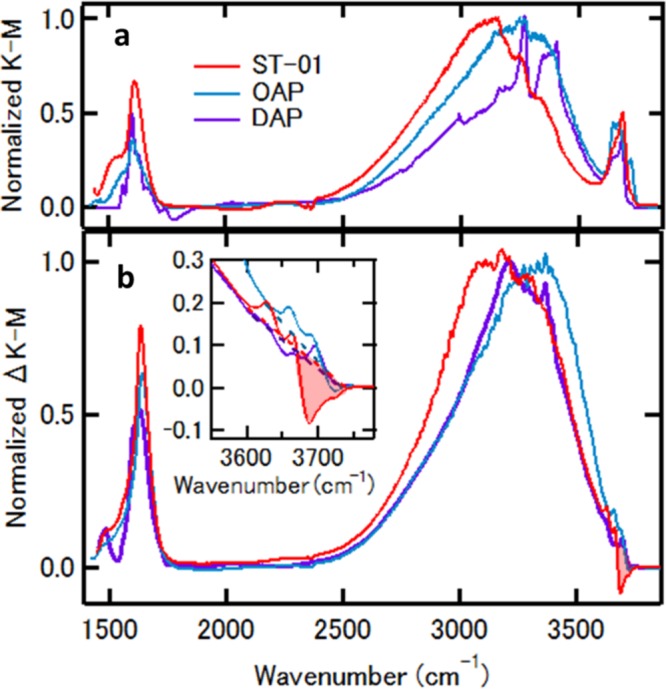
Figure 2

Open in a new tab

DRIFT spectra of the TiO2 nanoparticles. (a) ST-01 (red), OAP (cyan), and DAP (purple), at P ≈ 10–2 Pa, where the intensity is normalized at each peak of the hydrogen-bonded OH-stretching band. (b) Peak normalized difference spectra between 102 and 10–2 Pa. (inset) Enlarged view of the difference spectra in the free OH-stretching band region.

Both the bending band and the hydrogen-bonded OH-stretching band of three samples monotonically grow with increasing water vapor pressure (Figure S3). At P = 100 Pa, the surfaces of these samples are covered with 1 monolayer (ML) of additionally adsorbed water molecules. The difference spectra between 100 and 0.01 Pa are depicted in Figure 2b, where the intensity is normalized at each of the peaks of the hydrogen-bonded OH stretching band. The spectral changes are reversible in terms of water vapor pressure, indicating that the adsorbate responsible for the difference spectra is molecularly adsorbed water. The adsorption energy estimated from pressure dependence is ∼0.7 eV. We refer to the water adsorbate responsible for the difference spectra as the A1 species. In this pressure range, two spectral features characteristic to ST-01 are noteworthy in comparison with DAP and OAP. First, the A1 species on ST-01 nanoparticles also shows the OH-stretching band below ∼3100 cm–1 as in the A0 species. Second, some part of the free OH-stretching band around 3680 cm–1 of ST-01 is depleted upon water adsorption, while such a depletion in the free OH band does not occur in DAP and OAP where an additional water molecule would supply a free OH band with similar frequency (Figure 2b and Figure S4). These findings suggest that surface species with a free OH band on ST-01 nanoparticles are converted to ones showing the significantly red-shifted OH-stretching band below ∼3100 cm–1 by hydrogen bonding with additional water. Because these changes associated with water adsorption occur on the surface of ST-01 but not on those of DAP and OAP, this type of conversion is a key to understanding the mechanism of the water-assisted effect. To elucidate how the observed spectral features are related to the effect of water adsorption on hole trapping ability, we have conducted DFT calculations using faceted and spherical anatase TiO2 nanoparticles.

Vibrational Frequency Analysis

We simulated faceted nanoparticles (DAP and OAP) with the model shown in Figure 3a, while roundish ST-01 nanoparticles having patches of curved nanosurfaces with a spherical nanoparticle are shown in Figure 3b. Some very strongly bound water is present on the surface in the dissociated form to saturate very low-coordinated sites, resulting in terminal OH groups on Ti4c (both in a and b) and Ti3c (only in b), leading to fully stoichiometric systems: (a) (TiO2)260·6H2O (798 atoms) and (b) (TiO2)223·18H2O (723 atoms). We consider this as intrinsic water.

As a next step, we investigate how any additional water would bind to the surface of these nanoparticles. On the faceted ones, water predominantly adsorbs molecularly on the Ti5c on the (101) facets (by −0.91 eV), with very few water molecules dissociating on the Ti4c at the corners of the truncated bipyramid (red in Figure 3a), with a binding energy of −1.39 eV. Dissociative water adsorption also takes place on the (001) facet of DAP, resulting in two surface hydroxyls (Figure 3e), with a binding energy of −2.68 eV. On the spherical ones, a more complex scenario is observed (Figure S5). Water is found to favorably dissociate on Ti3c–OH and Ti4c sites (binding energy from −1.1 to −2.0 eV) and to bind molecularly to Ti4c–OH and Ti5c sites (binding energy from −0.6 to −0.9 eV). However, it is noteworthy that because some Ti5c sites (missing an axial O atom) present a coordination sphere42,50 different from that on regular (101) anatase surface (missing an equatorial O), water dissociation is found to be favored. Finally, further water may bind through H-bonding, either to Ti–OH groups, to Ti–OH2, or to surface bridging O atoms (binding energy in the range between −0.5 and −0.7 eV).

The various types of water binding modes on nanospheres can be associated with A0 and A1 families experimentally observed at low water pressure (0.01 Pa, Figure 2a) and at higher water pressure (100 Pa), based on the computed binding energy (BE) value (Supporting Information section 3): |BE| > 0.7 eV for A0 family and 0.7 eV ≥ |BE| > 0.5 eV for A1 family, respectively.

The calculated vibrational frequencies of several OH and H2O species, dissociatively and molecularly bound on nanoparticle surfaces, are reported in Figure 3c and d for the faceted and round nanoparticles, respectively (Figure S6). The calculated transitions very well fit the experimental spectra observed at 0.01 and 100 Pa of ST-01 and DAP. The frequency of free OH stretching is sensitive to the coordination number of the binding surface Ti ion and the O–Ti–OH torsional angle (Figure S7).

It is noteworthy that large red-shifts are computed when relatively strong H-bonding takes place, either with surface O atoms or with additional water molecules on the surface of nanosphere. In particular, after H-bonding with additional water, the stretching frequencies of free terminal OH at low coordination sites around 3680 cm–1 shift to values below 3100 cm–1 (Figure 3d), in excellent agreement with the difference IR spectrum in Figure 2b. Those characterized by the large red-shifts in the OH stretching frequency are represented by ball-and-stick models before and after H-bonding with an additional water molecule, in Figure 3g and h, respectively, where the curved surface provides the local structures around terminal OHs that allow one to align the OH···O(H2) bond almost linearly, which strengthens this hydrogen bond. A correlation between H-bond distance and red-shift extent is well-known and shown for the present study in Figure S8. Note that OH groups can only form a strong H-bond with additional water molecules because of the short Ti–OH bond that does not allow for large flexibility for forming H-bond with other distant surface hydroxyl groups, contrary to the case of Ti–OH2. In contrast, although free OHs exist on a (001) facet of DAP as a result of dissociative adsorption of water (Figure 3e), the red-shift in the OH stretching frequency upon water coordination (Figure 3f) is much smaller than those observed for nanospheres (see Figure 3c) because the faceted surface forces the OH···O(H2) bond to be bent, which weakens the hydrogen bond. Thus, calculations show that the OH species whose frequency is significantly red-shifted by H-bonding with additional water only exists on nanospheres.

Hole Trapping Mechanism

Excitation of TiO2 nanoparticles with light induces the formation of excitons, typically, one per nanoparticle. If the electron–hole pair does not recombine and there is sufficient thermal energy to overcome the tiny exciton binding energy, the electron and hole separate. There is a preference for the hole to travel from the bulk to the surface, and we have found that the best surface-trapping site is a bridging O2c ion.50 Free OH species are very poor hole trapping sites. Therefore, in vacuum conditions, where only very strongly bound water and surface hydroxyl are present, holes are expected to be trapped at O2c sites, in the cases of both faceted and spherical nanoparticles.

At increasing water partial pressure, the water-assisted hole trapping effect is not observed for faceted nanoparticles (Figure 1e). There are several reasons for that. First, on Ti5c ions at (101) facets, water does not dissociate but only adsorbs as molecular species (Figure S9). The latter are not capable of hole trapping, and not even hole-induced water dissociation occurs because this process was found to be endothermic by 0.32 eV (Figure S10), in line with a previous study.26 Second, molecularly adsorbed water on (101) facets in aqueous environment was shown to inhibit hole trapping by O2c centers because they accept H-bonds from water.26 Thus, the absence in the water-assisted effect implies that hole trapping ability of O2c is compensated by subsurface O3c. Third, water can be dissociatively adsorbed on (001) facets widely distributed on DAP surface. We modeled water dissociation on Ti5c, as previously observed,51,52 by forming two OH groups (Figure 3e). Hole trapping at such OH species requires breaking of the H-bond between them. For this reason, they are not good trapping sites, being less stable by +0.34 eV with respect to hole trapped on a (001) surface O2c. The effect of additional H-bonded water is even more detrimental, increasing the energy instability to +0.42 eV (Figure S11c and d).

Differently from faceted, the water-assisted effect is observed on roundish ST-01 by the increase in the TA intensity of slow component. In the following, we will explain why. First, water dissociates on Ti3c, Ti4c, and some Ti5c sites (missing an axial O) on nanosphere. Strongly bound isolated OH groups are thus formed on the surface (A0 species), which are capable of hole trapping, although they are worse than O2c surface sites (by +0.50 eV). Yet, here the role of additional water (A1 species) comes into play: additional water assists the process of hole trapping on OH species and improves it, resulting in a larger hole trapping energy.

A clue that OH species are involved in the underlying mechanism for the water-assisted effect on ST-01 comes from the difference spectrum in Figure 2b, where a depletion in the free OH band and an increase in the H-bonded one are observed. As shown in Figure 4a, calculations proved that water may assist hole trapping both (i) by coordinating as an additional ligand to the low-coordinated Ti ion in the Ti3c–OH or Ti4c–OH trapping species and (ii) by binding to the OH trapping species through quite strong H-bonding, which is responsible for a large red-shift in the OH stretching frequency.

Figure 4.

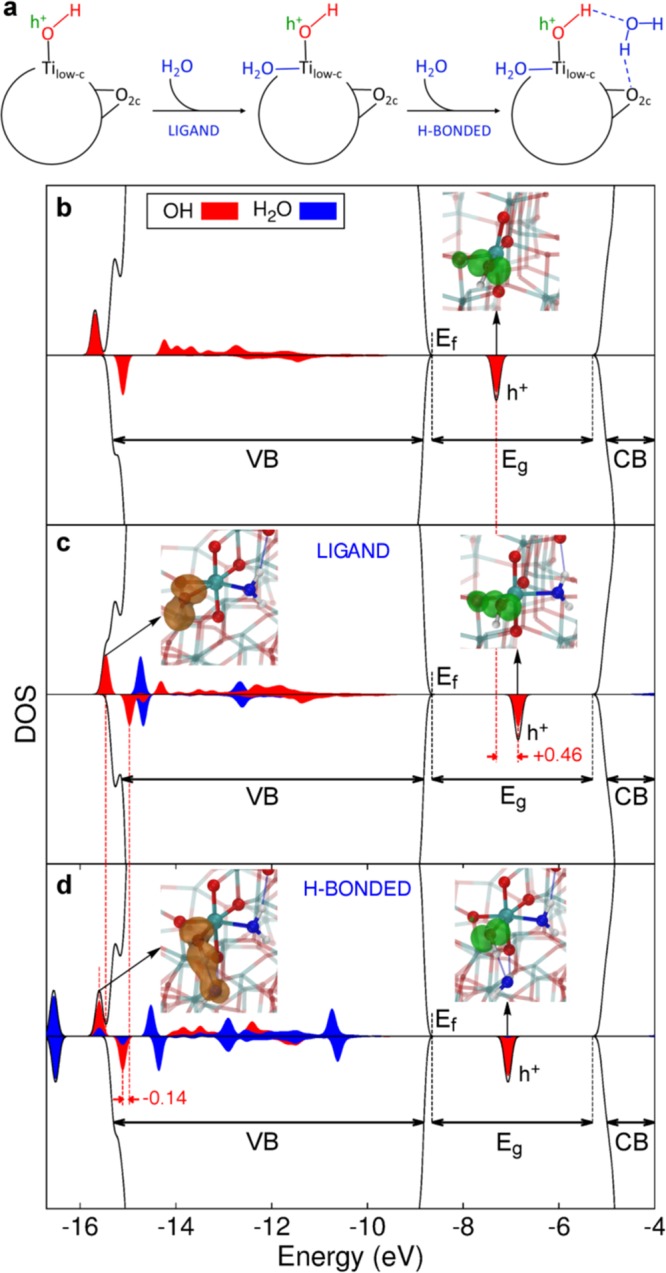
Figure 4

Open in a new tab

Enhancement of hole trapping at surface hydroxyls by hydrogen bonding with water. (a) Schematic representation of the water adsorption on TiO2 nanospheres. For low coverages (A0), water dissociatively adsorbs on low coordinated Ti sites (Tilow–c) creating OH groups, which are not good trapping sites. At higher coverages (A1) water assists the hole trapping process by first coordinating as a ligand to the Ti low-coordinated sites and then by H-bonding to the OH species and to the surface O atoms. (b) Simulated total (black) and projected (red and blue) density of states of the spherical anatase nanoparticle with an excess hole in the Ti4c–OH site and (c) in the same site with an additional ligand water molecule, and (d) with both an additional ligand and H-bonded water molecules. Dashed red lines are traced in correspondence to the hole state in (b) and (c) and in correspondence of the OH bonding states in (c) and (d). Energy shifts are in eV. In the insets on the right of (b, c) and (d), the 3D spin density (in green), representing the OH radical formed upon hole trapping, is given with an isovalue of 0.01 au. In the left insets of (c) and (d) the alpha OH bonding state is represented with a |Ψ|2 3D plot (in orange) with an isovalue of 0.005 au. Next-neighboring atoms are evidenced by larger spheres: Ti atoms are colored in cyan, H atoms in white, lattice and OH O atoms in red, water O atoms in blue. Relevant H-bonds are represented by thin blue lines.

Water coordination as an additional ligand to complete the coordination sphere of a Ti3c–OH was found to enable its hole trapping ability, and in the case of a Ti4c–OH to enhance it by −0.36 eV. The reason is that the water ligand brings further electronic charge to the Ti ion, resulting in a more electron-rich OH species (3a1 of water → dx2–y2 of Ti → O 2p of OH) and thus a better hole trap. This is evidenced also by a shift in energy of the empty (hole) state in the gap by +0.46 eV (compare Figure 4b with c), indicating a hole stabilization: the higher is the hole state, the better is the trapping.

A strong H-bonding of water to the OH group favors hole trapping by about −0.15 eV, by forming a bonding state between the σ OH of the Ti–OH species and the 3a1 molecular orbital of H2O (brown lobes in Figure 4d); this causes electron transfer from H2O to OH through the H-bond and an evident elongation of the O–H bond length by 0.06 Å. By comparing the projected density of states (PDOS) in Figure 4d with that in Figure 4c, we notice that the H-bonded water stabilizes the OH states (red projections in the range of energy between −15/–16 eV) at the bottom or below the valence band. The PDOS clearly shows the position of the empty hole (h+) state in the gap, and that is fully localized on the O 2p state (red projection is almost fully covering the hole peak). Therefore, the electron transfer through the strong H-bonding with the additional water molecule accompanied by the elongation of terminal OH bond stabilizes and localizes the hole on the O atom of terminal OH.

Regarding the effect of a strong H-bond with additional water described above, we must consider another aspect to induce successful water-assisted hole trapping. This second crucial factor becomes clear if we compare a surface hydroxyl on a nanosphere with one on a DAP (001) facet (Figure 5). A surface hydroxyl forms a flexible H-bond network including an additional water molecule that is highly affected by hole trapping at OH. Going from the neutral to the hole trapped charged system, that is, from left to right of Figure 5 (b,c for nanosphere and d,e for (001) surface), two opposite effects clearly emerge: in the case of nanospheres (blue curve in Figure 5a), we observe an enhanced stabilization of the system upon hole trapping as a consequence of the strengthening of the H-bond network (see shorter distances in Figure 5c with respect to Figure 5b); whereas, in the case of DAP, we observe a reduced stabilization by water as a consequence of a reduced number of H-bonds. The neutral state of the terminal OH is stabilized through H-bonds with the neighboring OH and the additional water. Upon hole trapping, the terminal OH can no longer donate charge to the neighboring OH, thus breaking the H-bond, but making a stronger and more directional H-bond with the additional water molecule. This lifts the water molecule from the surface with no possibility of establishing H-bonds with O2c sites. Thus, a significant difference between spherical and faceted nanocrystallites is in the local structures around low-coordinated Ti–OH sites provided only by the curved surface of nanospheres, where an additional water molecule can form robust H-bonds to both the terminal OH and substrate O2c in the neutral state, and their robustness is further enhanced in the charged state. Consequently, we learn that for spherical nanoparticles there is a positive overall structural reorganization energy following hole trapping, in contrast with a negative effect in the case of the (001) surface of faceted nanocrystallites. Therefore, the curved surface not only provides low-coordinated Ti–OH sites but also the local surrounding structures suitable for the robust H-bonds around them.

Figure 5.

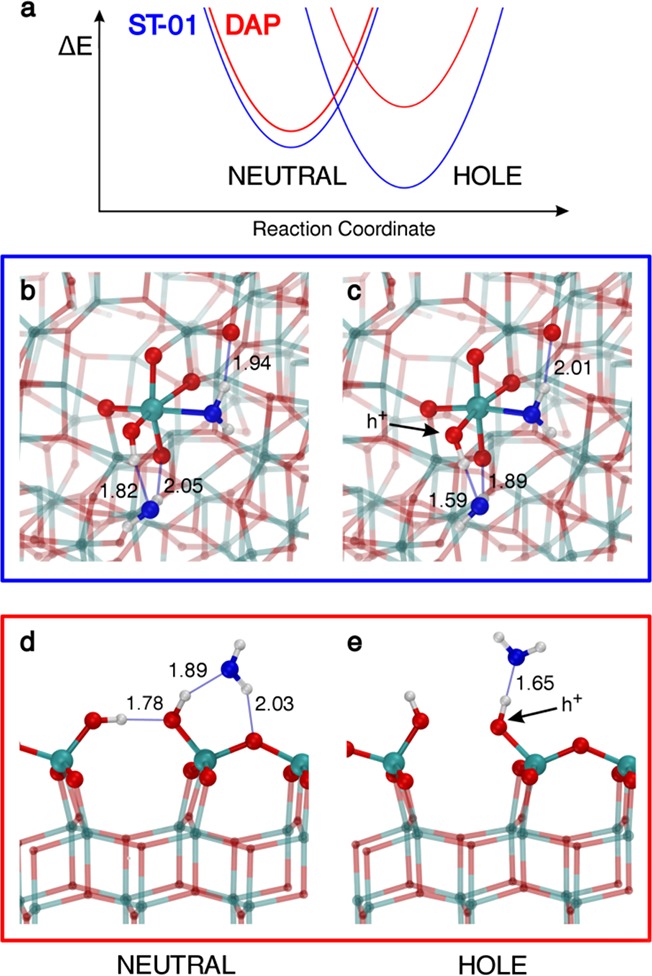
Figure 5

Open in a new tab

Hydrogen-bonding rearrangement after hole trapping. (a) Schematic representation of the water stabilization energy (ΔE) of the system before and after hole trapping for the spherical TiO2 nanoparticle (blue line) and the faceted one (red line). Ball-and-stick model of a hydroxyl on a Tilow-c with an additional H-bonded water molecule on the spherical nanoparticle and the (001) surface before (b,d) and after (c,e) hole trapping at the OH group. Next-neighboring atoms are evidenced by larger spheres: Ti atoms are colored in cyan, H atoms are in white, lattice and OH O atoms are in red, and water O atoms are in blue. Relevant H-bonds are represented by thin blue lines, and distances are in angstroms.

Conclusions

This combined experimental and theoretical study provides a comprehensive picture of the hole trapping mechanism at the surface of anatase TiO2 nanoparticles of different shape (faceted vs spherical) and in the presence of gradually increasing water adsorbates: water adsorbates enhance the hole trapping ability of spherical nanoparticles, but do not influence that of faceted ones. The models used for the hybrid DFT calculations are very large (∼800 atoms) to be as close as possible to experiments. Hydroxyl groups on low-coordinated Ti sites (Ti4c–OH and Ti3c–OH), resulting from water dissociation, are abundant on spherical nanoparticles, whereas they are very scarce on faceted surfaces. Moreover, the curved surface of nanospherical particles can provide a local surrounding structure to the terminal OH where robust H-bonds are created with additional water adsorbates, resulting in substantially red-shifted OH stretching bands. The first shell of water coordination is found to play a crucial role in enhancing the trapping ability either by binding as a ligand to the low-coordinated Ti site or by hydrogen bonding directly to the trapping OH (Figure 4a). The fact that the hole trapping ability of the low-coordinated Ti–OH sites is triggered by interactions with water molecules proves that they are active species in realistic aqueous operation conditions. Consequently, the morphology-dependent water-assisted hole trapping effect clarified by the current study not only leads to a molecular-level understanding of water oxidation with metal oxides, but also provides a new insight into the strategy of surface engineering for high performance photocatalysts.

Acknowledgments

This work was supported by a Grant-in-Aid for Scientific Research (A) (Grant no. 16H02249), for Young Scientists (A) (Grant no. 16H06029) from the Japanese Society for the Promotion of Sciences, by a Grant-in-Aid for Scientific Research on Innovative Areas of MEXT (Grant no. 16H00937), and has received funding from the European Research Council (ERC) under the European Union’s HORIZON2020 research and innovation programme (ERC Grant Agreement no. 647020).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b11061.

  • Characterization of samples by XRD patterns and DRIFT spectra, computational details, binding energies and vibrational frequencies of water adsorbates, and hole trapping ability of adsorbates on Ti cation (PDF)

Author Contributions

# K.S. and G.F. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

ja7b11061_si_001.pdf (2.3MB, pdf)

References

  1. Linsebigler A. L.; Lu G.; Yates J. T. Jr. Chem. Rev. 1995, 95, 735–758. 10.1021/cr00035a013. [DOI] [Google Scholar]
  2. Diebold U. Surf. Sci. Rep. 2003, 48, 53–229. 10.1016/S0167-5729(02)00100-0. [DOI] [Google Scholar]
  3. Thompson T.; Yates J. T. Jr. Chem. Rev. 2006, 106, 4428–4453. 10.1021/cr050172k. [DOI] [PubMed] [Google Scholar]
  4. Fujishima A.; Zhang X.; Tryk D. A. Surf. Sci. Rep. 2008, 63, 515–582. 10.1016/j.surfrep.2008.10.001. [DOI] [Google Scholar]
  5. Henderson M. A. Surf. Sci. Rep. 2011, 66, 185–297. 10.1016/j.surfrep.2011.01.001. [DOI] [Google Scholar]
  6. Berger T.; Sterrer M.; Stankic S.; Bernardi J.; Diwald O.; Knözinger E. Mater. Sci. Eng., C 2005, 25, 664–668. 10.1016/j.msec.2005.06.013. [DOI] [Google Scholar]
  7. Panarelli E. G.; Livraghi S.; Maurelli S.; Polliotto V.; Chiesa M.; Giamello E. J. Photochem. Photobiol., A 2016, 322–323, 27–34. 10.1016/j.jphotochem.2016.02.015. [DOI] [Google Scholar]
  8. Micic O.; Zhang Y.; Cromack K. R.; Trifunac A.; Thurnauer M. J. Phys. Chem. 1993, 97, 13284–13288. 10.1021/j100152a036. [DOI] [Google Scholar]
  9. Brezová V.; Barbieriková Z.; Zukalová M.; Dvoranová D.; Kavan L. Catal. Today 2014, 230, 112–118. 10.1016/j.cattod.2013.11.026. [DOI] [Google Scholar]
  10. Rothenberger G.; Moser J.; Grätzel M.; Serpone N.; Sharma D. K. J. Am. Chem. Soc. 1985, 107, 8054–8059. 10.1021/ja00312a043. [DOI] [Google Scholar]
  11. Kamat P. V.; Bedja I.; Hotchandani S. J. Phys. Chem. 1994, 98, 9137–9142. 10.1021/j100088a008. [DOI] [Google Scholar]
  12. Colombo D. P. Jr.; Roussel K. A.; Saeh J.; Skinner D. E.; Cavaleri J. J.; Bowman R. M. Chem. Phys. Lett. 1995, 232, 207–214. 10.1016/0009-2614(94)01343-T. [DOI] [Google Scholar]
  13. Furube A.; Asahi T.; Masuhara H.; Yamashita H.; Anpo M. J. Phys. Chem. B 1999, 103, 3120–3127. 10.1021/jp984162h. [DOI] [Google Scholar]
  14. Yang X.; Tamai N. Phys. Chem. Chem. Phys. 2001, 3, 3393–3398. 10.1039/b101721g. [DOI] [Google Scholar]
  15. Iwata K.; Takaya T.; Hamaguchi H.-O.; Yamakata A.; Ishibashi T.-A.; Onishi H.; Kuroda H. J. Phys. Chem. B 2004, 108, 20233–20239. 10.1021/jp047531k. [DOI] [Google Scholar]
  16. Yoshihara T.; Katoh R.; Furube A.; Tamaki Y.; Murai M.; Hara K.; Murata S.; Arakawa H.; Tachiya M. J. Phys. Chem. B 2004, 108, 3817–3823. 10.1021/jp031305d. [DOI] [Google Scholar]
  17. Tamaki Y.; Furube A.; Murai M.; Hara K.; Katoh R.; Tachiya M. J. Am. Chem. Soc. 2006, 128, 416–417. 10.1021/ja055866p. [DOI] [PubMed] [Google Scholar]
  18. Tamaki Y.; Furube A.; Murai M.; Hara K.; Katoh R.; Tachiya M. Phys. Chem. Chem. Phys. 2007, 9, 1453–1460. 10.1039/B617552J. [DOI] [PubMed] [Google Scholar]
  19. Tamaki Y.; Hara K.; Katoh R.; Tachiya M.; Furube A. J. Phys. Chem. C 2009, 113, 11741–11746. 10.1021/jp901833j. [DOI] [Google Scholar]
  20. Antila L. J.; Santomauro F. G.; Hammarstrom L.; Fernandes D. L. A.; Sá J. Chem. Commun. 2015, 51, 10914–10916. 10.1039/C5CC02876K. [DOI] [PubMed] [Google Scholar]
  21. Litke A.; Su Y.; Tranca I.; Weber T.; Hensen E. J. M.; Hofmann J. P. J. Phys. Chem. C 2017, 121, 7514–7524. 10.1021/acs.jpcc.7b00472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. De Angelis F.; Di Valentin C.; Fantacci S.; Vittadini A.; Selloni A. Chem. Rev. 2014, 114, 9708–9753. 10.1021/cr500055q. [DOI] [PubMed] [Google Scholar]
  23. Selcuk S.; Selloni A. Nat. Mater. 2016, 15, 1107–1112. 10.1038/nmat4672. [DOI] [PubMed] [Google Scholar]
  24. Di Valentin C.; Pacchioni G.; Selloni A. Phys. Rev. Lett. 2006, 97, 166803. 10.1103/PhysRevLett.97.166803. [DOI] [PubMed] [Google Scholar]
  25. Di Valentin C.; Selloni A. J. Phys. Chem. Lett. 2011, 2, 2223–2228. 10.1021/jz2009874. [DOI] [Google Scholar]
  26. Chen J.; Li Y.-F.; Sit P.; Selloni A. J. Am. Chem. Soc. 2013, 135, 18774–18777. 10.1021/ja410685m. [DOI] [PubMed] [Google Scholar]
  27. Di Valentin C. J. Phys.: Condens. Matter 2016, 28, 074002. 10.1088/0953-8984/28/7/074002. [DOI] [PubMed] [Google Scholar]
  28. Rajh T.; Dimitrijevic N. M.; Bissonnette M.; Koritarov T.; Konda V. Chem. Rev. 2014, 114, 10177–10216. 10.1021/cr500029g. [DOI] [PubMed] [Google Scholar]
  29. Miccio L. A.; Setvin M.; Müller M.; Abadía M.; Piquero I.; Lobo-Checa J.; Schiller F.; Rogero C.; Schmid M.; Sánchez-Portal D.; Diebold U.; Ortega J. E. Nano Lett. 2016, 16, 2017–2022. 10.1021/acs.nanolett.5b05286. [DOI] [PubMed] [Google Scholar]
  30. Yang S.; Yang B. X.; Wu L.; Li Y. H.; Liu P.; Zhao H.; Yu Y. Y.; Gong X. Q.; Yang H. G. Nat. Commun. 2014, 5, 5355. 10.1038/ncomms6355. [DOI] [PubMed] [Google Scholar]
  31. Zhang J.; Wu B.; Huang L.; Liu P.; Wang X.; Lu Z.; Xu G.; Zhang E.; Wang H.; Kong Z.; Xi J.; Ji Z. J. Alloys Compd. 2016, 661, 441–447. 10.1016/j.jallcom.2015.11.225. [DOI] [Google Scholar]
  32. Wu H.; Li H.; Li J.; Lu B.; Yang Y.; Yuan W.; Wang Y.; Zhang Z. CrystEngComm 2015, 17, 7254–7257. 10.1039/C5CE01283J. [DOI] [Google Scholar]
  33. Wei Z.; Kowalska E.; Ohtani B. Chem. Lett. 2014, 43, 346–348. 10.1246/cl.130985. [DOI] [Google Scholar]
  34. Amano F.; Prieto-Mahaney O.-O.; Terada Y.; Yasumoto T.; Shibayama T.; Ohtani B. Chem. Mater. 2009, 21, 2601–2603. 10.1021/cm9004344. [DOI] [PubMed] [Google Scholar]
  35. Bunsho O.; Prieto M. O. O.; Fumiaki A.; Naoya M.; Ryu A. J. Adv. Oxid. Technol. 2016, 13, 247–261. [Google Scholar]
  36. Kakuma Y.; Nosaka A. Y.; Nosaka Y. Phys. Chem. Chem. Phys. 2015, 17, 18691–18698. 10.1039/C5CP02004B. [DOI] [PubMed] [Google Scholar]
  37. Nosaka A. Y.; Fujiwara T.; Yagi H.; Akutsu H.; Nosaka Y. J. Phys. Chem. B 2004, 108, 9121–9125. 10.1021/jp037297i. [DOI] [PubMed] [Google Scholar]
  38. Yabuta M.; Takayama T.; Shirai K.; Watanabe K.; Kudo A.; Sugimoto T.; Matsumoto Y. J. Phys. Chem. C 2014, 118, 10972–10979. 10.1021/jp502775y. [DOI] [Google Scholar]
  39. Dovesi R.; Saunders V. R.; Roetti C.; Orlando R.; Zicovich-Wilson C. M.; Pascale F.; Civalleri B.; Doll K.; Harrison N. M.; Bush I. J.; D‘Arco P.; Llunell M.; Causà M.; Noël Y.. CRYSTAL14 User’s Manual; 2014. [Google Scholar]
  40. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  41. Becke A. D. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  42. Fazio G.; Ferrighi L.; Di Valentin C. J. Phys. Chem. C 2015, 119, 20735–20746. 10.1021/acs.jpcc.5b06384. [DOI] [Google Scholar]
  43. Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 7260–7268. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
  44. Luschtinetz R.; Frenzel J.; Milek T.; Seifert G. J. Phys. Chem. C 2009, 113, 5730–5740. 10.1021/jp8110343. [DOI] [Google Scholar]
  45. Aradi B.; Hourahine B.; Frauenheim T. J. Phys. Chem. A 2007, 111, 5678–5684. 10.1021/jp070186p. [DOI] [PubMed] [Google Scholar]
  46. Shimanouchi T.Tables of Molecular Vibrational Frequencies Consolidated; NSRDS-NBS 39; National Bureau of Standards, 1972; Vol. 1, pp 1–160. [Google Scholar]
  47. Yamakata A.; Ishibashi T.-A.; Onishi H. J. Phys. Chem. B 2001, 105, 7258–7262. 10.1021/jp010802w. [DOI] [Google Scholar]
  48. Shen Q.; Katayama K.; Sawada T.; Yamaguchi M.; Kumagai Y.; Toyoda T. Chem. Phys. Lett. 2006, 419, 464–468. 10.1016/j.cplett.2005.11.109. [DOI] [Google Scholar]
  49. Shirai K.; Sugimoto T.; Watanabe K.; Haruta M.; Kurata H.; Matsumoto Y. Nano Lett. 2016, 16, 1323–1327. 10.1021/acs.nanolett.5b04724. [DOI] [PubMed] [Google Scholar]
  50. Fazio G.; Ferrighi L.; Di Valentin C. Nano Energy 2016, 27, 673–689. 10.1016/j.nanoen.2016.08.003. [DOI] [Google Scholar]
  51. Selcuk S.; Selloni A. J. Phys. Chem. C 2013, 117, 6358–6362. 10.1021/jp402100v. [DOI] [Google Scholar]
  52. Gong X.-Q.; Selloni A. J. Phys. Chem. B 2005, 109, 19560–19562. 10.1021/jp055311g. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja7b11061_si_001.pdf (2.3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES