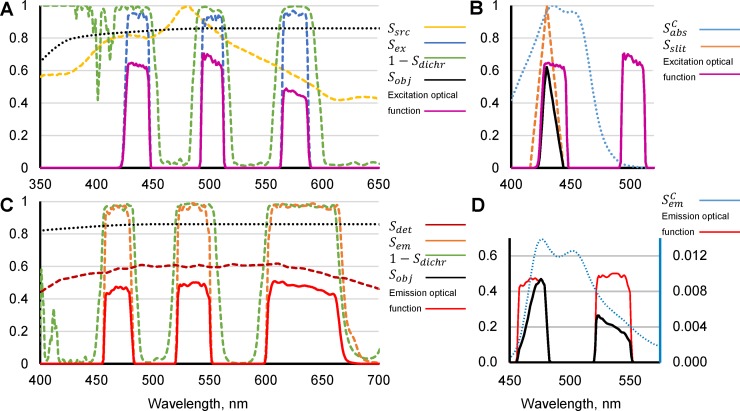
Fig 1. Parameters necessary for calculation of ratio factor A for Cerulean and Venus fluorescent proteins.
(A) Spectra of the optical components in the excitation path of the imaging system. Ssrc(λ), Sex(λ), Sdichr(λ), Sobj(λ) are spectra for the light source (Polychrome V monochromator, TILL Photonics, yellow), excitation filter (Chroma 69008x, blue), dichroic mirror (Chroma 69008bs, green) and objective (Olympus UAPO 40XOI3/340, black), respectively, mounted on Olympus IX71 microscope. Point-by-point multiplication of spectra for each optical element yields an optical function of microscope excitation light path shown by a violet trace. This excitation optical function of the particular imaging system can be used for calculation of a ratio factor A for a wide range of different fluorescent labels. (B) Further point-by-point multiplication of the optical function (violet), normalized Cerulean absorption spectrum (blue), and a spectrum of monochromator slit chosen for a given experiment (orange) gives a function of excitation path for Cerulean (black). Integration of this function and multiplication by the extinction coefficient for Cerulean absorbance results in , necessary for estimation of the ratio factor A (see Eq 1). (C) Spectra of the optical components in the emission path of the imaging system. Sobj(λ),Sdichr(λ),Sem(λ),Sdet(λ) are objective (Olympus UAPO 40XOI3/340, black), dichroic mirror (Chroma 69008bs, green), and emission filter (Chroma 69008m, dotted red) transmittance and detector (QImaging ExiBlue, brown) sensitivity, respectively. Point-by-point multiplication of spectra for each optical element gives an optical function of microscope emission path shown by a red bold trace. This emission optical function of the particular imaging system can be used for calculation of a ratio factor A for a wide range of different fluorescent labels. (D) Further point-by-point multiplication of the optical function (red dashed trace; left Y axes) and Cerulean emission spectrum, integral of which is normalized to 1, (blue dashed trace; right Y axes) gives the function of emission path for Cerulean (black trace, right Y axes). Integration of this function and multiplication by Cerulean quantum yield results in .