Skip to main content
. 2018 Apr 5;7:e33549. doi: 10.7554/eLife.33549

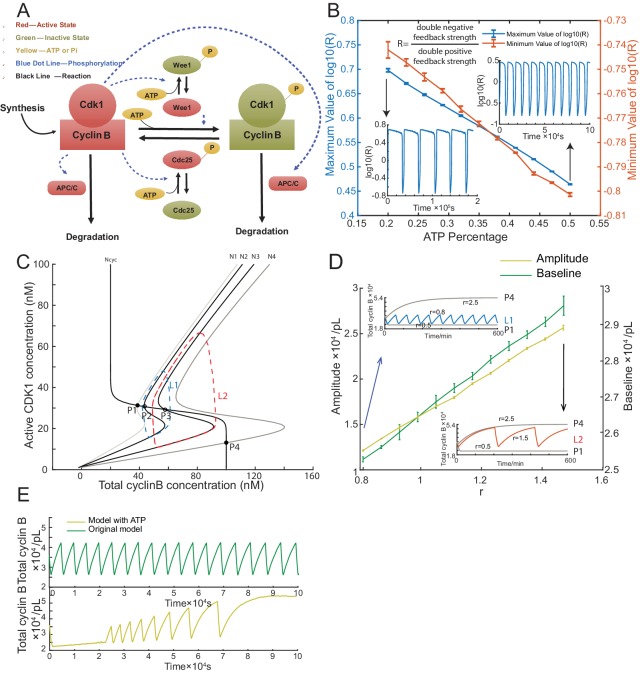
Figure 3. Simulation of cell cycle model with energy depletion.

(A) Schematic view of the cyclin B-Cdk1 oscillation system. Note that ATP is taken into consideration. Activated molecules are marked in red, inactivated molecules in green and ATP or Pi in yellow. Black line indicates a reaction and blue dotted line a phosphorylation. (B) Relationship between ATP percentage and R value, showing that decreasing the ATP concentration leads to a higher R value. Error bars represent ranges from three simulations. Two inserts represent the dynamics of R value over time when the ATP percentage [ATP]/([ATP]+[ADP]) is set as 0.2 (left) and 0.5 (right). The model is simulated using Gillespie algorithm. (C) Phase plots of the two-ODE model. Parameters for the cyclin B nullcline (Ncyc) (Yang and Ferrell, 2013) and the Cdk1 nullclines with a variety of values of r (N1, r = 0.5; N2, r = 0.8; N3, r = 1.5; N4, r = 2.5) were chosen based on previous experimental work (Pomerening et al., 2003; Sha et al., 2003). Note that the r here is a parameter and is different from R in Figure 3B. Two sample traces of limit cycle oscillations are plotted for r = 0.8 (L1) and r = 1.5 (L2), showing that a larger r value leads to a higher amplitude and baseline. In addition, r = 0.5 (N1) generates a low stable steady-state of cyclin B (P1), while r = 2.5 (N4) a high stable steady-state of cyclin B (P4). These stable steady-states are indicated by the intersections of the nullclines (filled circles). The unstable steady states are labeled with open circles (P2 and P3). (D) Relationship between the oscillation baseline and amplitude values and ATP concentration (positively correlated with r). Error bars indicate the ranges of 3 replicates. Inserts show two example time courses of total cyclin B with different r values (L1, r = 0.8; L2, r = 1.5), colors of which match the ones in Figure 3C. Simulation is done using Gillespie algorithm. (E) Time series of total cyclin B molecules from the model without ATP (top panel, green line) and with ATP (bottom panel, yellow line).

Figure 3—source data 1. Simulated data for generating Figure 3—figure supplement 1 using the energy depletion model.
elife-33549-fig3-data1.csv (95.2KB, csv)
DOI: 10.7554/eLife.33549.011

Figure 3.

Figure 3—figure supplement 1. Analysis of the dependence of oscillations on the cyclin B synthesis and degradation rates.

Figure 3—figure supplement 1.

(A) The period of the first cycle vs the last cycle in a droplet, showing that the period of the last cycle tends to be longer. Blue line indicates the same first and last periods. (B) Pearson correlation between the period of cycle and the index of cycle in a droplet. Positive correlation indicates that the cell cycle period tends to increase over time. (C) The period and number of oscillations decrease with an increasing cyclin B synthesis rate. Error bars represent standard deviations from 50 simulations. (D) Effects of synthesis and degradation rates of cyclin B as well as r on the baseline and amplitude of oscillations of total cyclin B. Color bar indicates baseline or amplitude of cyclin B (number of molecules per pL).