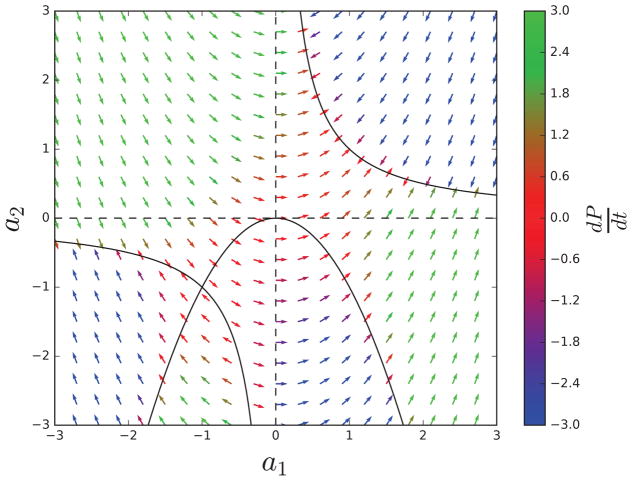
Figure 11.

Vector field for the 𝒜[1, 1, 1] linear case with c₁ = 1, α = 1, and β = 1. a₁ correspond to the horizontal axis and a₂ correspond to the vertical axis. The critical points correspond to the two hyperbolas, and all critical points are fixed points and global minima of the error functions. Arrows are colored according to the value of dP/dt, showing how the critical points inside the parabola $a_2=-a_1^2/c_1$ are unstable. All other critical points are attractors. Reversing the sign of α, leads to a reflection across the a₂-axis; reversing the sign of c₁, leads to a reflection across both the a₁ and a₂ axes.