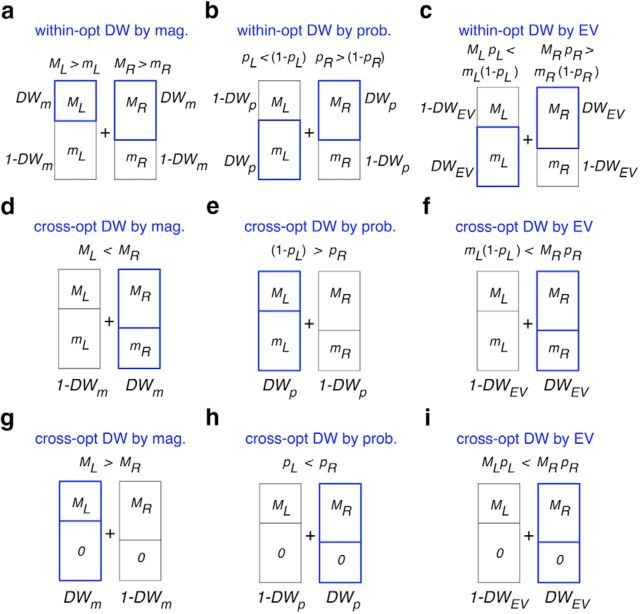
Figure 2.
Alternative models for DW. a–c, Alternative DW between the two outcomes of each gamble (within-option) in the token-gambling task with two nonzero reward outcomes. a–c show three mechanisms for how magnitudes and probabilities of the two possible gamble outcomes can influence the weight of each gamble outcome on the overall gamble value: DW by magnitude (a); DW by probability (b); and DW by EV (c). In all panels, ML and pL indicate the magnitude and probability associated with the left gamble's larger magnitude outcome, respectively, and mL is the magnitude of the other left gamble outcome (the probability of this outcome is 1 − pL). The same convention is used for the right gamble. The blue box shows the outcome that is assigned with a larger weight based on a given mechanism. The DW factors determine the strength of DW according to the reward magnitude (DWm), reward probability (DWp), and EV (DWEV) of the two outcomes. d–f, Alternative DW between better outcomes of the two alternative gambles (cross-option) in the token-gambling task with two nonzero reward outcomes. d–f show three mechanisms for how magnitudes and probabilities of the better outcome of the two alternative gambles can modulate their values: cross-option DW by magnitude (d), cross-option DW by probability (e), and cross-option DW by EV (f). The blue box shows the gamble that is assigned with a larger weight based on a given mechanism. The DW factors determine the strength of DW according to the reward magnitude (d), the reward probability (e), and EV of the two gambles (f). g–i, Alternative cross-option DW between nonzero outcomes of the two alternative gambles in the juice-gambling task. g–i show three mechanisms for how magnitudes and probabilities of the nonzero outcome of the two alternative gambles can modulate their values. Importantly, as shown in Figure 2-1 and Figure 2-2, our fitting method is able to identify correctly the model used to generate a given set of data and thus can distinguish between the alternative models.