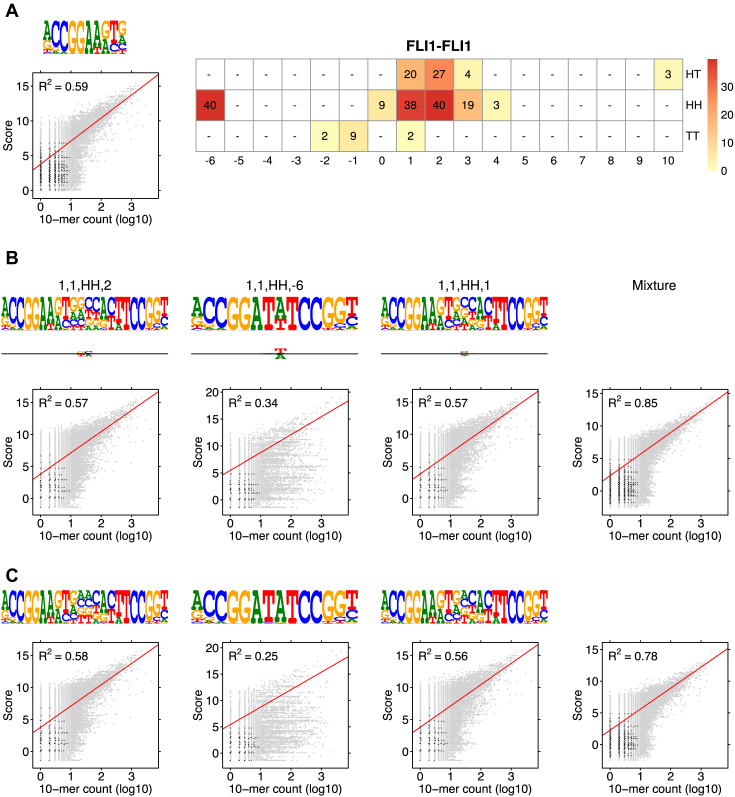
Figure 6.
Modularity analysis of the binding motifs of FLI1. (A) The monomer model (λ1 = 0.08) and the COB table in units of integer multiples of 0.001. Also shown is the correlation analysis using only the monomer model. (B) Correlation analysis of the model learned for FLI1 by MODER: the monomer model and six dimeric PPMs τ1, 1, HH, 2, τ1, 1, HH, −6, τ1, 1, HH, 1, τ1, 1, HT, 2, τ1, 1, HT, 1, τ1, 1, HH, 3 (only three best are shown in the Figure) were included in the analysis by the 85% rule. Deviation matrices are depicted below the logos of the dimeric PPMs. The mixture of the PPMs uses weights λ = 0.080, 0.040, 0.040, 0.038, 0.027, 0.020, 0.019. (C) Correlation analysis as in B but for the expected PPMs E1, 1, HH, 2, E1, 1, HH, −6, E1, 1, HH, 1, E1, 1, HT, 2, E1, 1, HT, 1, E1, 1, HH, 3 under the independence assumption. The R2-values for the learned and expected PPMs differ clearly for the mixture and the dimeric case HH –6. The purely modular model cannot handle the dimeric case HH –6 properly, since expected PPMs are always palindromic for orientations HH and TT, while here the learned model HH –6 turns out to be directed. Albeit quite weak, the directionality has a clear effect on R2.