Fig. 1.

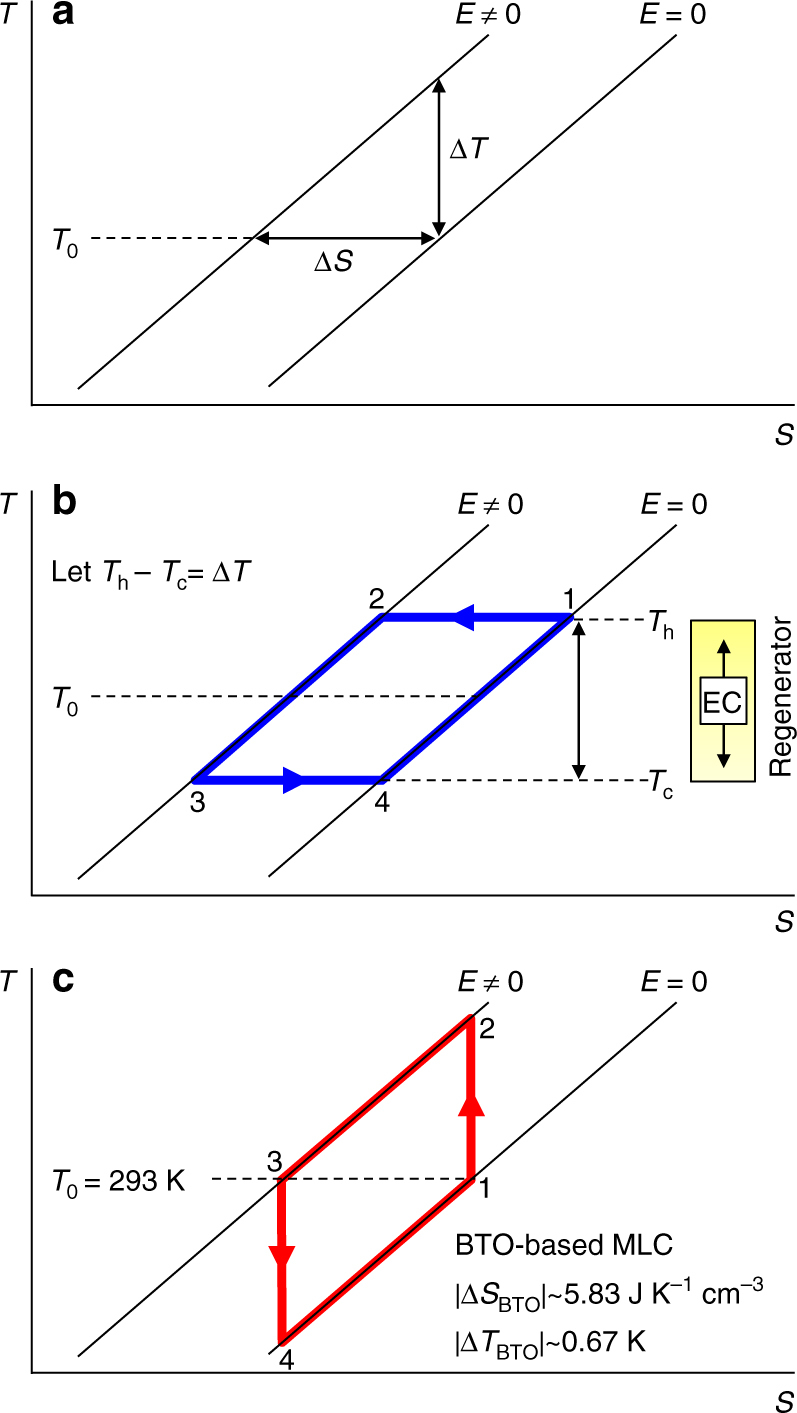
Simplified EC materials performance and resulting refrigeration cycles. a Near and at optimum starting temperature T₀, we assume that one can achieve the maximum adiabatic temperature change ΔT, and the maximum isothermal entropy change ΔS, due to a change of applied electric field E. For the performance schematised in a, we show b an Ericsson cycle (1→2→3→4) where a thermal gradient in a fluid regenerator permits the separation of T_c (at which heat is absorbed) and T_h (at which heat is expelled), and c the Brayton cycle (1→2→3→4) that we realize experimentally using two BTO-based MLCs, C1 and C2. Values for |ΔT_BTO| and |ΔS_BTO| describe the BTO layers alone