mTM-align: an algorithm for fast and accurate multiple protein structure alignment

Abstract

Motivation

As protein structure is more conserved than sequence during evolution, multiple structure alignment can be more informative than multiple sequence alignment, especially for distantly related proteins. With the rapid increase of the number of protein structures in the Protein Data Bank, it becomes urgent to develop efficient algorithms for multiple structure alignment.

Results

A new multiple structure alignment algorithm (mTM-align) was proposed, which is an extension of the highly efficient pairwise structure alignment program TM-align. The algorithm was benchmarked on four widely used datasets, HOMSTRAD, SABmark_sup, SABmark_twi and SISY-multiple, showing that mTM-align consistently outperforms other algorithms. In addition, the comparison with the manually curated alignments in the HOMSTRAD database shows that the automated alignments built by mTM-align are in general more accurate. Therefore, mTM-align may be used as a reliable complement to construct multiple structure alignments for real-world applications.

Availability and implementation

http://yanglab.nankai.edu.cn/mTM-align

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

As protein structure is more conserved than sequence during evolution, multiple structure alignment (MSTA) can be more informative than multiple sequence alignment (MSA), especially for distantly related proteins. Currently, there are >130 thousand structures in the Protein Data Bank (PDB), with weekly increase of about 200 new structures (Rose et al., 2017). These data make it urgent to develop efficient algorithms for MSTA.

A few algorithms have been developed for MSTA in the past years. They can be broadly divided into two categories. The first one is based on progressive merging of pairwise structure alignments (PSAs), such as STAMP (Russell and Barton, 1992), SSAP (Orengo and Taylor, 1996), CE-MC (Guda et al., 2004), POSA (Ye and Godzik, 2005), MAMMOTH-mult (Lupyan et al., 2005), MUSTANG (Konagurthu et al., 2006), CBA (Ebert and Brutlag, 2006), SALIGN (Madhusudhan et al., 2009), MISTRAL (Micheletti and Orland, 2009), MAPSCI (Ilinkin et al., 2010), msTALI (Shealy and Valafar, 2012) and mulPBA (Leonard et al., 2014). The second is based on iterative fragment alignment and assembly, such as MultiProt (Shatsky et al., 2004), Matt (Menke et al., 2008), Smolign (Sun et al., 2012) and 3DCOMB (Wang et al., 2011). The former relies on PSAs and inaccurate PSAs may degrade the quality of the MSTA. The latter is computationally expensive, when making all-against-all comparisons of fragments. Note that some MSTA algorithms take the flexibility of protein structures into consideration, such as POSA (Ye and Godzik, 2005), Matt (Menke et al., 2008) and Smolign (Sun et al., 2012).

In this study, we developed a new MSTA algorithm (mTM-align), which builds a MSTA progressively based on the PSAs generated by the highly efficient program TM-align (Zhang and Skolnick, 2005). The flexibility of protein structure is not considered here and shall be included in future work. The algorithm was benchmarked on four widely used datasets, HOMSTRAD, SABmark_sup, SABmark_twi and SISY-multiple, demonstrating significant advantage over other MSTA algorithms.

2 Materials and methods

2.1 Benchmark datasets

Four datasets were collected to benchmark the proposed method. The first one is from HOMSTRAD (Stebbings and Mizuguchi, 2004), which is a manually curated resource of structure-based alignments for homologous protein families (version of Nov 2015). There are 1031 families in the original database. After filtering out the families with <3 structures, we obtained 398 families, each containing 3–27 structures. The next two datasets are from SABmark (version 1.65) (Van Walle et al., 2005), a resource for alignments of sequences with very low to medium sequence similarity. There are two subsets in SABmark: superfamily and twilight zone. The superfamily subset (denoted by SABmark_sup) contains 425 groups of structures with pairwise sequence identity <50%. The twilight zone subset (denoted by SABmark_twi) contains 209 groups of structures with pairwise sequence identity <25%. Each group in these two datasets contains at most 25 structures. The last one is SISY-multiple (Berbalk et al., 2009), which originally consists of 106 groups. The number of structures in each group is between 3 and 119. Because some of the compared methods failed to generate MSTA for 20 groups (e.g. MAMMOTH-mult only works for groups with <30 structures), only the remaining 86 groups were kept. Note that mTM-align works for all groups and the results are provided for download for future studies. All the benchmark datasets and the mTM-align results are available at http://yanglab.nankai.edu.cn/mTM-align/benchmark.

2.2 Algorithm for pairwise structure alignment

The alignment of two protein structures is done by TM-align (Zhang and Skolnick, 2005), a highly efficient program for pairwise structure alignment. It is introduced briefly here for the sake of convenience. TM-align aims to find a PSA that maximizes TM-score, a length-independent scoring function for measuring the similarity of two structures (Zhang and Skolnick, 2004):

$$\text{TM}‐\text{score}=\max \frac{1}{L}\sum _{i=1}^{N_{ali}}\frac{1}{1+{\left(d_i/d_0\right)}^2} .$$ (1)

where d_i is the distance between the i-th pair of Cα atoms of the two structures; L is the length of the target protein (one of the input structures); N_ali is the number of aligned residue pairs; and d₀ is a scale factor defined by:

$$d_0=\{\begin{array}{l}1.24\times \sqrt[3]{L-15}-1.8, \text{if} L>21\\ 0.5, \text{otherwise}\end{array}$$ (2)

TM-score is in the range of 0 to 1 and a higher value of TM-score indicates more similar structures.

A heuristic algorithm is used to generate a PSA efficiently in TM-align. Five different initial alignments are quickly identified based on: gapless threading (IA1), secondary structure (IA2), IA1 refined by secondary structure (IA3), local structure superposition (IA4) and fragment-based gapless threading (IA5). Each initial alignment is refined iteratively by a heuristic algorithm, which works as follows. First, the two structures are superimposed by the TM-score rotation matrix based on their initial alignment. Second, the similarity score for each pair of residues in the two structures is calculated based on their pairwise distance of the Cα atoms. Third, the similarity scores are used to generate a new alignment by the Needleman-Wunsch dynamic programming (NWDP) (Needleman and Wunsch, 1970). This procedure is repeated until the TM-score of the alignment does not increase. Finally, the alignment with the highest TM-score is returned.

2.3 Algorithm for multiple structure alignment

The MSTA algorithm is based on TM-align, thus we name it as mTM-align. The idea of mTM-align is borrowed from the MSA algorithm CLUSTALW (Thompson et al., 1994). Figure 1 shows the overall architecture of mTM-align, using the HOMSTRAD family ‘Bacterial regulatory helix-turn-helix proteins, araC family, single structural repeat’. Given a set of protein structures, their MSTA is built with three steps, which are introduced below in details.

Fig. 1.

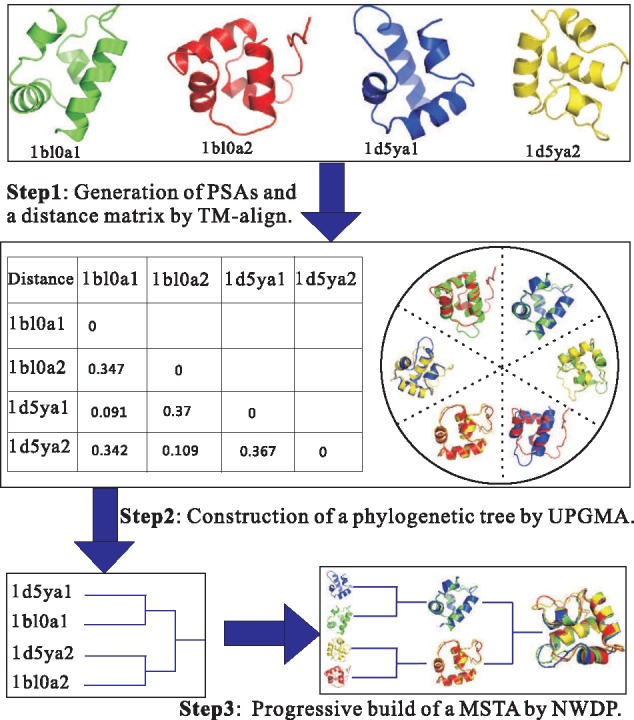
The architecture of mTM-align for progressive construction of a MSTA

2.3.1 Step 1. Generate the PSAs

Our algorithm starts by generating all the PSAs for the input structures with TM-align. Supposing the total number of the input structures is N, the number of possible structure pairs is then N(N − 1)/2. From TM-align, the PSAs and the associated TM-score for each pair of structures are obtained. In this study, the TM-score is normalized by the size of the smaller protein. When the sizes of two proteins differ significantly, the TM-score will be different considerably when normalized by the bigger one. This may impact the subsequent steps of mTM-align. Our tests reveal that this leads to about half of the families/groups with different phylogenetic trees. However, the TM-score of the common core (defined later) of the final MSTAs does not have a significant difference, reflecting that mTM-align is robust remarkably (please see Supplementary Table S1).

2.3.2 Step 2. Construct a structure-based phylogenetic tree

In order to guide the next step, a structure-based phylogenetic tree is constructed using the UPGMA algorithm (Sokal and Michener, 1958). The distance matrix used for the tree construction is calculated based on the TM-score from TM-align (i.e. 1-TM-score). A rooted tree is then constructed based on the distance matrix using the UPGMA algorithm.

2.3.3 Step 3. Build a MSTA progressively

The branching order from the phylogenetic tree is used to guide the progressive construction of a MSTA. Alignment of two structures is directly taken from TM-align. Aligning an already constructed alignment with another alignment/structure is performed using the NWDP algorithm.

There are two important factors in the procedure of NWDP. One is the scoring function for measuring the matching state. The other is the gap penalty (to be determined later). The score S(i, j) for matching the i-th column of the alignment A with the j-th column of the alignment B (or the j-th residue of a structure if B only contains one structure) is defined by the following equation.

$$S(i,j)=\sum _{m=1}^M\sum _{n=1}^{N}s(i_m,j_n)$$ (3)

where M (N) is the numbers of structures in the alignment A (B); i_m (j_n) is the index of the residue at the i-th (j-th) column for the m-th (n-th) structure; this index is null and the score s(i_m, j_n) is set to 0 if it is a gap insertion for the structure at this column; otherwise, it is calculated based on the PSA from TM-align below.

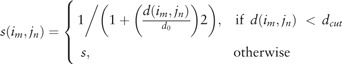(4)

where d(i_m, j_n) is the distance between the i_m-th residue in the m-th structure and the j_n-th residue in the n-th structure from PSA. Note that the calculation of d(i_m, j_n) is based on the TM-score rotation matrix in the first step and is unchanged in this step. d_cut is a distance cutoff introduced to punish matching distant residue pairs with a distance-dependent penalty:

$$s=\{\begin{array}{l}-0.1\times (1-e^{d_{cut}-d(i_m,j_n)}), \text{if} \overline{\text{TM}‐\text{score}}>0.5\\ -0.1\times (1-e^{d_{cut}-d(i_m,j_n)})/b(i_m,j_n), \text{otherwise}\end{array}$$ (5)

where b(i_m, j_n) is the corresponding value in the normalized BLOSUM62 matrix by 2^{0.1x BLOSUM62}, which has been used in previous work to convert the position-specific scoring matrix into a frequency matrix (Xia et al., 2017; Yang and Chen, 2011). The division by b(i_m, j_n) is inspired by the fact that both structure and sequence similarities have been considered in the HOMSTRAD database. Intuitively, the punishment is enlarged/shrunk for dissimilar/similar residues. This adjustment is only applied for the groups with low structural similarity (i.e. the mean pairwise TM-score is ≤ 0.5).

2.4 Metrics for performance evaluation

The quality of a MSTA is evaluated globally and locally. The PSAs deduced from a MSTA are called imposed pairwise alignments (IPAs).

The global metrics are defined based on the IPAs. For each IPA, four metrics are first defined. Two aligned residues are said to be structurally equivalent if they are within the distance of 4 Å after superimposition. We can calculate the number of structurally equivalent residues (L_ali), the associated Root-Mean-Square Deviation (RMSD) and TM-score. Here the TM-score is normalized by the length of the smaller protein. Because the reference MSTAs are available for the HOMSTRAD dataset, we can define another metrics accuracy (ACC). The reference MSTAs are also superimposed and the 4 Å cutoff is applied. The ACC of an IPA is defined as the number of structurally equivalent residue pairs consistent with the reference divided by the L_ali of the reference IPA. The global quality of a MSTA is then measured accordingly by averaging the values over all IPAs. For brevity, the same notations are also used.

The local metrics are defined for the common core regions. The common core of a MSTA is defined as the columns that do not contain any gap and all pairwise residue distances are smaller than 4 Å (Lupyan et al., 2005). To calculate the distances, the structures are superimposed to the same reference structure. Here, the reference structure is selected as the one with the longest non-gap alignment. The first local metric is the number of columns in the common core (L_core). The other two are the average pairwise RMSD (ccRMSD) and TM-score (ccTM-score), defined similarly as the average global RMSD and TM-score with the pairwise IPAs limited to the common core. The pairwise TM-score is also normalized by the length of the smaller protein. Note that because the length of a common core is usually smaller than the lengths of the individual proteins, the values of the ccTM-score are smaller than TM-score. However, it is still meaningful to compare different MSTA methods using the ccTM-score because it is normalized consistently for different methods.

It is worthwhile to mention that the alignment length L_ali (L_core) and RMSD (ccRMSD) are interdependent. Longer alignment tends to give higher RMSD (ccRMSD) values. Therefore, only comparing these values for different MSTA methods may be problematic. On the contrary, the TM-score (ccTM-score) is a length-independent metrics and is more suitable for comparing different methods objectively.

Finally, the running time (RT, in seconds) is used to compare the speed of different methods. The RT for a dataset is computed as the total amount of the time spent divided by the number of families/groups in the dataset.

3 Results and discussion

3.1 Parameter optimization

Two parameters remain to be determined: the gap penalty in NWDP and d_cut in Equations (4 and 5). A training set was constructed by randomly selecting 50% groups from the dataset SABmark_twi. To reduce the training time, the gap penalty was set to 0 when tuning d_cut. The gap penalty was optimized after d_cut was fixed. The ccTM-score was used for optimization. After the optimization, the values for d_cut and the gap penalty were 4 and 0.2, respectively (see Supplementary Fig. S1).

Note the ACC was not used for optimization based on the following observations. First, the ACC is only available for the HOMSTRAD dataset. This dataset might be too easy (as indicated by the high pairwise TM-score in Supplementary Table S1) to be sensitive to the parameter tuning. In fact, the ACCs for almost all the compared methods are above 0.9. Second, when optimizing for the ACC, a slightly higher accuracy could be obtained (0.946 versus 0.934). However except ccRMSD, the results for other metrics all became worse for all datasets (Supplementary Table S2).

3.2 Comparison with other MSTA methods

We compare mTM-align with five widely used MSTA programs: MUSTANG (Konagurthu et al., 2006), Matt (Menke et al., 2008), MultiProt (Shatsky et al., 2004), Promals3D (Pei et al., 2008) and MAMMOTH-mult (Lupyan et al., 2005). These programs were installed locally and ran with the default parameters. As MultiProt does not generate alignment of the full structures, the global metrics for this method are not applicable. The comparison results on the four benchmark datasets are listed in Tables 1–4.

Table 1.

The comparison of methods on the HOMSTRAD dataset

Metrics	M1	M2	M3	M4	M5	M6	Ref.
Lcore	146.6	139.4	135.6	130.2	117.2	138.6	134.1
ccRMSD	1.3	1.29	1.26	1.26	1.21	1.22	1.24
ccTM-score	0.674	0.641	0.618	0.602	0.546	0.642	0.619
Lali	173.8	167.8	166	162.7	154.3	NA	164.4
RMSD	1.46	1.48	1.48	1.49	1.50	NA	1.48
TM-score	0.784	0.758	0.746	0.735	0.7	NA	0.742
ACC	0.934	0.914	0.918	0.918	0.879	NA	1
RT	2.48	31.94	1.7	19.72	187.3	34.03	NA

Note: M1–M6 represents mTM-align, Matt, MAMMOTH-mult, MUSTANG, Promals3D and MultiProt, respectively. Ref. denotes the reference alignment given in the HOMSTRAD database. The best results are highlighted in bold type.

On the HOMSTRAD dataset, mTM-align achieves the highest L_core and ccTM-score of 146.6 and 0.674, respectively. The ccTM-score improvements by mTM-align over Matt, MAMMOTH-mult, MUSTANG, Promals3D and MultiProt are 5.1%, 9.1%, 12.0%, 23.4% and 5%, respectively. The ccRMSD of mTM-align is 1.3, slightly higher than other methods. This is because the common core returned by mTM-align is much larger than others (e.g. 146.6 versus 117.2 for Promals3D). The global TM-score by mTM-align are also higher than other methods (e.g. 0.784 versus 0.758 for Matt). Interestingly, the RMSD for mTM-align is lower than other methods though its alignment is the longest, suggesting that the longer alignments by mTM-align are indeed structurally more conserved than others. The ACC for mTM-align is 0.934, slightly higher than other methods as well. As shown by the RT, the speed of mTM-align is slightly slower than MAMMOTH-mult. However, this method has significantly lower ccTM-score than mTM-align (0.618 versus 0.674). Compared with the second best methods (in terms of ccTM-score), mTM-align is 12.9 and 13.7 times faster than Matt and MultiProt, respectively.

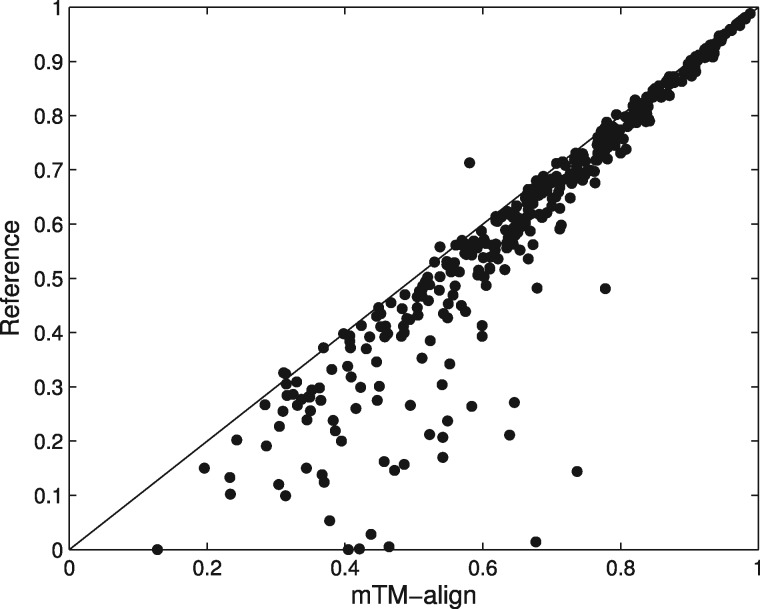
We also calculated the corresponding metrics for the reference MSTAs given in the HOMSTRAD dataset and the results are also listed in Table 1. We can see that except the ccRMSD, other metrics for mTM-align are all better than the reference. A head-to-head ccTM-score comparison between mTM-align and the reference is shown in Figure 2. mTM-align’s alignment has higher/lower ccTM-score for 362/12 families than the reference. For the remaining 24 families, the ccTM-scores for both are equal. Note that the reference MSTAs in HOMSTRAD were obtained with automated structure alignment followed by manual investigation. Replacing the automated alignment part by mTM-align should be beneficial for constructing more accurate MSTAs.

Fig. 2.

Comparison of the ccTM-score between the MSTAs generated by mTM-align and the reference MSTAs in the HOMSTRAD database

Figure 3 shows an example family (‘YgbB’) that mTM-align generates more reasonable alignment. There are three structures in this family. From the front view, compared with the reference (Fig. 3A), the four beta strands highlighted in magenta are aligned much better for mTM-align (Fig. 3C). After rotating by 180^° to the back view, we can see that the three alpha helices are also aligned very well for mTM-align (Fig. 3D). In contrast, the reference alignment is very divergent for these helices (Fig. 3B). These make the common core of mTM-align’s MSTA much bigger (124 versus 76) and thus has a higher ccTM-score than the reference MSTA (0.78 versus 0.49).

Fig. 3.

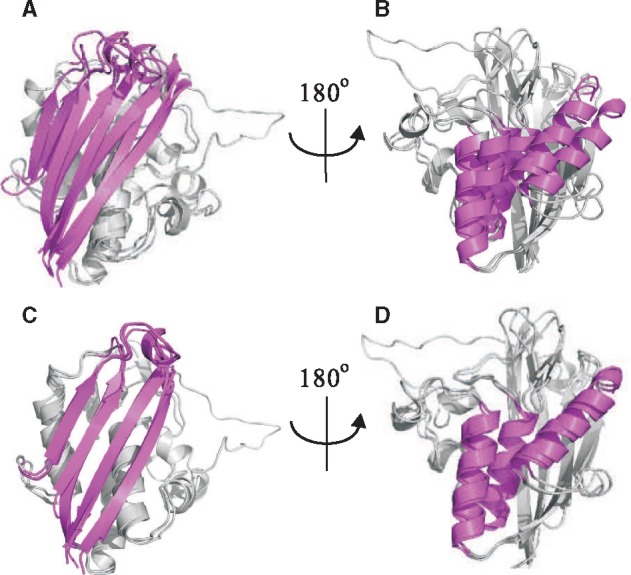
An example family (‘YgbB’) showing that mTM-align (C, D) has structurally more convergent MSTA than the reference given in HOMSTRAD (A, B)

Table 2 lists the results on the SABmark_sup dataset, which shows that the ccTM-score and TM-score for all methods are lower than the HOMSTRAD dataset, meaning that the structures in this dataset are less similar and more challenging to align. We can see that mTM-align outperforms other methods in terms of L_core, ccTM-score, L_ali and TM-score. For example, the ccTM-score for mTM-align is 0.426, which is 8.7%, 26.8%, 32.3%, 73.2% and 9% higher than Matt, MAMMOTH-mult, MUSTANG, Promals3D and MultiProt, respectively. The slightly higher ccRMSD by mTM-align can be explained by the common core with bigger size (72.9). For the global metrics, mTM-align achieves the highest TM-score (0.627) and L_ali (112.9) while maintaining similar RMSD with other methods. As shown by the RT, mTM-align takes 4.22 seconds per group, about 1.8 times of the method MAMMOTH-mult, which however does not perform well as indicated by the lower ccTM-score. The ones with relatively closer performance to mTM-align are Matt and MultiProt, which are about 11.9 and 16.3 times slower than mTM-align, respectively.

Table 2.

The comparison of methods on the SABmark_sup dataset

Metrics	M1	M2	M3	M4	M5	M6
Lcore	72.9	66.1	57.5	53.6	41	64.4
ccRMSD	1.43	1.37	1.13	1.15	0.9	1.34
ccTM-score	0.426	0.392	0.336	0.322	0.246	0.391
Lali	112.9	101.9	95.9	94.1	82.1	NA
RMSD	1.80	1.82	1.71	1.75	1.71	NA
TM-score	0.627	0.576	0.537	0.533	0.467	NA
RT	4.22	50.34	2.29	50.55	325.8	68.65

The dataset SABmark_twi is even more challenging to align than SABmark_sup, as shown by the low TM-score of all methods in Table 3 (<0.5). The ccTM-score of all methods are relatively lower because the contribution to this score is only from the common core but normalized by the full length of the structures. The common core for this dataset is relatively smaller as shown by the low ratio of L_core/L_ali (50%) for mTM-align. In comparison, the corresponding ratios for the HOMSTRAD and SABmark_sup datasets are 84% and 65%, respectively. mTM-align achieves ccTM-score (TM-score) of 0.273 (0.486), which is 8.3% (20%) higher than Matt. The ccRMSD of Promals3D is the lowest because it generates MSTAs of very small common core, indicated by the low value of L_core (12 compared with 38.1 for mTM-align). For the running time, mTM-align takes 4.2 s per group in this dataset, which is about 12.3 times faster than Matt.

Table 3.

The comparison of methods on the SABmark_twi dataset

Metrics	M1	M2	M3	M4	M5	M6
Lcore	38.1	34	23.2	21.3	12	31.8
ccRMSD	1.39	1.34	0.88	0.91	0.56	1.32
ccTM-score	0.273	0.252	0.171	0.168	0.1	0.24
Lali	76.1	60.8	51.9	52.7	38.3	NA
RMSD	2.04	1.94	1.73	1.89	1.75	NA
TM-score	0.486	0.405	0.344	0.356	0.264	NA
RT	4.2	51.79	2.03	60.78	391.1	71.15

Comparisons on the SISY-multiple dataset demonstrate that mTM-align outperforms other methods again. Table 4 shows that mTM-align generates the longest alignment (with L_ali of 135.5) and the biggest common core (with L_core of 80.5). Compared with Matt, the TM-score and ccTM-score of mTM-align are 10.7% and 7.4% higher, respectively, while with similar RMSD and ccRMSD. As to the running time, mTM-align takes 6.19 seconds per group, which is about 15 times faster than Matt and MultiProt, the two methods with the second highest ccTM-score.

Table 4.

The comparison of methods on the SISY-multiple dataset

Metrics	M1	M2	M3	M4	M5	M6
Lcore	80.5	75.2	59	53.1	38.9	76
ccRMSD	1.33	1.31	0.95	0.84	0.74	1.27
ccTM-score	0.422	0.393	0.289	0.271	0.197	0.39
Lali	135.5	116.6	108.6	106.2	94.3	NA
RMSD	1.74	1.75	1.58	1.57	1.54	NA
TM-score	0.629	0.568	0.505	0.494	0.432	NA
RT	6.19	90.98	3.23	69.73	240.5	90.19

3.3 Running time analysis for mTM-align

As mTM-align builds the MSTA based on the PSA generated by TM-align, we decompose the total running time into two parts, the PSA part by TM-align and the remaining used for building the MSTA (mainly by NWDP). The results are shown in Table 5. We can see that the major running time for mTM-align is in the PSA part. For example, TM-align takes about 85%, 75%, 75% and 80% of the total running time for the HOMSTRAD, SABmark_sup, SABmark_twi and SISY-multiple datasets, respectively. Note that the running time by mTM-align is dependent on two factors: the average number of the structure pairs to be aligned and the average length of the structures. Table 5 shows the average number of pairs in the HOMSTRAD dataset is about half of the other three datasets. Such a significant difference makes both the PSA and the NWDP parts take more time for these datasets than the HOMSTRAD dataset. In addition, though the numbers of structure pairs are similar (28) for the SABmark_sup and SISY-multiple, the structures in the latter are bigger (172.6 versus 228.8), making it takes more time for the latter (4.22 versus 6.19).

Table 5.

The running time for mTM-align

Dataset	#Pairs	Length	PSA	NWDP	Total
HOMSTRAD	15	205.5	2.12	0.36	2.48
SABmark_sup	28	172.6	3.16	1.06	4.22
SABmark_twi	36	153.4	3.15	1.05	4.2
SISY-multiple	28	228.8	4.98	1.21	6.19

3.4 Factors affecting the performance of mTM-align

As shown in Figure 1, mTM-align consists of three key steps for generating a MSTA: the PSA by TM-align, the phylogenetic tree construction by UPGMA, and the progressive build of a MSTA by NWDP. Thus we analyze the factors in these steps impacting the performance of mTM-align.

3.4.1 Impact of the PSA

The program TM-align with the default option has been used to generate the PSAs. It would be interesting to use other programs to produce alternative PSAs. We tried to output different PSAs from TM-align, representing different alignment methods. As there are five different initial alignments in TM-align, we tested five alternative PSAs that are obtained with only one of those initial alignments (IA1–IA5. Please refer to the Section 2.2). Supplementary Table S3 lists the average TM-score of different PSAs and the corresponding ccTM-score and TM-score of the MSTAs. We can see that for all datasets, the default PSA has the highest pairwise TM-score and the MSTA built based on it also has the highest ccTM-score and TM-score. Comparison between these alignments suggests that the PSA with a higher TM-score tends to produce a MSTA with better quality. Thus, a direct way to improve mTM-align in future is improving the first step of PSA.

3.4.2 Impact of the phylogenetic tree construction algorithm

The UPGMA algorithm has been used to construct the phylogenetic tree to guide the progressive merging of alignments. For comparison, we tried the neighbor-joining (NJ) method (Saitou and Nei, 1987) to construct the phylogenetic tree. As an extreme case, we skip the step of tree construction and merge the alignments randomly. The time used for phylogenetic tree construction is negligible and thus the running time is not compared here. Supplementary Table S4 shows that the utilization of phylogenetic tree does help build MSTA with higher ccTM-score and TM-score than the random method. Comparison between the UPGMA and NJ suggests that the former is consistently better for all datasets.

3.4.3 Impact of the scoring function in DP

In the scoring function [i.e. Equation (4)], matching distant residue pairs is discouraged by a penalty given by Equation (5). We tested its impact to mTM-align when not using any penalty. The ccTM-score and TM-score with both scoring functions are shown in Table 6. It suggests that using penalty consistently outperforms that without penalty for all datasets.

Table 6.

The impact of the scoring function to mTM-align

Dataset	With penalty		Without penalty
	ccTM-score	TM-score	ccTM-score	TM-score
HOMSTRAD	0.674	0.784	0.647	0.766
SABmark_sup	0.426	0.627	0.394	0.594
SABmark_twi	0.273	0.486	0.247	0.451
SISY-multiple	0.422	0.629	0.382	0.587

3.5 What went right?

As discussed in the last section, the MSTA built from more accurate PSAs has higher ccTM-score and TM-score. This means that when the PSAs are accurate, mTM-align is anticipated to build accurate MSTAs. The HOMSTRAD dataset is used to verify this hypothesis. We calculate the average accuracy (ACC) of TM-align’s PSA and the IPA from mTM-align’s MSTA. The correlation is shown in Supplementary Figure S2. The Pearson correlation coefficient (PCC) is 0.94, indicating that more/less accurate PSA results into MSTA of higher/lower accuracy.

It is worthwhile to mention that there are 95 groups above the diagonal line of Supplementary Figure S2, meaning that the MSTA by mTM-align has higher accuracy than the PSA by TM-align. This can be attributed to the progressive merging of alignments by NWDP, which helps fixing some wrong PSAs. For example, for the family ‘EF-TS’ (Fig. 4) that consists of three structures, the accuracy of the PSAs is 0.667, which increases to 0.947 in the MSTA. This improvement is due to the correction of the PSA between the structures shown in Figure 4A, which has accuracy of 0 and goes up to 1 after the correction. In addition, Figure 4B and C shows that in the zoomed regions, the mTM-align alignment is much more convergent than the HOMSTRAD alignment. As a result, the MSTA by mTM-align has significantly higher ccTM-score than the MSTA in HOMSTRAD (0.37 versus 0.124).

Fig. 4.

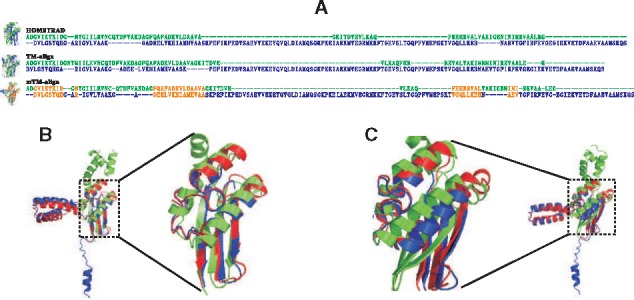
An example family (‘EF-TS’) showing that mTM-align corrects the PSA and generates a MSTA with higher ccTM-score than the reference alignment by HOMSTRAD. (A) The PSA by TM-align and the IPA for the chains 1efud1 (in green) and 1efud2 (in blue). The correct alignments compared with the reference are highlighted in orange. (B) and (C) are the MSTAs by mTM-align and HOMSTRAD, respectively

3.6 What went wrong?

From Figure 2, we can see there are a few families (12) for which mTM-align generates MSTAs with lower ccTM-score than the reference. We took a closer check at the one with the biggest difference, i.e. the family ‘hexapep’. There are three structures in this family. Compared with reference, the ACC for the PSA is very low (0.328). This is mainly because there is a shift of 31 residues in the PSA between the red structure and the other two shown in wheat cartoon in Figure 5. However, the pairwise TM-score of the alignment with the one in red trace is slightly higher (0.795 versus 0.741) than that in blue trace, which is understandable as TM-align aims to maximize the TM-score. The consideration of the sequence similarity in the scoring function [i.e. Equation (5)] was proposed to solve such issues. This does help improve the alignments for some families/groups. Unfortunately, it failed to correct the errors for this example. In addition, we tried to use multiple sub-optimal PSAs from TM-align to partially solve such issue. However, this strategy makes the algorithm complicated and significantly slows down the program and thus is not considered here. Better strategy may be explored in future work.

Fig. 5.

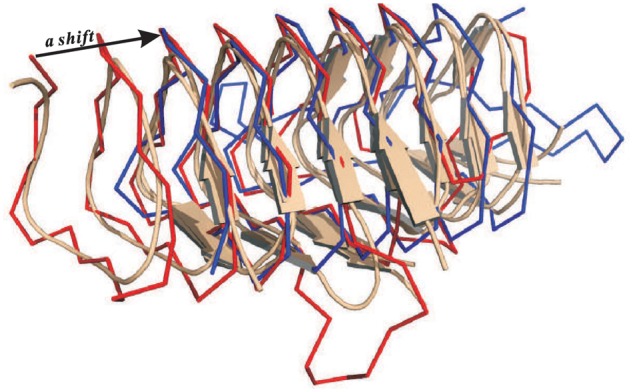
An example family (‘hexapep’) showing that mTM-align fails to generate an accurate MSTA due to the very low accuracy of the pairwise alignment, caused by a shift in the pairwise alignment. Following the branching order in the phylogenetic tree, the two structures (shown in wheat cartoon) were first aligned and the third structure (shown in red trace) was then added to the alignment. The structure in blue trace is from the reference alignment, which is basically a shift of the structure in red trace

4 Conclusions

A new algorithm mTM-align for multiple protein structure alignment has been developed, which is an extension of the highly efficient pairwise structure alignment program TM-align. The algorithm was benchmarked on four datasets, demonstrating that mTM-align outperforms many other MSTA algorithms, such as Matt, MUSTANG and MultiProt. In addition, comparison with the manually curated alignments in the HOMSTRAD database shows that the automated alignments built by mTM-align are in general more accurate. Therefore, mTM-align may be used as a reliable complement for constructing multiple structure alignment for real-world applications.

Funding

This work has been supported by the National Natural Science Foundation of China (NSF) [Grant No. 11501306, 11501407]; National Institutes of Health (GM083107 and GM116960), National Science Foundation (DBI1564756) and the Thousand Youth Talents Plan of China.

Conflict of Interest: none declared.