Slow-Down in Diffusion in Crowded Protein Solutions Correlates with Transient Cluster Formation

Abstract

For a long time the effect of crowded cellular environment on protein dynamics has been largely ignored. Recent experiments indicate that proteins diffuse much slower in a living cell than in a diluted solution and further studies suggest that the diffusion depends on the local surrounding. Here, detailed insight into how diffusion depends on protein-protein contacts is presented based on extensive all-atom molecular dynamics simulations of concentrated villin head piece solutions. After force field adjustments in the form of increased protein-water interactions to reproduce experimental data, translational and rotational diffusion was analyzed in detail. While internal protein dynamics remained largely unaltered, rotational diffusion was found to slow down more significantly than translational diffusion as the protein concentration increased. The decrease in diffusion is interpreted in terms of a transient formation of protein clusters. These clusters persist on sub-microsecond time scales and follow distributions that increasingly shift toward larger cluster size with increasing protein concentrations. Weighting diffusion coefficients estimated for different clusters extracted from the simulations with the distribution of clusters largely reproduces the overall observed diffusion rates, suggesting that transient cluster formation is a primary cause for a slow-down in diffusion upon crowding with other proteins.

TOC image

INTRODUCTION

The cellular environment is very crowded. Up to 40% of the cell volume, i.e. as much as 400 mg/ml, is occupied by macromolecules such as proteins, lipids, and nucleic acids.¹ More than half of this fraction are proteins² that draw particular attention because of their functional relevance. For a long time, the importance of the cellular surrounding has not been fully appreciated as most of the experimental and theoretical studies were restricted either to the analysis of proteins in dilute solution or to simplifying considerations of cellular crowding effects.³ Since recently, an increasing number of studies of proteins in realistic cellular environments^4–6 indicate that in vivo conditions can have a substantial impact on protein structure and dynamics,^7–9 with crucial consequences for their biological function.¹⁰

One of the most important properties in the context of cellular environments is protein diffusion as a key determinant of biological processes.^11–14 Studies conducted in vivo indicate that both translational and rotational motions of proteins are significantly slower in vivo than in dilute solution.^15–18 However, the degree of retardation varies significantly, even within the same cell depending on the subcellular environment.¹⁹ Reduced diffusion may slow down reactions or speed up others, e.g. by extending the presence of a ligand in the vicinity of a receptor.²⁰ The best-understood effect of crowded cellular environments is the so-called excluded-volume effect where crowder molecules limit the available volume for a given solute.²¹ When the volume fraction of crowder molecules increases, diffusion is reduced simply because the free space is diminished, but there are additional factors beyond the excluded-volume effect that affect protein diffusion in a cell.²² Altered solvent properties such as higher viscosity and a reduced dynamics of water²³ could influence macromolecular diffusion, although some experiments indicate that the intracellular viscosity is not a limiting factor for protein tumbling in cells.^{24, 25} Finally, weak non-specific transient interactions with cytoplasmic components, often termed quinary interactions^{26, 27}, have recently been considered as key factors governing protein diffusion.^{8, 15, 16, 28} However, the nature and time scales of how such interactions may shape diffusive properties remains unclear.

It has been shown previously, mostly for lysozyme protein solutions,^29–31 that even at moderate concentrations proteins are prone to form dynamic clusters. As the protein concentration increases, solutions initially dominated by single proteins have been seen to develop large, branched and irregular clusters³² that persist on a finite time even above the geometric percolation threshold.³⁰ Other recent studies indicate that, although dynamic, such clusters persist long enough to retard the overall protein diffusion,³¹ as diffusion is simply size-dependent.³³ The general expectation has been that the cluster formation primarily affects short-time diffusion, whereas long-time diffusion is believed to be still determined by individual proteins which would be reflected in time-scale dependent diffusive behavior. Such behavior would be consistent with colloidal suspensions, where cluster formation has been seen as a result of weak short-range attraction and long-range repulsion.³⁴ For both, protein solutions and colloids in general, it has been shown that shifting the balance toward more attractive interactions, e.g. increasing the concentration, decreasing temperature, or screening the repulsive electrostatic by high ionic strength or pH, enhances cluster formation and the possibility of liquid-liquid phase separations.^{29, 30, 33–37} Studies of colloids, furthermore, show that as clusters grow, a transition to glass and gel phases occurs where dynamically arrested states are formed before crystallization occurs.³⁸ Experiments, theory and simulations of colloid systems generally assume that besides the attraction-dominated states, where particles move together, a repulsion-dominated state exists, where particles are trapped in a cage formed by surrounding particles.³⁹ All of these effects might be expected to contribute to the protein diffusion in a dense solution. Nevertheless, it is questionable to what extend the dynamics of a protein solution might be explained in terms of simple colloidal chemistry since the interactions between proteins are highly complex^{40, 41} and the present study aims to shed more light on such questions.

Experimental studies of protein dynamics under in vivo conditions or even in the presence of high concentrations of biological crowders such as other proteins are possible but do not always provide full detailed mechanistic insights.^42–44 Molecular dynamics (MD) simulations are available as an alternative to study crowded systems in atomistic detail. Recent MD simulations have investigated the properties of water^{23, 45}, the stability of proteins^{8, 9}, the conformational sampling of peptides⁴⁶, and interactions between proteins²⁸ under crowding conditions. A more extensive review is available elsewhere.⁶

In this study, we describe MD simulations of the well-studied globular protein villin headpiece (simply referred to as ‘villin’ throughout this manuscript) at a range of concentrations from dilute conditions to 10% volume fraction, close to the experimental solubility limit for villin.⁹ Since villin is not expected to aggregate or form specific clusters, it is used here as a model system for studying the effect of cellular crowding on macromolecular diffusion. Previous studies have indicated that current force fields may lead to artificial protein aggregation under self-crowding conditions^{47, 48}, including for villin.⁴⁸ A similar observation was also made for the sampling of disordered peptides that form ensembles that are generally too compact with most force fields.^{49, 50} Both findings suggest that protein-water interactions may be too weak relative to protein-protein interactions. To restore the balance, modified force fields enhance the Lennard-Jones potential between water and protein atoms.^{49, 51} We followed the same strategy here and initially calibrated a modified force field with scaled water-protein interactions to match solution properties of villin known from experiment. The trajectories with the optimal force field were then further analyzed with respect to diffusive properties and their dependence on transient cluster formation under crowding conditions.

METHODS

Crowded Protein Systems

The chicken villin headpiece HP-36 (PDB entry 1VII⁵²) was simulated at concentrations of 8, 16, and 32 mM. Systems at 8 and 16 mM concentrations consisted of eight villin copies. Systems at 32 mM had either eight or 64 copies of villin (see Table 1). In the initial configuration of each system, the proteins were placed in a cubic box in non-overlapping random positions and orientations (see Fig. 1). The box sizes were chosen to achieve the desired concentrations (see Table 1) and to be significantly larger than the characteristic molecular scales. The box edges are long enough to accommodate 5–10 villin molecules if packed together and are several times larger than average inter-protein distances. Periodic boundary conditions (PBC) were applied to avoid boundary effects. The systems were then solvated with TIP3P water and random water molecules were substituted with two Cl⁻ ions per villin molecule to neutralize each system. A system consisting of one copy of villin was used as a reference for infinite dilution. The size of the dilute system was chosen to prevent the protein from interacting with its own images under PBC, even when partially unfolded, neither directly nor indirectly (via mediated water layers). Throughout the manuscript we use residue numbering 1–36 for the villin residues that correspond to residues 41–76 in the full biological sequence.

Table 1.

Simulated concentrated villin solutions

[villin]		Np1	V (%)2	#atoms3	Box length4 (nm)
(mM)	(g/L)
dilute	–	1	–	21 K	5.9
8	34	8	2.5	165 K	11.8
16	77	8	5.0	74 K	9.0
32	138	8	10.0	41 K	7.5
32	135	64	10.0	336 K	14.9

¹number of protein copies;

²volume fraction occupied by the proteins;

³total number of atoms including ions and water molecules;

⁴after equilibration in the NPT ensemble.

Figure 1.

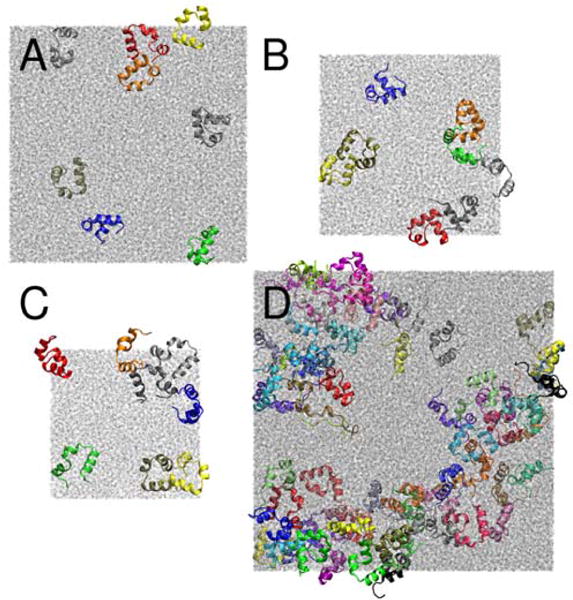
Configurations after 100 ns for concentrated systems of eight villins at 8 mM (A), 16 mM (B), and 32 mM (C) as well as 64 villins at 32 mM (D) concentration. Colors are used to distinguish different villin copies, water molecules are shown in grey.

Molecular Dynamics Simulations

All-atom MD simulations were carried out with NAMD⁵³ (version 2.10), CHARMM⁵⁴ (version 42a1) together with OpenMM⁵⁵, and GENESIS⁵⁶. The initial systems were subjected to energy minimization, heated to 298 K and then simulated for 2 μs. The CHARMM c36 force field⁵⁷ was used to describe interactions involving villin and ions and TIP3P⁵⁸ was used as the water model. Protein-water interactions were enhanced following the prescription by Best et al.⁴⁹. Using NBFIX, scaling factors λ between 1.00 and 1.10 in a modified Lennard-Jones potential were applied to interactions between water atoms i and protein atoms j:

$$V_{LJ}(r_{ij})=\lambda {\epsilon }_{ij}\left\{{\left(\frac{R_{ij}^{\mathit{min}}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{ij}^{\mathit{min}}}{r_{ij}}\right)}^6\right\}$$ (1)

The Lennard-Jones and short-range electrostatic interactions were shifted to zero at 0.9 nm in the one- and eight-villin systems and were cut off at 0.9 nm with a switching function becoming effective at 0.8 nm in the 64-villin system. Long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) summation method⁵⁹ under PBC. A more extensive description of the MD protocol can be found in the Molecular Dynamics Simulations section of the SI.

Folding Free Energy via Replica Exchange Simulations

Simulations of the one-copy villin were performed with Hamiltonian Replica Exchange MD (H-REMD) using λ values of 1.05, and 1.10 to obtain folding free energies, ΔGf, of villin. Unfolded protein conformations were generated by biasing the distance between C_α of Arg15 (in the second α-helix) and C_α of Leu29 (in the third α-helix) to facilitate the folding-unfolding transition as introduced in a previous study⁶⁰. 20 replicas were run where a harmonic potential using a force constant of k=4.5 kcal/mol was varied to target distances ranging from 1.05 to 2.19 nm with a spacing of 0.06 nm between replicas. Each replica was simulated over 100 ns with exchange attempts every 10 ps.

The potential of mean force (PMF) as a function of distance (d) and root-mean-square deviation (RMSD) was calculated using 2D Weighted Histogram Analysis Method (WHAM) implemented by Alan Grossfield.⁶¹ The 2D PMF was further integrated to obtain 1D PMFs as a function of RMSD. The ΔGf was calculated as a probability ratio of finding the protein in unfolded (UF) and folded (F) states, according to:

$$\mathrm{\Delta }{G}_f=-k_{B}T\ln K=-k_{B}T\ln \left[\frac{{\displaystyle {\sum }_{i\in F}p(\mathit{RMS}{D}_i)}}{{\displaystyle {\sum }_{i\in UF}p(\mathit{RMS}{D}_i)}}\right]$$ (2)

where k_B is Boltzmann constant, T is temperature, and K is the equilibrium constant. The folded state was defined as RMSD<0.4 nm, whereas, the unfolded as RMSD>8.0 nm for λ=1.05, and RMSD>7.8 nm for λ=1.10. Averages and errors were calculated from 10-ns non-overlapping intervals. This protocol follows the analysis applied in Huang et al.⁶⁰ for the same system with λ=1.00, the results of which are used here as well for comparison.

Analysis

The analysis of the MD trajectories was performed with the MMTSB Tool Set⁶² and the VMD visualization package⁶³. Custom scripts were written for calculation of translational diffusion, contacts between proteins, time scales of contacts formation, and distribution of clusters. The SciPy package⁶⁴ was applied for fitting data. The Matplotlib⁶⁵ library was used for plotting the results.

The first 200 ns of each multiple protein copy trajectory were omitted from analysis to allow for full equilibration and avoid dependence on the initial configurations. Except for the calculation of order parameters (S²_l), only the snapshots of Cα positions saved every 100 ps were used.

Translational diffusion coefficients, D_t, were obtained from mean square displacements (MSD) of protein centers of mass for a given protein:

$$\mathit{MSD}(\tau )=\langle {(\overrightarrow{r}(t+\tau )-\overrightarrow{r}(t))}^2\rangle$$ (3)

where r is the position of the protein at time t, and τ is the lag time between the two positions. The MSD values were obtained by sliding an observation window of size τ from 0.1 ns to 100 ns along the trajectory in steps of Δt=0.1 ns. Dt was then calculated from the slope of a linear fit to MSD(τ) according to the Einstein relation:

$$D_t=\frac{\mathit{MSD}(\tau )}{6\tau }$$ (4)

D_t was further corrected for PBC artifacts taking account of altered water viscosity in the crowded systems (see Eq. S1 and S2 in the Analysis section in the SI).

The internal dynamic correlation function was calculated from the MD trajectories according to:

$$C_I(t)=\langle P_2\left|\widehat{\mu }(0)\cdot \widehat{\mu }(t)\right|\rangle$$ (5)

where P₂(x) is the second-order Legendre polynomial, μ describes the orientation of the unit N-H bond vector with respect to the molecular reference frame. The resulting functions were fitted with:

$$C_1(t)=S_l^2+(1-S_l^2){\mathrm{e}}^{-\frac{\mathrm{t}}{{\tau }_{\mathrm{e}}}}$$ (6)

where S²_l is the generalized order parameter that describes protein dynamics, and τ_e is the time constant for internal motions.

The rotational correlation function was determined from the trajectories following the protocol proposed by Wong and Case⁶⁶. Randomly distributed unit vectors were centered and rotated along with the protein before fitting it to a reference structure for each frame. Correlation functions were then obtained as:

$$C_O(t_i,t)={\langle P_2(n_j(t_i+t)\cdot n_j(t_i))\rangle }_j$$ (7)

where n_j(t_i) is one of the randomly distributed unit vectors (generated at time t_i). The correlation functions were then fitted to a double-exponential function:

$$C_O(t)=S_R^2{e}^{-\frac{t}{{\tau }_{Rs}}}+(1-S_R^2)e^{-\frac{t}{{\tau }_{Rf}}}$$ (8)

with fast, τ_Rf, and slow, τ_Rs, correlation times, and weighted by S_R². Rotational diffusion estimates were then obtained according to Eq. 9 and do not require a PBC correction.⁶⁷

$$D_r=\frac{1}{l(l+1)\tau }$$ (9)

where l=2 and the overall rotational correlation time τ is obtained from the fast and slow correlation times as follows:

$$\tau =S_R^2{\tau }_{Rs}+(1-S_R^2){\tau }_{Rf}$$ (10)

Additionally, averages of the inverse tumbling times were also calculated as they are more relevant for comparison with many experiments such as dynamic light scattering⁶⁸:

$${\tau }_{\mathit{ini}}{\left(\frac{S_R^2}{{\tau }_{Rs}}+\frac{1-S_R^2}{{\tau }_{Rf}}\right)}^{-1}$$ (11)

The correlation functions obtained at the highest concentrations were additionally fitted to a triple-exponential function since a double-exponential fit did not fully describe the data:

$$C_O(t)=S_{Rs}^2{e}^{-\frac{t}{{\tau }_{Rs}}}+S_{Rm}^2{e}^{-\frac{t}{{\tau }_{Rm}}}+(1-S_{Rs}^2-S_{Rm}^2)e^{-\frac{t}{{\tau }_{Rf}}}$$ (12)

where τ_Rf, τ_Rm, and τ_Rs are fast, medium and slow correlation times with the corresponding S_Rm² and S_Rs² weights.

For both, translational and rotational diffusion rates, errors were obtained from averaging over four subsequent 500 ns trajectory blocks in dilute and over the proteins copies in dense systems. To analyze transient cluster formation, two proteins were assumed to be in a contact if any of their Cα atoms were closer than 0.7 nm. Clusters were counted based on proteins in contact considering minimum images under PBC.

A residue contact map for interactions between proteins based on Cα coordinates was calculated as follows: For each residue i in a given protein copy, P_m, the minimum distance to residues j in other protein copies P_n, excluding m, was calculated as $d_{\mathit{min}}\left(r_{i(i\in P_m)},r_{j(j\in P_n)}\right)$. The distance for a given pair was then averaged by taking each protein m in turn as the starting point and by averaging over simulation snapshots. The example of a minimum distance calculation shown in Fig. S1 indicates that the resulting contact map is not strictly symmetric. The kinetics of contact formation was described by a correlation function depicting whether a contact is still present after a given period of time (see Eq. S3 in the Analysis section in SI). The correlation function was then fitted to a triple-exponential function:

$$C_c(t)=S_c^s{e}^{-\frac{t}{{\tau }_c^s}}+S_c^m{e}^{-\frac{t}{{\tau }_c^m}}+(1-S_s^c-S_c^m)e^{-\frac{t}{{\tau }_c^l}}$$ (13)

with short $({\tau }_c^s)$, medium $({\tau }_c^m)$, and long $({\tau }_c^l)$ relaxation times and weights ${S_c^s}_s$, $S_c^m$ and $S_c^l=1-S_c^s-S_c^m$. No constraints were applied when fitting Eq. 13 and the functional form implies a decay to zero at long times since we did not observe permanent contact formation as in aggregation.

Representative structures of clusters were extracted from the trajectories at the middle of a time interval when a cluster was formed for at least 1 ns. Uncertainties in the cluster distribution and in the diffusion of MD-derived structures were obtained by averaging over four subsequent 450 ns trajectory blocks (discarding 200 ns as equilibration).

Coarse-Grained Simulations

Coarse-grained simulations of purely attractive, neutral, and repulsive proteins were carried out for comparison. Systems of eight protein copies at 8, 16 and 32 mM concentrations were modeled and each of them was simulated with the three different types of interactions. For more details see the Coarse-Grained Simulations section in the SI.

RESULTS AND DISCUSSION

Force Field Optimization

Previous studies have indicated that current force fields may overestimate protein-protein interactions relative to protein-water interactions.^{47, 48} Therefore, we considered a modified force field based on CHARMM c36⁵⁷ where the Lennard-Jones potential between water oxygen and protein atoms was scaled by a factor λ (see Eq. 1) as proposed by Best et al.⁴⁹ We tested λ values between 1.0, corresponding to the unmodified force field, and 1.2, corresponding to protein-water interactions that are increased by 20%. Simulations with different scaling factors were carried out for the eight-copy villin systems at different concentrations (see Table 1) to determine which value of λ provides results that are most consistent with experiment.

Since the strength of the protein-water interactions modulates the hydrophobic effect, we first analyzed whether the stability of villin is maintained when protein-water interactions are enhanced. We found that λ values up to 1.09 do not significantly compromise the stability of the native state (with average RMSD values generally below 0.3 nm, see Fig. S2) while larger scaling factors led to significant destabilization of the native fold. With scaling factors of λ=1.09 and less, there was only occasional partial unfolding that lasted at most for tens of nanoseconds before refolding. With λ=1.10, we find more pronounced native state destabilization in the concentrated solutions, especially at 8 and 32 mM, but not under dilute conditions, based on the average RMSD values. We also calculated average internal order parameters S_l² (according to Eq. 6, see Table S2) and found little change up to scaling factors of 1.09 but a significant increase in internal dynamics with λ=1.10. Partial destabilization of villin in simulations under crowding conditions has been noted previously,⁹ although, in that case, the observed partial unfolding of villin was related to interactions with protein G that are not present here. Previous NMR experiments clearly showed that villin maintains its stability even at 32 mM, as there were only minor changes in chemical shifts for residues at the surface.⁹ Therefore, based on the stability analysis, we concluded that protein-water scaling factors of 1.10 or larger are not consistent with the NMR experiments.

We further analyzed the formation of clusters based on the contact definition described in the Methods section. Generally, as expected, small clusters (monomers, dimers etc.) dominated at low concentrations, whereas larger clusters appeared increasingly at higher concentrations (see Fig. S3). Also as expected, increasing scaling factors shifted the cluster distributions within a given concentration toward smaller clusters (see Fig. S3). The systems are too small and sampling requirements are too large to directly determine solubility from these simulations.⁶⁹ However, the fraction of the largest possible cluster (octamer) is an indicator of aggregation propensities and whether the solubility limit is approached or exceeded. At 8 mM, octamers were not formed to a significant extent with any scaling factors (see Fig. S3) indicating that villin remained fully soluble in all cases. Scaling factors of 1.00, 1.01, and 1.02 led to significant octamer populations at 16 mM (about 50%. see Fig. S3) while at 32 mM, scaling factors from 1.00 to 1.05 resulted in 50–100 % octamer formation. In experiments, villin is still soluble at 32 mM.⁹ This observation is not compatible with the strong aggregation found in the simulations at 16 and 32 mM with scaling factors below 1.03 and probably also not with larger scaling factors up to 1.05 where significant aggregation into large clusters is seen at 32 mM.

Since protein stability appears to be sensitive to the scaling factor in the studied range, as the RMSD results show, we calculated the folding free energy of a single villin using different λ values. PMFs as a function of RMSD are shown in Fig. S4. According to the analysis described in the Method section we determined ΔGf as −4.94 kcal/mol, −4.14 kcal/mol and −3.47 kcal/mol for λ equal to 1.00, 1.05, and 1.10, respectively. The comparison with experimental values of −2.4 kcal/mol⁷⁰ and −3.1 kcal/mol⁷¹ (for villin without the N-terminal methionine) suggests that the largest scaling factor gives the best agreement.

Taking all of the evidence together, it is clear that the scaling of protein-water interactions improves the agreement between simulations and experiment. On one hand, scaling factors above 1.05 are needed to prevent strong aggregation while factors of 1.10 and larger lead to native state destabilization in the presence of other villin molecules. The calculated folding free energies for a single villin in dilute conditions furthermore suggest that scaling factors closer to 1.10 are best. Therefore, λ=1.09 was chosen as the optimal scaling factor to describe the concentrated villin solutions studied here as the largest value that does not lead to significant destabilization under crowded conditions. Incidentally, this value is very close to the value of λ=1.10 chosen by Best et al. for the AMBER force field to improve the sampling of disordered peptides and protein-protein affinities⁴⁹, although it will require further studies to determine whether this exact scaling factor is generally optimal for simulating concentrated protein systems with the CHARMM force field.

The simulations at 8, 16, and 32 mM with λ=1.09 as well as an additional simulation of 64 villin copies at 32 mM, also with λ=1.09, were subsequently analyzed in more detail.

Internal Dynamics of Villin

The villin structures remained largely stable at all concentrations in the simulations. The average Cα RMSD values with respect to the NMR structure (PDB code: 1VII) were 0.26 ± 0.009 nm at 8 mM, 0.26 ± 0.007 nm at 16 mM, and 0.25 ± 0.005 nm and 0.31 ± 0.03 nm in the eight- and 64-villin systems at 32 mM. In the eight-villin simulations, two proteins spontaneously unfolded (8 mM and 16 mM concentrations) for tens of nanoseconds forming a structure of an open hairpin that mostly preserved the secondary structure before refolding. Four proteins unfolded in the 64-copy system partially losing the secondary structure and remaining extended for a longer time period. Native-state destabilization of villin upon crowding has been seen by us before in shorter simulations under different conditions,⁹ but the unfolding seen here is likely due to a much larger amount of sampling. Villin is only stable by 3.1 kcal/mol and folding/unfolding rates are on the order of 5 μs.⁷¹ Therefore it would be expected that villin can spontaneously unfold during microsecond-scale simulations even under dilute conditions.

The internal dynamics was further analyzed by calculating generalized order parameters Sl2 as a function of residue (see Fig. 2). The results suggest that there is little overall effect of crowding on the internal dynamics as a function of concentration, but it appears that villin flexibility may be slightly increased for residues 11–14 and 33–35 while being decreased for residues 4–9.

Figure 2.

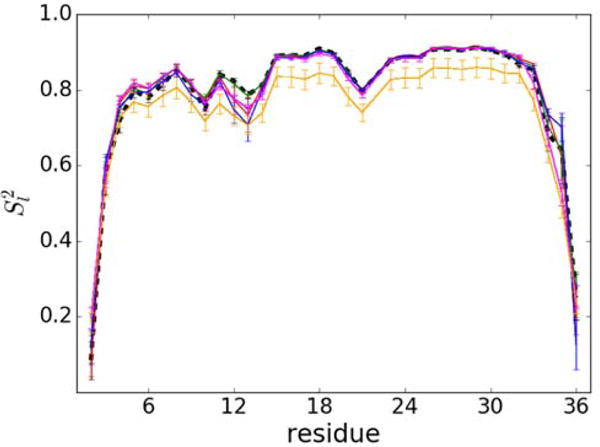
Order parameter S_l² for villin residues (except for Met1 and Pro22) at 8 mM (blue), 16 mM (green) and 32 mM (red: eight-villin system; orange: 64-villin system; magenta: 64-villin system without the four villins that unfold during the simulation). Results under dilute conditions are shown for reference as a black dashed line. Statistical uncertainties are shown as error bars.

Translational Diffusion of Villin

Translational diffusion coefficients were obtained from mean square displacements (see Fig. 3) and were corrected for PBC artifacts as described in the Methods section. The MSD curves display somewhat different slopes at different time scales indicative of transient behavior. Therefore, we obtained diffusion coefficients for three time regimes: < 1 ns, 1–10 ns, and 10–100 ns. Table 2 summarizes the results.

Figure 3.

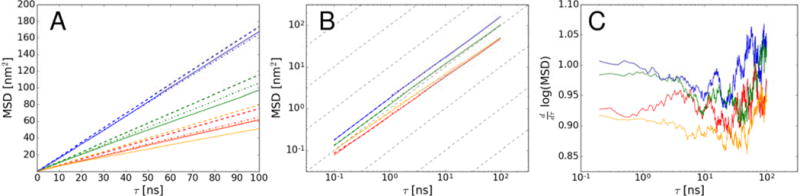
Mean square displacement vs. time based on center of mass of villin at 8 mM (blue), 16 mM (green), and 32 mM (eight-copy: red; 64-copy: orange). Linear functions fitted to different time scales (<1 ns, 1–10 ns, and 10–100 ns) are shown as dashed lines (dotted, dash-dotted, dashed, respectively). The values are shown in regular (A), logarithmic (B) scales. The derivative of the log-log plot is shown in (C). Gray dashed lines with the slop equal to 1 are shown for reference.

Table 2.

Translational diffusion coefficients of villin at different concentrations

[villin] (mM)	Np	Dt ;< 1 ns (nm2/ns; slow-down)		Dt ; 1–10 ns (nm2/ns; slow-down)		Dt ;10–100 ns (nm2/ns, slow-down)
dilute	1	0.49 (0.004)	1	0.48 (0.008)	1	0.46 (0.03)	1
8	8	0.43 (0.01)	0.88	0.41 (0.01)	0.85	0.40 (0.02)	0.87
16	8	0.35 (0.007)	0.71	0.34 (0.006)	0.71	0.31 (0.01)	0.67
32	8	0.25 (0.008)	0.51	0.24 (0.009)	0.50	0.22 (0.01)	0.48
32	64	0.21 (0.004)	0.43	0.18 (0.004)	0.38	0.16 (0.004)	0.35

Error estimates from averaging over blocks (dilute solution) and protein copies (concentrated solution) are given in parentheses. For each value, the slow-down relative to diffusion in dilute solvent is given in bold.

The TIP3P water model underestimates the viscosity of pure water (η_TIP3P = 0.35 cP⁷² (at 293 K) compared to the experimental value of η_exp = 0.89 cP⁷³). Therefore, the diffusion of solutes in TIP3P is too fast and a scaling factor based on the ratio of the viscosities, η_exp/η_TIP3P = 2.54 (at 298 K), has previously been applied to correct diffusion coefficients obtained with TIP3P water.⁷⁴ Based on this scaling factor, we obtain D_t = 0.187 nm²/ns under dilute conditions. Experimental data for D_t is not available for villin, but the program HYDROPRO provides theoretical estimates that generally match experimental values closely for dilute conditions.⁷⁵ The HYDROPRO estimate is D_t = 0.177 nm²/ns, in excellent agreement with the MD-derived value after scaling.

Under crowded conditions, diffusion rates slow down as expected. Diffusion on different time scales decreases to a different extent but the effect is not very strong (see Table 2 and Figure 3). Time-dependent diffusion in the presence of protein crowders has been examined before for CI2²⁸ and discussed in the context of variable protein-protein interactions. Standard colloid theory based on hard sphere models predicts two main diffusive regimes associated with faster short time diffusion within the cage of surrounding proteins and longer time diffusion where a molecule escapes the cage and is then affected by macroscopic solvent viscosity. In the case of CI2, this classical two-regime picture was seen in the case of weaker interactions with protein crowders, but when strong interactions with the surrounding protein crowders were present, the overall diffusion was reduced more and the cage effect was less pronounced as short and long time diffusion were similar.²⁸ The argument made in this earlier work was that diffusion was slowed down already at short time scales due to cluster formation while diminishing the cage effect. The absence of a strong cage effect is apparent from the log-log plot in Fig. 3B and the derivative analysis in Fig. 3C that shows slopes near 1 throughout the entire range of time scales with only a shallow minimum between 10–100 ns where the slope of the log-log curves decreases to 0.85–0.9 in the most concentrated system. This indicates only weak subdiffusive behavior for this system. The observation of similar short and long time diffusion in the villin simulations reported here then also suggests extensive cluster formation.

Similar results for the 8- and 64-copy systems at 32mM indicate that different box sizes do not have a strong effect on the findings reported here. On the other hand, the slightly more reduced diffusion rate in the 64-copy 32mM system can be rationalized simply because larger clusters can be formed than in the eight-copy system.

The simulations reported here are about an order of magnitude longer than our previous simulations of CI2 and the size of the villin molecules is smaller than then crowders in the CI2 study. More formally, the limits of short time diffusion are generally considered as τ_H ≪ t ≪ τ_I, with

$${\tau }_H\approx \frac{R^2\rho }{\eta \phi }\text{and}{\tau }_I\approx \frac{R^2}{D_{t,\mathit{dilute}}}$$ (12)

where R is the particle radius, ρ is the solvent density, η is the solvent viscosity, and ϕ is the volume fraction.⁴¹ For the 32 mM villin solution, this amounts to a time range of 25 ps ≪ t ≪ 11 ns, which is well below the 2-μs simulation length of the present simulations. Therefore, villins would have enough time to diffuse out of a local cage environment and reach the long-time diffusion limit. Further evidence that this is indeed the case comes from analyzing the exchange of the nine closest partners, N_ex⁹, based on a quantity introduced earlier,⁴⁵, to characterize complete exchange of the local environment for a given villin molecule. In the 64-villin trajectory we found that more than half of the villins in the 64-villin system experienced at least one complete swap of the local environment. This finding also supports that the long time diffusion regime has been reached. As further illustration, Movie S1 shows the center-of-mass motion of selected villins and how one villin escapes from one cage and diffuses freely as a monomer and then enters another cage in the simulation. Another factor influencing the results may be finite-size effects, however, the results with the 8-copy and 64-copy are qualitatively similar with the quantitative differences assumed to be due to the formation of larger clusters in the 64-copy system as discussed above. Therefore, it is unlikely that the lack of clear two time regimes is due to insufficient simulation length or finite-size effects. Instead, it appears that almost uniform diffusion from picoseconds to at least microseconds is a feature of this system and a result of extensive cluster formation.

Rotational Diffusion of Villin

In the crowded systems the rotational correlation functions based on the reorientation of vectors attached to the molecular frame (see Methods) were calculated for each protein copy separately. As Figure 4 shows, there is significant variation between the correlation decays in different copies and especially at the highest concentration, some correlation functions display non-exponential behavior that we attribute to the inhomogeneity of local environment and limited statistics. In the following discussion, we focus on averages over individual protein copies.

Figure 4.

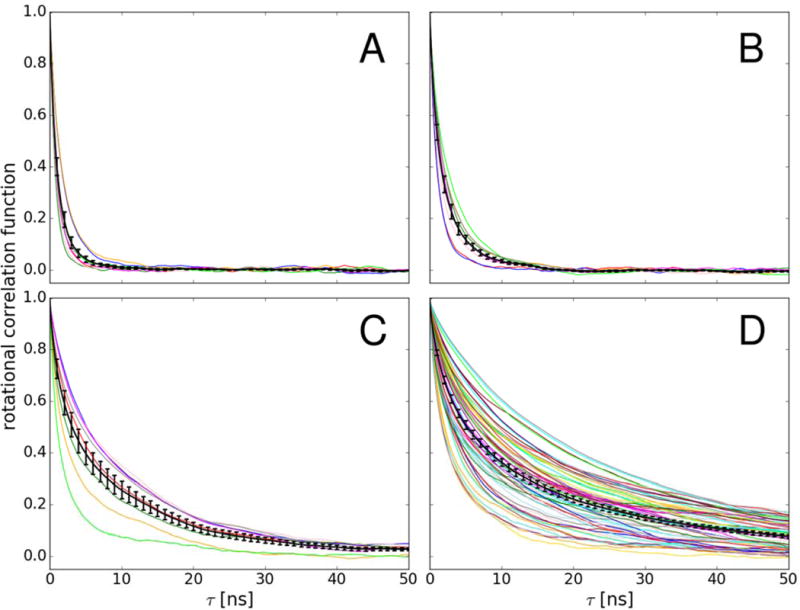
Correlation functions for scalar product between random vectors fixed to the molecular frame used for describing rotational diffusion (see Methods) of individual villin copies (color lines) at 8 mM (A), 16 mM (B), 32 mM with eight copies (C), and 32 mM with 64 copies (D). Correlation functions averaged over villin copies are shown with error bars (black lines).

The correlation functions were fit with a double-exponential with two time scales. The fits to the average correlation functions (black lines in Figure 4) are shown in Figure 5. For the highest concentration solutions, we also fitted a triple-exponential function (Eq. 12) to better represent the initial decay of the correlation functions. Anisotropy in rotational diffusion was not considered here. The resulting double-exponential fit parameters averaged over fits of individual correlation functions are given in Table 3. The results for the triple-exponential fit to the average correlation functions for the 64-copy 32mM system are:τ_Rf = 0.845 ns, τ_Rm = 5.762 ns, and τ_Rs = 29.596 with the weights S_Rm² = 0.390 and S_Rs² = 0.200 resulting in Dr=0.011 nm²/ns, which is similar to the result from the double-exponential fit. The dilute value is again about three times faster than the value of D_r = 0.068 ns⁻¹ obtained from HYDROPRO due to the underestimated viscosity with the TIP3P water model.

Figure 5.

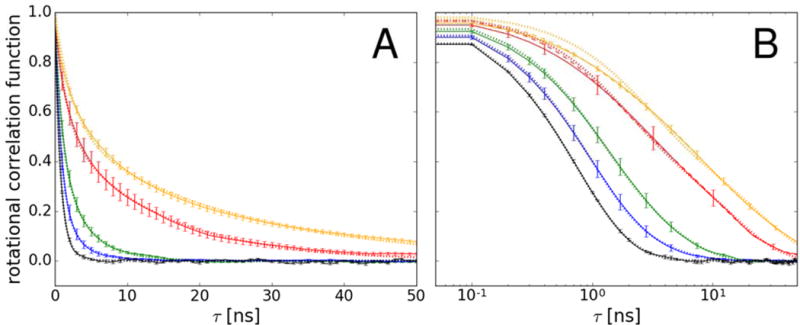
Correlation functions for scalar product between random vectors fixed to the molecular frame used for describing rotational diffusion (see Methods) averaged over villin copies at 8 mM (blue), 16 mM (green), and 32 mM (eight-copy: red; 64-copy: orange). Villin in dilute solvent is shown as a black line (averaged over trajectory blocks). Exponential functions fit to the average correlation functions are shown as dotted lines. Triple-exponential fits (at 32 mM with 8 and 64 protein copies) are shown as dashed lines (B). All fits have R² values of larger than 0.995 and χ² values of less than 0.05. Values of τ are shown in regular (A) and logarithmic (B) scales.

Table 3.

Rotational diffusion parameters of villin at different concentrations

[villin] (mM)	Np	τRf (ns)	τRf−1 (ns−1)	τRs (ns)	τRs−1 (ns−1)	SR2	τ (ns−1)	τini (ns−1)	Dr (ns−1)	Dr,ini (ns−1)	Dr slow-down	Dr, ini slow-down
dilute	1	0.59 (0.08)	1.870 (0.321)	1.48 (0.45)	0.887 (0.181)	0.49 (0.13)	0.820 (0.026)	0.722 (0.022)	0.204 (0.006)	0.232 (0.007)	1	1
8	8	0.97 (0.13)	1.142 (0.110)	3.96 (0.93)	0.342 (0.052)	0.17 (0.03)	1.388 (0.180)	1.095 (0.128)	0.134 (0.014)	0.166 (0.015)	0.65	0.72
16	8	1.00 (0.09)	1.069 (0.099)	3.80 (0.21)	0.271 (0.016)	0.42 (0.05)	2.223 (0.207)	1.489 (0.118)	0.082 (0.009)	0.119 (0.011)	0.41	0.51
32	8	1.83 (0.20)	0.601 (0.065)	13.81 (0.81)	0.075 (0.005)	0.52 (0.06)	8.151 (0.910)	3.574 (0.487)	0.024 (0.004)	0.057 (0.010)	0.12	0.25
32	64	2.70 (0.15)	0.445 (0.023)	24.50 (1.07)	0.047 (0.003)	0.54 (0.02)	14.445 (0.721)	5.550 (0.369)	0.014 (0.001)	0.038 (0.002)	0.07	0.16

Fast (τ_Rf) and slow (τ_Rs) correlation times and S_R² weight as in Eq. 8. Averaged inverse tumbling times are reported as well. Total tumbling times τ and τ_ini were obtained according to Eqs. 10 and 11. Rotational diffusion coefficients D_r and D_r,ini were obtained according to Eq. 9. Error estimates are given in parentheses and the slow-down is relative to rotation in dilute solvent.

As the concentration increases in the lower range (8 – 16 mM), the contribution to the overall diffusion, described by S_R², shifts toward the slow time scales, whereas, the fast, τ_Rf, and the slow, τ_Rs, correlation times remain mostly constant. In the higher concentration range (16 – 32 mM), both τ_Rf and S_R² are relatively unaltered, whereas τ_Rs significantly increases. This is generally consistent with observations from NMR studies for the same systems.⁷⁶ The resulting values of D_r decrease with increasing concentrations. We are reporting results both based on linear averaging of tumbling times according to Eq. 10 and averaging of inverse tumbling times according to Eq. 11. The latter quantity is more commonly discussed when analyzing experiments such as depolarized dynamic light scattering and focuses on the initial decay slope. One interpretation of this data is that as the solutions become denser, a diminishing fraction of villin rotates as a free monomer, while the remaining villin copies experience increasing crowding effects that cause the formation of larger clusters. Interestingly, the rotational diffusion slows down more significantly at higher concentrations (to 16% of dilute value at 32mM based on averaging inverse tumbling times) than the translational diffusion (48–56% of dilute value at 32mM). This generally agrees with the results from the Pielak group for crowded systems involving weakly interacting proteins¹⁵, but it differs from results from the Saalwächter group⁶⁸ where rotational properties of largely non-interacting proteins were studied. This may be expected as the decoupling between translational and rotational diffusion under crowding conditions has been suggested to be protein-specific, although methodological differences may also play a role.⁶⁸

Transient Cluster Formation

At high concentrations, frequent encounters between proteins are unavoidable. The previous analysis is already suggesting that such interactions may lead to transient clusters and we analyzed this aspect further. The interactions between the proteins were characterized by the calculations of an average number of contacts a single protein forms with others. The results are summarized in Table 4. The number of contacts doubled when the concentration increased from 8 to 16 mM, and rose by another 50% when the concentration increased further from 16 to 32 mM. To shed light on the nature of the interactions governing the contacts formation, we compared with coarse-grained (CG) simulations, where residues were assigned purely attractive, neutral, or repulsive interactions (see Methods section for more details) (Table 4). We find that the number of contacts in the all-atom simulations is roughly one order of magnitude larger than in the CG model with neutral interactions but still significantly less than with purely attractive interactions. We note that the available volume at any of the concentrations does not force interactions as there were no protein-protein contacts in the CG simulations with the repulsive potential. This comparison suggests that the villin interactions are weakly attractive.

Table 4.

Average number of contacts per protein obtained from all-atom and CG simulations

[villin] (mM)	all-atom	CG attractive	CG neutral	CG repulsive
8	0.48 (0.13)	3.73 (0.32)	0.065 (0.005)	0.00 (0.00)
16	0.94 (0.12)	3.90 (0.33)	0.093 (0.011)	0.00 (0.00)
32	1.46a (0.19); 2.05b (0.07)	3.85 (0.23)	0.229 (0.016)	0.00 (0.00)

^aeight copies,

^b64 copies

The weak attraction led to transient cluster formation. Fig. 6 shows the size of clusters as a function of concentration. At 8 mM, 60% of the proteins exist as monomers but there is a small fraction of dimers, trimers, and tetramers. At 16 mM, the fraction of monomers decreases to 35% and clusters as large as hexamers are observed. At 32 mM, the eight-copy system is too small to adequately characterize the cluster distribution. In the 64-copy system, we find significant fractions of clusters as large as 45-mers while the fraction of monomers is decreased to less than 10%. Since larger clusters than 50-mers were not observed, we conclude that villin still remains soluble at 32 mM in the simulations but higher-order clusters are present in the simulations with non-negligible fractions. The average cluster size in the 64-copy system, N_c, is 13, a number that is close to N_c = 3–5, previous SAXS experimental values for lysozyme at a volume fraction of 0.1.³⁴ Given the differences in proteins, protein sizes and protein-protein interactions, this is reasonable qualitative agreement. Furthermore, the average number of contacts obtained at 32 mM from 64 protein copies system (Table 4), i.e. 2.05±0.07, corresponds well to the maximum number of neighbors (2) determined from colloids interacting by the centrosymmetric potential as well as patchy colloids at the volume fraction ϕ = 0.1.⁴¹

Figure 6.

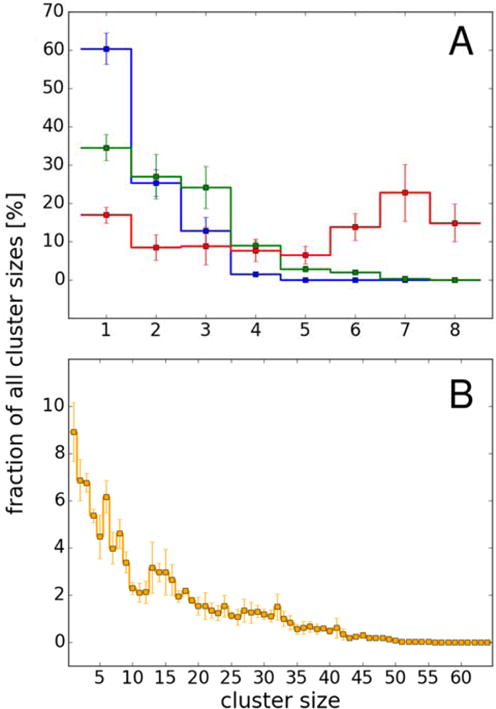
Distribution of cluster sizes for simulations of eight proteins (A) at 8 mM (blue), 16 mM (green) and 32 mM (red) and of 64-copy system (B) at 32 mM based on contacts defined as Cα-Cα distances of less than 0.7 nm (see Methods).

Villin is not known to form specific clusters and we also did not find a strong preference for specific complexes as the population of cluster structures for a given cluster size is quite diverse (see Fig. S5). However, according to our simulations, certain parts of the villin structure are more likely to be involved in the protein-protein interfaces than others (see Fig. 7). Favorable interactions were found for the residues belonging to the N-terminal α-helix (residues 5–10) and the last few residues at the C-terminus. The contact maps are in rough agreement with a previous simulation study of villin contacts in a crowded mixture of villin and protein G.⁹ When mapped onto the three-dimensional villin fold (Fig. 8A), it becomes apparent that there is a preference for one side of the structure to interact. The residues involved in these interactions are largely acidic and basic suggesting that the interactions that lead to non-specific clusters are driven more by electrostatics and salt-bridge formation than by hydrophobic interactions. These interactions can also partially explain the observed weak concentration-dependency of specific regions in S_l² (see Fig. 2). Favorable interactions at residues 5–10 and at the C-terminus are enhanced as the concentration increases. Enhanced interactions result in the decreased flexibility at residues 5–10. In contrast, favorable interactions at the C-terminus result in the increased flexibility at the C-terminus. The difference is that, bulkier residues are facing outward at the C-terminus (e.g. Phe36) but those residues are facing inward at residues 5–10 (e.g. Phe7), interacting with other phenylalanines (Phe11 and Phe18). In the crowded environment, favorable interactions at residues 5–10 are strengthened without being affected by Phe7 but these residues are weakened by a flexible Phe36. Also in residues 11–14, crowding partially affects the stability of the three interacting phenylalanines, so the flexibility in this region increases (See Fig. 2 and 8B).

Figure 7.

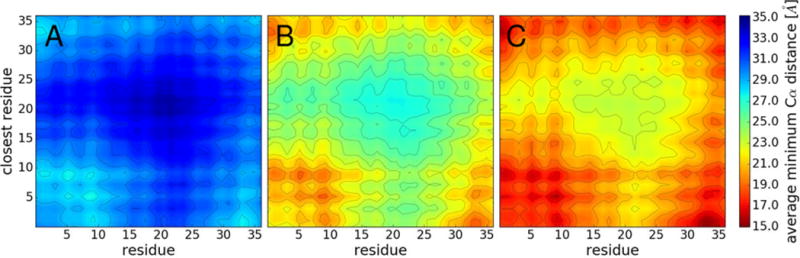
Contact map of residues between proteins at 8 mM (A), 16 mM (B), and 32 mM (C). Colors indicate the average Cα distances from a given residue to the closest residue of another nearby villin molecule. Residue numbers 1–36 correspond to 41–76 in the biological sequence.

Figure 8.

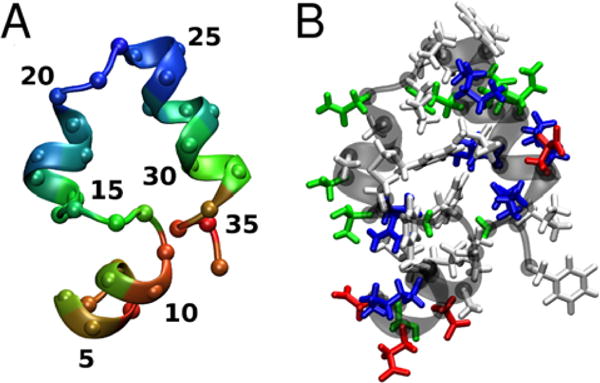
Structure of villin colored according to the average Cα distance to nearby villin molecules (A) (short: red, medium: green, long: blue) and by residue type (B) (hydrophobic: white, polar: green, acidic: red, basic: blue). Residue numbers 1–36 correspond to 41–76 in the biological sequence.

Although the range of minimum distance decreases with increasing concentration (Fig. 7) the pattern of favorable contact is very similar at all three concentrations. The contact maps obtained at 32 mM concentration with eight (Fig. 7C) and 64 (Fig. S7) protein copies are also in good agreement suggesting that contact preferences are not sensitive to finite-size effects.

The kinetic nature of cluster formation was characterized by defining a conditional contact function as given in Eq. S3 and fitting a triple-exponential function. The results in Table 5 reveal three distinct time scales: 0.74–1.9 ns, 12.5–42.0 ns, and 108–342 ns. The longest time scale contributes most at the lowest and medium concentrations, but at the highest concentration the contribution from all the three time scales is comparable. Furthermore, if the 8-copy 32 mM results are excluded, which may be too small to obtain reliable statistics, the longest time scale clearly increases with concentration as may be expected, but even at 32mM, cluster formation remains highly transient. However, clusters form mostly on time scales that are long (τ_c^l) compared to characteristic rotational time scales of 1–25 ns (see Table 3) and the time it takes to diffuse by the size of villin (on the order of 10 ns; based on data in Table 2). Therefore, although cluster formation is dynamic, clusters persist long enough to significantly affect diffusional properties. This prevents a pronounced cage effect for single villins as they frequently associate with other molecules rather than moving independently in a cage of surrounding crowders. On the other hand, a cage affect at the larger cluster level is also prevented because clusters frequently reorganize and do not persist long enough to experience diffusion on different time scales. As a result, the effective diffusion of villin becomes less time-dependent than standard colloid theory would predict as discussed above.

Table 5.

Time scales of contact formation

C [mM]	τcs [ns]	τcm [ns]	τcl [ns]	Scs	Scm	Scl
8	1.084	38.279	108.374	0.287	0.096	0.617
16	0.740	12.490	242.680	0.263	0.217	0.520
32 (#8)	1.044	19.069	149.563	0.323	0.191	0.486
32 (#64)	1.882	42.043	341.801	0.374	0.295	0.331

Short (τ_c^s), medium (τ_c^m), and long (τ_c^l) correlation times of contacts between proteins along with the corresponding weights S_c^s, S_c^m, and S_c^l obtained from fitting a triple-exponential to a correlation function based on conditional contact formation (Eq. S3).

The longest obtained time scales of contact formation between villins are consistent with findings for lysozyme solutions studied by neutron spin-echo spectroscopy (NSE) that set the lower limit of the cluster lifetime to 25 ns²⁹. Other studies show that the lifetime of lysozyme clusters is finite on millisecond time scales^{77, 78}. The presented lifetimes are also not in contradiction with reports for solutions of bovine β-lactoglobulin (BLG) that indicate that BLG clusters are static on NSE observation time scale, i.e. up to 50 ns³³, but have a limited lifetime on the microsecond observation time scale of dynamic light scattering³³.

Diffusion Slow-Down as a Consequence of Cluster Formation

The simulation results present a picture where villin molecules engage in the formation of transient clusters that persist on time scales on the same order or larger than rotational and translational diffusion time scales. This suggests that the observed slow-down in diffusion for the villin system is largely related to cluster formation.

We extracted representative structures of clusters of different sizes from the trajectories and estimated their translational and rotational diffusion coefficients via HYDROPRO.⁷⁵ The resulting diffusion coefficients as a function of cluster size are shown in Fig. S6. D_r decreases more sharply with increasing clusters size than D_t. We then estimated overall diffusion coefficients by summing the cluster-size dependent diffusion coefficients with weights according to the cluster distributions observed in the simulations (see Fig. 6). The results are shown in Table 6 in comparison with the values of D_t and D_r extracted from the simulations. For translational diffusion, there is close agreement between the cluster-based estimates and the actual MD diffusion rates. Rotational diffusion rates also match well. Best agreement is found with the linear-average rotational diffusion constants for lower concentrations but with the inverse tumbling time averages at 32 mM villin concentration. This indicates that additional factors may affect rotational diffusion beyond simple cluster formation such as reduced solvent viscosity due to crowding or electrostatic friction. As electrostatic friction may be orientationally dependent, this could explain the larger discrepancy for rotational than for translational diffusion between the MD-derived results and the cluster-based estimates. Finally, a simple cluster-based estimate of rotational diffusion also does not reflect the significant heterogeneity and overall non-exponentiality seen in the rotational correlation functions for individual copies at the highest concentration (see Fig. 4) which may explain additional discrepancies.

Table 6.

Translation and rotational diffusion based on transient clusters

C [mM]	Np	Dt,MD* [nm2/ns]	Dt,cluster [nm2/ns]	Dr,MD* [ns−1]	Dr,ini,MD* [ns−1]	Dr,cluster [ns−1]
8	8	0.16 (0.006)	0.16 (0.002)	0.053 (0.006)	0.065 (0.006)	0.051 (0.002)
16	8	0.12 (0.004)	0.14 (0.003)	0.032 (0.004)	0.047 (0.004)	0.038 (0.002)
32	8	0.09 (0.005)	0.11 (0.003)	0.0095 (0.0017)	0.022 (0.004)	0.020 (0.001)
32	64	0.062 (0.002)	0.079 (0.012)	0.0057 (0.0004)	0.015 (0.0008)	0.013 (0.002)

Translational (D_t) and rotational (D_r) diffusion calculated either directly from the simulations (D_t,MD for 10–100 ns and D_r,MD) or as a sum of cluster-size dependent diffusion weighted by the observed cluster distributions (D_t,cluster and D_r,cluster);

^*values extracted from the MD simulations (see Tables 2 and 3) were divided by η_exp/η_TIP3P=2.54 to correct for overestimated diffusion with the TIP3P water model.

CONCLUSIONS

We describe out all-atom MD simulations of crowded villin systems in explicit solvent at different concentrations. Simulations of crowded protein systems remain challenging and we had to increase the strength of protein-water interactions to obtain good agreements with experiments.

After adjusting the force field, we found that both, translational and rotational diffusion, slow down to different extents in the crowded environment. Rotational diffusion is slowed down more significantly apparently because of the transient formation of clusters. In the simulations, we observe cluster formation due to weakly attractive but mostly non-specific interactions between villins. As the concentration increases, the distribution of clusters shifts towards higher-order clusters at higher concentrations but the peak of the distribution remains at monomers, suggesting that villin is still soluble in the simulations. The transient cluster formation also appears to be responsible for a lack of the typical cage effect expected for colloids that is manifest by two distinct diffusive regimes but not strongly present for the villin system studied here.

When we predicted diffusion coefficients from clusters observed in the simulations and weigh those values according to the observed cluster fractions, we largely reproduce the overall observed translational and rotational diffusion coefficients. This suggests that the slow-down in diffusion is primarily due to transient cluster formation rather than reduced solvent viscosity or other types of molecular friction. The observed rotational diffusion does not fully match the cluster-based estimates suggesting that additional factors are involved, with electrostatic friction being the most likely explanation. This aspect will be investigated in more detail in future studies.

Although we studied only villin here, we assume that the findings have broader implications for diffusive properties in crowded cellular environments. Essentially, the finding is that diffusion depends largely on transient cluster formation, which in turn depends on the strength of interactions between different macromolecules and ultimately the surface amino acid composition. Therefore, experimental studies could probe this aspect by determining diffusion rates for proteins with sequence variants that alter their surface properties.

The differential slow-down in rotational and translational diffusion rates is interesting and may have some implications for diffusion of proteins and ligands in a cell. In diffusion-limited enzymatic reactions, relatively slower rotational diffusion would allow enzymes to remain pre-oriented, especially when part of metabolic pathways and thereby increase metabolic efficiencies. On the other hand, the apparent prevalence of weak attractive interactions allows for related metabolic enzymes to be close so that products of one enzyme can quickly find the active site of the next enzyme in a given pathway. However, since we only studied villin here, further studies of metabolic enzymes in the presence of ligands will be needed to test these ideas.