Fig. 3.

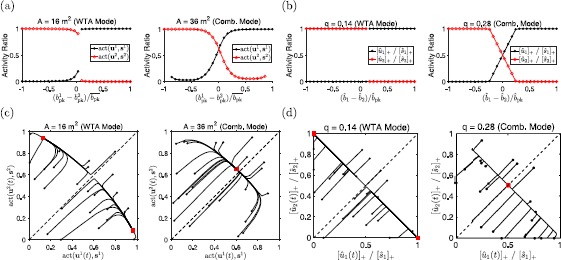
Comparison of the operational modes of the full and reduced models. (a) The full megamap with optimal weights is driven by the conflicting external input, $\mathbf{\text{b}}=(1/\overline{b_{\mathrm{pk}}})(b_{\mathrm{pk}}^1\overline{\mathbf{\text{b}}}({\mathbf{\text{x}}}_1)+b_{\mathrm{pk}}^2\overline{\mathbf{\text{b}}}({\mathbf{\text{x}}}_2))$, where $\overline{\mathbf{\text{b}}}({\mathbf{\text{x}}}_k)$ is the training input into location ${\mathbf{\text{x}}}_k$ (Eq. (2)). For the relatively small megamap operating in the WTA mode (left, Fig. 1(c)), any equilibrium activity bump fully represents one location while effectively ignoring the input for the other location. For the large megamap operating in the combinatorial mode (right, Fig. 1(d)), the equilibrium activity bump fully represents one location when $|b_{\mathrm{pk}}^1-b_{\mathrm{pk}}^2|$ is sufficiently large. Otherwise, the equilibrium state corresponds to a linear combination of the two embedded activity bumps, amplifying the difference in input strengths. The initial state for all simulations corresponds to $\overline{\mathbf{\text{f}}}({\mathbf{\text{x}}}_2)$ (Eq. (2)). The activity ratio is given by $act({\mathbf{\text{u}}}^k,{\mathbf{\text{s}}}^k)\equiv {\sum }_{i\in \overline{S_k}}f(u_i)/{\sum }_{i\in \overline{S_k}}f(s_i^k)$, where $u_i$ and $s_i^k$ are the equilibrium states of cell i given the conflicting external input, $b_i$, and the isolated input, $(b_{\mathrm{pk}}^k/\overline{b_{\mathrm{pk}}}){\bar{b}}_i({\mathbf{\text{x}}}_k)$, respectively. Data points were omitted if $f({\mathbf{\text{s}}}^k)$ was not an activity bump over location ${\mathbf{\text{x}}}_k$, which occurs in this example when $b_{\mathrm{pk}}^k\approx 0$. (b) The 2-unit model responds similarly to the conflicting external input. The parameters $w^0=1.2$ and q are comparable to the corresponding reduced weights of the megamap (Eq. (7), Fig. 2(e)). The reduced inhibitory weight, ${\hat{w}}^{\mathrm{I}}=5.3$, and threshold, $\theta =0.9$, are the exact values corresponding to the megamap parameters in (a). (c) The initial state (black circles) is varied randomly, and the external input is constant ($b_{\mathrm{pk}}^1=b_{\mathrm{pk}}^2=\overline{b_{\mathrm{pk}}}/2$). The equilibrium state reached (red squares) depends on the initial state for the small megamap but not for the large megamap. (d) The 2-unit model with the same parameters as used in (b) similarly shows hysteresis only in the WTA mode. Here, ${\hat{b}}_1={\hat{b}}_2={\hat{b}}_{\mathrm{pk}}/2$