Improved estimation of subject-level functional connectivity using full and partial correlation with empirical Bayes shrinkage

Abstract

Reliability of sub ject-level resting-state functional connectivity (FC) is determined in part by the statistical techniques employed in its estimation. Methods that pool information across subjects to inform estimation of subject-level effects (e.g., Bayesian approaches) have been shown to enhance reliability of subject-level FC. However, fully Bayesian approaches are computationally demanding, while empirical Bayesian approaches typically rely on using repeated measures to estimate the variance components in the model. Here, we avoid the need for repeated measures by proposing a novel measurement error model for FC describing the different sources of variance and error, which we use to perform empirical Bayes shrinkage of subject-level FC towards the group average. In addition, since the traditional intra-class correlation coefficient (ICC) is inappropriate for biased estimates, we propose a new reliability measure denoted the mean squared error intra-class correlation coefficient (ICC_MSE) to properly assess the reliability of the resulting (biased) estimates. We apply the proposed techniques to test-retest resting-state fMRI data on 461 subjects from the Human Connectome Project to estimate connectivity between 100 regions identified through independent components analysis (ICA). We consider both correlation and partial correlation as the measure of FC and assess the benefit of shrinkage for each measure, as well as the effects of scan duration. We find that shrinkage estimates of subject-level FC exhibit substantially greater reliability than traditional estimates across various scan durations, even for the most reliable connections and regardless of connectivity measure. Additionally, we find partial correlation reliability to be highly sensitive to the choice of penalty term, and to be generally worse than that of full correlations except for certain connections and a narrow range of penalty values. This suggests that the penalty needs to be chosen carefully when using partial correlations.

1 Introduction

Measurement reliability is a persistent concern in psychological science (Button et al., 2013; Munafò et al., 2014; Collaboration, 2015). Functional connectivity (FC) of the brain, as measured using resting-state functional magnetic resonance imaging (rs-fMRI), is no exception (Shehzad et al., 2009). Driven by the growing role of subject-level FC estimates in fingerprinting (Finn et al., 2015; Airan et al., 2016), precision functional connectomics (Gordon et al., 2017), brain-behavior studies (Smith et al., 2015), and surgical planning (Tie et al., 2014), determining the best practices for reliable estimation of FC is an important and ongoing topic of research (e.g., Anderson et al., 2011; Birn et al., 2013; Laumann et al., 2015; Noble et al., 2017b). An analysis technique that has been shown to improve reliability of subject-level FC and related measures is shrinkage, a statistical estimation method in which individual observations “borrow strength” from a larger group of observations (Su et al., 2008; Varoquaux et al., 2010; Shou et al., 2014; Mejia et al., 2015; Dai et al., 2016; Chong et al., 2017; Rahim et al., 2017).

Shrinkage belongs to the more general family of Bayesian approaches. Fully Bayesian approaches, such as that proposed by Warnick et al. (2017), use a latent variable model in which the unknown connectivity for each subject gives rise to the unobserved “true” time series plus random noise, and subjects are drawn from some population distribution. In this framework, prior distributions are assumed on the parameters controlling the population distribution and the random noise, including the variance within and across subjects. Bayesian computation techniques like Markov chain Monte Carlo (MCMC) or variational Bayes (VB) are used to estimate or sample from the posterior distribution of each parameter and latent variable in the model. The posterior distribution of the connectivity for each subject can then be used to obtain estimates through the posterior mode as well as inference through the posterior quantiles.

Since fully Bayesian approaches tend to be computationally intensive, empirical Bayesian approaches are often employed as an efficient and convenient alternative. In the empirical Bayesian framework, certain parameters are estimated a-priori using the data or prior knowledge obtained from existing studies. Given these parameter estimates, the desired posterior quantities often have a closed-form solution, greatly facilitating computation. Empirical Bayes shrinkage estimators are an example of this approach and result from assuming a measurement error model on a set of estimates. For example, in our case of a Gaussian population prior with independent Gaussian errors, the empirical Bayes shrinkage estimates are weighted combinations of the subject-level observation and the group average, where the degree of shrinkage towards the group average that gives rise to the posterior mean and minimizes mean squared error (MSE) relative to the truth is equal to the ratio of within-subject variance to total (within-subject plus between-subject) variance (James and Stein, 1961; Efron and Morris, 1975). Therefore, lower within-subject variance combined with higher between-subject variance leads to less shrinkage of subject-level estimates toward the group, while higher within-subject variance and lower between-subject variance leads to greater shrinkage.

Previous work has clearly illustrated the benefits of shrinkage, with 25–30% gain in reliability of subject-level connectivity (Varoquaux et al., 2010; Shou et al., 2014; Dai et al., 2016; Rahim et al., 2017) and parcellations (Mejia et al., 2015; Chong et al., 2017). However, estimating the relevant variance components to determine the degree of shrinkage has typically relied on having access to repeated measures through test-retest fMRI data. This limits the applicability of shrinkage methods, since in many studies only a single rs-fMRI session is available for most if not all subjects, and even if multiple sessions were available one would want to utilize the full data available for each subject to improve estimation.

In this work, we propose a novel method to compute empirical Bayes shrinkage estimates of FC, where the degree of shrinkage is determined using single-session fMRI data. Previous work has proposed using “pseudo test-retest” data, in which a single scanning session is split into two contiguous sub-sessions, as a proxy for inter-session variance (Mejia et al., 2015; Mueller et al., 2015). However, this will tend to overestimate the sampling variance of FC, since fewer time points are used in its estimation. In Mejia et al. (2015), we proposed using an empirically determined adjustment factor to correct for this, but the generalizability of such an approach is limited. Here, we instead propose a measurement error model for FC and describe how this model can be used to estimate within-subject variance of FC using single-session fMRI data. Leveraging recent developments in the study of moment-to-moment changes in FC, this model assumes that within-subject variance of FC comes not only from sampling error, but from changes in true FC over time, i.e. dynamic connectivity (Allen et al., 2014). The measurement error model, resulting shrinkage estimator, and variance component estimation techniques are described in Section 2.1.

Assessing the reliability of shrinkage estimates is also a challenge, since the intra-class correlation coefficient (ICC), a commonly used and interpretable reliability metric, is not appropriate for biased estimators. Therefore, most reliability studies for shrinkage estimates have relied on mean squared error (MSE) using simulations or test-retest fMRI data to illustrate the gains in reliability due to shrinkage. However, MSE is sensitive to measurement scale and lacks the convenient interpretation of ICC, which ranges from 0 to 1 and represents the proportion of variance in the observations due to true between-subject differences rather than within-subject error or deviation. We therefore propose combining ICC and MSE into a novel reliability measure for biased or unbiased estimators, ICC_MSE. ICC_MSE is equal to ICC for unbiased estimators but is also appropriate for biased estimators and allows for fair and intuitive comparison between shrinkage and traditional estimators. We motivate and describe this measure in Section 2.2.

Finally, we explore the role of scan duration in reliability of both shrinkage and traditional estimates of FC, as the effect of scan duration on reliability of FC is a topic of much recent interest (e.g., Shehzad et al., 2009; Van Dijk et al., 2010; Anderson et al., 2011; Birn et al., 2013; Laumann et al., 2015; Noble et al., 2017a). Several recent studies have also observed substantial differences in reliability across connections. For example, connections within the default mode network (DMN) have been found to exhibit particularly high reliability even for short scan duration, while connections involving the motor network tend to exhibit poor reliability (Shehzad et al., 2009; Van Dijk et al., 2010; Anderson et al., 2011; Laumann et al., 2015; Mueller et al., 2015; Finn et al., 2015). Therefore, we also explore the relationship between scan duration and reliability for connections within different resting-state networks. In addition, most of the extant literature on the relationship between scan duration and FC reliability uses Pearson correlation coefficients as the primary measure of the degree of connectivity between brain regions. The issue of sufficient scan duration deserves greater investigation in the context of partial correlations, which are becoming increasingly popular for their ability to distinguish between brain regions that are directly versus indirectly correlated (Smith et al., 2011; Varoquaux and Craddock, 2013; Smith et al., 2015; Wang et al., 2016).

We perform a reliability analysis using data from the Human Connectome Project (HCP) to examine the role of scan duration, shrinkage, and connectivity measure (full and partial correlation) on reliability of functional connectivity. The HCP is ideal for this analysis due to its large sample size and relatively long duration of rs-fMRI scans. We assess reliability at multiple levels: omnibus reliability over all connections, reliability of within-network connections, reliability of all connections with a particular seed, and reliability of individual connections. This multi-resolution approach provides a more complete picture of reliability and illustrates that reliability of FC is more compex than a single measure can detect. For estimating partial correlations through ridge regression, we first perform a reliability study to assess the impact of the regularization parameter, ρ. We find that certain values of ρ lead to partial correlation estimates with improved reliability for particular connections but worse reliability overall compared with full correlations. Notably, we find that common choices of ρ, such as 0.01, lead to partial correlations with much worse reliability than full correlations. The reliability study is described in Section 3, and we conclude with a discussion in Section 4.

2 Methods

2.1 Empirical Bayes shrinkage using single-session data

Let q = 1, …, Q index the nodes (voxels, vertices or regions) between which we wish to estimate pairwise connectivity, and consider a single pair of nodes q and q′. The overall estimate of FC obtained from an fMRI session is often referred to as static connectivity, in contrast to dynamic connectivity across the session. As we describe in the next section, considering static connectivity as an average over a dynamic connectivity time series enables us to use the central limit theorem to model and estimate the relevant variance components. Hereafter, the measure of FC is assumed to be Fisher-transformed correlation or partial correlation.

2.1.1 A measurement error model for functional connectivity

Assume here that all subjects have the same scan duration, and let $\mathcal{T}=\left\{1,\dots ,T\right\}$ index the fMRI time series for each subject (see Appendix A for the case when subjects have differing scan duration). Let x_i,t(q, q′) be the unobserved true connectivity between q and q′ at time $t\in \mathcal{T}$, which we can write as x_i,t(q, q′) = μ_i(q, q′) + δ_i,t(q, q′), where μ_i(q, q′) is the long-term average connectivity for subject i, and δ_i,_t(q, q′) represents dynamic fluctuations in connectivity over time. Since fMRI data contains noise, the observed or estimated connectivity w_i,t(q, q′) at time t can be written as the truth x_i,t(q, q′) plus noise ε_i,t(q, q′), that is

$$w_{i,t}\left(q,q^{\prime }\right)=x_{i,t}\left(q,q^{\prime }\right)+{\epsilon }_{i,t}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,t}\left(q,q^{\prime }\right)+{\epsilon }_{i,t}\left(q,q^{\prime }\right).$$

We assume that ${\mu }_i\left(q,q^{\prime }\right)~N\left\{\mu \left(q,q^{\prime }\right),{\sigma }_{\mu }^2\left(q,q^{\prime }\right)\right\}$, where μ(q, q′) is the average population-level connectivity between q and q′ and ${\sigma }_{\mu }^2\left(q,q^{\prime }\right)$ is its between-subject variance, and that ${\delta }_{i,t}\left(q,q^{\prime }\right)~\left\{0,{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right\}$ and ${\epsilon }_{i,t}\left(q,q^{\prime }\right)~\left\{0,{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\}$. Since the connectivity measures are Fisher-transformed correlations, it is reasonable to assume that δ_i,t(q, q′) and ε_i,t(q, q′) are independent, although each may exhibit autocorrelation due to temporal dependence in fMRI data.

For analyses of static connectivity, we do not actually estimate the dynamic time series of connectivity, but rather its average across the fMRI session $\mathcal{T}$, which can be written

$$w_{i,\mathcal{T}}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,\mathcal{T}}\left(q,q^{\prime }\right)+{\epsilon }_{i,\mathcal{T}}\left(q,q^{\prime }\right),$$ (1)

where by the central limit theorem for dependent observations, ${\delta }_{i,\mathcal{T}}\left(q,q^{\prime }\right)$ and ${\epsilon }_{i,\mathcal{T}}\left(q,q^{\prime }\right)$ are approximately distributed

$$\begin{gathered} {\delta }_{i,\mathcal{T}}\left(q,q^{\prime }\right)=\frac{1}{T}{\displaystyle \sum _{t=1}^T{\delta }_{i,t}\left(q,q^{\prime }\right)~N\left\{0,T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right\}\text{and}} \\ {\epsilon }_{i,\mathcal{T}}\left(q,q^{\prime }\right)=\frac{1}{T}{\displaystyle \sum _{t=1}^T{\epsilon }_{i,t}\left(q,q^{\prime }\right)~N\left\{0,T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\}}. \end{gathered}$$

Here, T_δ = T/τ_δ is the effective sample size (ESS) of the timeseries ${\left\{{\delta }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in \mathcal{T}}$, and T_ε = T/τ_ε is the ESS of ${\left\{{\epsilon }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in \mathcal{T}}$, where τ_δ and τ_ε are the unknown autocorrelation times of ${\left\{{\delta }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in \mathcal{T}}$ and ${\left\{{\epsilon }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in \mathcal{T}}$, respectively (Kass et al., 1998; Thompson, 2011; Gong and Flegal, 2016). Various techniques exist for estimating autocorrelation time, and in the case of an autoregressive (AR) process, there is a closed-form solution involving only the partial autocorrelation function of the process (Thompson, 2011); however, the proposed shrinkage methods described below do not require estimation of τ_δ or τ_ε.

Equation (1) describes a measurement error model for static connectivity estimated from an fMRI time series of length T. The variance components are $T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)$, the within-subject, across-session variance of true connectivity; $T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)$, the within-subject sampling variance; and ${\sigma }_{\mu }^2\left(q,q^{\prime }\right)=:{\sigma }_{\mathit{between}}^2\left(q,q^{\prime }\right)$, the between-subject variance. The total within-subject variance is therefore ${\sigma }_{\mathit{within}}^2\left(q,q^{\prime }\right):=T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)$. The empirical Bayes shrinkage estimator of μ_i(q, q′) is given as in Morris (1983) by

$${\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)=\lambda \left(q,q^{\prime }\right){\overline{w}}_{\mathcal{T}}\left(q,q^{\prime }\right)+\left\{1-\lambda \left(q,q^{\prime }\right)\right\}{w}_{i,\mathcal{T}}\left(q,q^{\prime }\right),$$

where ${\overline{w}}_{\mathcal{T}}\left(q,q^{\prime }\right)=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{w}_{i,\mathcal{T}}\left(q,q^{\prime }\right)}$ is the estimated population average connectivity, and the degree of shrinkage λ(q, q′) is equal to the ratio of within-subject variance to total (within-subject plus between-subject) variance of $w_{i,\mathcal{T}}\left(q,q^{\prime }\right)$, given by

$$\lambda \left(q,q^{\prime }\right)=\frac{{\sigma }_{\mathit{within}}^2\left(q,q^{\prime }\right)}{{\sigma }_{\mathit{within}}^2\left(q,q^{\prime }\right)+{\sigma }_{\mathit{between}}^2\left(q,q^{\prime }\right)}=\frac{T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)}{T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)+{\sigma }_{\mu }^2\left(q,q^{\prime }\right)},$$ (2)

We now describe how to estimate the relevant variance components to achieve the optimal degree of shrinkage, which minimizes MSE of the resulting estimates relative to the truth.

2.1.2 Variance component estimation

The total variance on the denominator of λ(q, q′) is easily estimated as $Va{r}_i\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}$. If a second fMRI session ${\mathcal{T}}^{\prime }$ the same length as $\mathcal{T}$ were available for each subject, the within-subject variance could also be estimated by taking the differences for each pair of subject-level measurements, $w_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)-w_{i,\mathcal{T}}\left(q,q^{\prime }\right)$, since

$$\begin{gathered} Va{r}_i\left\{w_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)-w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}=Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)-{\delta }_{i,\mathcal{T}}\left(q,q^{\prime }\right)-{\epsilon }_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\} \\ =2\text{Var}\left\{{\delta }_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}+2\text{Var}\left\{{\epsilon }_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\} \\ =2T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+2T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\} \\ =2{\sigma }_{\mathit{within}}^2\left(q,q^{\prime }\right). \end{gathered}$$

We call this the “oracle” estimate of within-subject variance. However, since such repeated measurements are often not available in practice, we propose the following estimation procedure for within-subject variance using single-session fMRI data.

Assume without loss of generality that T is even, and define the two sub-time series ${\mathcal{T}}_1=\left\{1,\dots ,\frac{T}{2}\right\}$ and ${\mathcal{T}}_2=\left\{\frac{T}{2}+1,T\right\}$.¹ Consider $w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)$ and $w_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)$, the estimates of static connectivity within each sub-time series. Applying the measurement error model in equation (1) we can write

$$\begin{gathered} w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)\text{and} \\ {w}_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right). \end{gathered}$$

Note that $w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)$ and $w_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)$ have μ_i(q, q′) in common, since it represents long-term average connectivity for subject i. We may assume that ${\delta }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)$ and ${\delta }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)$ (and ${\epsilon }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)$ and ${\epsilon }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)$) are approximately independent, as long as T/2 is large relative to the autocorrelation in the time series.² Note that since ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ have the same autocorrelation structure as $\mathcal{T}$, the autocorrelation time for ${\delta }_{i,{\mathcal{T}}_j}\left(q,q^{\prime }\right),j=1,2$, is also τ_δ. Hence, the ESS of ${\left\{{\delta }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in {\mathcal{T}}_j}$ is (T/2)/τ_δ = T_δ/2. Similarly, the autocorrelation time for ${\epsilon }_{i,{\mathcal{T}}_j}\left(q,q^{\prime }\right),j=1,2$, is τ_ε, and its ESS is T_ε/2. Therefore, for j = 1, 2,

$$\begin{gathered} {\delta }_{i,{\mathcal{T}}_j}\left(q,q^{\prime }\right)~N\left\{0,{\left(T_{\delta }/2\right)}^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right\}\text{and} \\ {\epsilon }_{i,{\mathcal{T}}_j}\left(q,q^{\prime }\right)~N\left\{0,{\left(T_{\epsilon }/2\right)}^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\}. \end{gathered}$$

Taking the difference $w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)$ for each subject, we can compute

$$\begin{gathered} Va{r}_i\left\{w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)\right\}=Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)-{\delta }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)-{\epsilon }_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)\right\} \\ =2Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)\right\}+2Va{r}_i\left\{{\epsilon }_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)\right\} \\ =4T_{\delta }^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+4T_{\epsilon }^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right) \\ =4{\sigma }_{\mathit{within}}^2\left(q,q^{\prime }\right). \end{gathered}$$

Therefore, ${\widehat{\sigma }}_{\mathit{within}}^2\left(q,q^{\prime }\right)=\frac{1}{4}Va{r}_i\left\{w_{i,{\mathcal{T}}_1}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_2}\left(q,q^{\prime }\right)\right\}$ serves as a single-session estimate of the within-subject variance of $w_{i,\mathcal{T}}\left(q,q^{\prime }\right)$. Using this, along with the estimate of total variance, $Va{r}_i\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}$, we can determine the optimal degree of shrinkage given in equation (2) for each connection.

2.2 Assessing reliability of biased estimators with ICC_MSE

To assess the benefits of shrinkage for enhancing reliability of FC estimates, we need a meaningful way to quantify and compare the accuracy of both traditional and shrinkage estimates. One measure commonly used to quantify reliability of a measure is the intra-class correlation coefficient (ICC). The ICC of an estimate is equal to the ratio of between-subject variance to total (between- plus within-subject) variance. Therefore, the optimal degree of shrinkage of an estimate is equal 1 – ICC of that estimate. This illustrates how the degree of shrinkage is related to the reliability, with very reliable estimates (ICC close to 1) receiving very little shrinkage towards the group mean, and very unreliable estimates (ICC close to 0) receiving almost complete shrinkage to the group mean.

While ICC is a popular measure of reliability due to its interpretability, it is not a meaningful measure of reliability for shrinkage estimates. This is because shrinkage trades bias for a reduction in variance to achieve an overall reduction in mean squared error (MSE), equal to variance plus squared bias. Therefore, only considering the variance of a shrinkage estimate provides an incomplete and overly optimistic picture of its accuracy. We propose a new measure of reliability for both biased and unbiased estimates, ICCmse, which replaces within-subject variance in the ICC formula with within-subject MSE. For unbiased estimates, including traditional estimates of FC with no shrinkage, ICC_MSE is the same as ICC, since MSE equals within-subject variance when bias is zero. However, for shrinkage estimates ICC_MSE considers both within-subject variance and squared bias to provide an overall picture of reliability, on the same scale as ICC. For the traditional and shrinkage estimates $w_{i,\mathcal{T}}\left(q,q^{\prime }\right)$ and ${\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)$, ICC_MSE is computed as

$$\begin{gathered} {\text{ICC}}_{\mathit{MSE}}\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}=\frac{{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}{{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)+\mathit{MSE}\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}} \\ {\text{ICC}}_{\mathit{MSE}}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}=\frac{{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}{{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)+\mathit{MSE}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}}, \end{gathered}$$

where we estimate MSE as the mean squared difference (MSD) across repeated estimates, divided by two since both sets of estimates are observed with noise. That is, letting ${\mathcal{T}}^{\prime }$ index a second fMRI session the same length as $\mathcal{T}$,

$$\begin{gathered} \mathit{MSE}\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right))\right\}=\frac{1}{2n}{\displaystyle \sum _{i=1}^n{\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)\right\}}^2,} \\ \mathit{MSE}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}=\frac{1}{2n}{\displaystyle \sum _{i=1}^n{\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}^{\prime }}\left(q,q^{\prime }\right)\right\}}^2.} \end{gathered}$$

Note that for both the traditional and shrinkage estimates, in the absence of the ground truth connectivity we use the traditional estimate from a second fMRI session to estimate MSE. In particular, we do not use shrinkage estimates from the second session to assess reliability of shrinkage estimates; this would artificially reduce MSE, since estimates from both sessions would be moved towards the group average, which is very stable across visits. Instead, using the traditional estimate from the second session in place of the truth allows the shrinkage and traditional estimates to be compared fairly.

If we wish to quantify the reliability of an entire seed connectivity map, the image intra-class correlation coefficient (I2C2) is often used instead of the ICC (Shou et al., 2013). Using the ICC_MSE framework, we can assess the accuracy of traditional and shrinkage estimates of connectivity maps and matrices using measures analogous to the I2C2. For seed q, let ${\mathbf{w}}_{i,\mathcal{T}}\left(q\right)$ and ${\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q\right)$ be the traditional and shrinkage estimates, respectively, of the true Q × 1 seed connectivity map μ_i(q). Then, the I2C2_MSE of each estimated image is computed as

$$\begin{gathered} {\text{I2C2}}_{\mathit{MSE}}\left\{{\mathbf{w}}_{i,\mathcal{T}}\left(q\right)\right\}=\frac{{\displaystyle {\sum }_{q^{\prime }\ne q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}{{\displaystyle {\sum }_{q^{\prime }\ne q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}+{\displaystyle {\sum }_{q^{\prime }\ne q}\mathit{MSE}\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}}}, \\ {\text{I2C2}}_{\mathit{MSE}}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q\right)\right\}=\frac{{\displaystyle {\sum }_{q^{\prime }\ne q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}{{\displaystyle {\sum }_{q^{\prime }\ne q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}+{\displaystyle {\sum }_{q^{\prime }\ne q}\mathit{MSE}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}}}. \end{gathered}$$

Similarly, letting ${\mathbf{W}}_{i,\mathcal{T}}$ and ${\stackrel{\sim }{W}}_{i,\mathcal{T}}$ be the traditional and shrinkage estimates, respectively, of the true Q × Q connectivity matrix M_i, the omnibus ICC_MSE (oICC_MSE) of each estimate is computed as

$$\begin{gathered} {\text{oICC}}_{\mathit{MSE}}\left\{{\mathbf{W}}_{i,\mathcal{T}}\right\}=\frac{{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}}{{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}+{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}\mathit{MSE}\left\{w_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}}}}, \\ {\text{oICC}}_{\mathit{MSE}}\left\{{\stackrel{\sim }{W}}_{i,\mathcal{T}}\right\}=\frac{{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}}{{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)}}+{\displaystyle {\sum }_q{\displaystyle {\sum }_{q^{\prime }>q}\mathit{MSE}\left\{{\stackrel{\sim }{w}}_{i,\mathcal{T}}\left(q,q^{\prime }\right)\right\}}}}. \end{gathered}$$

ICC_MSE, I2C2_MSE and omnibus ICC_MSE each range from 0 to 1, where 0 signifies no reliability and 1 indicates perfect reliability across repeated measurements from the same subject. They reduce to ICC, I2C2, and omnibus ICC, respectively, in the absence of bias, which is the case for traditional estimates.

3 Reliability study

We use test-retest data from the Human Connectome Project (Hep) to assess the reliability of traditional and shrinkage estimates of whole-brain FC between 100 regions identified using independent components analysis (ICA). Leveraging the relatively long duration of the resting-state fMRI data in the HCP, we also also examine how scan length affects the degree of shrinkage and the reliability of both traditional and shrinkage estimates of FC. We also consider and compare full Pearson correlation and partial correlation estimated using ridge regression.

3.1 Data and processing

The HCP (Van Essen et al., 2013) is a collection of neuroimaging and phenotypic information for over one thousand healthy adult subjects (http://humanconnectome.org). For the analyses described below, we used the following data from the 523 subjects included in the 2014 Human Connectome Project 500 Parcellation+Timeseries+Netmats (HCP500-PTN) release. All MRI data were acquired on a customized 3T Siemens connectome-Skyra 3T scanner, designed to achieve 100 mT/m gradient strength. For 461 subjects, a multi-band/multi-slice pulse sequence with an acceleration factor of eight (Moeller et al., 2010; Feinberg et al., 2010; Setsompop et al., 2012; Xu et al., 2012; Uğurbil et al., 2013) was used to acquire four roughly 15-minute rs-fMRI sessions, each consisting of 1200 volumes sampled every 0.72 seconds at 2 mm isotropic spatial resolution. The sessions were collected over two visits that occurred on separate days, with two runs collected at each visit. Across runs at each visit, phase encoding directions were alternated between right-to-left (RL) and left-to-right (LR) directions.

Spatial preprocessing was performed using the minimal preprocessing pipeline as described by Glasser et al. (2013), which includes correcting for spatial distortions and artifacts and projection of the data time series to the standard grayordinate space. Structured artifacts in the time series were removed using ICA + FIX (independent component analysis followed by FMRIB’s ICA-based X-noiseifier; Salimi-Khorshidi et al., 2014; Griffanti et al., 2014), and each data set was temporally demeaned with variance normalization according to Beckmann and Smith (2004). As part of the HCP500-PTN release, group independent component analysis (GICA) was performed on the full rs-fMRI time series for all 461 subjects to estimate a set of 100 spatial independent components (ICs) (Beckmann and Smith, 2004). Time courses were estimated for each subject and IC by performing the first stage of dual regression (Beckmann et al., 2009). Specifically, the group IC spatial maps were used as predictors in a multivariate linear regression model against the full rs-fMRI time series. To eliminate acquisition-related variability, we only used the IC time courses associated with the runs acquired with LR phase encoding, which corresponded to observations 1–1200 (visit 1) and 2401–3600 (visit 2) within the IC text file for each subject.³

We assigned each IC to one of seven resting-state networks (RSNs) based on overlap with the Allen parcellation, a publicly available set of 100 ICs that have been previously classified as resting state networks (RSNs) or noise by a group of experts (Allen et al., 2014). The 50 Allen ICs classified as RSNs are organized into seven large functional groups: default mode (DMN), cognitive-control (CC), visual (V), sensorimotor (SM), auditory (A), cerebellar (CB) and sub-cortical (SC) networks. As in Choe et al. (2017), we calculated the percent variance explained by the seven sets of Allen RSNs for each of the 100 HCP ICs to determine network membership. Several ICs were reassigned based on visual inspection of their spatial distributions and temporal spectra averaged across subjects, resulting in the final RSN assignments shown in Figure 1. Six HCP ICs were identified as likely representing nuisance signals; their time courses were regressed from the remaining 94 HCP signal ICs.

Figure 1.

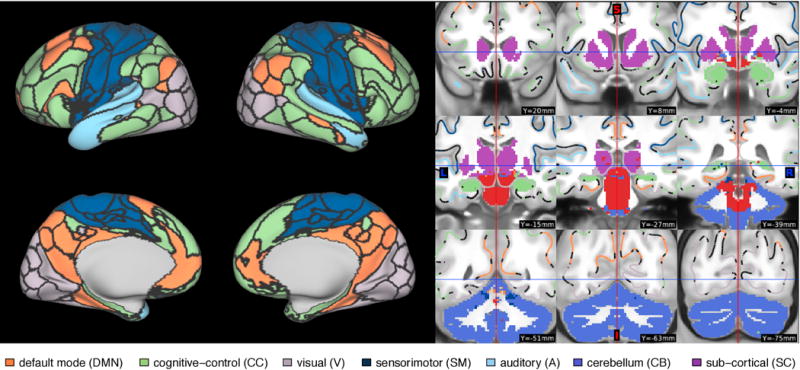
Resting-state network assignment of each IC based on overlap with the Allen parcellation. Cortical boundaries delineate the borders between ICs, based on a discretization of the continuous spatial ICA maps, used for visualization purposes. ICs labeled as noise are displayed in red.

3.2 Reliability analysis

The quantity of interest for each subject is the Q × Q matrix of pairwise FC between each of the Q = 94 signal ICs. We estimate the full correlation between each pair of ICs using Pearson correlation. We also estimate the partial correlation between each pair of ICs as described in the following section. Both measures are Fisher-transformed before performing shrinkage.

3.2.1 Partial correlation estimation

We estimate partial correlation using ridge regression as proposed by Ha and Sun (2014). Specifically, given a sample correlation matrix S (p × p), the partial correlation matrix using ridge regression is given by R = −scale{(S + ρI_p)⁻¹}, where scale(A) = diag(A)^−1/2Adiag(A)^−1/2 (Ha and Sun, 2014). Several heuristics have been proposed to choose the regularization parameter, ρ. For instance, the discrepancy principle tries to find the point at which the residual of the regularized solution is comprised only of noise but assumes that the standard deviation of the noise is known (Morozov, 1984). The L-curve criterion tries to balance regularization error and perturbation error by finding the L-shaped corner of the log-log plot of the regularized solution versus the norm of the corresponding residual vector (Hansen, 1992). Generalized cross-validation attempts to minimize the average prediction error or maximize the out-of-sample likelihood in group studies (Golub et al., 1979; Varoquaux et al., 2010; Varoquaux and Craddock, 2013). However, many functional connectivity studies employing ridge regression choose ρ in an ad-hoc fashion, with values ranging from 0.01 (e.g., Smith et al., 2015) to 1 or larger, and currently no consensus exists on the best choice or method of choosing ρ. Therefore, we first conduct a reliability analysis to assess the impact of the choice of ρ on the reliability of partial correlation estimates for varying scan duration.

For ρ = {0.01, 0.05, 0.1, 0.5, 1, 5, 10, 50, 100}, we estimate the partial correlation matrix for each subject using the first ℓ = {100, 200, …, 1200} volumes of both visits. For comparison, we also compute estimates of full correlation for each scan duration. We use the resulting set of repeated estimates to compute the omnibus intra-class correlation coefficient (oICC) of the partial and full correlation matrix estimates as an overall measure of their reliability. As with ICC, omnibus ICC ranges from 0 to 1, with 0 indicating that the estimates contain no subject-level information and 1 indicating that they are perfectly reliable across multiple observations of the same subject. Note that the choice of ρ changes the scale of partial correlation values, with larger ρ resulting in smaller partial correlations. Therefore, partial correlations obtained using different ρ values cannot be compared directly or with full correlations; however, ICC is scale-free and can be compared across measures on different scales. To assess the reliability of full and partial correlations for different types of connections, we also compute the average ICC across all within-network connections for each network shown in Figure 1.

Figure 2 displays the results of this reliability analysis. Figure 2a shows that, as expected, reliability increases with scan duration for each measure. More surprisingly, however, we observe that the reliability of partial correlation estimates using small values of ρ are much less reliable than full correlations; reliability increases with ρ up to ρ = 50, with ρ = 50 and ρ = 100 resulting in partial correlations with similar overall reliability to that of full correlations. Figure 2b shows that for highly reliable connections, e.g. those within the DMN and CC networks, partial correlations are more reliable than full correlations for p greater than 0.5, and reliability of these connections is maximized at ρ = 5. For other networks, partial correlations are generally less reliable than full correlations for smaller values of ρ and achieve similar reliability for larger values of ρ. Based on these findings, we use ρ = 5 to estimate partial correlations, as this choice maximizes the reliability of the most consistent connections and achieves somewhat comparable reliability to full correlations for all other within-network connections.

Figure 2.

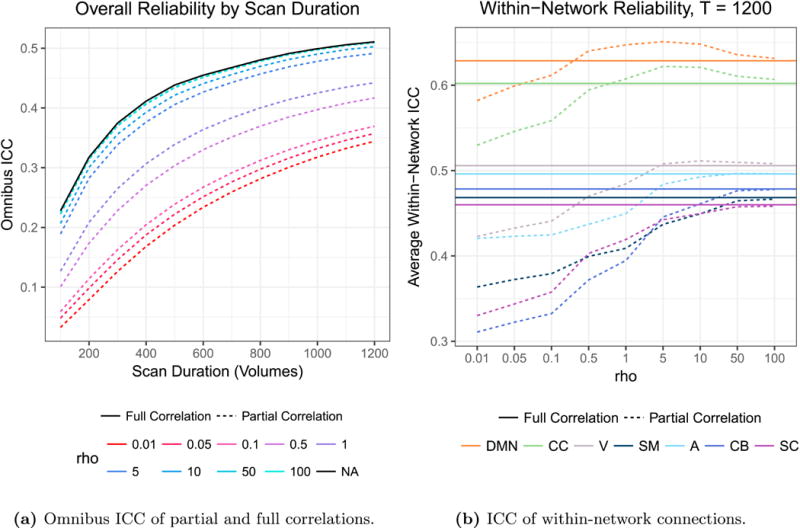
(a) As expected, reliability increases with scan duration for each measure. More surprisingly, we observe that the overall reliability of partial correlation estimates is much lower than that of full correlation estimates for small values of ρ, while large values of ρ (50 and 100, which are nearly indistinguishable in the plot) result in partial correlation estimates with comparable overall reliability to full correlation. Reliability begins to worsen slightly when ρ is increased from 50 to 100, suggesting that further increases in ρ would not result in improved reliability of partial correlations. (b) For connections within the DMN and CC networks, partial correlations are more reliable than full correlations for ρ greater than 0.5, and the maximal reliability is seen for partial correlations with ρ = 5. For all other networks, partial correlations are generally less reliable than full correlations for smaller values of ρ and achieve similar reliability for larger values of ρ.

3.2.2 Shrinkage estimation of functional connectivity

We use the first visit from each subject to compute traditional and shrinkage estimates of functional connectivity (full and partial correlation) based on varying scan length. We reserve the second visit to assess the accuracy of each of those estimates. Specifically, as described in Section 2.1 we compute traditional and shrinkage estimates of the FC matrix using the first ℓ = 100, 200, …, 1200 volumes of visit 1 for each subject. With a TR of 0.72 seconds, the resulting time series range in duration from 1.2 to 14.4 minutes. Using the second visit, we compute only the traditional estimate of the FC matrix using the full time series (1200 volumes) for each subject as an unbiased proxy for the ground truth. We also assess the performance of an “oracle” shrinkage estimator, which uses the oracle estimate of within-subject variance described at the beginning of Section 2.1.2. This provides an upper bound on the reliability of shrinkage estimators relative to the second visit, since it is based on the actual within-subject variance across the two visits.

For each scan duration, we assess the reliability of traditional, shrinkage and oracle estimates at multiple resolutions. First,/we compute ICC_MSE for each connection (q, q′), q′ ≠ q = 1, …, 100. Second, we compute I2C2_MSE for the seed connectivity map using each IC q = 1, …, 100 as the seed. Third, we compute the omnibus reliability of the connectivity matrix using oICC_MSE. Finally, we investigate reliability of traditional and shrinkage estimates of FC for connections within each resting-state network shown in Figure 1. For each network, we compute the average ICC_MSE of traditional and shrinkage estimates of FC across all within-network connections to determine the overall reliability of within-network connectivity at each scan duration.

3.3 Results

Throughout this section, we present the results using full correlations as the measure of FC in the upper triangle of each matrix and those using partial correlations (using ρ = 5) in the lower triangle.

Figure 3 displays the group-average connectivity matrix based on all 1200 volumes (approximately 15 minutes) of visit 1, which serves as the target for shrinkage of subject-level estimates based on the same scan duration. Figure 4 displays traditional and single-session shrinkage estimates of FC for three randomly selected subjects based on all 1200 volumes of visit 1, along with the “gold-standard” for each, the traditional estimate based on visit 2, which we use to assess reliability of the visit 1 estimates. The root MSE (rMSE) of each estimate, relative to visit 2, is displayed above the matrix. For all three subjects, the shrinkage estimate is closer to the observed connectivity at visit 2 (lower rMSE) than the traditional estimate. This improvement is seen for both full and partial correlations, although note that rMSE is not comparable across the two measures due to differences in scale.

Figure 3. Group-average FC.

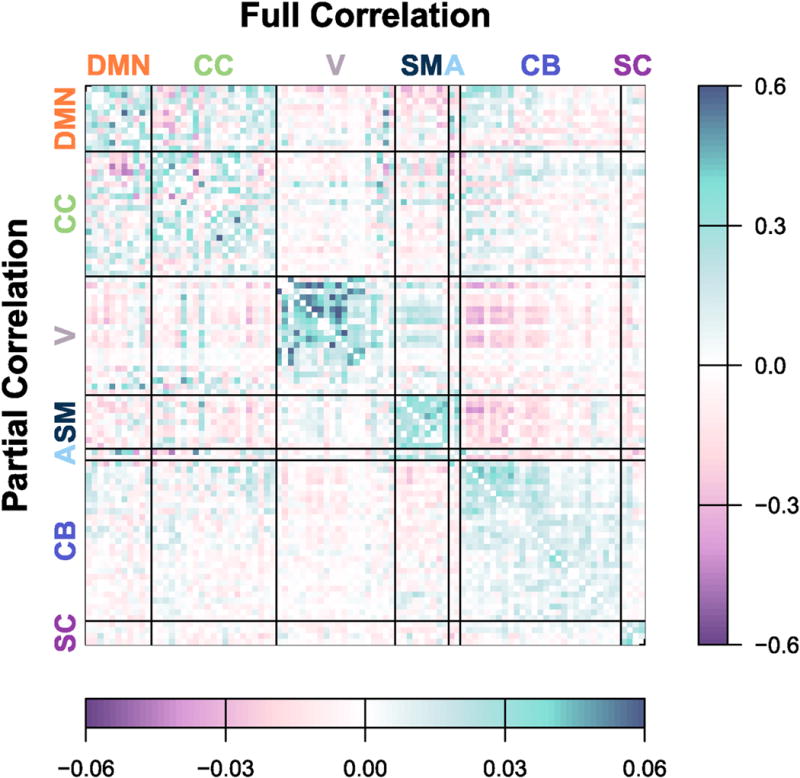
Average FC across all subjects, based on traditional estimates using all 1200 volumes of visit 1. Full correlations are displayed in the upper triangle; partial correlations are displayed in the lower triangle. Subject-level estimates based on the same scan duration are shrunk towards this group-level average to obtain more reliable estimates, where the degree of shrinkage for each connection depends on the within-subject and between-subject variance.

Figure 4. Subject-level estimates of FC.

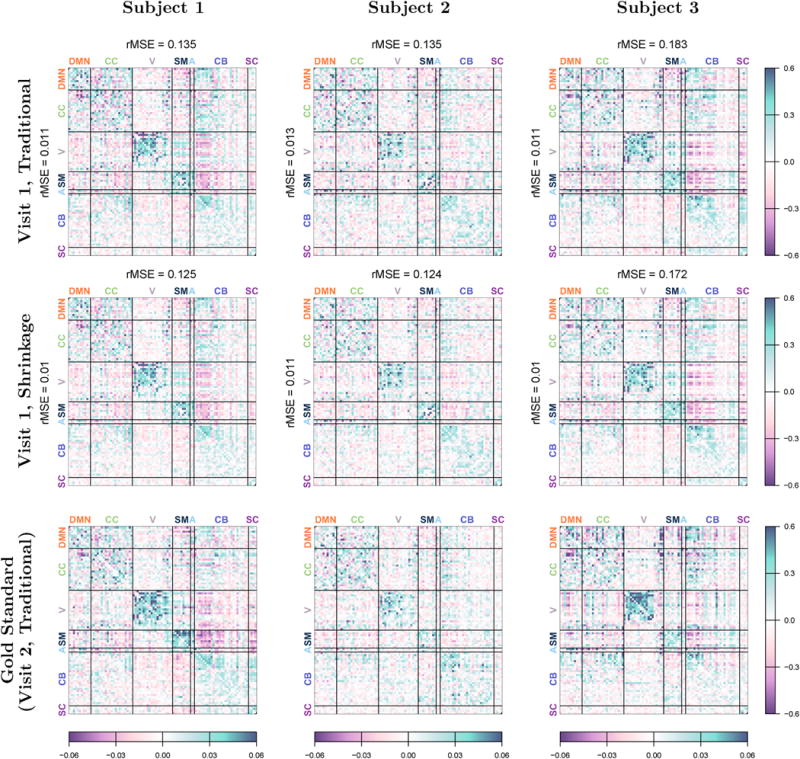
Traditional estimates (top row) and single-session shrinkage estimates (middle row) of subject-level FC based on all 1200 volumes of visit 1. Full correlations are displayed in the upper triangle of each matrix; partial correlations are displayed in the lower triangle. The bottom row shows FC for each subject at visit 2, based on the traditional estimate using all 1200 volumes. This estimate is used as a proxy for the truth to assess the accuracy of the visit 1 estimates. The root mean squared error (rMSE) of full and partial correlations, relative to visit 2, are displayed in the margins of each matrix.

Figure 4 also illustrates how the unique features of each subject are not lost through shrinkage. The shrinkage estimates are qualitatively similar to the traditional estimates for each subject, and many similar features are seen in both. For example, subject 1 displays strong anticorrelations between some cerebellar regions and the visual, sensorimotor and auditory networks, features that are preserved after shrinkage and replicated at visit 2. Subject 3 displays unusually strong negative partial correlations between some DMN and CC regions, features that are again preserved after shrinkage and reliable across both visits. This illustrates how, rather than discarding true subject-level information, shrinkage serves to reduce noise by bringing unreliable, noisy features closer to the group average, while retaining features that are observed to be reliable at the subject level.

Figure 5 displays the degree of shrinkage towards the group mean for single-session and oracle shrinkage for three different scan durations: 400, 800 and 1200 volumes, corresponding to approximately 5, 10 and 15 minutes, respectively. For each scan duration and shrinkage type, the degree of shrinkage for each unique pair of nodes is displayed. Figure 5a shows that the degree of shrinkage tends to decrease as scan duration increases, as traditional estimates of connectivity become more reliable and less shrinkage is required. The degree of shrinkage varies dramatically across the connectivity matrix, with more reliable connections (e.g., most within-network connections) receiving relatively little shrinkage and less reliable connections (e.g., those between the visual network and other networks) receiving more shrinkage. These patterns are somewhat similar whether full or partial correlation is used as the measure of FC, with some exceptions. For example, most connections involving cerebellar or subcortical regions receive more shrinkage using partial correlation, indicating that these connections are less reliable based on partial correlation. Meanwhile, some connections within and between the DMN and cognitive control networks receive slightly less shrinkage when partial correlation is used, indicating that these connections can be more reliably measured using partial correlation, with the caveat that ρ must be chosen correctly (see Figure 2).

Figure 5. Degree of shrinkage.

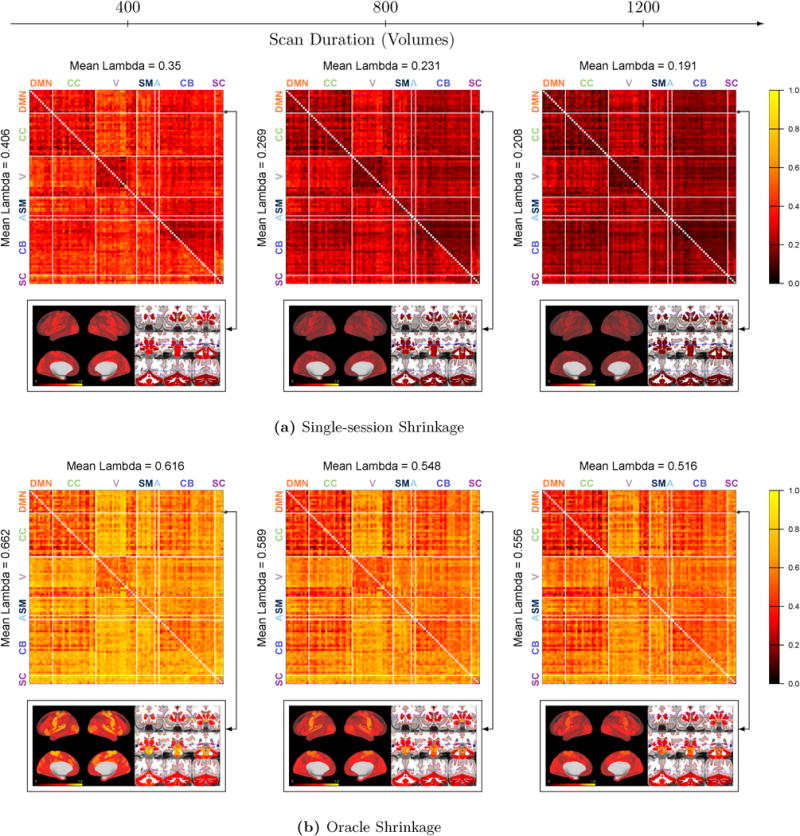
Each matrix shows the degree of shrinkage λ(q, q′) ∈ [0, 1] for the FC between nodes q and q′, based on single-session shrinkage(a) and oracle shrinkage (b). The upper triangle corresponds to full correlations and the lower triangle to partial correlations using ρ = 5. For one selected seed in the DMN (shown in black in the images), the degree of shrinkage for all connections with this seed is displayed as an image below the matrix, based on full correlations. Overall, the degree of shrinkage decreases as scan length increases; some connections receive more shrinkage than others due to differences in reliability; full and partial correlations show somewhat similar patterns of shrinkage with some notable differences; and single-session shrinkage tends to be more conservative (less shrinkage) than oracle shrinkage.

Below each matrix, we “zoom in” on all connections with one DMN seed region to better visualize the spatial differences in the degree of shrinkage for full correlations. The selected seed shown in black in each image. For this seed, the degree of shrinkage is highest for connections with motor, visual and auditory regions and is lowest with other default mode regions and cognitive control regions. This is consistent with previous findings that connectivity within and between the default mode and cognitive control networks tends to be highly reliable, while connectivity between the DMN and other networks is generally less reliable (Van Dijk et al., 2010; Finn et al., 2015; Laumann et al., 2015; Airan et al., 2016).

Figure 5b shows that oracle shrinkage results in substantially greater shrinkage compared with single-session shrinkage. Recall that single-session shrinkage is based on an estimate of within-subject variance from a single session, while oracle shrinkage is based on within-subject variance across multiple sessions, in this case occurring on separate days. The greater degree of shrinkage with oracle shrinkage is reflective of greater within-subject variance in FC across sessions than within a single session. This is not surprising, since inter-session differences in FC and related measures have been found to be greater than intra-session differences (Shehzad et al., 2009; Anderson et al., 2011; Birn et al., 2013; Zuo et al., 2013). Single-session shrinkage can therefore be considered a conservative form of shrinkage, since it tends to preserve more subject-level information than oracle shrinkage. However, the patterns of shrinkage within the connectivity matrix are similar for oracle and single-session shrinkage, suggesting that the proposed single-session within-subject variance estimator is an attenuated version of the true within-subject variance across multiple sessions.

Figure 6 displays the reliability of traditional, single-session shrinkage and oracle shrinkage estimates of connectivity by scan duration. The upper triangle of each matrix shows the ICC_MSE of full correlations; the lower triangle shows that of partial correlations. For each measure, the I2C2_MSE of each node and the omnibus ICC_MSE are displayed in the margins of the upper and lower triangles. As previously observed in terms of degree of shrinkage, Figure 6a shows that reliability tends to increase with scan duration and the most reliable connections are those within and between the DMN and cognitive control networks. Connections between these networks and some visual and cerebellar nodes are also among the most reliable.

Figure 6. Reliability of FC estimates.

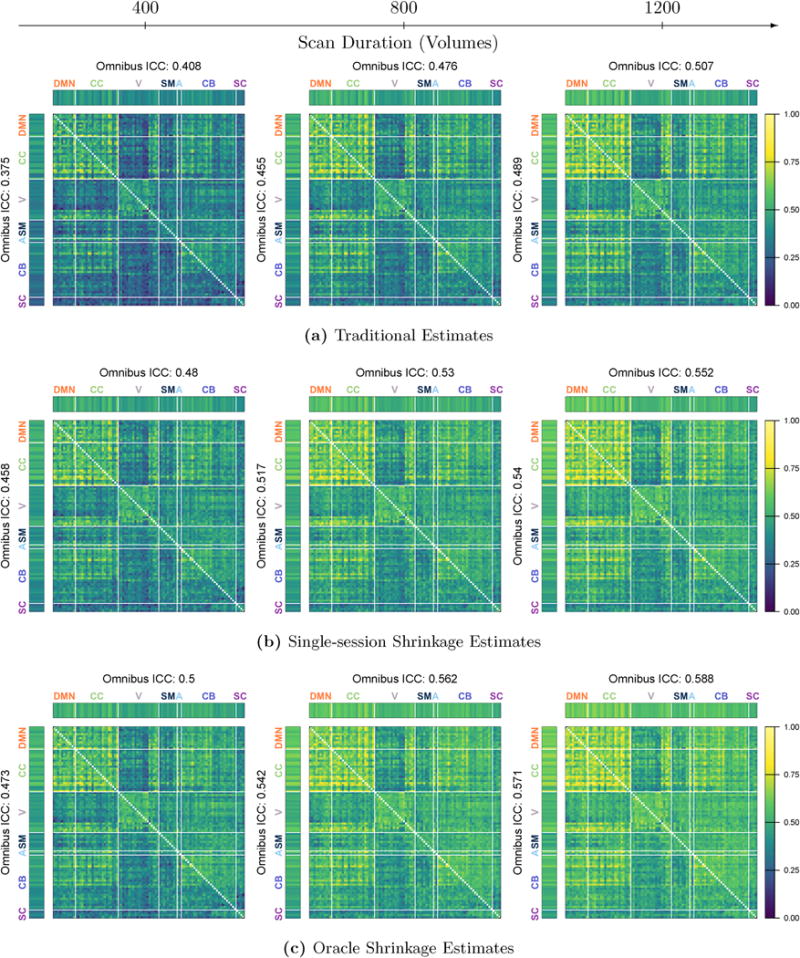
For each estimation method and scan duration, the ICC_MSE of all unique region-pairs is displayed for full correlations in the upper triangle and for partial correlations in the lower triangle; I2C2_MSE for each region and omnibus ICC_MSE are displayed in the margins for each measure.

Figure 6b shows that single-session shrinkage estimates are significantly more reliable than traditional estimates of connectivity at each scan duration, with improvement observed across all parts of the connectivity matrix. Not surprisingly, the benefits of shrinkage are greatest for shorter scan duration, but improvement is still substantial for 1200-volume (approximately 15-minute) acquisitions. Specifically, based on full correlations, single-session shrinkage increases omnibus ICC_MSE by 17.6% for 400-volume scans, 11.3% for 800-volume scans, and 8.9% for 1200-volume scans; based on partial correlations, the improvement is slightly higher at 22.1%, 13.6% and 10.4%, respectively. Notably, single-session shrinkage estimates based on 5-minute (400-volume) acquisitions are nearly as reliable as traditional estimates based on 15-minute (1200-volume) acquisitions.

Figure 6c displays the reliability of oracle shrinkage estimates. Oracle shrinkage provides an upper bound on the benefit of shrinkage, since it uses the same repeat measurements used to assess reliability to determine the optimal degree of shrinkage. While oracle shrinkage estimates are more reliable than single-session shrinkage estimates, the improvement is less dramatic than that of single-session shrinkage estimates over traditional estimates. For example, based on full correlations oracle shrinkage increases omnibus ICC_MSE over single-session shrinkage by an additional 4.2% with 400 volumes and 6.5% with 1200 volumes. However, as seen in Figure 5, on average oracle shrinkage requires nearly twice the amount of shrinkage toward the group mean; single-session shrinkage therefore achieves much of the possible improvements in reliability, while preserving more subject-level information than oracle shrinkage.

Figure 7 displays the average reliability of all within-network connections for the seven resting-state networks shown in Figure 1. For traditional and shrinkage estimates alike, connections within the default mode and cognitive control networks are by far the most reliable in terms of ICC_MSE, while connections within the visual, sensorimotor, auditory, cerebellar and subcortical networks tend to be less reliable. Due to the choice of ρ = 5 (see Figure 2), partial correlations are more reliable than full correlations for connections within the DMN and cognitive control networks and are worse than or comparable to full correlations for all other networks.

Figure 7. Accuracy of within-network FC estimates.

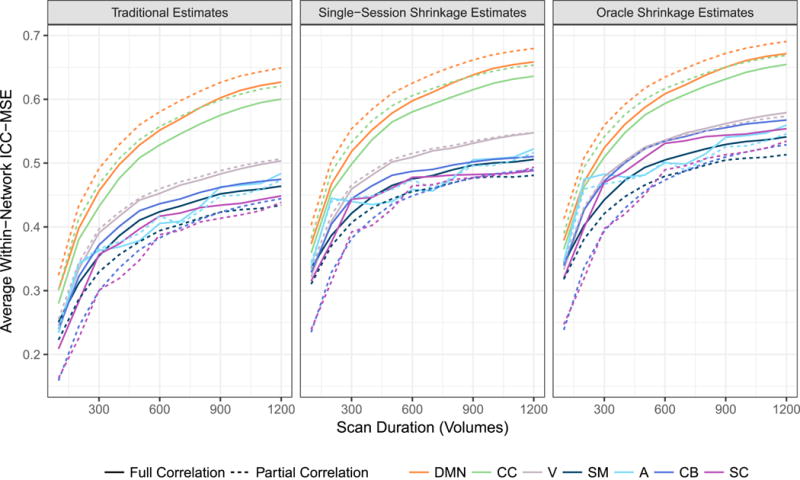
Average ICC_MSE across all within-network connections within each network for traditional and single-session shrinkage estimates of FC. For both types of estimates, accuracy tends to taper off with increasing scan duration, but shrinkage estimates are substantially more accurate than traditional estimates across all durations.

For both full and partial correlations, single-session shrinkage estimates of within-network FC are sub-stantially more reliable than traditional estimates across all scan durations and networks. The improvement is most dramatic for shorter durations, with an increase in ICC_MSE of 24.0 – 50.9% across the different networks using full correlation and 24.3 – 47.7% using partial correlation, based on 100-volume acquisitions. Based on 1200-volume acquisitions, the improvement is 5.1 – 9.0% using full correlation and 4.7 – 12.6% using partial correlation. Note that even the most reliable connections based on the longest scan durations become more reliable with shrinkage. For example, based on 1200-volume acquisitions, the ICC_MSE of partial correlations within the DMN increases from 0.649 to 0.680 (4.7%) due to shrinkage, and within the CC network from 0.621 to 0.654 (5.3%). This suggests that reliability of certain connections can be maximized by simultaneously increasing scan duration, employing partial correlations—if ρ can be chosen optimally—and performing shrinkage on the resulting estimates.

4 Discussion

In this paper, we propose an empirical Bayes shrinkage method for resting-state functional connectivity (FC) using single-session fMRI data. The proposed method is rooted in a novel measurement error model for FC that takes into account between-subject differences in FC, sampling error in estimation of FC, and dynamic changes in FC over time. In contrast with previously proposed Bayesian or shrinkage methods for FC, this method does not require access to multiple fMRI sessions. To compare the reliability of shrinkage and traditional estimates in a scale-free way, we also propose a novel reliability measure, ICC_MSE, applicable to both biased and unbiased estimators. The ICC_MSE reduces to the intra-class correlation coefficient (ICC) in the absence of bias. Similar to ICC, it ranges from 0 to 1, and is a measure of how much reliable subject-level information is contained in a set of estimates, relative to the variance across subjects. As with ICC, ICC_MSE can also be used to compare reliability of estimates on different scales, such as full and partial correlations. Finally, we illustrate a multi-resolution approach to evaluate reliability of FC at the level of individual connections, seed maps, networks, and the entire entire connectivity matrix. This approach can be used to assess the effects of shrinkage, scan duration, connectivity measure and other factors on overall reliability of FC and how these effects vary across different networks, regions and connections.

We test the proposed methods on 461 subjects from the Human Connectome Project, using both full and partial correlation as the measure of FC. We find that single-session shrinkage improves overall reliability of FC estimates by approximately 18 – 22% for 5-minute (400-volume) acquisitions and 9 – 10% for 15-minute (1200-volume) acquisitions. As consistently observed in the literature, we find that reliability varies substantially across connections, with the most reliable connections being those within and between the default mode and cognitive control networks, and between those networks and certain visual and cerebellar regions. Notably, we find that shrinkage substantially improves even the most reliable connections based on the longest acquisitions.

Both full and partial correlations benefit from shrinkage to similar degrees. However, we find that the choice of ρ is critical for partial correlations, and that partial correlations are generally less reliable overall than full correlations, particularly for small values of ρ. This is consistent with the findings of Abraham et al. (2017), whose analysis was based on the Autism Brain Imaging Data Exchange (ABIDE) dataset (Di Martino et al., 2014); compared to the HCP, the resting-state fMRI data of ABIDE are of shorter duration, have longer TR, and are based on less sophisticated acquisition and processing techniques. Therefore, our results serve to somewhat generalize these previous findings. However, we also find that certain connections actually become more reliable using partial correlations for specific values of ρ, as illustrated in Figure 2b. This likely reflects the property that partial correlations are used to estimate a relative few “direct” connections, while shrinking the remaining “indirect” connections towards zero. These indirect connections may be meaningfully estimated when using full correlation but are essentially equal to zero for all subjects using partial correlations, hence resulting in worse reliability as measured by ICC. This illustrates the importance of investigating reliability at multiple resolutions and focusing on connections of interest when assessing the value of various processing and analysis choices or determining optimal parameter values.

If “direct” connections are of primary interest, the use of partial correlation combined with a principled method for choosing ρ may thus be beneficial. While we find ρ = 5 to maximize the reliability of certain connections, the optimal value likely depends on many factors specific to the dataset being analyzed, along with the particular connections of interest. Therefore, ρ should be chosen for each analysis in a principled manner. For example, ρ can be chosen to maximize reliability using a measure (e.g., ICC) that (1) is scale-free and therefore robust to changes in scale of partial correlations induced by changes in ρ, and (2) reflects within-subject reliability relative to differences between subjects. We did not find that scan duration strongly influenced the choice of ρ to maximize overall reliability, so it seems reasonable to use intra-session reliability as a proxy for inter-session reliability in the absence of retest data. Overall, our results suggest that future research is needed to develop principled methods for estimating partial correlations in order to fully realize their benefits.

We also perform “oracle” shrinkage to provide an upper limit on the inter-session reliability that can be achieved with shrinkage. We find that oracle shrinkage results in approximately double the degree of shrinkage towards the group average versus single-session shrinkage, as seen in Figure 5. This is due to higher inter-session variance of FC, the basis of oracle shrinkage, compared with intra-session variance, the basis of single-session shrinkage. Single-session shrinkage is therefore a conservative form of shrinkage for FC, as it places greater weight on the original subject-level estimates compared with oracle shrinkage; yet it captures most of the possible improvement in inter-session reliability, suggesting that the proposed single-session shrinkage methods offer significant benefits while preserving subject-level information.

While in this paper we focus on static connectivity, the proposed methods are directly applicable to shrinkage of dynamic connectivity states shared across subjects. For each state, the proposed model is simply applied to the time series for each subject corresponding to that state (these are allowed to differ in duration across subjects, with subject-specific variance estimators given in Appendix A). Performing shrinkage within each state is indeed likely beneficial, since within each state variation in true connectivity is reduced, and therefore shrinkage will be driven more by random noise than dynamic fluctuations, which are biologically meaningful and potentially of interest. In the complete absence of dynamic fluctuations, within-subject variance of FC would reflect primarily differences in SNR across the brain as well as motion and physiological confounds. These latter sources of variation, if measured, can also be removed from the data before performing shrinkage, which would serve to reduce the total noise and lead to less shrinkage of subject-level estimates of FC. Indeed, any processing steps that serve to reduce noise at the subject level are highly advisable prior to shrinkage in order to maximize the SNR in the estimates and therefore minimize shrinkage. In this way, shrinkage can also be used as a way to assess the benefit of various processing and analysis choices in the absence of retest data, with choices leading to minimal shrinkage being most beneficial.

Here we have focused on reliability across multiple visits, but it is important to consider the measure or effect of interest when choosing how to assess reliability. While reliability across multiple visits is appropriate for detecting trait-level effects, which are stable over long periods of time, reliability within a single visit is more appropriate for state-level effects. Functional connectivity is known to vary substantially across visits, so single-session estimates of FC will tend to achieve only modest inter-session reliability, limiting their utility for studying trait-level effects. Several recent studies have suggested that it may be preferable to combine data from multiple sessions occurring on different days, rather than simply increase scan duration within a single session (Shehzad et al., 2009; Laumann et al., 2015; Noble et al., 2017b).

In this study we assess the reliability of FC estimates produced from scans up to approximately 15 minutes in duration. Even within this relatively short scan duration, the results shown in Figure 7 suggest that increasing scan duration, while beneficial, offers diminishing returns in terms of improving inter-session reliability. Reliability of FC has been shown to depend on many factors, including the connection(s) of interest, temporal and spatial resolution, node definition, and the measure of functional connectivity, as well as how reliability is defined (Zuo et al., 2013; Murphy et al., 2007; Anderson et al., 2011; Smith et al., 2011; Dawson et al., 2013; Birn et al., 2013; Zuo et al., 2013; Liao et al., 2013; Airan et al., 2016). In light of this, it is not surprising that recommendations regarding how long to scan have differed widely, ranging from 7 minutes or less (Tomasi et al., 2016; Airan et al., 2016) to 90 minutes or more (Laumann et al., 2015). Our findings contribute to a growing body of work that suggests that maximizing reliability requires not only increasing the duration or number of scans, but adopting other best practices in processing and analysis, such as borrowing strength across subjects through shrinkage.

Our study has several limitations. Our results are based on a single dataset, parcellation, and subject group; while we believe that the findings are generalizable, future work should focus on determining the effect of shrinkage in different contexts. Additionally, while we perform connection-specific shrinkage, we apply the same degree of shrinkage to each subject. It is plausible that reliability of FC differs based on subject characteristics, and therefore differential shrinkage across subjects would be more beneficial. While tailoring the degree of shrinkage for different subjects is possible, doing so increases the number of parameters that must be estimated and may therefore actually worsen the performance of shrinkage estimators (Mejia et al., 2015). This should be explored as an area of future research.

A Differing scan duration

In some studies, subjects may have varying scan duration, due to differences in protocol, varying ability of subjects to undergo scanning, or scrubbing (removal of volumes contaminated with artifacts) during preprocessing. Let ${\mathcal{T}}_i=\left\{1,\dots ,T_i\right\}$ index the fMRI time series for subject i. Then, the model in equation (1) becomes

$$w_{i,\mathcal{T}}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right),$$

and ${\delta }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)$ and ${\epsilon }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)$ are approximately distributed

$$\begin{gathered} {\delta }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)=\frac{1}{T_i}{\displaystyle \sum _{t=1}^{T_i}{\delta }_{i,t}\left(q,q^{\prime }\right)~N\left\{0,T_{\delta ,i}^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right\}\text{and}} \\ {\epsilon }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)=\frac{1}{T_i}{\displaystyle \sum _{t=1}^{T_i}{\epsilon }_{i,t}\left(q,q^{\prime }\right)~N\left\{0,T_{\epsilon ,i}^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\}}, \end{gathered}$$

where T_δ,i = T_i/τ_δ and T_ε,i = T_i/τ_ε are the the effective sample size (ESS) of ${\left\{{\delta }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in {\mathcal{T}}_i}$ and ${\left\{{\epsilon }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in {\mathcal{T}}_i}$, respectively.

Then, the variance estimation procedures described in Section 2.1.2 can be modified as follows. First, note that the between-subject variance of the long-term average FC for each subject, ${\sigma }_{\mu }^2\left(q,q^{\prime }\right)$, is unchanged, but the total variance of the estimates $w_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)$ will vary across subjects due to differences in within-subject variance. Specifically, the within-subject variance for each subject is

$$\begin{gathered} {\sigma }_{\mathit{within},i}^2=T_{\delta ,i}^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+T_{\epsilon ,i}^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right) \\ ={\tau }_{\delta }{T}_i^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+{\tau }_{\epsilon }{T}_i^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right) \\ =T_i^{-1}\left\{{\tau }_{\delta }{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+{\tau }_{\epsilon }{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\} \\ =:T_i^{-1}c\left(q,q^{\prime }\right) \end{gathered}$$

and the common term c(q, q) can be estimated as follows. Assuming without loss of generality that T is even, define the two sub-time series ${\mathcal{T}}_{i,1}=\left\{1,\dots ,\frac{T_i}{2}\right\}$ and ${\mathcal{T}}_{i,2}=\left\{\frac{T_i}{2}+1,T_i\right\}$. For j = 1, 2, let $w_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)$ be the estimate of static connectivity within sub-time series ${\mathcal{T}}_j$ for subject i. As before, we can write $w_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)={\mu }_i\left(q,q^{\prime }\right)+{\delta }_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)$ for j = 1, 2, where the ESS of ${\left\{{\delta }_{i,t}\left(q,q^{\prime }\right)\right\}}_{t\in {\mathcal{T}}_{i,j}}$ is (T_i/2)/τ_δ and the ESS of ${\epsilon }_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)$ is (T_i/2)/τ_ε. Therefore, ${\delta }_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)~N\left\{0,2{\tau }_{\delta }{T}_i^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right\}$ and ${\epsilon }_{i,{\mathcal{T}}_{i,j}}\left(q,q^{\prime }\right)~N\left\{0,2{\tau }_{\epsilon }{T}_i^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right\}$ for j = 1, 2.

Taking the difference $w_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)$ for each subject, we can compute

$$\begin{gathered} Va{r}_i\left\{w_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)\right\}=Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)+{\epsilon }_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)-{\delta }_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)-{\epsilon }_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)\right\} \\ =2Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)\right\}+2Va{r}_i\left\{{\epsilon }_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)\right\} \\ =2E\left[{\delta }_{i,{\mathcal{T}}_{i,1}}^2\left(q,q^{\prime }\right)\right]+2E\left[{\epsilon }_{i,{\mathcal{T}}_{i,1}}^2\left(q,q^{\prime }\right)\right] \\ =2E_{T_i}E\left[{\delta }_{i,{\mathcal{T}}_{i,1}}^2\left(q,q^{\prime }\right)|T_i\right]+2E_{T_i}E\left[{\epsilon }_{i,{\mathcal{T}}_{i,1}}^2\left(q,q^{\prime }\right)|T_i\right] \\ =2E\left[2{\tau }_{\delta }{T}_i^{-1}{\sigma }_{\delta }^2\left(q,q^{\prime }\right)\right]+2E\left[2{\tau }_{\epsilon }{T}_i^{-1}{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right] \\ =4\left({\tau }_{\delta }{\sigma }_{\delta }^2\left(q,q^{\prime }\right)+{\tau }_{\epsilon }{\sigma }_{\epsilon }^2\left(q,q^{\prime }\right)\right)E\left[T_i^{-1}\right] \\ =4c\left(q,q^{\prime }\right)E\left[T_i^{-1}\right] \end{gathered}$$

Therefore, c(q, q′) can be estimated as $\widehat{c}\left(q,q^{\prime }\right)=\frac{1}{4}{\left(\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{T}_i^{-1}}\right)}^{-1}Va{r}_i\left\{w_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)\right\}$, and the within-subject variance for subject i is estimated as ${\widehat{\sigma }}_{\mathit{within},i}^2=T_i^{-1}\widehat{c}\left(q,q^{\prime }\right)$.

The between-subject variance ${\sigma }_{\mu }^2\left(q,q^{\prime }\right)$ can be easily estimated as follows. Writing the total variance, which can be estimated directly from the data, as $Va{r}_i\left\{w_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)\right\}={\sigma }_{\mu }^2\left(q,q^{\prime }\right)+Va{r}_i\left\{{\delta }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)\right\}+Va{r}_i\left\{{\epsilon }_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)\right\}$, the between-subject variance estimate is ${\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)=Va{r}_i\left\{w_{i,{\mathcal{T}}_i}\left(q,q^{\prime }\right)\right\}-\frac{1}{2}Va{r}_i\left\{w_{i,{\mathcal{T}}_{i,1}}\left(q,q^{\prime }\right)-w_{i,{\mathcal{T}}_{i,2}}\left(q,q^{\prime }\right)\right\}$.

The degree of shrinkage for subject i is given by ${\lambda }_i\left(q,q^{\prime }\right)={\widehat{\sigma }}_{\mathit{within},i}^2\left(q,q^{\prime }\right)/\left({\widehat{\sigma }}_{\mathit{within},i}^2\left(q,q^{\prime }\right)+{\widehat{\sigma }}_{\mu }^2\left(q,q^{\prime }\right)\right)$. Subjects with longer scans will receive less shrinkage for a given connection than subjects with shorter scans, since their estimates are based on more data and are therefore more reliable.