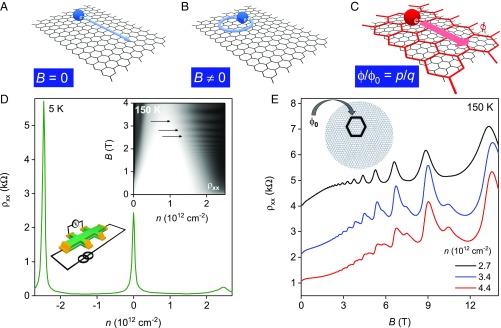
Fig. 1.

BZ oscillations in graphene/hBN superlattices. (A–C) Schematic illustration of electron trajectories for different magnetic fields. The blue spheres (A and B) are electrons propagating along trajectories indicated in blue. Graphene’s crystal lattice is shown as gray hexagons. The red sphere (C) represents a quasiparticle (magnetic Bloch state) propagating along a straight trajectory on a lattice of supercells (red hexagons), as if in zero effective magnetic field. Note however that in the presence of an electric field, trajectories in C may become curved and develop into chiral edge states because of nontrivial topology of the magnetic minibands (33–35, 39). (D) ρ_xx(n) for a graphene superlattice with the period of ∼14 nm. (Inset) Map ρ_xx(n,B) for electron doping. Logarithmic gray scale: white 80 Ω; black 1,200 Ω. (Lower Inset) Device and measurement schematics. (E) ρ_xx (B) at 150 K for three carrier densities above n₀. (Inset) Illustration of a graphene/hBN moiré superlattice. For n = 2.7 × 10¹² cm⁻², the oscillations exhibit a single periodicity, which corresponds to one ϕ₀ piercing the moiré unit cell (outlined by the black hexagon).