Abstract
Calorimetric studies of protein-ligand binding sometimes yield thermodynamic data that are difficult to understand. Today, molecular simulations can be used to seek insight into such calorimetric puzzles, and, when simulations and experiments diverge, the results can usefully motivate further improvements in computational methods. Here, we apply near-millisecond duration simulations to estimate the relative binding enthalpies of four peptidic ligands with the Grb2 SH2 domain. The ligands fall into matched pairs, where one member of each pair has an added bond that preorganizes the ligand for binding and thus may be expected to favor binding entropically, due to a smaller loss in configurational entropy. Calorimetric studies have shown that the constrained ligands do in fact bind the SH2 domain more tightly than the flexible ones, but, paradoxically, the improvement in affinity for the constrained ligands is enthalpic, rather than entropic. The present enthalpy calculations yield the opposite trend, as they suggest that the flexible ligands bind more exothermically. Additionally, the small relative binding enthalpies are found to be balances of large differences in the energies of structural components such as ligand and the binding site residues. As a consequence, the deviations from experiment in the relative binding enthalpies represent small differences between these large numbers and hence may be particularly susceptible to error, due, for example, to approximations in the force field. We also computed first-order estimates of changes in configurational entropy on binding. These too are, arguably, paradoxical, as they tend to favor binding of the flexible ligands. The paradox is explained in part by the fact that the more rigid constrained ligands reduce the entropy of binding site residues more than their flexible analogs do, at least in the simulations. This result offers a rather general counterargument to the expectation that preorganized ligands should be associated with more favorable binding entropies, other things being equal.
I. INTRODUCTION
Calorimetric studies of protein-small molecule interactions decompose the standard free energy of binding into the binding enthalpy and entropy—the so-called thermodynamic signature of binding.1–4 These components of the free energy may provide insight into the forces driving binding.5–7 It has also been argued that one should aim to design ligands whose binding is enthalpy-driven, as these may be better drugs than ones whose binding is entropy-driven.8,9 On the other hand, small changes in the chemical structure of a ligand often produce large changes in the binding enthalpy and entropy that are difficult to rationalize.10 Of particular interest here, several meticulous experimental studies have compared the binding of flexible versus extremely similar but preorganized ligands to small proteins. A more preorganized ligand may be expected to bind with higher affinity, all other things being equal, due to a reduced configurational entropy penalty on binding; but calorimetric studies have often shown a greater entropy penalty for constrained ligands.11–13
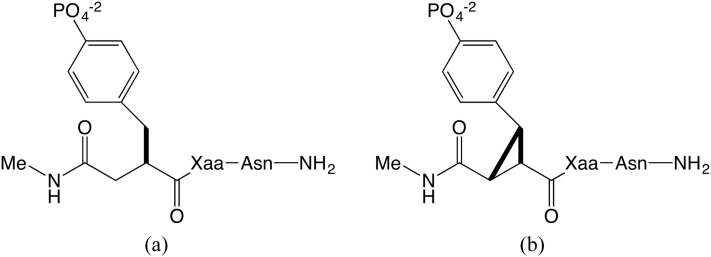
One elegant experimental study examined the binding thermodynamics of constrained and flexible phosphopeptides with the SH2 domain of growth factor receptor protein 2 (Grb2).14 The ligands in this case are amide-capped pseudopeptides which contain a varied central amino acid (X) flanked by a phosphotyrosine (pY) and an asparagine (N) (Fig. 1). For each flexible ligand [fpYXN, Fig. 1(a)], a constrained analog [cpYXN, Fig. 1(b)] was synthesized and tested under identical experimental conditions. The cpYXN ligands are conformationally constrained by cyclization of the phosphotyrosine to form a cyclopropane ring. As perhaps expected, the more rigid, and hence better preorganized, constrained peptides bind the protein with higher affinity.11 However, their greater affinity traces to a more favorable binding enthalpy, instead of the entropic advantage anticipated due to their preorganization.11
FIG. 1.
Flexible (a) and constrained (b) ligand structures, fpYXN and cpYXN, respectively, where Xaa (X) is either valine (V) or glutamine (Q). In accordance with the experimental study, both the N- and C-termini are capped with electrically neutral amide groups.
In recent years, advances in molecular simulations have opened new possibilities to study drug-protein binding in atomistic detail.15–20 In particular, although the binding enthalpy can be challenging to compute, with increasing computer power, it is increasingly practical to employ a straightforward direct approach to this calculation, which has been shown to yield numerically precise (though not necessarily accurate) results for host-guest systems.21–25 The direct approach is appealing for its simplicity, as well as its ability to provide a breakdown of enthalpy contributions from various components of the system, such as the ligand and the binding site residues.
Here, we use the direct method to estimate the relative binding enthalpies of two matched pairs of the Grb2 ligands discussed above, where each pair contains the same central residue, either valine (V) or glutamine (Q). With the multiple-graphical processor unit (GPU) version of AMBER PMEMD26 and long (4 fs) time steps made possible by hydrogen mass repartitioning,27 we achieved up to 450 ns of simulation per day and generated over 250 μs cumulative simulation time for each bound system. The results extend prior work28 which used many short simulations summing to 0.4 μs per system to compute relative binding enthalpy calculations for one constrained peptide and one matched flexible phosphopeptide binding to the Src SH2 domain. We furthermore examine how the ligand constraints affect changes in configurational entropy, of both the ligand and binding-site residues, on binding. The results are informative about the physics of molecular recognition and the methodology of computing binding enthalpies.
II. METHODS
A. Calculation of relative binding enthalpies
Relative binding enthalpies (ΔΔH) were estimated by the direct method21,28,22 which involves taking differences in mean (Boltzmann-averaged) potential energies for simulated systems of interest. With the direct method, the absolute protein-ligand binding enthalpy can be computed by running separate simulations of the ligand in solvent, the protein in solvent, and the protein-ligand complex in solvent and subtracting the mean energies, while ensuring that the composition of the bound state systems is identical to that of the unbound state systems; for example, the number of water molecules must match exactly between the bound and free states. Here, however, we computed the relative binding free energies of a series of similar ligands (with the same protein). This avoids the requirement of converging the mean energy of the free protein, which might be particularly difficult due to possible conformational shifts on removal of ligands from the binding site. The relative binding enthalpies considered in this study were computed according to the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
Here ⟨UL,aX⟩ is the mean potential energy of a simulation of solvent with ligand aX, where a is c or f, indicating a constrained or flexible peptide, respectively, and X is V or Q, indicating that the second residue is valine or glutamine, respectively—such that fV refers to ligand fpYVN. The potential energies for simulations of the corresponding protein-ligand complexes are given analogously as ⟨UPL,aX⟩. Equations (1) and (2) report the energetic consequences of going from the flexible to the covalently constrained ligands, while Eqs. (3) and (4) report the energetic consequences of going from a central valine residue to a glutamine, for either the constrained or flexible case. In order to obtain correctly balanced energies, the numbers and protonation states of waters, ions, and buffer compounds were identical across all simulations, except for the addition of counterions required to maintain electrical neutrality, and their contributions cancel in the final results; simulation details are provided in Sec. II B.
Because the force field is additive, these relative binding enthalpies can be decomposed into contributions from structural components. For example, one contribution to the relative binding enthalpy of two ligands is the difference in their change in internal energy on binding. This can be computed by a post-analysis of each simulation that isolates the ligand and computes its mean internal energy.
B. Molecular dynamics simulations
Each of the four ligands was simulated in complex with the Grb2 SH2 domain, and free in solution (i.e., without protein). The structures of these ligands in complex with the Grb2 SH2 domain have been solved11 and are available in the Research Collaboratory for Structural Biology Protein Data Bank (RSCB PDB):29 fpYVN (3C7I) and cpYVN (2HUW); fpYQN (3IMD) and cpYQN (3IN7). The starting coordinates of the complexes were prepared from their respective crystal structures, using Maestro;30 crystallographic waters within 5 Å of the ligand were retained; and missing hydrogens were added. For the free ligand simulations, the coordinates of the ligand alone were extracted from the crystal structure and used as a starting point.
The complexes and free ligands were then solvated with TIP3P water, buffer molecules, and ions to approximate the experimental conditions.11 To facilitate the calculation of relative binding enthalpies, the contents of each simulation box were kept identical, except for the choice of ligand, whether or not the protein was present, and the requirement for additional sodium ions to ensure electrical neutrality of the overall system (see below). Thus, each truncated octahedral simulation box, measuring 12 Å from the solute to the box edge for the complex and 23 Å for the free ligand, was populated with 6034 TIP3P31 waters, 6 HEPES molecules, and 17 NaCl to approximate the 50 mM HEPES and 150 mM NaCl solution used in the isothermal titration calorimetry (ITC) experiments.11 To match the pH 7.45 conditions of the experiments, the charges on the residues of Grb2 SH2, including the protonation states of the histidines, were determined with the H++ 3.0 server (http://biophysics.cs.vt.edu).32–34 Based on the pKa values predicted by MarvinSketch 14.10.7.0, 2014, ChemAxon (http://www.chemaxon.com), three different ionization states of HEPES were included (see the supplementary material). At pH 7.45, the total charges of the Grb2 SH2 protein, the 6 HEPES molecules, and each ligand are +3, −3, and −2, respectively. Thus, to neutralize the simulation systems, additional Na+ ions were added: 2 for the complex systems, and 5 for the ligand-only systems. In total, the simulated complex systems comprised approximately 20 050 atoms, while the free ligand systems comprised approximately 18 400 atoms; the Grb2 SH2 domain has 1653 atoms.
Force field parameters were assigned to the protein, ligands, and buffer molecules with the LEaP program. The ff12SB force field35 was used for the protein, general AMBER force field (GAFF)36 force field parameters were used for HEPES, and force field parameters for the phosphotyrosine (PTY) residue were taken from the set determined by Steinbrecher et al.,37,38 as available in the AMBER frcmod.phosaa10 file. The cyclized phosphotyrosine (CPY) parameters were the same as PTY with the exception of the cyclopropyl moiety, which used the GAFF parameters for sp3 carbons in triangle systems (cx). Partial charges for both the HEPES molecules and the modified phosphotyrosine residues were determined using the restrained electrostatic potential (RESP) method, as available through the R.E.D. Server39,40 using Gaussian09 C.01.41 The full set of parameters used is available in the supplementary material.
The MD simulations were performed with the multiple-GPU version of PMEMD (pmemd.cuda.MPI).26 The systems were NVT heated to 300 K and NPT equilibrated for 5 ns, and the resulting equilibrated coordinates were used as the initial coordinates for the production simulations. The simulations were performed using periodic boundary conditions, with a nonbonded cutoff of 9 Å. The SHAKE algorithm was used to constrain the lengths of bonds involving hydrogen atoms. Pressure and temperature were regulated by using a Monte Carlo barostat26 and a Langevin thermostat, respectively. Hydrogen mass repartitioning was enabled, to allow the use of a long (4 fs) time step.27 A prior study showed that this approach does not lead to significant differences in computed binding enthalpies.23 The simulations were run in 200 ns blocks, with each block seeded by a new random number. Coordinates and energies were recorded every 500 steps (2 ps).
For each system, two replicate simulations, termed Run A and Run B, were initiated using the same equilibrated starting coordinates, but different random number seeds. Each replicate was simulated for 20 μs for the free ligands and over 125 μs for the complexes so that the total simulation time was 40 μs for each free ligand and over 250 μs for each complex; see Table IV for details.
TABLE IV.
Mean potential energies ⟨U⟩ and their SEMs (σ) (kcal/mol). Simulation duration t given in μs. SEM values are estimated based on statistical inefficiency.
| Complex | Free ligand | ||||||
|---|---|---|---|---|---|---|---|
| Ligand | Run | t | ⟨UPL⟩ | SEM σ | t | ⟨UL⟩ | SEM σ |
| fV | A | 166 | −64 126.7 | 0.87 | 20 | −61 938.3 | 0.06 |
| B | 169 | −64 131.4 | 3.03 | 20 | −61 938.5 | 0.06 | |
| cV | A | 128 | −64 155.7 | 0.78 | 20 | −61 971.9 | 0.06 |
| B | 141 | −64 158.4 | 1.49 | 20 | −61 971.8 | 0.06 | |
| fQ | A | 127 | −64 178.7 | 0.54 | 20 | −61 986.0 | 0.06 |
| B | 127 | −64 176.7 | 0.43 | 20 | −61 985.6 | 0.06 | |
| cQ | A | 133 | −64 207.4 | 1.08 | 20 | −62 019.2 | 0.06 |
| B | 133 | −64 212.1 | 1.62 | 20 | −62 019.2 | 0.06 | |
C. Evaluation of uncertainty
In addition to the use of non-identical replicate calculations (Sec. II B), we used two different methods, previously detailed in Henriksen et al.,23 to estimate uncertainties based on the individual trajectories. Using the approach described by Shirts and Chodera,42 the statistical inefficiency is determined from the autocorrelation function of the energy to create a subsampled data series that is uncorrelated, at least in principle. The standard error of the mean (SEM, σ) is then computed for the resulting uncorrelated series. Blocking analysis43 is another approach to estimating the uncertainty of the time series of potential energies, where block-wise SEMs are computed for successively longer blocks of energies. On a plot of SEM vs. block size, a plateau is generally seen for simulations that are considered converged, and the SEM value corresponding to the plateau is taken as the error of the estimation. However, we have observed that, especially when a clear plateau is absent, a more conservative (i.e., larger), and more reliable error estimate is the largest SEM reached for any of the block sizes tested,23 so we use the latter metric.
D. Principal component analysis
To look for large-scale, slow protein motions that might account for slow convergence of the mean energy in a simulation, we applied principal component analysis (PCA) to the simulated trajectories of the complexes and free ligands. PCA is commonly used to determine the essential dynamics of a simulation44,45 by reducing the dimensionality of the trajectory motions. Principle components, or PCs, are the eigenvectors obtained from diagonalizing the covariance matrix of a trajectory, and the eigenvector with the largest eigenvalue is the linear combination of Cartesian coordinates that captures the most variance. We used the cpptraj program to obtain the first three PCs for concatenated trajectories of the simulation replicates for each system (Run A and Run B) and then to project the individual trajectories onto each PC. All atoms of the ligands and just the Cα atoms of the proteins were included in these analyses.
E. Structural decomposition of relative binding enthalpies
We sought insight into the computed relative binding enthalpies by isolating the mean energies associated with parts of the overall system, notably the ligand and a set of residues that form the binding site. We focused on the binding site based on an expectation, on physical grounds, that this will be the region with the largest differences across ligands, and because limiting attention to this smaller region reduces numerical noise in the component analysis. To generate ligand-only trajectories, we used cpptraj26 to delete the protein and all solvent molecules, including water, HEPES buffer, and ions, from each trajectory. We similarly generated trajectories containing only 13 binding site residues (Arg13, Arg32, Ser34, Glu35, Ser36, Ser42, Val51, Gln52, His53, Phe54, Lys55, Leu66, and Trp67), with and without the bound ligand; the rest of the protein and all solvent molecules were stripped. The potential energies of the decomposed systems were then evaluated by specifying imin = 5 and maxcyc = 1 in the sander26 program to read in the trajectories and calculate a single-point energy at each frame. PME was disabled by using ntb = 0 so that no periodicity was applied and long-ranged interactions were accounted for instead by increasing the nonbonded cutoff to 100.0 Å.
To define the energy components computed here, we introduce the following notations:
-
•
: mean internal energy of protein binding site residues and ligand i, in their bound complex;
-
•
: mean internal energy of protein binding site residues only, from simulation of bound complex with ligand i;
-
•
: mean internal energy of ligand i only, from simulation of its bound complex with protein;
-
•
: mean internal energy of ligand i only, from simulation free in solution.
Then the mean interaction energy of ligand i and binding-site residues from the simulation of their bound complex is
| (5) |
The change in the internal energy of ligand i on binding is
| (6) |
The difference between the binding site internal energy when ligand i is bound versus when ligand j is bound is
| (7) |
F. Changes in first-order configurational entropy
We estimated changes in configurational entropy of the ligands and binding-site residues, to further study the consequences of ligand preorganization. The configurational entropy, S, may be written as an expansion in terms of first-order terms, pairwise mutual informations, third-order mutual informations, and so forth.46–48 Here, we examine only the relatively tractable first-order term S(1), which provides a useful look at overall trends.48 The change in first-order entropy of ligand i on binding for dihedral angle n is obtained by binning the dihedral, ϕin, into m = 1…Nbins to create a normalized probability distribution and computing its first-order contribution to the binding entropy as
| (8) |
where Pm(ϕn) and are the probabilities in bin m for the free and bound states, respectively, and we have omitted the superscript (1) for simplicity. The total first-order binding entropy for ligand i is then calculated as the sum of the contributions from its Ndih dihedral angles
| (9) |
The relative binding entropy of ligands i and j then is ΔΔSij,bind = ΔSj,bind − ΔSi,bind.
One may also compare the absolute configurational entropies of two ligands, i and j, as
| (10) |
where subscripts i and j indicate the ligand associated with each probability distribution, the first equation pertains to the free state, and the second equation pertains to the bound state.
To compute the torsional entropies of the peptide ligands, we analyzed a minimal, non-redundant, set of rotatable torsions. Although an additional bond is present in the constrained ligands, we note that it does not introduce any new non-redundant torsions, so the constrained and flexible phosphotyrosines (cpY and fpY) were defined by the same minimal set of torsions. When computing such relative entropies comparing ligands containing glutamine versus valine, the additional glutamine-specific torsions were excluded, so equal numbers of degrees of freedom were considered. Analogous calculations yield the difference in entropy of torsions in the binding site residues, with ligand i versus j bound: ΔSB,ij. The rotatable torsions of the following binding site residues were analyzed: Arg13, Arg32, Ser34, Ser36, Ser42, His53, Phe54, and Lys55 which are a subset of the 13 residues used in the structural decomposition analysis (Sec. II E) that had native contacts of 4 Å or less for greater than half the simulation (see Sec. II G). In the following, we report entropies as free energy contributions of the form −TΔS, in units of kcal/mol, to facilitate comparison with energies. The dihedral angles used for these analyses are listed in the supplementary material. Histograms for the selected dihedrals were generated from the trajectories with cpptraj, using 180 bins of size 2°.
G. Native contact analysis
We used the nativecontacts program within cpptraj to determine, for each simulation of a protein-ligand complex, the fraction of time; the native protein-ligand contacts were maintained, in the sense of being shorter than 4.0 Å. This analysis tracked all protein-ligand interatomic distances that were ≤4.0 Å in the starting (crystal) structure of each simulation, omitting distances involving hydrogen atoms.
III. RESULTS
This section begins by comparing the computed and experimental relative binding enthalpies of the four ligands and by providing structural analyses that help explain the computational results. The four molecular recognition events are then further characterized in terms of changes in configurational entropy and flexibility. Finally, we provide a detailed analysis of convergence and numerical precision of the mean potential energies that are used to characterize the enthalpies.
A. Analysis of relative binding enthalpies
One of the more intriguing experimental observations regarding this system is that the constrained peptides have more favorable binding enthalpies than their corresponding flexible peptides, by 1.1 and 2.5 kcal/mol,11 as listed in the first two rows of Table I. By contrast, the calculations assign both flexible peptides more favorable binding enthalpies, by 1.3 and 5.4 kcal/mol (ΔΔH in Table I), relative to their corresponding constrained peptides. This deviation between calculation and experiment holds across both peptide sequences. In addition, the differences are substantial on the scale of the experimental and computational uncertainties, particularly for cV and fV, where calculation deviates from experiment by nearly 8 kcal/mol.
TABLE I.
Experimental (ITC) and simulated relative binding enthalpies (ΔΔH), along with simulated binding site energy differences (ΔuB), relative ligand-protein interaction energies (ΔΔuinter), and relative changes in ligand internal energy on binding (ΔΔuL) for each ligand pair. Computations are based on the combined (concatenated) parallel runs for each system (Runs A and B). The relative difference in all remaining terms is also reported, as ΔΔuother; see main text. The standard errors of the mean (SEM) (σ) are propagated from those estimated using the statistical inefficiency applied to combined runs. The experimental errors are taken from Ref. 11, which are propagated from the errors in ligand concentration. Units: kcal/mol.
| Expt.11 | Simulated | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITC | Err | ΔΔH | σ | ΔΔuinter | σ | ΔuB | σ | ΔΔuL | σ | ΔΔuother | σ | |
| cV–fV | −2.5 | 0.32 | 5.38 | 2.11 | 24.73 | 6.12 | 10.00 | 2.68 | −4.83 | 1.05 | −24.5 | 7.01 |
| cQ–fQ | −1.1 | 0.30 | 1.33 | 1.25 | 22.03 | 4.34 | 4.12 | 2.06 | 0.66 | 1.85 | −25.5 | 5.01 |
| fQ–fV | −3.3 | 0.27 | −1.19 | 1.87 | 0.76 | 4.68 | −1.27 | 1.54 | −5.54 | 1.39 | 4.86 | 5.27 |
| cQ–cV | −1.9 | 0.35 | −5.24 | 1.59 | −1.94 | 5.87 | −7.15 | 3.01 | −0.04 | 1.61 | 3.89 | 6.95 |
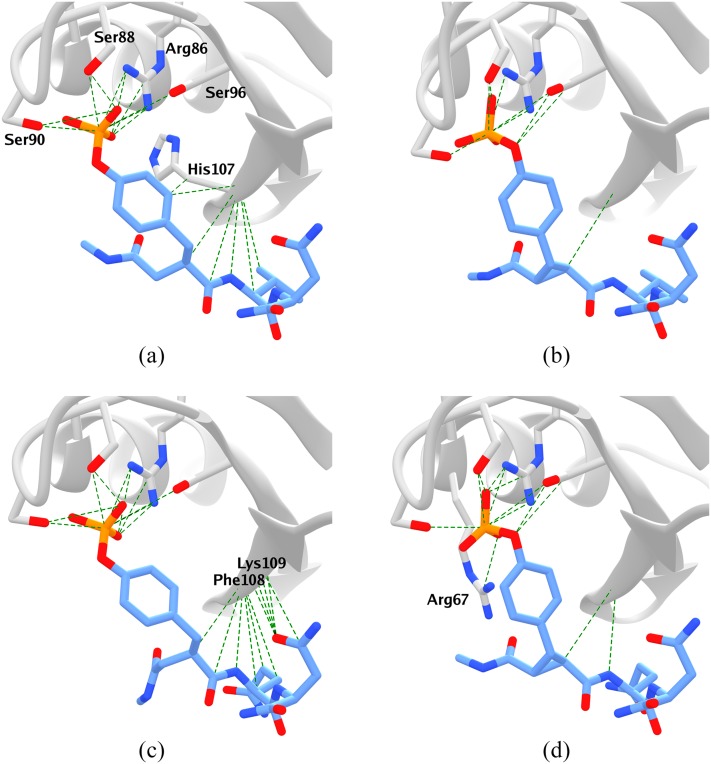
The fact that the flexible ligands bind more favorably in these calculations traces in part to the fact that they make more favorable contacts with the protein binding site, by over 20 kcal/mol, as evident from the values of ΔΔuinter in Table I. In addition, the internal energy of the binding site is more favorable when the flexible ligands are bound, relative to the constrained ligands, as evident from the values of ΔuB in Table I. Presumably, the flexible ligands can form more intimate interactions and also allow the binding site to adopt a more relaxed conformational ensemble, compared with the more rigid constrained ones. Indeed, the flexible ligands maintain their crystallographic interactions with the binding site during more of the simulations than do the constrained ligands. This is shown in Fig. 2, which depicts the native contacts present for greater than 50% of each complex simulation. The flexible ligands maintain multiple native contacts [Figs. 2(a) and 2(c)], with many formed between the central residue of the ligand (Val or Glu) and the protein backbone (His107, Phe108, and Lys109); the corresponding contacts are poorly maintained by the constrained ligands [Figs. 2(b) and 2(d)].
FIG. 2.
Native contacts (distance ≤ 4.0 Å in the crystal structure) that are present in at least half of the snapshots of the combined Run A and Run B simulations of each protein-ligand complex. (a) fV, (b) cV, (c) fQ, and (d) cQ.
By contrast, the corresponding crystal structures tend to show more favorable polar contacts between the constrained peptides and the protein, relative to the flexible ones.11 This observation is broadly consistent with the fact that the experiments assign more favorable binding enthalpies to the constrained peptides, while the calculations show the opposite pattern. It is also worth keeping in mind, when making detailed comparisons among the four crystal structures, that they were solved in four rather different solvents and represent three different space groups (Table II).
TABLE II.
Crystallization conditions and crystal properties for the protein-ligand complexes simulated here.
| fV | cV | fQ | cQ | |
|---|---|---|---|---|
| pH | 5.0 | 6.0 | 8.5 | 7.5 |
| Solvent | Formate | Cacodylate, PEG | HEPES, PEG | MgCl2, TRIS, PEG |
| Resolution (Å) | 1.7 | 1.9 | 2.0 | 2.0 |
| Space group | P 43 21 2 | P 1 21 1 | P 21 21 21 | P 21 21 21 |
| T (K) | 100 | 100 | 100 | 100 |
| Mean B (Å2) | 20 | 25 | 11 | 32 |
| Solvent content (%) | 30 | 40 | 31 | 43 |
Subtracting the component energies, ΔΔuinter, ΔuB, and ΔΔuL, from the relative binding enthalpies, ΔΔH, yields ΔΔuother, the contribution of the solvent and the remainder of the protein, which includes their interactions with the ligand and binding site, to the overall relative binding enthalpies. This “other” contribution strongly favors binding of the constrained ligands (Table I), and, indeed, nearly cancels the contributions of the other components. Intuitively, the formation of favorable interactions between the ligands and the binding site, and within the binding site, is largely balanced by losses in favorable interactions involving the solvent and the rest of the protein.
The present calculations do replicate the experimental trend that the glutamine-containing peptides, fQ and cQ, have more favorable binding enthalpies than their valine-containing counterparts, fV and cV. Here, since the computed relative binding enthalpies are within 5.2 kcal/mol of zero, the uncertainties of up to about 2 kcal/mol in the calculations (above) are more problematic. However, the consistency of the results between both pairs of peptides supports the solidity of the conclusion. The more favorable binding enthalpy of the glutamine-containing peptides does not correlate clearly with stronger ligand-protein interactions (Δuinter, Table I), although this might have been expected given the ability of the Q residue to hydrogen-bond with the protein. The absence of hydrogen bonds between the ligand glutamines and the protein is consistent with the crystal structures. Instead, the binding site itself adopts somewhat lower energy conformations in the presence of fQ and cQ, versus fV and cV, as evident from the positive values of ΔuB in Table I.
B. Changes in ligand configurational entropy on binding
We also examined changes in the configurational entropy of the ligands and the binding site. The first-order estimates used here, which are based on the probability distribution functions of rotatable bonds, quantify changes in thermal motion on binding. We checked the convergence of these calculations by computing the first-order entropies for subsets of frames from the total simulation and found that the final values were always within a standard deviation of the values estimated by the subsets (see Figs. 2 and 3 of the supplementary material).
Although it may be expected that a more rigid ligand will incur smaller losses in configurational entropy on binding, we see the opposite pattern: the constrained peptides lead to considerably more unfavorable changes in configurational entropy on binding than the flexible ones, by 7-8 kcal/mol, at least for the ligand and binding-site torsions considered here (Table III, Sum). This result is consistent with the paradoxical experimental observation that the entropy of binding is less favorable for the constrained than the flexible ligands. (Note, however, that the experimental entropies account for the entire system, including the solvent, whereas the present results account only for a small number of ligand and binding-site torsions.) That the constrained ligands lead to more unfavorable changes in configurational entropy on binding traces primarily to the binding site torsions, rather than the ligands themselves: binding of the constrained ligands leads to about a 5 kcal/mol greater loss of configurational entropy in the binding site than does binding of the flexible peptides (Table III, −TΔSB,ij). This is physically plausible because a more rigid ligand may constrain the binding site more, as previously suggested.11,49
TABLE III.
Differences in first-order contributions to the configurational binding entropy, for ligands only (−TΔΔSij,bind), for binding site residues only (−TΔSB,ij), and for ligand and binding site combined (Sum). Results are computed with the combined (concatenated) parallel runs for each system (Runs A and B), and are presented as free energy contributions, in kcal/mol.
| −TΔΔSij,bind | −TΔSB,ij | Sum | |
|---|---|---|---|
| cV–fV | 1.62 | 5.50 | 7.12 |
| cQ–fQ | 3.29 | 5.01 | 8.30 |
| fQ–fV | −1.64 | −0.25 | −1.89 |
| cQ–cV | 0.03 | −0.75 | −0.71 |
These computational results may appear inconsistent with the fact that the crystallographic B-factors run lower for the proteins solved with the flexible ligands than with the constrained ones (Table II) since B-factors are interpretable, in part, as indicators of atomic motion. However, our simulations pertain to the protein-ligand complexes in solution, rather than in their crystal forms, which introduce not only lattice contacts but also very different solvent conditions, so it is not clear how informative crystallographic B-factors are for the conditions used in the ITC experiments. Moreover, the B-factor differences here are not limited to the binding site region, but instead are quite uniform across the entire protein, so another factor may be in play. We conjecture that the B-factor differences result, at least in part, from differences in solvent content. It has previously been reported that the mean B-factor of a protein crystal correlates with the percent solvent content of the crystal, with a slope of about 1.35 Å2/percent solvent. This makes intuitive sense because greater solvent content would presumably reduce the degree to which the crystal lattice restrains the motions of protein atoms. Here, the two crystal structures with the flexible ligands have solvent contents about 10% greater, in absolute terms, than those solved with the constrained ligands (Table II), and this is the right order of magnitude to account for the observed B-factor differences.
The computed changes in ligand torsional entropy on binding also are more unfavorable for the constrained ligands than for the corresponding flexible ones (Table III, −TΔΔSij,bind). This result is consistent with the prior computational study of this system,50 which found that the flexible ligands form internal nonbonded interactions which reduce their conformational flexibility when free in solution; while these interactions did not form in the constrained peptides. We wished to compare the configurational entropies of the constrained and flexible ligands in solution, similarly, but a direct comparison cannot be made between ligands with different numbers of torsion angles. Therefore, we recomputed the configurational entropies of free fQ and cQ, this time omitting the χ2 and χ3 torsions of the glutamine, to generate entropy estimates based on 17 torsions that chemically match the 17 torsions of fV and cV [Eq. (10)]. Consistent with the prior study, we find that the constrained peptides have greater configurational entropy in solution than the flexible ones, by about 1 kcal/mol (see the supplementary material for details). However, the constrained peptides have less configurational entropy when they are in the binding site, by 0.6–1.5 kcal/mol (see the supplementary material), even though they have fewer stable native protein-ligand interactions than the flexible ligands (see above).
C. Precision, convergence, and slow protein motions
The numerical precision of mean potential energies from the simulations was examined by three different approaches: evaluation of statistical inefficiency through the time autocorrelation function of the potential energy;42 blocking analysis;43 and comparison of duplicate runs seeded with different random number (i.e., Runs A and B). The results are detailed in Subsections III C 1–III C 3.
1. Ligands free in solution
For the free ligands, both the autocorrelation and blocking analyses yield SEM estimates of <0.1 kcal/mol (Table IV), for both the individual and combined duplicate runs, A and B. In addition, the blocking curves show appropriate plateaus [panels (b) and (d) in Figs. 3 and 4], and the duplicate runs provide mean energies that deviate from their combined mean by 0.09 kcal/mol on average. (Mean potential energies and blocking graphs for the combined A and B runs are provided in the supplementary material.) Thus, the free ligand energies are well-converged by all measures, even for the individual 20 μs simulations.
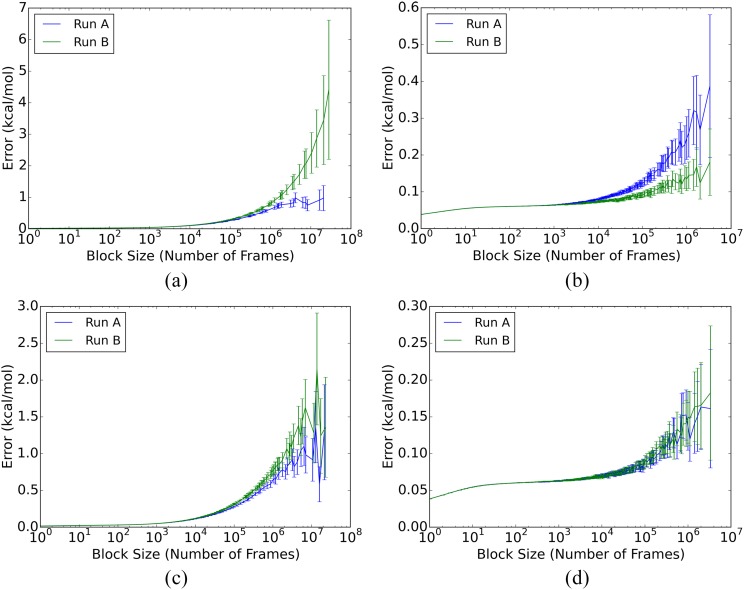
FIG. 3.
SEM blocking curves for fV and cV total potential energies. (a) fV, complex; (b) fV, free ligand; (c) cV, complex; and (d) cV, free ligand.
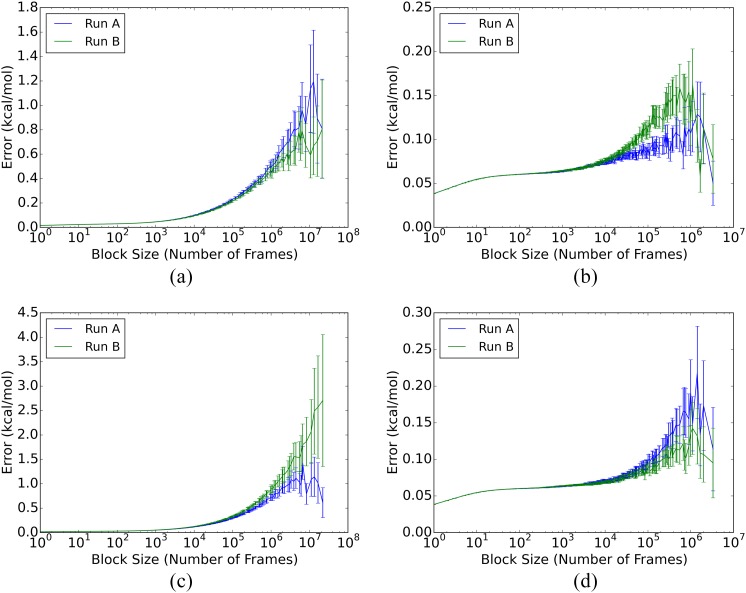
FIG. 4.
SEM blocking curves for fQ and cQ total potential energies. (a) fQ, complex; (b) fQ, free ligand; (c) cQ, complex; and (d) cQ, free ligand.
2. Protein-ligand complexes
The mean energies of the ligand-protein complexes converge relatively slowly, even on the scale of the present simulation times of over 250 μs for each complex, as detailed in Table IV. Thus, for the separate A and B runs, autocorrelation analysis yields SEM estimates of 0.4–3.0 kcal/mol, and none of the blocking curves of the individual runs show consistent plateaus [panels (a) and (c) in Figs. 3 and 4]. Additionally, the SEM estimates for the merged A and B runs range from 0.4 to 1.8 kcal/mol (Table 5 of the supplementary material), and blocking analysis of the merged runs still do not show consistent plateaus (Figs. 4 and 5 of the supplementary material). The uncertainties of these mean energies are about an order of magnitude greater than those for the free ligands, even though the simulations are nearly ten-fold longer.
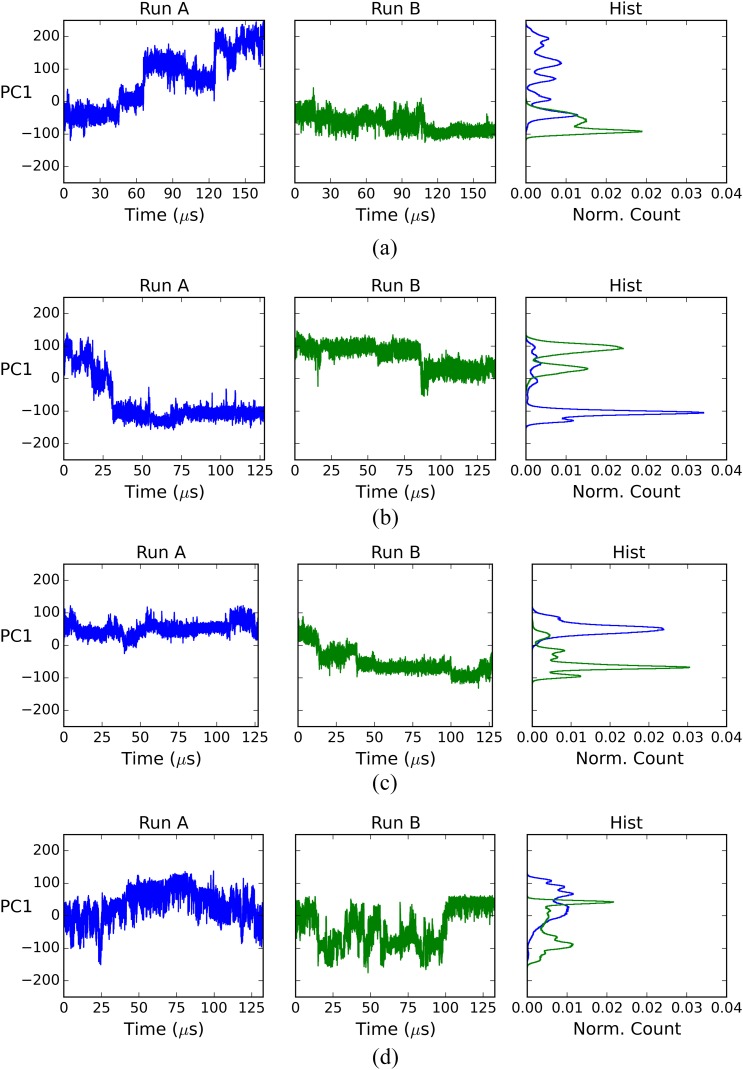
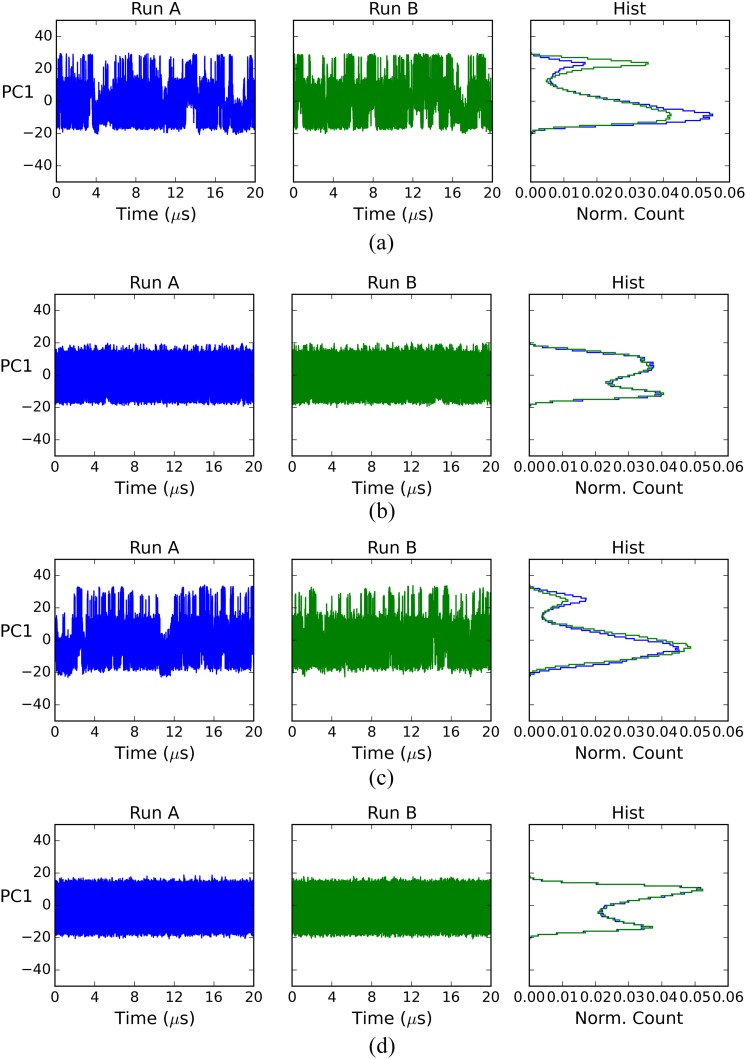
The slow convergence of the ligand-protein systems cannot be attributed simply to their size (∼20 000 atoms) because the free ligand systems (above) have a similar number of atoms (∼18 000), yet converge far more rapidly. We conjectured that slow motions of the protein in the complexes delay convergence by generating long correlation times not present in the free ligand simulations; we used principal component analysis (PCA) to test for such slow motions. For each complex and free ligand system, we combined the two replicate trajectories (runs A and B), computed the covariance matrix for the combined trajectory, and then projected each individual trajectory onto the combined trajectory’s first principal component (PC). This is the PC with the largest eigenvalue, which means that captures the greatest structural variance. Graphs of the resulting projections over time, and normalized histograms of these projections, are shown in Figs. 5 and 6.
FIG. 5.
First PC projection for complex simulations. (a) fV, complex; (b) cV, complex; (c) fQ, complex; and (d) cQ, complex.
FIG. 6.
First PC projection for free ligand simulations. (a) fV, ligand; (b) cV, ligand; (c) fQ, ligand; and (d) cQ, ligand.
The histograms for the complex simulations (the right column of Fig. 5) show that the two matched runs, A and B, sampled the leading PC differently. This result points to large-scale, slow motions as a possible factor in the slow convergence of the mean potential energies of the protein-ligand complexes. For the free ligands, by contrast, the Run A and Run B histograms overlap well (the right column of Fig. 6), indicating that the sampling along their leading PCs is similar between these two independent simulations. This result is consistent with the relatively facile convergence of the free ligand potential energies.
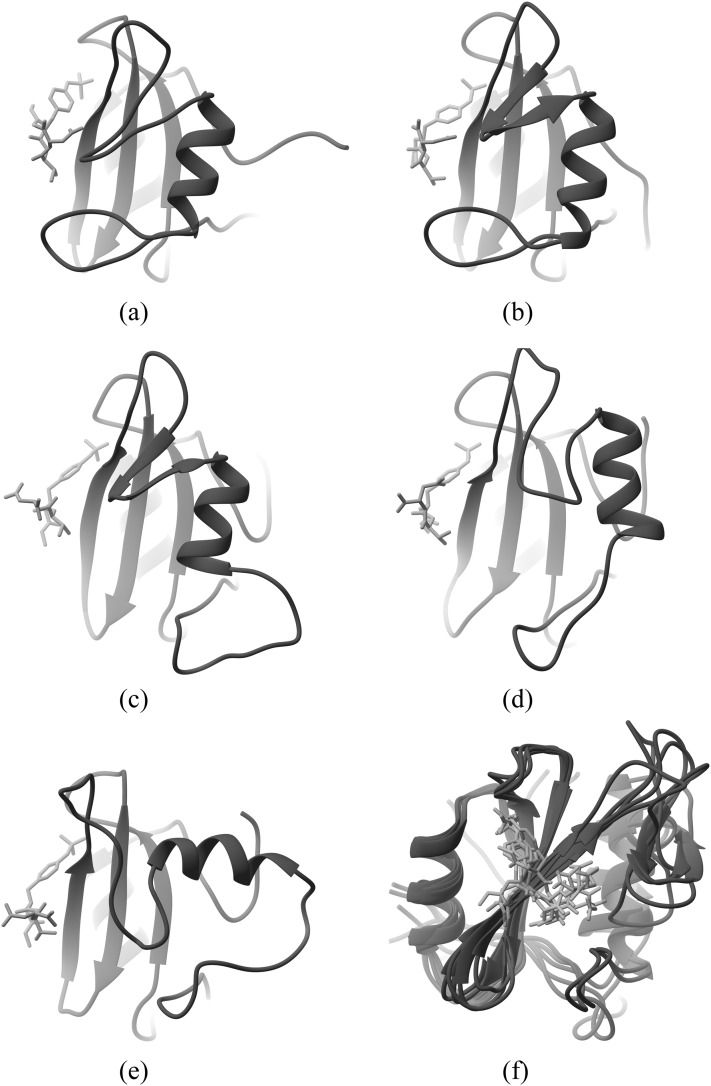
To better understand the slow motions of the protein in these complexes, we examined the structures at several time points of the simulations and observed that the conformation of the C-terminal loops and helix changes significantly during the simulations. An example is provided in Fig. 7, which depicts snapshots at 40 μs intervals [Figs. 7(a)–7(e)] during run A of the fV complex. This corresponds to the leftmost chart in Fig. 5(a). It is evident that the C-terminus gradually reconfigures from its initial, crystallographic conformation to a new conformation, in which the helix has rotated by about 90°. Despite this rearrangement of the C-terminal components of the protein, the rest of the protein, including the binding site region, maintains a stable structure. This may be seen more clearly in Fig. 7(f), which is an overlay of the structures of Figs. 7(a)–7(e), rotated so the binding site faces the viewer.
FIG. 7.
Snapshots of Grb2-SH2 complexed with the fV ligand, from the Run A simulation. (a) Crystal structure, (b) 40 μs, (c) 80 μs, (d) 120 μs, (e) 160 μs, and (f) overlay (binding site).
3. Component energies
We also examined the convergence of the mean potential energies of components of the simulated systems. For each complex simulation, we computed the mean internal energy of ligand i (Li), selected residues lining the binding site (B), and the combination of the ligand and the binding-site residues (BLi). For each free ligand simulation, we computed the mean internal energy of just the ligand (L). The uncertainties of these means, estimated by the same methods applied to the whole simulations (Table IV), are reported in Table V.
TABLE V.
Mean potential energies ⟨u⟩ and SEM σ for component structures (kcal/mol). BLi corresponds to the combination of the selected binding site residues and the bound ligand in complex, while B refers to the binding site residues alone and Li refers to the ligand alone. SEM values are based on statistical inefficiency for component energies.
| From complex simulations | From free ligand simulations | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ligand | Run | σ | σ | σ | σ | ||||
| fV | A | −407.2 | 5.54 | 170.9 | 0.74 | −54.7 | 0.45 | −61.7 | 1.09 |
| B | −393.3 | 4.01 | 174.1 | 1.57 | −56.5 | 1.06 | −61.4 | 0.59 | |
| cV | A | −390.4 | 5.54 | 186.4 | 2.94 | −93.6 | 0.60 | −93.7 | 0.11 |
| B | −413.6 | 5.68 | 179.0 | 2.78 | −92.0 | 0.50 | −94.0 | 0.16 | |
| fQ | A | −431.3 | 3.10 | 173.6 | 1.33 | −92.5 | 0.65 | −95.3 | 1.31 |
| B | −446.4 | 0.77 | 168.8 | 0.87 | −95.0 | 0.28 | −93.0 | 0.53 | |
| cQ | A | −444.7 | 4.60 | 178.9 | 2.68 | −123.9 | 0.74 | −125.7 | 0.05 |
| B | −442.5 | 3.16 | 171.8 | 1.92 | −125.5 | 2.93 | −125.7 | 0.05 | |
For the free ligand simulations, the uncertainties in the isolated ligand energies, , tend to be larger than those for the total potential energies of the corresponding full systems (Table IV), which also include the waters, ions, and buffer molecules. Consistent with these results, the curves from reblocking analysis (see the supplementary material) show no plateaus, except for the free cQ ligand, which also has low SEMs in Table V. Thus, the ligands’ internal energies converge more slowly than do the energies of the full ligand-solvent systems, even though the ligands represent only a tiny part of each full 18 000 atom system. Put differently, the variance of the ligand alone is greater than that of the full system energy. This implies that the ligand internal energy anticorrelates strongly with other energy components of the full system. Such anticorrelation is physically plausible; for example, if the ligand’s internal energy falls when the ligand makes an intramolecular H-bond, the ligand-solvent interaction energy will rise, due to the resulting loss of a ligand-solvent H-bond.
For the complex simulations, a similar pattern is seen for the mean energy of the combined binding site and ligand, , and of the binding site alone, , as these have larger SEMs in general than those of the full simulated systems (Table IV). Again, this points to anticorrelation of these energy components with other energy components present in the full systems. However, the mean energies of the isolated ligands (, ) appear better converged. It is of interest that the uncertainties of the binding site and ligand together () are greater than those of the binding site and ligand separately (, ). The difference likely traces to large fluctuations in the ligand-binding site interaction energies, Δuinter,i, which are not present in the internal energies of the separate binding site and ligand. Inspection of the trajectories shows that parts of the ligands sometimes detach from the binding site, and then reattach. Such motions would indeed lead to large changes in the ligand-binding site interaction energies, along with anticorrelated changes in the ligand’s and binding site’s interactions with the solvent.
IV. DISCUSSION
The present paper describes molecular dynamics simulations of an experimentally characterized system that probes the effects of ligand preorganization on ligand-protein binding thermodynamics.11 Subsections IV A–IV C consider the relationship of the calculations to the experimental data; the physical picture of binding thermodynamics afforded by the simulations; and the strengths, weaknesses, and prospects of this and other computational approaches to computing binding enthalpies.
A. Calculation versus experiment
According to the simulations, the flexible phosphopeptides have more favorable binding enthalpies than their less flexible, constrained analogs, in contrast to the experimental data. Although even longer simulations could be useful to further reduce numerical uncertainty, the convergence achieved here is good enough that the discrepancy relative to experiment appears to be robust. Assuming that setup issues, such as protonation states, have been correctly handled, this result suggests that replicating experimental results will require a more accurate force field. It is thus of interest that prior simulations of constrained and flexible phosphopeptides drawn from the same experimental study,11 but using the more detailed AMOEBA force field,51 successfully replicated the experimental trend that the constrained peptides bind with more favorable enthalpies than the flexible ones.50 Nonetheless, the prior AMOEBA results are not more accurate in absolute terms: the absolute deviations of the AMOEBA results from experiment, 7.8 and 2.1 kcal/mol for cpYVN-fpYVN and cpYIN-fpYIN, respectively, are essentially the same as those observed here for cpYVN-fpYVN and cpYQN-fpYQN, 7.9 and 2.4 kcal/mol, respectively. As a consequence, it is not clear that this comparison with experiment can be interpreted as supporting the accuracy of simulations with AMOEBA over the simpler force field used here. Another related set of prior studies examined analogous constrained vs flexible phosphopeptides, but focusing on the Src SH2 domain instead of Grb2 SH2, yielded results exactly opposite to ours. Thus, enthalpy calculations with the CHARMM27 force field,52 and using simulations shorter than those reported here, suggested that the flexible peptide had less favorable binding enthalpies,28 whereas the converse was observed experimentally.53
The challenge of getting the relative binding enthalpies right may stem in part from the fact that these quantities are a balance of large, opposing contributions from different structural components, such as the ligand-binding site interactions and the internal binding site energies, much as previously noted in the context of host-guest binding.22 Thus, the net, relative binding enthalpies may be sensitive to small shifts in these large, opposing energy components. That binding is a small balance of large components may be understood by recognizing that binding of a ligand leads to the formation of strong new ligand-protein interactions, as well as new solvent-solvent interactions made by displaced water molecules. These negative energy changes are at least partly balanced by positive contributions from the loss of favorable ligand-solvent and protein-solvent interactions. A related observation is that the variances of the overall energies are smaller than those of the component energies, even though the latter derive from far fewer atoms. This means that the energy fluctuations of the various components are strongly anticorrelated with each other, a phenomenon which may be understood based on similar reasoning.
Prior studies have examined the sensitivity of binding enthalpies to the choice of force field parameters.25,54 Interestingly, enthalpies seem to be more sensitive to force field details than are binding free energies. For example, binding free energy calculations for ∼40 cyclodextrin-guest systems, with 10 different force field and water model choices, yielded a range of root-mean-square error (RMSE) values, relative to experiment, of 0.85–1.80 kcal/mol, whereas the corresponding range of RMSE values for the binding enthalpies was 0.92–4.0 kcal/mol.25 We have also observed surprisingly strong sensitivity of host-guest binding enthalpies to the choice of water model.24 If it is in general true, as we suspect, that enthalpies are more sensitive to force field parameters than are free energies, this would represent a purely in silico case of entropy-enthalpy compensation.
B. Ligand flexibility, binding enthalpy, and configurational entropy
According to the simulations, the flexible ligands make much more energetically favorable interactions with the binding site than do the constrained ligands, by on the order of 20 kcal/mol. In addition, the binding site residues are predicted to adopt conformations with a lower mean internal energy in the presence of the flexible ligands than with the constrained ones, by 4-10 kcal/mol. The experimental measurements cannot, of course, provide this level of granular detail. However, it is plausible on physical grounds that more flexible ligands should conform better to the binding site, and also allow the binding site residues to spend more time in their own preferred conformations. Thus, one may speculate that these trends in the component energies are at least qualitatively valid, and that the deviation of the overall relative enthalpies from experiment stems from an imbalance of these contributions with the counterbalancing contributions from solvent and the rest of the protein, as suggested above. Unfortunately, there is no possibility to compare the component terms with results from the prior simulation study of these systems50 because it used a method which did not allow the enthalpy changes to be broken down by structural component.
Calorimetry studies of the present systems showed that preorganizing the ligands with a conformational constraint led to less favorable binding entropies.11 This result was characterized as paradoxical because preorganization is typically expected to reduce the entropic penalty for immobilizing a ligand in the binding site.11,49 The authors of the experimental paper noted that this paradox would be resolved if the constrained ligands reduced the motions of the binding site residues more than did the flexible ligands. The prior simulation study did not examine this hypothesis, but provided intriguing evidence for another explanation, namely, that the flexible ligands actually are more conformationally restricted in solution than the constrained ones, due to the formation of stabilizing nonbonded interactions that the constrained ligands do not access.50 The present results are consistent with both of these suggestions, as we observe a greater loss of configurational entropy in the binding site for the constrained than the flexible ligands, and we also see that the flexible ligands are less conformationally mobile when free in solution. However, it is the binding site differences that dominate here, with configurational entropy differences of about 5-5.5 kcal/mol, compared with 1.5-3.3 kcal/mol for the ligands. It should be kept in mind that both the prior and the present studies used approximate methods to estimate changes in configurational entropy and that neither study includes contributions from water nor the bulk of the protein. This is, to our knowledge, the first computational study to address the influence of ligand flexibility on the configurational entropy of the binding site.
C. Computational methodology
In the present study, we used the direct approach to computing relative binding enthalpies. This involves simply taking differences between the average energies of free and bound states of the systems.21,22,28 A number of other approaches to computing binding enthalpies have been described,55–57 of which perhaps the most common is to compute binding free energies at several different temperatures, and then use in effect the van’t Hoff equation to extract the binding enthalpy at a temperature of interest. The potential benefit of the van’t Hoff approach is that, because the binding free energy is largely determined by the parts of the simulation system that interact at short range with the ligand, it may scale better with system size than the direct method, which requires converging the energy of the entire system, with all of its complex interactions. On the other hand, it is not trivial to obtain temperature-dependent binding free energies that are numerically precise enough to yield numerically precise binding enthalpies, and in fact, the direct approach was found to be considerably more efficient for host-guest binding systems.22 Another advantage of the direct approach is that, unlike the van’t Hoff approach, it allows an informative decomposition of the computed binding enthalpy by system components, as done here, and by energy terms, as done previously.22 It is also simpler to set up and run a direct enthalpy calculation than a series of binding free energy calculations at multiple temperatures.
Although we did not compare the direct and van’t Hoff approaches for the present systems, it is clear that the direct calculations were slow to converge by current standards, as simulations of over 250 μs duration still left us with uncertainties of 2-3 kcal/mol. Interestingly, though, the uncertainties were only this large for the protein-ligand systems. For the ligands alone, the convergence was excellent, even though the number of atoms in the free ligand systems was about the same as that in the protein-ligand systems. Thus, the problem was not the size of the protein-ligand systems, but the occurrence of slow conformational changes, involving drift of the C-terminal part of the protein away from its crystallographic conformation. This drift away from the crystal structure might reflect a problem with the force field. However, examination of the crystal structures reveals another possible explanation, the existence of crystal contacts that involve the C-terminus and that might have stabilized a crystallographic conformation that becomes unstable in solution. There may well be other proteins of similar size, or even larger, where such slow motions away from the crystal structure do not occur, and for which convergence of the direct method would, as a consequence, be substantially faster. Continued increases in computational speed, afforded by coprocessors like GPUs,58 and specialized computers like Anton 2,59 may well allow calculations like these to be converged to within 1 kcal/mol uncertainty within the next few years.
SUPPLEMENTARY MATERIAL
See supplementary material for 1—ionization states of HEPES buffer in the simulations; 2—list of peptide and binding-site torsion angles used in the entropy calculations; 3—graphs showing convergence of entropy estimates with simulation length; 4—details of ligand configuration entropies; 5—mean potential energies and uncertainties of Run A and Run B for each system; 6—blocking analysis graphs for concatenations of Run A and Run B for each simulation; and 7—mean potential energies and uncertainties of system components (e.g., ligand, binding site) for concatenated Runs A and B.
ACKNOWLEDGMENTS
We thank Niel Henriksen for valuable discussions and computational methods, particularly pertaining to the assessment of convergence and the dihedral angle analyses. This work was supported in part by the National Institute of General Medical Sciences, National Institutes of Health (NIH; Grant No. GM061300). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of the NIH. M.K.G. has an equity interest in, and is a cofounder and scientific advisor of, VeraChem LLC.
Contributor Information
Amanda Li, Email: .
Michael K. Gilson, Email: .
REFERENCES
- 1.Freire E., “A thermodynamic approach to the affinity optimization of drug candidates,” Chem. Biol. Drug Des. 74(5), 468–472 (2009). 10.1111/j.1747-0285.2009.00880.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ladbury J. E., “Isothermal titration calorimetry: Application to structure-based drug design,” Thermochim. Acta 380(2), 209–215 (2001). 10.1016/s0040-6031(01)00674-8 [DOI] [Google Scholar]
- 3.Prokopczyk I. M., Ribeiro J. F. R., Sartori G. R., Sesti-Costa R., Silva J. S., Freitas R. F., Leitão A., and Montanari C. A., “Integration of methods in cheminformatics and biocalorimetry for the design of trypanosomatid enzyme inhibitors,” Future Med. Chem. 6(1), 17–33 (2014). 10.4155/fmc.13.185 [DOI] [PubMed] [Google Scholar]
- 4.Chaires J. B., “Calorimetry and thermodynamics in drug design,” Annu. Rev. Biophys. 37(1), 135–151 (2008). 10.1146/annurev.biophys.36.040306.132812 [DOI] [PubMed] [Google Scholar]
- 5.Ward W. H. J. and Holdgate G. A., “Isothermal titration calorimetry in drug discovery,” in Progress in Medicinal Chemistry (Elsevier, 2001), Chap. 7, pp. 309–376. [DOI] [PubMed] [Google Scholar]
- 6.Garbett N. C. and Chaires J. B., “Thermodynamic studies for drug design and screening,” Expert Opin. Drug Discovery 7(4), 299–314 (2012). 10.1517/17460441.2012.666235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Falconer R. J., “Applications of isothermal titration calorimetry - the research and technical developments from 2011 to 2015,” J. Mol. Recognit. 29(10), 504–515 (2016). 10.1002/jmr.2550 [DOI] [PubMed] [Google Scholar]
- 8.Freire E., “Do enthalpy and entropy distinguish first in class from best in class?,” Drug Discovery Today 13(19), 869–874 (2008). 10.1016/j.drudis.2008.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ladbury J. E., Klebe G., and Freire E., “Adding calorimetric data to decision making in lead discovery: A hot tip,” Nat. Rev. Drug Discovery 9(1), 23–27 (2009). 10.1038/nrd3054 [DOI] [PubMed] [Google Scholar]
- 10.Fenley A. T., Muddana H. S., and Gilson M. K., “Entropy-enthalpy transduction caused by conformational shifts can obscure the forces driving protein-ligand binding,” Proc. Natl. Acad. Sci. 109(49), 20006–20011 (2012). 10.1073/pnas.1213180109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.DeLorbe J. E., Clements J. H., Teresk M. G., Benfield A. P., Plake H. R., Millspaugh L. E., and Martin S. F., “Thermodynamic and structural effects of conformational constraints in protein-ligand interactions. Entropic paradoxy associated with ligand preorganization,” J. Am. Chem. Soc. 131(46), 16758–16770 (2009). 10.1021/ja904698q [DOI] [PubMed] [Google Scholar]
- 12.DeLorbe J. E., Clements J. H., Whiddon B. B., and Martin S. F., “Thermodynamic and structural effects of macrocyclic constraints in protein-ligand interactions,” ACS Med. Chem. Lett. 1(8), 448–452 (2010). 10.1021/ml100142y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gomika Udugamasooriya D. and Spaller M. R., “Conformational constraint in protein ligand design and the inconsistency of binding entropy,” Biopolymers 89(8), 653–667 (2008). 10.1002/bip.20983 [DOI] [PubMed] [Google Scholar]
- 14.McNemar C., Snow M. E., Windsor W. T., Prongay A., Mui P., Zhang R., Durkin J., Le H. V., and Weber P. C., “Thermodynamic and structural analysis of phosphotyrosine polypeptide binding to Grb2-SH2,” Biochemistry 36(33), 10006–10014 (1997). 10.1021/bi9704360 [DOI] [PubMed] [Google Scholar]
- 15.De Vivo M., Masetti M., Bottegoni G., and Cavalli A., “Role of molecular dynamics and related methods in drug discovery,” J. Med. Chem. 59(9), 4035–4061 (2016). 10.1021/acs.jmedchem.5b01684 [DOI] [PubMed] [Google Scholar]
- 16.Borhani D. W. and Shaw D. E., “The future of molecular dynamics simulations in drug discovery,” J. Comput.-Aided Mol. Des. 26(1), 15–26 (2011). 10.1007/s10822-011-9517-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Durrant J. D. and McCammon J. A., “Molecular dynamics simulations and drug discovery,” BMC Biol. 9(1), 71 (2011). 10.1186/1741-7007-9-71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Śledź P. and Caflisch A., “Protein structure-based drug design: From docking to molecular dynamics,” Curr. Opin. Struct. Biol. 48, 93–102 (2018). 10.1016/j.sbi.2017.10.010 [DOI] [PubMed] [Google Scholar]
- 19.Abel R., Wang L., Harder E. D., Berne B. J., and Friesner R. A., “Advancing drug discovery through enhanced free energy calculations,” Acc. Chem. Res. 50(7), 1625–1632 (2017). 10.1021/acs.accounts.7b00083 [DOI] [PubMed] [Google Scholar]
- 20.Jorgensen W. L., “Efficient drug lead discovery and optimization,” Acc. Chem. Res. 42(6), 724–733 (2009). 10.1021/ar800236t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sellner B., Zifferer G., Kornherr A., Krois D., and Brinker U. H., “Molecular dynamics simulations of β-cyclodextrin-aziadamantane complexes in water,” J. Phys. Chem. B 112(3), 710–714 (2008). 10.1021/jp075493+ [DOI] [PubMed] [Google Scholar]
- 22.Fenley A. T., Henriksen N. M., Muddana H. S., and Gilson M. K., “Bridging calorimetry and simulation through precise calculations of cucurbituril-guest binding enthalpies,” J. Chem. Theory Comput. 10(9), 4069–4078 (2014). 10.1021/ct5004109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Henriksen N. M., Fenley A. T., and Gilson M. K., “Computational calorimetry: High-precision calculation of host-guest binding thermodynamics,” J. Chem. Theory Comput. 11(9), 4377–4394 (2015). 10.1021/acs.jctc.5b00405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gao K., Yin J., Henriksen N. M., Fenley A. T., and Gilson M. K., “Binding enthalpy calculations for a neutral host–guest pair yield widely divergent salt effects across water models,” J. Chem. Theory Comput. 11(10), 4555–4564 (2015). 10.1021/acs.jctc.5b00676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Henriksen N. M. and Gilson M. K., “Evaluating force field performance in thermodynamic calculations of cyclodextrin host–guest binding: Water models, partial charges, and host force field parameters,” J. Chem. Theory Comput. 13(9), 4253–4269 (2017). 10.1021/acs.jctc.7b00359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Case D. A., Babin V., Berryman J., Betz R. M., Cai Q., Cerutti D. S., Cheatham T. E. III, Darden T. A., Duke R. E., Gohlke H. et al. , Amber 14, 2014.
- 27.Hopkins C. W., Le Grand S., Walker R. C., and Roitberg A. E., “Long-time-step molecular dynamics through hydrogen mass repartitioning,” J. Chem. Theory Comput. 11(4), 1864–1874 (2015). 10.1021/ct5010406 [DOI] [PubMed] [Google Scholar]
- 28.Roy A., Hua D. P., Ward J. M., and Post C. B., “Relative binding enthalpies from molecular dynamics simulations using a direct method,” J. Chem. Theory Comput. 10(7), 2759–2768 (2014). 10.1021/ct500200n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Shindyalov I. N., and Bourne P. E., “The protein data bank,” Nucleic Acids Res. 28(1), 235–242 (2000). 10.1093/nar/28.1.235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schrödinger LLC, Schrödinger release 2014-2: Maestro, version 10.6, 2014.
- 31.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79(2), 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 32.Anandakrishnan R., Aguilar B., and Onufriev A. V., “H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations,” Nucleic Acids Res. 40(Web Server issue), W537–W541 (2012). 10.1093/nar/gks375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Myers J., Grothaus G., Narayanan S., and Onufriev A., “A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules,” Proteins: Struct., Funct., Bioinf. 63(4), 928–938 (2006). 10.1002/prot.20922 [DOI] [PubMed] [Google Scholar]
- 34.Gordon J. C., Myers J. B., Folta T., Shoja V., Heath L. S., and Onufriev A., “H++: A server for estimating pKas and adding missing hydrogens to macromolecules,” Nucleic Acids Res. 33(Web Server issue), W368–W371 (2005). 10.1093/nar/gki464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Case D. A., Darden T. A., Cheatham T. E. III, Simmerling C. L., Wang J., Duke R. E., Luo R., Walker R. C., Zhang W., Merz K. M. et al. , Amber 12, 2012.
- 36.Wang J., Wolf R. M., Caldwell J. W., Kollman P. A., and Case D. A., “Development and testing of a general amber force field,” J. Comput. Chem. 25(9), 1157–1174 (2004). 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- 37.Steinbrecher T., Latzer J., and Case D. A., “Revised AMBER parameters for bioorganic phosphates,” J. Chem. Theory Comput. 8(11), 4405–4412 (2012). 10.1021/ct300613v [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Homeyer N., Horn A. H. C., Lanig H., and Sticht H., “AMBER force-field parameters for phosphorylated amino acids in different protonation states: Phosphoserine, phosphothreonine, phosphotyrosine, and phosphohistidine,” J. Mol. Model. 12(3), 281–289 (2006). 10.1007/s00894-005-0028-4 [DOI] [PubMed] [Google Scholar]
- 39.Vanquelef E., Simon S., Marquant G., Garcia E., Klimerak G., Delepine J. C., Cieplak P., and Dupradeau F.-Y., “R.E.D. server: A web service for deriving RESP and ESP charges and building force field libraries for new molecules and molecular fragments,” Nucleic Acids Res. 39(suppl_2), W511–W517 (2011). 10.1093/nar/gkr288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dupradeau F.-Y., Pigache A., Zaffran T., Savineau C., Lelong R., Grivel N., Lelong D., Rosanski W., and Cieplak P., “The R.E.D. tools: Advances in RESP and ESP charge derivation and force field library building,” Phys. Chem. Chem. Phys. 12(28), 7821 (2010). 10.1039/c0cp00111b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., J. A. Montgomery, Jr., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J., and Fox D. J., gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2009. [Google Scholar]
- 42.Shirts M. R. and Chodera J. D., “Statistically optimal analysis of samples from multiple equilibrium states,” J. Chem. Phys. 129(12), 124105 (2008). 10.1063/1.2978177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Flyvbjerg H. and Petersen H. G., “Error estimates on averages of correlated data,” J. Chem. Phys. 91(1), 461 (1989). 10.1063/1.457480 [DOI] [Google Scholar]
- 44.Amadei A., Ceruso M. A., and Di Nola A., “On the convergence of the conformational coordinates basis set obtained by the essential dynamics analysis of proteins’ molecular dynamics simulations,” Proteins: Struct., Funct., Genet. 36(4), 419–424 (1999). [DOI] [PubMed] [Google Scholar]
- 45.Hayward S. and de Groot B. L., “Normal modes and essential dynamics,” Mol. Model. Proteins 443, 89–106 (2008). 10.1007/978-1-59745-177-2_5 [DOI] [PubMed] [Google Scholar]
- 46.Attard P., Jepps O. G., and Marčelja S., “Information content of signals using correlation function expansions of the entropy,” Phys. Rev. E 56(4), 4052 (1997). 10.1103/physreve.56.4052 [DOI] [Google Scholar]
- 47.Matsuda H., “Physical nature of higher-order mutual information: Intrinsic correlations and frustration,” Phys. Rev. E 62(3), 3096 (2000). 10.1103/physreve.62.3096 [DOI] [PubMed] [Google Scholar]
- 48.Killian B. J., Yundenfreund Kravitz J., and Gilson M. K., “Extraction of configurational entropy from molecular simulations via an expansion approximation,” J. Chem. Phys. 127(2), 024107 (2007). 10.1063/1.2746329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Martin S. F. and Clements J. H., “Correlating structure and energetics in protein-ligand interactions: Paradigms and paradoxes,” Annu. Rev. Biochem. 82, 267–293 (2013). 10.1146/annurev-biochem-060410-105819 [DOI] [PubMed] [Google Scholar]
- 50.Shi Y., Zhu C. Z., Martin S. F., and Ren P., “Probing the effect of conformational constraint on phosphorylated ligand binding to an SH2 domain using polarizable force field simulations,” J. Phys. Chem. B 116(5), 1716–1727 (2012). 10.1021/jp210265d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ponder J. W., Wu C., Ren P., Pande V. S., Chodera J. D., Schnieders M. J., Haque I., Mobley D. L., Lambrecht D. S., R. A. DiStasio, Jr. et al. , “Current status of the AMOEBA polarizable force field,” J. Phys. Chem. B 114(8), 2549–2564 (2010). 10.1021/jp910674d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mackerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., and Karplus M., “All-atom empirical potential for molecular modeling and dynamics studies of proteins,” J. Phys. Chem. B 102, 3586–3616 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- 53.Davidson J. P., Lubman O., Rose T., Waksman G., and Martin S. F., “Calorimetric and structural studies of 1,2,3-trisubstituted cyclopropanes as conformationally constrained peptide inhibitors of Src SH2 domain binding,” J. Am. Chem. Soc. 124(2), 205–215 (2002). 10.1021/ja011746f [DOI] [PubMed] [Google Scholar]
- 54.Yin J., Fenley A. T., Henriksen N. M., and Gilson M. K., “Toward improved force-field accuracy through sensitivity analysis of host-guest binding thermodynamics,” J. Phys. Chem. B 119(32), 10145–10155 (2015). 10.1021/acs.jpcb.5b04262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Levy R. M. and Gallicchio E., “Computer simulations with explicit solvent: Recent progress in the thermodynamic decomposition of free energies and in modeling electrostatic effects,” Annu. Rev. Phys. Chem. 49(1), 531–567 (1998). 10.1146/annurev.physchem.49.1.531 [DOI] [PubMed] [Google Scholar]
- 56.Lu N., Kofke D. A., and Woolf T. B., “Staging is more important than perturbation method for computation of enthalpy and entropy changes in complex systems,” J. Phys. Chem. B 107(23), 5598–5611 (2003). 10.1021/jp027627j [DOI] [Google Scholar]
- 57.Wyczalkowski M. A., Vitalis A., and Pappu R. V., “New estimators for calculating solvation entropy and enthalpy and comparative assessments of their accuracy and precision,” J. Phys. Chem. B 114(24), 8166–8180 (2010). 10.1021/jp103050u [DOI] [PubMed] [Google Scholar]
- 58.Xu D., Williamson M. J., and Walker R. C., “Advancements in molecular dynamics simulations of biomolecules on graphical processing units,” Annu. Rep. Comput. Chem. 6, 2–19 (2010). 10.1016/s1574-1400(10)06001-9 [DOI] [Google Scholar]
- 59.Shaw D. E., Grossman J. P., Bank J. A., Batson B., Adam Butts J., Chao J. C., Deneroff M. M., Dror R. O., Even A., Fenton C. H. et al. , “Anton 2: Raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer,” in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (IEEE Press, 2014), pp. 41–53. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for 1—ionization states of HEPES buffer in the simulations; 2—list of peptide and binding-site torsion angles used in the entropy calculations; 3—graphs showing convergence of entropy estimates with simulation length; 4—details of ligand configuration entropies; 5—mean potential energies and uncertainties of Run A and Run B for each system; 6—blocking analysis graphs for concatenations of Run A and Run B for each simulation; and 7—mean potential energies and uncertainties of system components (e.g., ligand, binding site) for concatenated Runs A and B.